Об одном решении задачи резонансных колебаний каната грузоподъемной установки с учетом его проскальзывания при навивке по поверхности барабана

Исследование динамики канатов переменной длины в рамках теории колебаний представляет значительный теоретический и практический интерес в задачах механики деформируемого твердого тела. Исторически разработка этих вопросов велась разрозненными группами, решавших задачи, которые на первый взгляд не имели между собой ничего общего. Так, специалисты по эксплуатации железных дорог и мостов изучали динамическую устойчивость конструкций под подвижными нагрузками, специалисты по силовым передачам — динамику гибких ветвей передач, а в горной механике — проблемы динамики шахтного подъема с использованием канатов переменной длины.

Широкое распространение в технике объектов с движущимися границами, от чувствительных элементов измерительных приборов и передач с гибкой связью до бурильных колонн и систем с упруго-инерционным основанием, обусловливает необходимость развития методов их математического моделирования. Особую актуальность эти задачи приобретают при разработке научных основ прочности, надежности и долговечности горных машин и механизмов [1 –3] , подъемно-транспортной [4, 5] , буксирной и траловой техники [6 –9] . В последнее время к этому перечню добавились задачи баллистики гибких нитей, увлекаемых движущимися телами, что открывает новые перспективы для приложений в специальных областях деятельности человека.

Математическая формулировка подобных задач выходит за рамки классических краевых задач математической физики и сводится к исследованию уравнений гиперболического типа в областях с переменными границами и интегро-дифференциальных уравнений с симметричными, зависящими от времени ядрами. Важным преимуществом интегральных методов является их эффективность при рассмотрении сложных динамических систем с сосредоточенными массами и подвижными нагрузками. Значительный вклад в развитие этой области внесли работы Х.А. Рахматулина [10] по изучению упруго-пластических волн в нитях, А.Н. Динника [11] по динамике шахтных подъемных канатов, А.С. Локшина [12] по расчету усилий в стержнях переменной длины.

В настоящее время для решения задач с подвижными границами применяются асимптотические методы Н.М. Крылова, Н.Н. Боголюбова и Ю.А. Митропольского [13] , метод Канторовича–Галеркина [14 –18] , а также метод построения решений интегро-дифференциальных уравнений [19 –21] . Однако до сих пор не существует общего подхода к формулировке этих задач, и в каждом конкретном случае требуется адаптация существующих методов.

Особую сложность вызывает математическое описание процессов, происходящих в системах с движущимися границами и неинтегрируемыми условиями связи. Классические подходы к моделированию подобных систем, предложенные в работах Н.П. Неронова [22] , Г.Н. Савина [23] , а также Г.Н. Савина и О.А. Горошко [24, 25] ,

Статья опубликована в открытом доступе по лицензии CC BY 4.0

сводятся к решению сложных функционально-дифференциальных уравнений, что существенно ограничивает возможности их анализа и практического использования.

В настоящей работе рассматривается задача о продольных колебаниях каната грузоподъемного устройства. Верхний конец каната наматывается на барабан, а нижний несет сосредоточенную массу груза; канат может скользить по поверхности барабана. Учет проскальзывания и движения границ принципиально меняет характер граничных условий: они становятся неголономными. Это приводит к необходимости разработки специальных математических методов изучения системы.

Основное внимание уделено интегральному подходу к формулировке задачи, позволяющему свести исходную проблему к интегро-дифференциальным уравнениям с симметричными ядрами. Благодаря этому открывается возможность применения асимптотических методов нелинейной механики и создания эффективных вычислительных алгоритмов для количественного анализа динамических характеристик системы. Предлагаемый подход и методы его реализации преодолевают ограничения классических подходов и представляют практическую ценность для расчета и оптимизации динамических показателей широкого класса грузоподъемных устройств и механизмов с переменной длиной несущих элементов.

• 2.    Постановка задачи

Рассмотрим задачу возникновения продольных колебаний каната грузоподъемной установки, наматываемого на барабан, а на нижнем (ненамотанном) конце, несущем жестко закрепленный груз [26] . За счет навивки на барабан, вращающийся с заданной скоростью, длина каната изменяется. Начало координат поместим в точке, в которой канат неподвижно связан с барабаном. Направление декартовой оси x совпадает с направлением действия силы тяжести.

Продольные колебания каната опишем уравнением:

Z_tt(x,t) - d 2 SgZ xx (x,t)= g.                                        (1)

В (1) обозначено: Z(x,t) — продольное смещение точки с координатой x в момент времени t; a = у/E/p — скорость распространения продольных колебаний , где E , ρ — модуль упругости и линейная плотность материала каната; S — площадь поперечного сечения каната; g — ускорение свободного падения. Здесь и далее индексы t и x указывают на дифференцирование функции Z(x,t) по соответствующему аргументу.

Граничное условие на нижнем — несущем, конце каната (x = l(t = 0)) представим как уравнение движения груза [26] :

Ztt(l(0),t) + ESgZx(l(0),t) = g.(2)

m

С учетом (1) граничное условие (2) принимает вид:

Zxx(l(0)^t) + aZx(l(0)^t) = 0.(3)

Здесь a = E/ mma²^ , m — масса груза.

В верхней точке (x = l ₀ (v ₀ t)) ненамотанной части каната при отсутствии проскальзывания граничное условие запишем так:

Zt(lo(vot),t) = F0‘ (^ot).(4)

Здесь l _o (v _o t) = L _o — v _o t — закон движения верхней границы, где v ₀ окружная линейная скорость точек поверхности барабана; L 0 —начальная длина каната; F _o (v _o t) —функция, характеризующая внешнее возмущение (штрих означает дифференцирование по времени); ω 0 — частота внешнего возмущения. Будем считать, что l _o (v _o t) является функцией медленного времени: т * = v _o t, l _o (v _o t) = 1 ₀ (т * ), то есть ее производная по времени dl o (v _o t)/dt = v ₀ dl ₀ (T)/dT * пропорциональна некоторому малому параметру v ₀ . На практике в подъемных установках условие медленного изменения параметров обычно соблюдается.

Проинтегрировав условие (4) по времени с учетом выражения для полной производной

Z t (l o (v o t) ,t) = dZ     ^’t ) — v o Z x (l o (v o t) ,t) 1 0 (v o t),                               (5)

получим:

t

Z (l o (v o t'),t') - v oj'Z x^v o Z ),Z)l o (v o Z)dZ = F o (^ o t).                             (6)

Граничное условие (6) — неголономное (неинтегрируемое). При фиксированной длине ненамотанного конца каната l' _o (v _o t) = 0 оно преобразуется к классическому виду:

Z (l o (v o t'),t') = FoM.

С учетом проскальзывания каната по поверхности барабана граничное условие в верхней точке ненамотанного конца становится следующим:

Z t (l o (v o t) — Al o (v o t) ,t) = F & (v o t),                                          (7)

где (l _o (v _o t) — Al o (v 0 t)) — положение точки, в которой исчезает проскальзывание каната при набегании на барабан. Разложим (7) в ряд Тейлора в окрестности точки x = 1 0 (v _o t) с сохранением только двух первых членов ряда:

Zt (lo (vot) ,t) — Alo (vot)Zxt (lo (vot) ,t) = F0 (^ot).(8)

Полный дифференциал функции Al _o (v _o t)Z _x (l _o (v _o t) ,t) с точностью до членов 2-го порядка малости имеет вид [26] :

d (Alo(vot)Zx(lo(vot),t)) = d (Alo(vot))Zx(lo(vot),t) + Alo(vot)Zxt(lo (vot),t).(9)

С учетом (8) и (9) из (7) следует:

Zt (lo (vot) ,t) = d- (Alo (vot)Zx(lo (vot) ,t)) — d- (Alo {vot))Zx (lo (vot) ,t) + F M.(10)

dtdt

Подставив (10) в (5) и проинтегрировав от 0 до t, получим граничное условие при наличии проскальзывания:

t

Z(lo№,t) — J‘Zx(lo(v0Z),Z)(l'o(voZ) — Al' Ы))dZ — Alo(vot)Zx(lo(vot),t) = Fo^t).(11)

о

Внешнее возмущение F _o (w_ot) в (11) примем равным

Fo(^ot)= vot+Asin(^ot), где Asin(^ot) — слабые возмущения гармонического характера, связанные с отклонением формы барабана от цилиндра, а также с его вибрациями .

Величины Al _o (v_ot), Al ’ (vot) нелинейно зависят от функций Z(l _o (v_ot),t), Z_x(l _o (vot),t). Максимальная длина дуги проскальзывания — Al max , наблюдается при скоростях вращения барабана v _o ^ 0. При этом проскальзывание отсутствует (AI = 0) при скоростях, больших некоторой критической скорости vq > v cr .

Для линеаризации (11) — граничного условия при наличии проскальзывания, введем усредненные оценки Al _o (vot), Al ’ (vot) величин Al _o (vot), Al ’ (vot):

π /2

4^.0=2

Al max cos(^vot) d(wv_Ot),

где ω — частота колебаний каната на основной динамической моде. Тогда

Al' ⁰ (vot) = — Al max ^v o sin(^v_ot).                                   (13)

С учетом (12) и (13) граничное условие (11) принимает линеаризованный вид:

t

Z (l o (v_ot),t)-l

Z x (l o (voZ),Z) ll'o(voZ) — Al 0 (v°Z )) dZ — Al o (v_ot)Z x (l o (v_ot),t)

= F o (^ot).

При фиксированной длине ненамотанной части каната l o = const граничное условие (14) становится следующим:

t

Z (lo,t) + Jz_x { Io,C ) Al 0 (voZ )dZ — Al o (v_ot)Z x (lo,t) = FoM.                      (15)

о

Условие (15) описывает проскальзывание каната по поверхности неподвижного барабана при колебаниях его ненамотанной части.

В случае, если скорость подъема v _o (t) переменная, между законом движения границы l _o (vot) и скоростью v _o (t) имеет место следующее соотношение:

l0 (vot)(1 + Zx(lo(vot),t)) = vo(t).(16)

При этом уравнение (1) и граничные условия (2) преобразуются к виду:

Ztt(x,t) —a2SgZxx(x,t)= g—v’ (t),(17)

Ztt (l(0),t)+ZZx(l(O),t) = g—v0 (t).

Знак минус в правой части (17) и (18) означает подъем груза.

Для определения длин ненамотанных концов канатов с высокой продольной жесткостью, например, стальных, после пренебрежения величиной Zx(lo(vot),t), малой по сравнению с единицей, вместо (16) можно пользоваться приближенной формулой:

t

l o

(v o t) = У v o (Z )dZ.

o

Таким образом, дифференциальное уравнение и линеаризованные граничные условия задачи о продольных колебаниях каната грузоподъемной установки, который наматывается на барабан, с учетом проскальзывания имеют вид (1) , (3) , (14) . При отсутствии проскальзывания в постановку задачи входит граничное условие в верхней точке ненамотанного конца каната (6) .

Начальные условия не влияют на резонансные свойства и принимаются следующими:

Z (E,0)=0,     Z t (E,0) = 0.

• 3.    Математическая модель продольных колебаний каната переменной длины

Применим метод построения решений интегро-дифференциальных уравнений [19 –21] при граничных условиях, содержащих неинтегрируемые члены, то есть в случае, когда длина ненамотанной части каната все время меняется. Тогда решение сводится к двойному интегрированию уравнения (1) в пределах l ₀ (v _o t) <  E <  l(0) с граничными условиями (3) , (14) .

Выполним первое интегрирование:

dZ (x,t) dZ (lo(vot),t)_ 1 X Г d2Z (s,t) dx         dx       a2Sg Jdt

l o ( v o t )

После повторного интегрирования (19) по x получим:

A                              dZ(lo(vot'),t')     1     [ ,     Г ^Z (St1.

Z(x,t)-Z(lo(vot),t)-\x-lo(vot)\-----dx-----= asg J  (x-s) —dt2g ds.(20)

l o ( v o t )

При построении выражения (20) использована методика изменения порядка интегрирования в двойном интеграле в правой части (19) . Уравнение (20) содержит искомую функцию и ее значения в граничных точках.

На основании (14) исключим из (20) граничное условие

t

Z (l o (v o t),t) = I

Z x (l o (v o Z ),Z ) (i o (v o Z ) - <  (v o Z )) dZ+Al o (v o t)Z x (l o Ы) ,t)+ F o (^ o t).

o

Для этого распространим интегрирование в (19) от l _o (v _o t) до l(0) и учтем граничные условия (2) :

dZ (loM,t ∂x

l(o)„ dZ (l(0),t)__1 Г   d2Z (s,t)

ds =

dx a2Sg Jdt lo(vot)

i (o)

m S' d ² Z (l(0),t)    \     1 Г Г d²Z (s,t)

ds.

ESg\   dt2     g) - a2Sg J [  dt2g lo(vot)

Подстановка (21) , (22) в (20) и запись результата преобразований относительно Z (x, t), приводит к интегро-дифференциальному уравнению:

t

Z(xA= /          do(voZ)-^(voZ)Х+лым'    .     -

∂x                                ∂xES

о

• (l(o)                      \X

m / д         \ р 7 Г d2Za jA? Г x- Гd - 1Л+Fo(4)t).(23)

g \    dt ²         / 9 J t dt ² J I g J es L dt ²

l 0 ( v 0 t )                                             l 0 ( v 0 t )

Используя свойство аддитивности, представим в (23) интеграл

l (0) !

как сумму:

x      l (0)

преобразований получим:

l o ( v o t )

I+

l 0 ( v 0 t )      ^x

. После элементарных

l (0)

у P f            ,_n[ ^d 2 Z(^s,t)   1.    ^{X - l}oM m ( ^{d 2} Z(l(O),t)   V

Z(x^ = -g J  K(x,s,lo(vot))[ —dt2g\dsES—— ---dt2g) + l0(v0t)

/dz(i _o (v _o z),z ) /, ‘,                             dZz(l o №,t)

+ ------ dx ------(l o tv o C^{) —} ^l o (v o ^z)' d^z+ ^Al o (v o ^t)-----dX +F o (^w o ^t).

В уравнении (24) ядро K(x,s,l _o (v _o t)) имеет вид:

{ s - l o (v o t)

ES x-lo(vot) ES

s ⩽ x, s ⩾ x.

Для каната переменной длины ядро является, с одной стороны, симметричной относительно x и s функцией влияния при фиксированном значении l _o (v _o t) = const, а с другой, — функцией, совпадающей с функцией удлинения каната. Кроме того, K(x,s,l _o (v _o t)), оставаясь симметричным, зависит от времени через параметр изменяющейся длины каната l _o (v _o t) .

Заметим, что существует альтернативный подход к построению решения задачи продольных колебаний каната переменной длины в виде интегро-дифференциального уравнения (24) . В качестве ядра для нового уравнения выберем функцию (25) , симметричную относительно своих аргументов x и s . Умножим уравнение (1) на K(x,s,l _o (v _o t)) и проинтегрируем по x в пределах от l _o (v _o t) до l(0):

l (o)                                                                         l (o)

P f          +\дd Z(s,t)  Ъ w f          Л\д2Z(sth g J K{x,s,lo{vot))l —dt2g]ds = ES J K(x,sMvot)) —7x2— ds.

l 0 ( v 0 t )                                                                           l 0 ( v 0 t )

Выполнив интегрирование по частям в правой части данного уравнения и приняв во внимание выражения (25) и граничные условия (2) и (14) , получим интегро-дифференциальное уравнение (24) .

Применим δ -функцию Дирака и обозначим:

p(x) = p+m6(x - l(0)).

Здесь p(x) — обобщенная функция распределения веса каната с сосредоточенным на конце грузом массой m. Уравнение (24) с учетом (26) становится следующим:

l (o)

Z(x^t) = - j l0 (v0 t)

p(s) Гd ² Z (s,t)

K ^(x,s,l o ^(v o t))— —--g g L    ot²

ds+

t

+ /            (io (voz)-Z(o (voz м ..,    .               Ft(27)

∂x∂x

При отсутствии проскальзывания (Al _o =0, Al ’ = 0) уравнение (27) преобразуется к виду:

l(0)t f"s>[ dZ (s^t            dZ (lo(voZ),Z)

^z{^x,t) = ^— j ^K(^x,s,l o (^vo^t))~g— —dt 2 ^{g ds+}j -----dX-----^l o (^vo^z)d^z+^F o {^ot).

l0(v0t)0

Введем в (27) новую функцию:

Z (x,t) = V (x,t) + Z (l o (v_ot),t) =

t

= V (x,t)+ f dz       ),z) (l' (voz)-Al’ (voz))dz+Alo№ "Z'    ' ,' ■ F - ,(28)

∂x∂x

где V(x,t) удовлетворяет граничному условию:

V (l o (v o t),t) = O.

Заметим, что —— ^{(    0 )} , ⁾ = ^^(-L),}. с учетом последнего после преобразований получим:

∂x∂x

t

Z(x,t)= V(x,t)+ d'V"'  (10(-oZ)-Al'oЫ)K+^lo(M"V ' ,' ' f ' •

∂x∂x

о

Подставив (28) и (29) в (27) и выразив V(x,t), придем к интегро-дифференциальному уравнению, описывающему колебания каната грузоподъемной установки с учетом проскальзывания:

i(o)2

d ( ^dV(loM,t) ,

⁺л(— d —lo^{(- o t)+}

V(x,t) = - / K(x,s,l o (- o ')) ^{p (} s ⁾ ^V ;^

J               g L dt lo(vot)

+Alo (— o ')

d2V (lo(-ot),t)A 1,

-----_я          ⁺ F o (^w o ^{t )} I^-g ds.

∂x∂t

Правая часть уравнения (30) имеет вполне определенный физический смысл. Слагаемые описывают: – влияние сил инерции ненамотанной части каната и груза на деформирование каната

l (0)

I ,             w P(s) d ² V (s,t)

• -    J к ⁽ x^,s^,l o ^{( -} o ^{t ))} — —— ds;

l 0 ( v 0 t )

– ограничения, налагаемые на скорость каната в точке навивки его на барабан

l (0)

• -    / K (x,s,l o (- o ty)' d- ( ^dV(l ⁰        l ‘ (- o t)^ds;

g dt ∂x l0 (v0t)

– вклад динамических процессов в точке набегания каната на барабан

l (0)

Г          7 /       P ^{( s ) d} ( Л1 < ^d 2 ² V ^{( l} 0 ^{( v} 0 ^t')^,t')

• -      ^K(x^,s,l o (v o ^{t ))}--- [Avo^A ----——---- ds

g dt             ∂x∂t l0 (v0t)

(это дополнительное слагаемое появляется при наличии неинтегрируемого граничного условия (15); при неподвижной границе (l 0 (- ₀ t) = 0) оно не исчезает из уравнения (30) , поскольку учитывает проскальзывание каната по неподвижной поверхности барабана в точке набегания. Слагаемое пропадает при устранении проскальзывания, например, посредством введения в систему прижимного ролика);

– деформирование каната, вызванное собственным весом и весом груза

l (0)

У K(x,s,l _o (v _o t)')p(s')ds.

• l 0 ( v 0 t )

• 4.    Приближенное решение задачи о колебаниях каната грузоподъемной установки без учета проскальзывания

С помощью модели (30) можно рассчитывать резонансные свойства несущих звеньев широкого круга грузоподъемных машин.

Сначала решим задачу без учета проскальзывания. В этом случае уравнение (30) выглядит следующим образом:

l (0)

\ I           i   w p(s) d ²V (s,t)   d d 9V (1_о(-_оА,А. .   .           Л ,

V(x,t) = - / K(x,s,lo(voty)-^~ — + т -----я-----~l o (- 0 1)+ Fo(^ot) ]~gds. (31)

J                  g [   dt2     dt \ dx                     / l0 (v0t)

Применим к (31) приближенный метод построения решений интегро-дифференциальных уравнений [19 –21] совместно с методом Канторовича–Галеркина [14 –18] . Введем безразмерные переменные:

£ = wox/a, т = ^ot+(^oLo-a)/vo, и новую функцию:

V (x,t) = U ( £,t ).

После их подстановки в (31) и преобразований получим интегро-дифференциальное уравнение в безразмерном виде:

U ( £,t )

ℓ 0

= -в J K(£,д,ет )

ℓ ( ε 0 τ )

U tt (S,T )+ H tt ( t ) - ^ dg -yK (£,1 о ,ет ) U tt (l o ,T )+ H tt ( t ) -^ ω ₀                                       ω ₀

Здесь K(£,д,ет ) = (w o ES/a)K(x,s,l o (v o t)) =

g — 1(ет ), £ — 1(ет ),

ς ⩽ ξ, ς ⩾ ξ,

— симметричное по ξ и ς ядро, зависящее

от времени через параметр ет , где е = — v ₀ /a; 1(ет ) = 1 + ет ; 1 0 = w ₀ l(0)/a; p(q ) = р + (mw ₀ /a~)6(q — 1 0 );

τ

F n (T ) - е / U ^ (l(eZ ),Z )l ‘ (еZ )dZ ); F n (T )

= F o ( t — y o ) ; Y o = (a — ^w o L o )/v o ; в = 1/(Sg);

γ 0

Y = ^mw 0 (ESg).

Примем: Fn(T) = B cos Wn(T), где Wn(T) — функция класса C2, B — постоянная величина. Члены, содержащие коэффициенты е2, и члены вида еF'n (т), влияющие на резонансные свойства системы как члены порядка ε2, исключим из рассмотрения. Выполнив преобразования, аналогичные проделанным в [26], и использовав асимптотический метод [21], придем к выражению для амплитуды колебаний, соответствующих n-й динамической моде:

A 2 (т ) = E 2 (т )

У F n (Z)^ n (Z)dZ + 0

У F n (Z )sin Ф n(Z )dZ

где

Е П ( t ) = —, F n (Z ) = — B - y^n, Фп^ )= W n (Z ) — W n (Z ), ^{nn                  l}{^еZ)

τ

πn k      ES                    πn         k

“ ^{0 n (ET}>= ugg ⁺n? k =mw? w ^{n (z} ^J “ ^{0 n (EZ )dz} =т^ln(1+£T)+nr

Прибегнем к методике и алгоритмам из [26] и рассмотрим явление установившегося резонанса (то есть изменение частоты внешней силы и одной из собственных частот становятся согласованными таким образом, что создаются наилучшие условия для резкого увеличения амплитуды) и прохождение системы через резонанс (когда в течение конечного промежутка времени резко увеличивается амплитуда, а мгновенная частота одного из собственных колебаний проходит через значение возмущающей частоты) [17] . Амплитуда при установившемся резонансе рассчитывается как

τ

А п (т ) = b/ -1- dZ.

1+еZ

Если W _n (т ) = т , то в области, содержащей точку т ₀ = (1/е)(пп — 1), наблюдается прохождение через резонанс. Максимально возможная амплитуда определяется формулой:

^А П ^{( т} 1 ^,т 2 )= ^Е П ^(т 2 )

У F n (Z )cosФ n (Z )dZ +

У F n (Z )sin Ф n(Z )dZ

τ 1

где τ ₁ , τ ₂ — границы области резонанса.

Выражение (34) было исследовано на достижение максимума численно, при помощи авторского программного комплекса «TB–ANALYSIS–7» [27] . На рисунке 1 показан скрин окна программного комплекса, на котором изображен график максимальной амплитуды продольных колебаний каната, возникающих при прохождении системы через резонанс на 1-й (верхняя кривая) и 2-й (нижняя кривая) динамических модах, как функции относительной скорости движения границы.

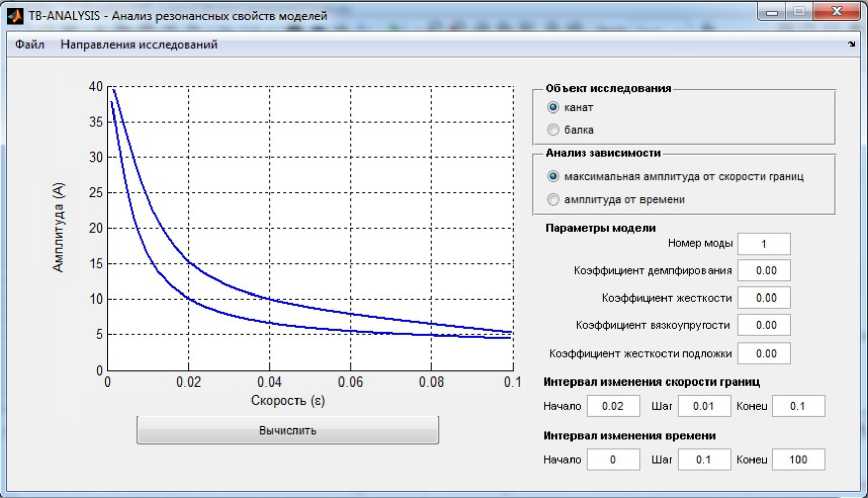
Рис. 1. Зависимость максимальной амплитуды колебаний каната от ε – относительной скорости движения его границы, на 1-й (верхняя кривая) и 2-й (нижняя кривая) динамических модах при прохождении системы через резонанс

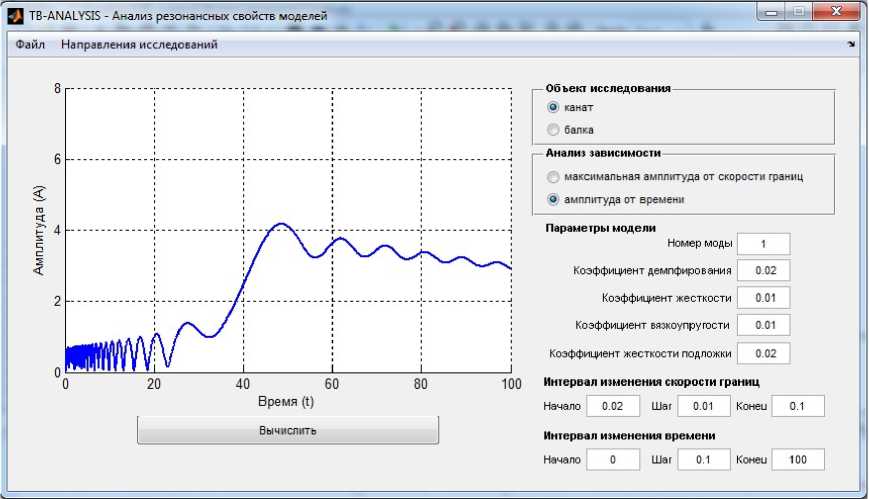
Рис. 2. Зависимость амплитуды колебаний от времени на 1-й динамической моде в резонансной области

На рисунке 2 представлен скрин окна программного комплекса, на котором изображен график зависимости от времени амплитуды колебаний каната при прохождении системы через резонанс на 1-й динамической моде.

Проанализируем связь максимальной амплитуды колебаний при прохождении системы через резонанс на 1-й и 2-й динамических модах, а также положения границ резонансной области с относительной скоростью движения границ в исследуемой задаче, описываемой как (33) . Задача была решена как аналитически (точно/exactly) [28, 29] , так и численно/approximately (см. выражение (36)) при отсутствии проскальзывания. Результаты решений сведены в таблицу 1.

Анализ данных из таблицы 1 позволяет заключить, что скорость движения границ влияет на резонансные свойства системы, а также оценить погрешность предложенного приближенного подхода к решению. Представленные параметры свидетельствуют, что максимальное отличие между точными и приближенными значениями, а значит, и погрешность метода построения решений интегро-дифференциальных уравнений, не превышает 5% при е < 0.37, что подтверждает его применимость для анализа задач, связанных с колебаниями объектов с движущимися границами, в достаточно широких диапазонах скоростей движения границ [19, 20] .

Таблица 1. Зависимость величин A n , τ 1 , τ 2 от относительной скорости движения границы ε и при прохождении системы через резонанс на 1-й и 2-й динамических модах без учета проскальзывания

	ε	0.01	0.10	0.20	0.30	0.40
1-я мода	A 1exact	23.99	7.61	5.33	4.34	3.71
	A 1approx	24.00	7.72	5.49	4.50	3.87
	τ 1exact	223.07	13.62	4.33	1.72	0.41
	τ 1approx	224.08	13.49	4.29	1.64	0.38
	τ 2exact	320.54	44.14	26.10	19.29	15.89
	τ 2approx	319.92	43.89	25.60	18.92	15.13
2-я мода	A 2exact	16.94	5.34	3.82	3.08	2.70
	A 2approx	16.95	5.49	3.95	3.20	2.82
	τ 1exact	599.48	46.66	19.55	10.97	6.81
	τ 1approx	600.37	46.48	19.29	10.60	6.44
	τ 2exact	735.41	89.91	50.06	35.82	28.12
	τ 2approx	735.92	89.53	49.43	34.93	27.12

• 5.    Численное решение задачи о колебаниях каната грузоподъемной установки с учетом проскальзывания

Решим задачу в форме (30) и учтем проскальзывание. Воспользуемся безразмерными переменными (32) и численным методом, интегрированным в программный комплекс «TB–ANALYSIS–7» [27] . Численный метод имеет в основе разностные схемы, применимые для решения нелинейных задач, описывающих продольно-поперечные колебания объектов с подвижными границами. Так, задача Коши разрешима для систем интегро-дифференциальных уравнений, в том числе с неинтегрируемыми граничными условиями.

В соответствии с численным методом, по временной координате процесс колебаний представим в виде равноотстоящих временных слоев. В пределах каждого временного слоя расчетную область разделим на фиксированное число участков одинаковой длины. Вследствие движения границ шаг по координате в разных временных слоях может отличаться. Такое разбиение позволяет избежать перехода движущейся границы через координатные узлы сетки. Для вычисления аппроксимации, что и в [27].

функций и их производных применим те же разностные

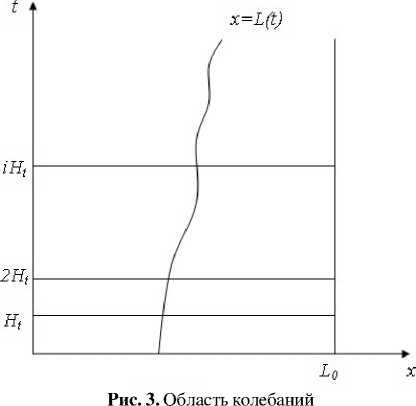
Исследуемая область колебаний изображена на рисунке 3. Здесь приняты обозначения: x — пространственная координата; t — время; L (t) — закон движения границы; i, j — номера узлов сетки; H t — шаг сетки по времени. В дискретизации по времени узлы сетки имеют индекс i (i = 0,1,2,...) и соответствующие значения времени t i = iH t . Временные слои слева от движущихся границ разобьем на Nl частей с шагом Hl i = L(t i )/Nl, а справа — на Np частей с шагом Hp i = (L 0 - L(t i' )')/Np. По оси x узлы пометим индексом j , который слева от движущейся границы изменяется от 0 до Nl, а справа — от Nl до N (N = Nl+ Np)

Назовем применяемую разностную схему схемой с переменным шагом по пространственной переменной, так как во временных слоях шаги Hl i и Hp i различны. Координаты x узлов сетки определим следующими равенствами:

(xi j = Hl i x j, 0 ^ j ^ Nl;

{ x ij = Hl i x Nl+Hp i x (j - Nt), Nl <  j <  N.

Обозначим как uk (xij ,ti) значения искомых функций в узлах сетки. Фрагмент сетки изображен на рисунке 4. Значения функций во временных слоях ti найдем последовательным переходом от одного слоя к другому, пользуясь конечно-разностным методом. Согласно итерационной процедуре на его основе, по известным значениям искомых переменных на временных слоях ti-1 иti определим их значения на следующем слое ti+1. Внутри этого временного слоя cначала вычислим значения функций во внутренних узлах новой сетки через разностные аппроксимации исходных уравнений, интерполированных полиномами Лагранжа, для согласования с предыдущими слоями из-за подвижности сетки. Затем установим значения на движущейся границе каната из граничных условий с помощью односторонних разностных производных. После этого рассчитаем все необходимые производные в новом слое ti+1 через разностные аппроксимации значений функций в узлах сетки. Этот цикл повторим на последующих временных слоях промежутка моделирования. В пределах слоя для определения функций и их производных используем аппроксимации с точностью до членов 2-го порядка малости относительно Hli , Hpi , Ht . Это позволяет отыскать решение задачи при любом значении времени t.

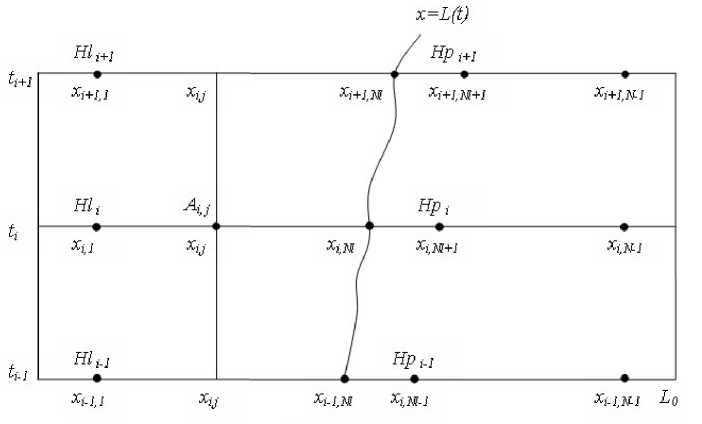
Рис. 4. Фрагмент расчетной сетки

Для реализации вычислений прибегнем к программному комплексу «TB–ANALYSIS–7», разработанному в среде MATLAB. Результаты с учетом проскальзывания сведем в таблицу 2. Из таблицы видно, что при прохождении системы через резонанс амплитуда колебаний каната грузоподъемной установки с учетом проскальзывания является оценкой сверху для амплитуды без учета проскальзывания.

Таблица 2. Зависимость величин A n , τ 1 , τ 2 от относительной скорости ε при прохождении системы через резонанс на

1-й и 2-й динамических модах с учетом проскальзывания

	ε	0.01	0.10	0.20	0.30	0.40
1-я мода	A 1N um	25.38	8.76	5.47	4.72	4.24
	τ 1N um	238.57	14.83	4.29	1.85	0.51
	τ 2N um	342.48	47.53	27.43	20.74	17.45
2-я мода	A 2N um	18.43	5.41	4.19	3.40	2.79
	τ 1N um	641.84	49.23	20.42	11.24	7.89
	τ 2N um	785.43	93.80	55.89	38.38	28.02

• 6.    Выводы

В проведенном исследовании применен разработанный авторами подход к решению задачи продольных колебаний каната грузоподъемного устройства с учетом важного фактора — проскальзывания каната по поверхности барабана и построена соответствующая математическая модель. Поставленная неклассическая задача с движущимися границами и неинтегрируемыми граничными условиями сводится к интегро-дифференциальному уравнению с симметричным зависящим от времени ядром и перемененными пределами интегрирования. При отсутствии проскальзывания с приемлемой точностью получено приближенное решение методом, сочетающим метод построения решений интегро-дифференциальных уравнений и метод Канторовича–Галеркина. Для полного исследования системы с проскальзыванием использован специализированный авторский программный комплекс, реализующий разностную схему с переменным шагом по пространственной переменной.

Полученные результаты демонстрируют существенное влияние проскальзывания на резонансные характеристики системы. Установлено, что учет проскальзывания приводит к увеличению амплитуды колебаний по сравнению со случаем «идеального» контакта каната с барабаном. Анализ явления установившегося резонанса и прохождения системы через резонанс выявил отличия в зависимостях амплитудных характеристик от относительной скорости движения границы для разных динамических мод.

Разработанная математическая модель и примененный подход представляют практическую ценность для расчета и оптимизации динамических характеристик грузоподъемных устройств, поскольку позволяют более точно прогнозировать их поведение в резонансных режимах. Полученные результаты дают возможность на этапе проектирования предотвратить возникновение продольных колебаний значительной амплитуды в несущих элементах грузоподъемных установок, а также открывают перспективы для дальнейших исследований, в том числе с учетом нелинейных свойств применяемых материалов, поперечных колебаний каната и другого. Приведенные решения могут быть использованы при изучении колебаний механических объектов с движущимися границами, например, таких как рассматриваемые в [30–33].