Об одном случае решения в замкнутой форме краевой задачи Маркушевича для полуплоскости

Рассмотрим трехэлементную задачу Маркушевича

¥ + ⁽ t ) = a ⁽ t > _ ⁽ t ) + b ⁽ t > + ⁽ t ) + f ⁽ t )                               (1)

на вещественной прямой Г :Im z = 0. Здесь a ( t ), b ( t ), f ( t ) e H ( Г ) - гельдеровские функции, a ( t ) ^ 0, t еГ , бесконечно удаленная точка включается в Г .

Требуется найти функции у+ (z), у- (z), аналитические соответственно в верхней полуплос кости S+ и нижней полуплоскости S-, непрерывно продолжимые на прямую Г, если граничные значения этих функций связаны линейным соотношением (1). Решение будем искать в классе функций, исчезающих в точке z = -i, которые чаще всего требуются в приложениях.

Пусть к= Ind _Г a ( t ) = ^ П [ ln a ( t ) ]| ⁺

. Так как a(t) удовлетворяет условию Гельдера в окрестности бесконечно удаленной точки, то a(+м) = a (-~) ^ 0.

Для того, чтобы привести рассматриваемую задачу к случаю конечной граничной задачи для единичной окружности, рассмотренной в статье [3], применим следующее дробно-линейное преобразование:

. f - i         .z - i

z — — i -----, с — — i ----.

f + i        z + i

При этом преобразовании прямая Г плоскости z переходит в единичную окружность L: |^ = 1 плоскости f . Если точка t пробегает в положительном направлении прямую R, то со ответствующая ей точка т плоскости f, определяемая равенством

. t — i т — — i--- t + i описывает окружность L в направлении, оставляющем слева ограниченный ею круг. Этот круг мы обозначим через D+, а часть плоскости, внешнюю по отношению к D+, - через D—.

Дробно-линейное преобразование (2) конформно преобразует область S+ в область D+, а об ласть S— - в область D—; при этом точке z = ^ соответствует точка f = -i, а точке f = ^ - точка z = -i [2].

Для того, чтобы не усложнять внешнего вида формул, мы будем обозначать функцию

Г f - i

'Л z) = И - i^— ( f + i просто через ^(f); аналогично поступаем для функций a (t), b(t) и f (t), а также для других функций, которые нам встретятся в дальнейшем.

При этих обозначениях граничное условие (1) з апиш ется в виде:

• V + ( т ) = a( т ) ^ - ( т ) + b( т> + ( т ) + f ( т ), т е L .                        (3)

Наложим следующие дополнительные ограничения на коэффициент b ( t ) краевой задачи (1):

• а)    b ( t ) a^ + 1 * 0, t еГ ;

a + ⁽ t )

• б)    b ( t ) a ^{+ (} t ) + 1 - является краевым значением аналитической и отличной от нуля всюду в a + ( t )

области S- функции, за исключением, быть может, z = -i, в которой она имеет конечный поря док к1. Здесь a(t)=a + (t)tKa-(t)- факторизация коэффициента a(t) по формулам Гахова [1].

Очевидно, что в этом случае функция b(т) краевой задачи (3) будет удовлетворять следую щим условиям:

а) Ь 1 ( т ) + 1 * 0

( ь1(т) = b (т) V

a +T' a + ( т ) J

, те L;

• б)    b 1 ( т ) + 1 - является краевым значением аналитической и отличной от нуля всюду в области D - функции, за исключением, быть может, бесконечно удаленной точки, в которой она имеет конечный порядок к 1 .

Теперь мы можем воспользоваться результатами статьи [3]. В этой статье краевая задача Маркушевича для единичного круга сводится к сингулярному интегральному уравнению относительно Re ^ ₊ ( т ) с последующим решением задач Шварца и Гильберта в классе кусочноаналитических функций. Общее решение неоднородной задачи Маркушевича для единичной окружности было получено в виде

^ ( S ) = ‘

a + ( s )

_ 2niLT - s

d т + G ( s ) + P k ₀ — 1 ( S ) , _$е D + ,

a ' - "" b ^' ¹ -LJ g ^ d T + G( 5 ) + P ^ - , ( f ) , ;e D - .

2 п i L ^T - s               ⁰ _

ςκ

Здесь    g^{( т} ) = ^Ь 1 ^{( т} ) [ d + P K - 1^{( т )} ] ^- ibBV Г F o ^{( т ) +} Q k - 1^{( т} ) ⁺ Q k - 1^{( т )} ] ,    ^{G (} S ) = В J g ¹ ^ ^{dт ,}

- o        bT) + 1L           1          1 J             2niL т-s д1(т) =

Ь 1 ( т )

f ( т )

-

b ( т ) + 1 L a ₊ ( т )

iF^( т ) ,

F o ( S ) = ^J 2 n i L

c (т)(т + S) (т - ST

d т , F ( s ) = -^flm| f ^{( т )} | ^{т + S} d т , ¹      2 n i L [ a ₊ ( т )( т - s ) т

c(T) = Im{( b1(T) + 1)[ d + PK0-1(т)]} , К0 = IndL   T    = К - К„ К1 = IndL (b1(T) + 1) , b1(T) + 1

P _K 0 - 1 ( s ), Q k : _{1 - 1} ( 5 ) — произвольные многочлены степени не выше к ₀ - 1, к_х - 1 соответственно.

Если к₀<  0, то появляются условия разрешимости задачи

L

2 b 1 ( T )Re ^ ₊ ( т ) ( b 1 ( T ) + 1) ,

?-1 dT - 1

L

f ^{( т} ) a + ( т )( b 1 ( T ) + 1)

т^{к 1} d T = 0, k = 1,

^-K 0 ,

где

Re ^ + ( т ) = ¹ ( b 1 ( т ) + 1)[ d + P k 0 - 1 ( т ) - Ф 1 ( T )] + _; f ^{( T )}- , 2                                  2 a ₊ ( т )

- i V 1 ( S ) =

1 b 1 ( s ) + 1

F 0 ( S ) + F 1 ( S ) + Q k 1 - 1

( S ) + Q_k . - 1 ( S *)

При к _х <  0 возникают следующие условия разрешимости

/ cB dT=ak, ak=-j Im Lτ                 L

I fw 1 т , k = 0 f \ _ k + 1

[ a + ( t ) т

-к^|.

Если f ( т ) = 0, то мы имеем однородную задачу Маркушевича. В этом случае G ( s ) = 0 .

z - i

Вернемся теперь к переменной z по формуле q = - i ---.

z + i

Тогда общее решение неоднородной задачи Маркушевича для полуплоскости запишется в виде

Здесь

a ₊

+∞

[ ( —i) gO dt + G(z) + p  (—i к -1

^J V t + i j t - z                ⁰ V z + i

, z ^е S ₊ ,

^ ( z ) = ‘

-∞

κ

g ⁽ t ) = b i⁽ t ) d ⁺ P 0 - 1

G ( z )

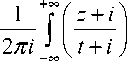
g "¹ dt , t - z

g 1⁽ t ) =

+∞ f <---i_) gt) dt + G(z) + p   (---i к -1

^J V t + i J t - z                ⁰ V z + i

, z е S - .

-∞

t - i t + i

^b 1⁽ t ) b 1 ( t ) + 1

-

^ib1⁽ t ) b i ( t ) + 1

F ( t ) + Q k - i I t-¹ . I + Q k - i I H

¹ V t + i j ¹ V t + i

,

f ( t ) a + ⁽ t )

- iF f( t )

+∞

F o( z ) = -f π i

c ( t ) dt

-∞

t

-

1 +Г c ( t ) tdt n i ^J t ² + 1 ,

-∞

_ . 1 7_T f f ( t ) 1 dt 1 ⁺l_t f f ( t ) 1 tdt

F ₁ ( z ) = — Im V^-^r--- Im --, n i ¹       a , ( t ) t - z n i ^J       a , ( t ) t ² + 1

-∞     +              -∞     +

c ( t ) = Im ^ ( b 1 ( t ) + 1)

z d+P

^K 0 ^{- 1}

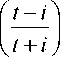
I z - i ) „ I z - i )                                                            ( z - i )

PK -I----I, Qk -I----I - произвольные полиномы относительно I----I степени не выше 0 V z + i j     1 V z + i j                                                 V z + i j k0 -1, к1 -1 соответственно.

Условия разрешимости (5), (6) запишутся, соответственно, в виде:

где

+∞

J

-∞

2 b₁ ( t ) Re ф₊ ( t )

( b 1 ( t ) + 1) ,

,     K - 1             +l                   f . k.k - 1

t - i | dt г         j ( t )        [ t - i ] dt

I --                                ”1I t + i j (t + i)2    -^ a + (t)(b1(t) +1) V t + i j    (t + i)2

= 0, k = 1,

- К ), (8)

Re ф + ( t ) = 2( b 1 ( t ) + 1)

т T-x I t - i I - Z X d + Px- 1 ---- - ^ (t)

^K 0 ^{- 1} V t + i j

₊ f ( t ) , 2 a ₊ ( t ),

^- . Ф 1 ^{( z} ) =

b 1^{( z} ) ^{+ 1}

F 0 ( z ) + F 1 ( z ) + Q k - 1 1       I + Q k - 1 1       I

¹ V z + i j     ¹ V z + i j

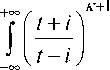
c ( t ) dt                ⁺p 1 1 + i | ^{K +1} _T f f ( t ) 1 dt

—^X-^J—T = a_k , a_k = - I---I Im Г------ ( t + i )²                  -L V t ^{- i} j        [ a + ⁽ t )( t + i )²

k = 0,

^{- K} 1 .

Результаты статьи [3] позволяют сформулировать следующие теоремы.

Теорема 1. Пусть коэффициенты однородной задачи Маркушевича (1) ( f ( t ) = 0)

a(t), b(t) е H(Г), a(t) ^ 0, t еГ, к = Indra(t), а также функция b1(t) +1 является краевым значением функции на прямой Г, аналитической и отличной от нуля всю^у в области S- и Г, за исключением, быть может, точки z = -i, в которой она может иметь конечный порядок к1, к0 = к - к1.

Тогда однородная задача (1) (f (t)=0 ) в классе кусочно-аналитических функций, исчезающих в точке z = -i:

• 1)    при к ₁ >  0, к ₀ >  0, имеет общее решение, определяемое формулой (7) (G ( z ) = 0 ), которое

линейно зависит от 2 к ₀ + 2 к ₁ = 2 к произвольных вещественных произвольных постоянных;

G ( z ) = 0, P_K , ---- 7 0 , ко’        ^{К 0 - 1} V z + i I j

• 2)    при к ₁ >  0, к ₀ <  0, общее решение задается формулой (7)

торое содержит 2 к ₁ - r произвольных вещественных постоянных, r₁ - ранг матрицы коэффициентов однородной системы (8) (если r₁ = 2 к ₁, то задача имеет только тривиальное решение);

• 3)    при κ ₁ ≤ 0,    κ ₀ ≥ 0,    имеет общее решение, определяемое формулой (7)

( X             ( Z - i 1 ТХ^                  X

G ( z ) ≡ 0, Q         ≡ 0 , которое содержит 2 κ - r произвольных вещественных постоян-

V       1^ V z + i J  J                     0

ных , r – ранг матрицы коэффициентов однородной системы (9) (если r = 2 κ ₀ то задача, отличного от тривиального, решения не имеет);

• 4)    при κ ₁ ≤ 0, κ ₀ <  0, если функция b ₁ ( t ) + 1 удовлетворяет условиям (9) ( f ( t ) ≡ 0 ) и условиям (8) ( f ( t ) ≡ 0 ), имеет одномерное пространство решений, определяемое формулой (7) („,             ( z - i ^           ( z - i 1

I G(z) = 0, PK -1II = 0, QK -1II = 0 I; в противном случае имеет только тривиальное ре-V               0 V z + i J 1 V z + i J J шение.

Теорема 2. Пусть коэффициенты неоднородной задачи Маркушевича a(t),b(t) ∈ H(Γ) , функция f (t)∈ H(Γ), a(t) ≠ 0, t∈ Γ, а также функция b1(t) +1 является краевым значением на прямой Γ функции, аналитической и отличной от нуля всюду в области S- ∪ Γ , за исключением, быть может, точки z = -i, в которой она может иметь конечный порядок. κ1 .

Тогда неоднородная задача в классе кусочно-аналитических функций, исчезающих в точке z = - i :

1) при κ1 > 0, κ0 ≥ 0 имеет общее решение, определяемое формулой (7), которое линейно за- висит от 2κ произвольных вещественных постоянных;

2) при κ ₁ >  0, κ ₀ <  0 общее решение задается формулой (7)

P κ ₀ - 1

z - i z + i

≡ 0

если выпол-

няются -κ0 - r1 условий разрешимости, выписанных явно (r1 – ранг матрицы коэффициентов системы (8)), которое содержит 2κ1 - 2r1 произвольных вещественных постоянных (если r1 = κ1 , решение будет единственным);

1^1 z - i I 7x1

• 3)    при κ ≤ 0, κ ≥ 0 имеет общее решение, определяемое формулой (7) Q         ≡ 0 ,

1        0                                                                                  ( 1 V z + i J     J если выполняются -κ1 + 1 - r условий разрешимости, выписанных явно (r – ранг матрицы ко- эффициентов системы (9)), которое линейно зависит от 2κ0 - 2r произвольных вещественных постоянных (при r =κ0 решение будет единственным);

• 4)    при κ ₁ ≤ 0, κ ₀ <  0 имеет единственное решение, определяемое формулой (7)

( z - i 1             ( z - i 1     1

PK -11I = 0, QK -11I = 0 I, тогда и только тогда, когда выполняются -к1 +1 условий 0 V z + i J 1 V z + i J     J разрешимости (9), и -κ0 условий разрешимости (8).