Об одном способе приближения области асимптотической устойчивости дифференциально-разностных систем

ОБ ОДНОМ СПОСОБЕ ПРИБЛИЖЕНИЯ ОБЛАСТИ АСИМПТОТИЧЕСКОЙ УСТОЙЧИВОСТИ ДИФФЕРЕНЦИАЛЬНОРАЗНОСТНЫХ СИСТЕМ

У. П. Зараник, А. П. Жабко

В статье рассмотрена нелинейная стационарная система дифференциальноразностных уравнений с одним запаздыванием. Найдено приближение решения дифференциально-разностной системы решением разностной системы уравнений. На основе полученных оценок построено приближение области асимптотической устойчивости системы с запаздыванием. Предложены способы описания области асимптотической устойчивости дифференциально-разностной системы. Приведен иллюстративный пример. На основе полученных оценок построено приближение области асимптотической устойчивости системы с запаздыванием в функциональном пространстве.

Введение. Для построения области асимптотической устойчивости дифференциально-разностной системы уравнений запаздывающего типа был разработан подход, состоящий из двух этапов. Первый этап заключается в приближении решений дифференциально-разностной системы уравнений решениями разностной системы и оценки близости полученных решений. Второй этап состоит из построения области асимптотической устойчивости разностной системы уравнений и описания приближаемой области асимптотической устойчивости дифференциально-разностной системы, используя оценки приближения соответствующих решений, полученных на первом этапе.

Рассмотрим дифференциально-разностную стационарную систему вида

T = /(z(t), x^t-T))        (1)

с начальной функцией p(i), t е [-Г; 0], где /(^(t), E(t — Т)) - непрерывная функция своих аргументов. Будем предполагать, что система (1) имеет нулевое решение /(0, 0) — 0 и линейное приближение

£№ = Ay(t) + By^t - Т)

экспоненциально устойчиво по Ляпунову.

Схема метода Адамса. Предположим, найдено несколько значений х, в моменты времени tj, $j = ж(А), j = 0,i, tj = to + jA. Требуется получить правило для вычисления т<+1 ж х(А-ц) на следующем шаге.

Интегрируя правую и левую части системы (1) по промежутку ^,t^+l], получаем: ti+l

х(£,+1) = х(А) + J /(x(£),x(£-T))ci£.    (2)

Попытаемся адаптировать алгоритм метода Адамса [1] для построения решения дифференциально-раз постных уравнений. Заменив подынтегральную функцию интерполирующим ее многочленом ^(t), будем считать дискретные приближенные значения /, = /(tj,Xtj) ^ /(х(£₃-), x(tj — Г)) известными. При интерполировании назад из узла А имеем

Рк^ = Р,(А + qh) - Л 4- ?ДЛ^ + ^^Д2Л^ + ^^^Л-з + -+ g(g + l) ■ а из узла £<+1

ЗД) = Шт + э*) = /i+1 + Wt + ^—^ Д2А-1 + ^^"^Д3/^ + ...+

9(9 + 1)

A (?4Ь-1) _Afc, —        Л Ji ц_;.

Подставим многочлены Pk^t), Pk(t) в равенство (2) .^ Используя конечные разности, получаем формулы для вычисления очередного значения х,+1 ~ $(ti-n)

t<+i xi+i=xi+ J Pk^dt,     (3)

Xi₊i = Xi 4 / P^dt.     (4)

На основании формул (3), (4) получаем два семейства многошаговых методов Адамса.

Рассмотрим первое семейство методов (3).

Сделаем замену переменных £ = £, + qh в ин- ®<+1

теграле J Pk^dt ti-ц                 i

J Pk^dt = hf Pk(ti + qh,)dq, tj                   о

Тогда формула (3) может быть переписана в виде

Xi^-i ™ Xi Ч~ Mfc_?

где

!к = I Pk^ti +qh)dq = о

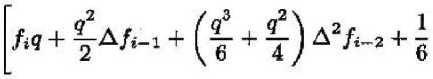
/ 4           \

/ 9 г 3 I 2 I дЗ /     ।

(   4 q 4 q I А Л-з+

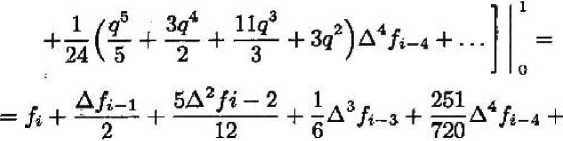
Ограничиваясь методом Адамса четвертого порядка, получаем

Xi₊1 = Xi + /t(/i 4 1дл^ + ”Д²Л-= + U³fi-3 + ^А⁴А-4).

Сделаем аналогичную замену в (4) t = tj+i+gh. и, подставляя выражение Pk(t),

Ik — J Pk(ti+1 + qh^dq = Л+19 + —ДЛ получаем равенство зц-н где

= Xi + hlk,

x

хД /i-2 + 24

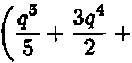
у**')

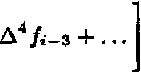
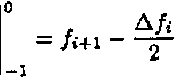
Д3/1 - 1

Следовательно, xi+1 = Ti + hh^x - Vh - ^Д2Л-1-^Д3Л-2 - ^А4Л-з).        (6)

Можно заметить, что первое семейство методов (5) является явным, а второе (6) -неявным.

Основные утверждения и свойства области асимптотической устойчивости.

Предположим, что правые части уравнений fc4 1 раз непрерывно дифференцируемые функции. Тогда ошибка на шаге составляет

КкИ = ^м1** ■ х (»+У'-‘+1

Таким образом, локальная погрешность метода, вычисляемая по формуле 1

Следовательно, справедливо следующее утверждение.

Утверждение. Локальная погрешность (5), (6) методов Адамса составляет O(hfe+2) и O(hfe) соответственно.

Рассмотрим семейство разностных уравнений

y(t + h) = y(t)+ +Р^ьШ_1У^-^,...,у(1-Н)\

Линейное приближение системы (7) экспоненциально устойчиво, т. е. справедливо предельное соотношение yhtt, у?) -> $(t, уз) при h -» 0, t G [0; Т], где yh(t, у?) - решение системы (7) при t > 0.

Лемма 1. Для любого 0 <  h < /io существует йв такое, что линейное приближение системы (7) является экспоненциально устойчивым по Ляпунову.

Далее будем предполагать, что $(t, уз) -решение дифференциально-разностного уравнения с начальной функцией y(t₀ -Ь ■) и yW ~ решение разностного уравнения.

Рассмотрим приближение области асимптотической устойчивости разностного Аг и дифференциально-разностного уравнения

Л = {х : т € <ад(СА) П ||$II < 1}.

В область асимптотической устойчивости разностного уравнения Л_Е входят кусочнонепрерывные функции с ограниченной первой производной ||у?(£)|| <  S > 0, для которых выполнено условие y(tfc) = y(ik), где tk G МГ;0) - точки разбиения отрезка №0).

Лемма 2. Пусть y3(t) € Л_е, е > 0 такое, что >Ц/ 0. Тогда для любого 5 > 0 существует Ьци Н> 0 такое, что справедливо неравенство

||Ук(-й,у>)||т < 5, 0 <  h < hi.

Доказательство. 3 Н : ||$(t, р)|| < - при t>R Тогда Ы (#.)!!< ||ул.(/?,р) - $(Я,^)||+ +l№v>)ll < ^^ + 2^ + ||$(Я,^)||.

Если Kh^fe + ²^ < ^5, то ||y/i(fl_Ty’)|| < 5-

Теорема. V е > 0, 3h₂ > 0 такое, что 0 < h < h-2 справедливо включение,

Ле С Лк

Доказательство. V 0 < h < ho система (3) экспоненциально устойчива, следовательно 3 р > О такое, что в этой зоне. Уравнения динамики имеют следующий вид

{? : kll

= -l/Tl(t)[l + xi(t)J -ft®i(t)+

По лемме 2 5 = р, ha — min{/io, /ii}, следовательно ||ук(Д,¥>)||т <  Р при Ы^,^) е Л^

Рассмотрим свойства области асимптотической устойчивости дифференциальноразностного уравнения Л :

• 1.    Положительная инвариантность. V^o € € Л => x^t,^ определено при t > 0 и x(t, <р) -> 0 при t -> +оо.

• 2.    Л открытое множество.

• 3.    Л - связное множество V^ и ^ е Л ^ 3^x(t) е С([—Т;0)) при А е [0; 1] такая, что у>д(?) £ Л при А £ [0; 1], Po(t) = V^ и tp^t) = £^.

Методы описания области асимптотической устойчивости дифференциально-разностных систем.

Так как область асимптотической устойчивости содержится в некотором функциональным пространстве, то возникает проблема ее описания в этом пространстве. Предложим некоторые способы описания области асимптотической устойчивости:

• 1.    Сечение области асимптотической устойчивости при t — 0.

• 2.    Сечение области асимптотической устойчивости при t = — Т.

• 3.    Огибающая области асимптотической устойчивости:

• 4.    Пространство среднеквадратичных о

• 5.    Эмиттанс p(t,xi,..., х_п) = j ^Ц, где

{(УьУг,--, Уп) | Уз = ^ах^Д^з = 1,п}.

значений |(уГ,^,..., ^Г) | ^7 = ^ ^2(f)dtj.

-т

D

D = <р 6 Л, ^» (t) = X_S18 — 1 , п.

Пример. Рассмотрим реактор, состоящий из двух активных зон [2]. Будем считать, что реактивность в 1-й и 2-й активных зонах реактора зависит только от уровня мощности

+axa(t — Г),

Z-T- = -i/X2(t)[l + Ж2(t)] - QX2(t)+ at

+o$i(t -Г), где I — время жизни нейтронов; а — коэффициент, характеризующий связь между 1-й и 2-й активной зонами; v = yN, где у - величина отрицательного мощностного коэффициента реактивности; N - мощность; Т - время запаздывания (м > 0,I > 0, а > 0, Т > 0). Исследуем данную систему уравнений на устойчивость двумя различными способами.

Первый способ заключается в аналитическом исследовании корней квазиполинома линейной части рассматриваемой системы, который имеет вид:

(iA + a + ь)² = а²е^1ХТ

Получаем следующий результат: при a > 0 имеем абсолютную устойчивость, при a < 0 устойчивость для Т G [0, Т), где

2^—^(1/4-2a)

где р = arc tan

у^,-ф + 2a) a + v

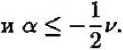
Второй способ заключается в построении области асимптотической устойчивости системы с запаздыванием с помощью вышеизложенного метода Адамса в среде MATLAB. Построение графиков и их анализ подтверждают существование зависимости области асимптотической устойчивости от параметров системы.

Построение графиков и их анализ показывают, что существует зависимость области асимптотической устойчивости от параметров системы Т, а, и, I. Так на рис. 1 продемонстрирована зависимость a — у.

Рис. 1. Зависимость параметров системы а--v

Результаты первого и второго способа согласуются между собой и уточняют данные, полученные в [2]. где показано, что область асимптотической устойчивости имеет следующий вид:

yATW^W < V2, который не зависит от параметров системы.

На рис 2. изображено сечение области асимптотической устойчивости системы (8), где множество В - проекция области асимптотической устойчивости дифференциальноразностного уравнения без ограничения на производную и множество С — проекция области асимптотической устойчивости дифференциально-разностного уравнения с ограничением па производную : |^(t)|| = 1.

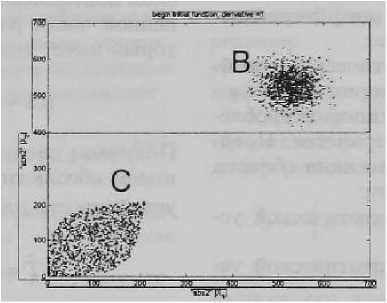
Рис. 2. Сечение области асимптотической -устойчивости при t — —Т

На рис. 3 представлена огибающая области асимптотической устойчивости., по осям JVi(—Т), Х2(™Т) - координаты начальной функции

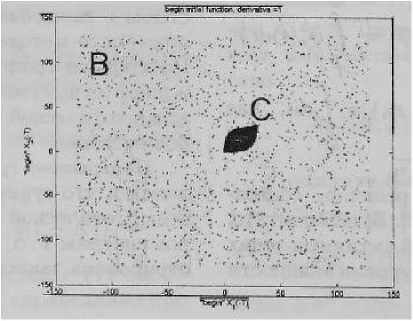
Рис. 3. Огибающая области асимптотической устойчивости

На рис. 4 изображен эмиттанс, который показывает распределение плотности точек на поверхности области асимптотической устойчивости. Чем светлее поверхность, тем больше плотность точек, которые принадлежат области асимптотической устойчивости.

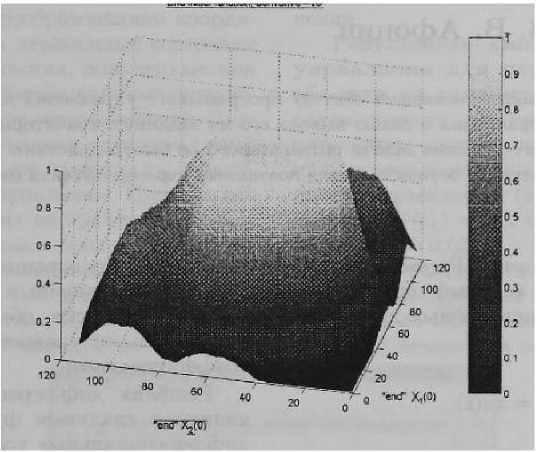
Рис. 3. Эмиттанс

Второй способ построения области асимптотической устойчивости был реализован в среде MATLAB. Таким образом, подтвердился результат, полученный при аналитическом исследовании квазиполинома системы. Приведенные способы описания области асимптотической устойчивости дифференциально-разностных систем в функциональном пространстве дают более полную картину для исследования системы дифференциально-разностных уравнений.