Об описании предельного спектра ленточных тёплицевых матриц

Введение. Тёплицевы (и связанные с ними ганкелевы) матрицы — это один из наиболее важных для приложений класс матриц, появляющийся в задачах фундаментальной математики, теоретической физики, механики, а также в многочисленных инженерных приложениях [1].

В данной работе рассматривается задача описания предельного множества последовательностей собственных значений ленточных тёплицевых матриц растущих размеров (предельного спектра) с заданным символом, как множества решений некоторой системы алгебраических уравнений и неравенств. Основной результат работы состоит в построении алгоритма, строящего такую систему алгебраических уравнений и неравенств. Отметим, что этот алгоритм рассматривается лишь в частном случае, с целью более выпукло представить основные идеи авторов.

Задача описания предельного спектра является важной и трудной задачей спектральной теории тёплицевых операторов, имеющей многочисленные применения в математической физике. Впервые такая задача была исследована Ф. Спитцером и П. Шмидтом в работе [2] (см. также работы [5], [6], посвящённые исследованию этой же задачи). Ф. Спитцер и П. Шмидт показали, что предельный спектр является аналитическим одномерным множеством, точнее, он либо состоит из одной точки, либо является объединением конечного множества аналитических дуг.

Позднее Дж. Ульман доказал связность предельного спектра [3]. Несмотря на столь почтенную историю вопроса описания предельного спектра, до сих пор нет алгоритмически эффективных способов его точного нахождения. В данной работе несколько усиливается результат, описанный в [2], и доказывается, что предельный спектр является полуалгебраическим множеством.

Данная работа выполнена при финансовой поддержке федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» в рамках мероприятия 1.2.2 (госконтракт номер П1116), а также при финансовой поддержке Министерства образования и науки Российской Федерации, соглашение 14.А18.21.0356 «Теория функциональных пространств, операторов и уравнений в них».

Постановка задачи. Пусть f — комплекснозначная функция, аналитическая в окрестности окружности единичного радиуса S¹ = {z е С: |z| = 1]:

r(z)=£3lz‘.                              (1)

keZ

Будем обозначать через Тп^ тёплицеву матрицу размера пхп, то есть матрицу Тп^^а,^ т, матричные элементы которой задаются формулой ам = ан, где ак находится из уравнения (1). Отметим, что у тёплицевой матрицы на каждой из диагоналей, параллельных главной, стоят одинаковые элементы. Если для к < -г и для к > h ак =0, то есть аналитическая h функция f (z) превращается в лорановский полином f (z) = ^ akzk > т0 соответствующая такой к=-г функции тёплицева матрица называется ленточной.

Упорядочим собственные значения {АЛ|/]”1 матрицы Тп^ так, что |А„,|<|Ал;| при /< j. Множество предельных точек последовательностей {Ал,}” будем называть предельным спектром последовательности тёплицевых матриц ^Тп (f )}л и обозначать через о, (f).

Цель настоящей работы — установить связь между предельным спектром и функцией f (z) (которую также называют символом каждой из матриц последовательности {^„(ОЕ-Р’ От метим, что последовательность {а^}“ ш является последовательностью коэффициентов Фурье-Лорана функции f (z).

Классическая теорема Сегё, которую также называют слабой теоремой Сегё [1, 4], утверждает, что в случае, когда символ является вещественнозначной функцией, а матрицы Т_п (Г) являются самосопряжёнными, предельный спектр последовательности тёплицевых матриц \Т_П с образом символа функции f (z): t " V ')п=1                                                   ' '

o/(f) = /?(f) = {f(z):zeS1}.                              (2)

В общем случае связь между предельным спектром о, (f) и символом f (z) является гораздо более сложной, и при рассмотрении большого числа примеров кажется случайной. Тем не менее, как показано ниже, эта связь существует, так, что по символу в результате некоторой алгоритмической процедуры вычисления можно найти предельный спектр. Этот результат является уточнением классических результатов Ф. Спитцера и П. Шмидта, являющихся в значительной степени теоремами существования.

Классические результаты. Приведём классические результаты Ф. Спитцера и П. Шмидта об описании предельного спектра о, (f) последовательности ленточных тёплицевых матриц Свяжем с символом ленточной тёплицевой матрицы f(z\ = V^h, a.z^k многочлен

Q^z.k^z'^f ^-\^ = а г + a_r+1z + ... + (a0-A)zr +... + ahzr+h. Тогда имеет место следующая теорема.

Теорема 1. (Ф. Спитцер, П. Шмидт, [2]). Пусть z_Y (A),z₂ (A),...,z_r+/, (А) — комплексные корни многочлена Q(z,A), с учётом их кратности, упорядоченные по возрастанию их модулей, а, (А) = |z_z (А)|. Тогда предельный спектр описывается следующим условием:

a,('’) = {^C|o,W = o„iW!- (3)

Основные результаты. В данном разделе описан предельный спектр как множество решений системы полиномиальных уравнений и неравенств. Рассматривается также алгоритм нахождения этой определяющей предельный спектр системы алгебраических уравнений и неравенств.

Прежде всего, напомним важное в дальнейшем понятие результанта многочленов нескольких переменных [5]. Эта конструкция не является так же хорошо известной как результант двух многочленов от одной переменной. Идея определения результанта в общем случае состоит в следующем. Пусть имеется система алгебраических уравнений, левую часть которой составляют многочлены множество решений которой х,,...,х,„ — конечно, и полином а. Произведение значений многочлена g в точках, являющихся общими корнями многочленов системы, называют результантом:

/V

Res(f1,...,f„;g) = ng(xJ.

k=l

Следует ещё раз отметить, что многочлены f_x,--,f_n е /с[^,...,^] являются многочленами от многих переменных. Поле к удобно считать алгебраически замкнутым, в нашем случае можно ограничиться случаем к = С . В этом случае по теореме Безу (в случае общего положения) множество общих решений состоит из N = г_х -...-r_n решений, где r_k = deg(f_k'),k = 1,...,п . Возможны модификации этого определения. Например, g = g^.—.t^, и результант равен значению многочлена g в общих корнях системы уравнений f_x (х) = 0,...,Г_л (%) = 0. При этом система может состоять и из одного многочлена. Способы вычисления результанта могут быть разнообразными, но, по существу, в конечном итоге сводятся к использованию методов коммутативной алгебры и выборам специальных базисов. Удобно использовать, так называемые базисы Грёбнера, связанные со специальными упорядочениями множества мономов [6]. Ниже используется одно из таких упорядочений.

Напомним определение результанта в случае двух переменных (и трёх многочленов). Пусть flzf2 е/r[xlzx2] — многочлены двух переменных с коэффициентами из поля к, X =(xvx^. Далее ограничимся случаем, когда к = С совпадает с полем комплексных чисел. Пусть deg(^) = л,, / =1,2, N = пх-п2. Рассмотрим также многочлен g е *[Х]. Мы хотим определить результант Res(fvf2;g^, как выражение пропорциональное произведению значений много члена g в общих нулях многочленов fx,f2. Выберем упорядоченный базис:

М = {м^ = х^х^ |0 < ^ < л_и0 <  р₂< n₂;k = 1,...,Л/}.                     (4)

Будем называть элементы из этого множества М степенными произведениями. Многочлен Л(х) е/c[x_lzx₂] называется приведённым относительно М, если он представляется в виде линейной комбинации степенных произведений из М . Можно показать, что для многочленов общего положения f_vf₂ е /с[х₁,х₂] можно редуцировать произвольный многочлен />(х) е/c[x_lzx₂] по модулю многочленов f_vf₂, то есть найти такие многочлены a_va₂ е /r[x_lzx₂], что многочлен h_rad (x_vx₂^ = h (х,,х₂) - a, (х,,х₂) f_x (х,,х₂) - а₂ (х,,х₂) f₂ (х,,х₂)

является приведённым относительно М. Пусть X_x,...,X_N — множество общих нулей многочленов ^,f₂. Тогда, очевидно, что h_red^X^ = Ь^Х^Д< j

Приведём многочлены ц^(%)-д(%),% = (xlzx2), по модулю Ми обозначим получившие'

ся многочлены через д_к:

М, (ху (%) = а_к1 (ху (X) + а_к2 (ху (X) + д_к (X) д_к Р0 = М (xy... + b_kN\i_N (х).

Подставляя X = Xj в приведённые выше равенства, мы получим to (а7 ) +... + bkNvN (а7) = и, (а7) д (а7) ■

Эти равенства легко записываются в виде следующих матричных тождеств

bv =v	'дМ 0	0       . д(А2) .	.       0 .       0	,1/ =	^(Aj М1(А2) -	■ М1(А„Г
	. 0	о .	■ д(Ч		M/v(\) M/v (^2) ■	■ M/v Ум )^

Вычисляя определитель от левой и правой частей, получаем, что det(5) = Res(flzf2;g).                                   (5)

Сформулируем теперь теорему, грубо описывающую предельный спектр как подмножество некоторого одномерного полуалгебраического множества.

Теорема 2. Пусть h f^ = hakZk, k=-r

Q (z, A) = z^k (a (z) - A), Q, (x, у, A) = Re (Q (x + iy , A)), Q, (x, у, A) = Im (Q (x + iy , A)),

>4(z_lzz_2Zy_zA) = Res^ (x_zy_zA)_zQ₂ (x,y,A);g = u - z^ -z^.

Тогда предельный спектр содержится в следующем полуалгебраическом множестве решений следующей системы уравнений и неравенств:

Resp(z1,z2,u,A);>4'(z1,z2,u,A)) = 0,Im(z1) = 0,Im(z2) = 0,Im(u) = 0,Re(t/)>0.      (6)

Доказательство. Подробное доказательство теоремы достаточно громоздко. Ограничимся лишь схемой доказательства. Заметим, что надо всего лишь проверить, что если для точки А комплексной плоскости выполняются условия теоремы 1, то для неё обязательно выполняется и условие (6). Этот факт проверяется просто с использованием приведённого выше определения результанта. На самом деле можно немного усилить доказываемый результат и показать, что условие (6) описывает одномерное вещественное полуалгебраическое множество.

Опишем теперь точно предельный спектр. Для простоты ограничимся частным случаем г + h =3 и z_x (A),z₂ (A),z₃ (А) — корни многочлена Q(z,A).

Введём следующие обозначения. Пусть U = {А: Res (/I (А, и), 4; (А,и)) = о}, (A                                    Понятно, что А/. = fА:о. (А) = а, (А) = о,(А)). Множество

U \ Ц распадается на два непересекающихся замкнутых подмножества I/ = fА:о, (А) = а, (А) <а,(А)1 и I/, = fА: а, (А) <а, (А) = а,(А)1. Тогда множество U,uV₂ и будет совпадать с искомым предельным спектром. Таким образом, получаем следующую теорему.

Теорема 3. Предельный спектр совпадает со следующим полуалгебраическим множеством:

о.ууи^.                      (7)

Замечание. Нетрудно видеть, что, по существу, условие (7) даёт алгоритм нахождения предельного спектра, поскольку каждое из множеств, входящих в (7) допускает алгоритмически эффективное описание в терминах обычных результантов, так как наличие у многочлена f корня кратности, не меньшей чем к, может быть записано в виде условия: Res^f (x),/^rl,

(х)) = 0. То есть, каждое из множеств, входящих в условие (7) является алгебраическим и эффективно описывается как множество нулей многочлена, а разность алгебраических множеств, как известно, является полуалгебраическим множеством. Следовательно, полуалгебраическим множеством является и всё множество, описываемое условием (7). Последнее также влечёт возможность алгоритмического описания данного множества.

Пример вычисления предельного спектра.

Возьмём многочлен: a(z) = z ¹ + z. В этом случае, получающиеся матрицы являются самосопряжёнными и спектр их, а следовательно и предельный спектр, будет вещественным.

Вычислим <2(z,A): Q(z,A) = z(a(z)-A) = z(z ¹ + z - А) = 1- Az + z².

Полученный результат преобразуем к виду Q_x (х,у,А) + iQ₂ (х,у,Х):

Qi(x,y,X^ + iQ₂^x,y,X^ = l-Xx-iXy + x² + 2ixy-y² = 1-Ах + х² -у² + /(-Ау+2ху), Q, (х,у,Х) = 1 - Ах + х² - у², <2₂ (х,у,А) = -Ах + 2ху

Обозначим многочлены Q1(x,y,X),Q2(x,y,X), через ^ и f2, соответственно, а также рассмот- рим многочлен

и, таким образом, имеем три многочлена:

Будем выполнять разложение многочленов по базису: М = {1,х,у,у²}.

Выразим: х² =/j + у² + Ах-1, ху = ^f₂ +^у, тогда д(и,х,у) = и-х²-у²

= (/ - /j - 2у2 - Ах +1.

Вычислим:

хд = xu - xf, - 2ху²

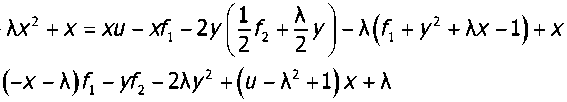
yg = yu -yfx- 2у3 - Хху + у;

Составим матрицу из остатков:

	д	хд	уд	угд
1	(ц+1)	А	0	0
X	-А	(и - А2 +1)	0	0
У	0	0	(ц-1)	0
У2	-2	-2А	0	(ц-1)

Вычисляя определитель матрицы, получаем:

А(х,у,и,Х) = -2u⁷ +и⁴ -иХ⁷ +2и⁷Х⁷ -и³Х⁷ +1.

Если вычислить А^ (х,у,и,Х)

А' (х,у,и,Х) = -4и + 4и³ -А² +4иХ² -Зи²Х².

Тогда, Res(A(x,y,u,Ky,A^ (x,y,u,X^ = 0, поскольку у многочлена А^х,у,и,Х^ и его производной есть общий корень -1. Следует исключить этот корень и опять использовать условие равенства нулю результанта. Но проще сразу найти условие кратности корней многочлена А^х,у,и,Х^ ■ Таким образом, исключая кратный корень [и =1], получим корни:

1 Л2 -1 +1VA4-4A2,- А2 -1 - - УА4 -4А2.

2        2           2        2

Можно было сразу найти разложение результанта, получив искомые корни, что быстро даёт ре^ шение задачи:

t;⁴ - u³X² + 2и² (А² -1)-(/А² +1 = 0

solve for u

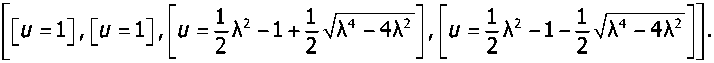
Мы видим, что в силу условий (6) А может быть любым вещественным числом. Далее необходимо использовать условия, описывающие множество Ц (то есть, по существу, (7)), но проще использовать условие наличия лишь двух вещественных корней. Осталось заметить, что третий и четвёртый корни обязаны быть комплексными, то есть должно выполняться условие: А2 - 4 < 0.

Исходя из этого, можно сделать вывод о том, что точка А является точкой предельного спектра в том и только в том случае, когда А е [-2; 2]. Таким образом, предельный спектр в этом случае совпадает с отрезком [-2; 2].

Данный результат можно подтвердить следующими рассуждениями. Так как Q(z,A) = z(a(z)-A) = z(z ¹ - А + z) = l- Xz + z², то многочлен Q(z,X) имеет следующие корни:

• /.. А ± VA² - 4 ..                ~

zx 2 (А) =---------. Модули корней совпадают в том и только в том случае, когда дискриминант отрицателен, то есть когда |А| < 2 или -2 < А < 2.

Заключение. Данная работа содержит промежуточные результаты. В частном случае рассматривается алгоритм, дающий описание предельного спектра. В общем случае описание такого алгоритма становится более громоздким. Наличие алгоритма, дающего точное (а не приближённое), описание предельного спектра представляет несомненный теоретический интерес. Возникают естественные вопросы о скорости работы такого алгоритма, о его практической применимости и эффективности. В дальнейшем планируется вернуться к рассмотрению этих вопросов. Интересным, хотя и весьма сложным, вопросом является также обобщение теоремы 2 данной работы на другие классы тёплицевых несамосопряжённых матриц [7]. Сложность такого рода результата понятна в силу того, что он должен включать в себя теоремы типа слабой теоремы Сегё для этих классов несамосопряжённых тёплицевых матриц.