Об определении неоднородных реологических свойств балок

Введение. Материалы со сложными, в том числе неоднородными механическими свойствами [1-3] (полимер- и пьезокомпозиты, функционально-градиентные материалы и т.д.), широко распространены в различных отраслях (точное машиностроение, авиастроение, измерительная техника, биоинженерия и т.д.). Поэтому при производстве элементов конструкций из таких материалов и контроле качества их изготовления определение законов изменения теплофизических и механических свойств является весьма важной и актуальной задачей. Традиционные экспериментальные методы оценки реологических свойств таких материалов в рамках гипотезы однородности являются достаточно грубыми, следовательно, необходима разработка альтернативных неразрушающих методов идентификации неоднородных характеристик, позволяющая уточнить структуру неоднородности.

Предложенный метод исследования основан на аппарате обратных коэффициентных задач в механике деформируемого твердого тела и позволяет восстанавливать неизвестные одномерные функции по данным акустического зондирования, измеренным в некоторых точках исследуемого объекта [4]. Описание реологических свойств, как правило, осуществляется по модели стандартного вязкоупругого тела и ее обобщения на неоднородные материалы. В данной работе рассмотрен ряд задач о восстановлении комплексной функции, характеризующей неоднородные вязкоупругие свойства стержня при возбуждении изгибных колебаний для различных способов нагружения. Рассматриваемые задачи решаются с помощью итерационного алгоритма, основанного на аппарате интегральных уравнений Фредгольма 1-го и 2-го рода. Постановка задачи и построение общей схемы исследования. Исследуется задача об изгибных колебаниях неоднородной вязкоупругой балки длиной l при различных способах возбуждения колебаний. Неоднородность механических свойств моделируется зависимостью мгновенного и длительного модулей упругости от продольной координаты x .

Уравнение установившихся колебаний в безразмерном виде после отделения временного множителя будет иметь вид [5]:

^f . d² w ( x , к ) )     4

G ( x , i ^к) 71--^к w ( x , ^к) = q ,

(             dx ²    J

. . i тк д ( x ) + h ( x ) где G ( x , i к ) =—   ——

1 + i тк

– неизвестная функция, характеризующая неоднородные реологи- ческие свойства, E(x) = H(0)g(x), H(x) = H(0)h(x) - мгновенный и длительный модули упругости соответственно, которые могут быть как гладкими положительными функциями, так и иметь конечное число разрывов первого рода (что моделирует слоистые структуры).

. „                            4 Р® Fl ⁴ _c JH (0)

Здесь также введены параметры: к = ^^^ - безразмерная частота и т = n J — 4^- -безразмерное время релаксации.

Для уравнения (1) рассмотрены три задачи, отличающиеся как способом нагружения, так и дополнительной информацией, используемой для процедуры идентификации.

Граничные условия для различных способов нагружения можно представить в следующей форме:

• 1)    w(0, к) = 0, w'(0, к) = 0, G(1, iк)w"(1, к) = 0, (G(1, iк)w"(1, к))' = 1

для консольно закрепленной балки, нагруженной на свободном конце сосредоточенной силой при отсутствии поперечной нагрузки ( q = 0 );

• 2)    w(0, к) = 0, w'(0, к) = 0, G(1, iк)w"(1, к) = 1, (G(1, iк)w"(1, к))' = 0

для консольно закрепленной балки, нагруженной на свободном конце сосредоточенным моментом при отсутствии поперечной нагрузки ( q = 0 );

• 3)    w0, к) = 0, w(1, к) = 0, w"(0, к) = 0, w"(1, к) = 0

для шарнирно опертой балки, нагруженной сосредоточенной силой q = q ₀ 8 ( x - x ₀) .

Соответствующие краевые задачи при заданных законах неоднородности могут быть решены лишь численно. Для этого был использован метод предварительного сведения к интегральному уравнению Фредгольма второго рода. Введем вспомогательную функцию v ( x ) сле-

,z x         . x d ² w ( x , к )

.

дующим образом: v(x,к) = G(x,iк)----—- dx2

Перейдем от исходного уравнения (1) к системе уравнений второго порядка относительно функций w и v c соответствующими граничными условиями:

d ² w ( x , к ) _ v ( x , к )

dx ²

d ² v ( x , к ) dx ²

G ( x , i к ),

= к ⁴ w ( x , к ) + q .

Интегрируя уравнения (5) два раза по переменной x , получаем:

^{w ( x} , ^{к )} = j ^{( x -} У ⁽ ^   ^d ^ ⁺ A 1 ^{x +} A 2 ,

• ^J₀       ^G & i ^{к )}

  
  

• v ( x , к ) = к ⁴ j ( x - ^ ) w ( ^ , к ) d ^ + q + B 1 x + B ₂.

Константы A 1 , A ₂ , B 1 , B ₂ находим из граничных условий (2)-(4). Подставляя выражение для функции v ( x ) и меняя порядок интегрирования, получаем интегральное уравнение Фредгольма второго рода для определения функции w ( x , к ) :

1 w ( x , к ) = к ⁴ j w ( п , к ) K ( x , n ) d П + f ( x , к ) .                          (7)

В зависимости от граничных условий, ядро и правая часть имеют различный вид; для упругого случая этот вид представлен в работе [6].

Для решения интегрального уравнения (7) использован метод коллокаций [7], с помощью которого задача сведена к решению линейной алгебраической системы относительно узловых неизвестных. На основе такого подхода проведен ряд вычислительных экспериментов по решению прямой задачи для различных способов нагружения (2)-(4) и различных типов неоднородности; получены необходимые для решения обратной задачи амплитудно-частотные зависимости.

При постановке обратной задачи считаем известной дополнительную информацию в некотором частотном диапазоне [ к 1 , к ₂] : 1) о функции смещения свободного конца балки w (1, к ) = f ( к ) ; 2) об угле поворота свободного конца w ‘ (1, к ) = f ₂( к ) ; 3) о функции смещения в точке приложения нагрузки x ₀ е [0,1] w ( x ₀, к ) = f ₃( к ) .

Сформулированные математические задачи на основе (1)-(4) об определении комплекснозначной функции G ( x , I k ) по описанной дополнительной информации представляют собой нестандартные обратные коэффициентные задачи, являются нелинейными и некорректными проблемами и при их решении необходимо использовать регуляризованные подходы. Нестандартность изучаемых обратных задач состоит в том, что требуется определять комплексные функции координаты по заданной комплексной функции частоты колебаний; существующие современные способы анализа подобных задач существенно зависят от вещественности определяемых функций [4].

Для построения комплексных операторных соотношений, которые связывают искомую и заданную функции, рассмотрим слабую постановку задачи. Пусть v ( x , к ) = w ( x , к ) - гладкая функция, сопряженная к w ( x , к ) [8]. Умножим ее на уравнение (1) и проинтегрируем полученное равенство по отрезку [0, 1]. Далее, осуществляя интегрирование по частям и используя граничные условия, получаем общее нелинейное операторное уравнение, связывающее функции G ( x , i к ), w ( x , к ) , f ( к ) , где ке [ к 1 , к ₂] :

J ( G ( x , i к ) w "( x , к ) w "( x , к ) - к ⁴ w ( x , к ) w ( x , k ))dx = f ( к ) .                   (8)

Пусть известно некоторое начальное приближение G ₀( x , i к ) решения уравнения (8).

Осуществим процедуру линеаризации [9], представив функции в виде g (x, i к) = g 0 (x, i к) + eg 1 (x, i к), h (x, i к) = h 0 (x, i к) + e h (x, i к),

G ( x , i к ) = G ₀ ( x , i к ) + e G 1 ( x , i к ), w ( x , к ) = w ₀ ( x , к ) + e w 1 ( x , к ) , где ε – формальный параметр.

Собирая слагаемые при одинаковых степенях ε и интегрируя полученные равенства по частям с сохранением главного по порядку слагаемого, получаем:

J G 1 ⁽ x , z k ) w 5( x , ^к ) w 5( x , K )d^x = f ^{( к )} - f ₎( ^к ), ^{ке [ к} 1 , ^к 2 ^] ,                      (9)

• 1                                                                                                                          ______________

где J [ G c ( x , i к ) w 0 ( x , к ) w 0'(1, к ) -к ⁴ w e ( x , к ) w 0 (1, к )] dx = f ₃ ( к ) .

Таким образом, сформулировано комплексное операторное соотношение (9), связывающее заданные и искомые поправки. Полученное уравнение является интегральным уравнением Фредгольма первого рода с гладким ядром относительно неизвестных функций первого приближения.

Отделяя вещественную и мнимую части для функции первого приближения комплексного модуля, получаем из интегрального уравнения (9) систему вещественных уравнений:

f 1

f ⁽ g i ^{( x} ) z 2 ( ^к ) + h i ^{( x} ) z i (k^ ⁽ x, к ) ^ ⁽ x , K )d^x = Re f ( к ) - ^f 0 ( к )),

<

f ⁽ 5 i ⁽ x ) ^- h i ^{( x )}> з ^{( к )} м 0 ⁽ x ^{к ) и (} x K dx = Im f ^{( к ) -} f о ^{( к ))},

!i a a a           o Q        z x 1           z x     T2 к4                  тк2

где введены обозначения z_x ( к ) =--- —, z ₂ ( к ) =--- —-, z ₃ ( к ) =--- —.

• ¹       1 + т ² к ^{4     2}       1 + т ² к ^{4     3}       1 + т ² к ⁴

На основе системы операторных соотношений (10) может быть построен итерационный процесс уточнения неизвестных функций, основанный на приближенном решении уравнений (10) с помощью метода регуляризации А. Н. Тихонова [10].

В соответствии с этим для различных типов граничных условий i -й шаг итерационного процесса описывается следующими операторными уравнениями:

' 1

"

"

f ⁽ g i* ^{( x )} z 2 ^{( к ) +} h i* ^{( x )} Х ^(кМ ^{( x}, ^{к )} и о^{1 (} X, ^к )d^x = Re( f ^{( к ) - fi} о ^{( к} )),

0                                      ____________ г i i                   i "             i"

f ⁽ g i ^{( x ) -} h i ^{( x )) z} з ^{( к ) И} о ^{( x} , ^{к ) и} о ^{( x} , K dx = ^{Im( f ( к ) -} / о ^{( к )}Х

. о

причем h о¹⁺¹ ( x ) = h о¹ ( x ) + h i¹ ( x ) , g о‘⁺¹ ( x ) = g о‘ ( x ) + g i‘ ( x ) .

Начальное приближение G ₀( x , i к ) построено в классе линейных комплексных ограниченных функций, коэффициенты которых определены из условия минимума функционала невязки:

^к 2

Ф = f| и ⁽ X о , ^{к ) -} f ^{( к})| d ^к , ^к 1

на некотором компактном множестве в четырехмерном пространстве, где и ( x _о, к ) - функция смещения в заданной точке стержня при некотором законе изменения комплексного модуля. Процедура минимизации функционала невязки осуществлена с использованием эволюционного алгоритма [11]. На каждом шаге построенного процесса посредством решения интегрального уравнения Фредгольма второго рода было найдено новое значение и о , с помощью которого вычислена правая часть интегрального уравнения Фредгольма первого рода и его ядро в уравнениях (11). Результатом решения этого уравнения стала поправка к неизвестной функции, и с ее учетом был проведен следующий этап итерационного процесса; процесс останавливался при достижении необходимой точности в функционале (12).

Численные результаты исследования. На основе предложенной схемы исследования для различных типов краевых задач по заданной амплитудно-частотной характеристике проведена серия вычислительных экспериментов по восстановлению функций g ( x ), h ( x ) , характеризующих законы изменения мгновенного и длительного модулей. Расчеты проведены для стержня из вязкоупругого материала в случае монотонных и немонотонных законов изменения реологических свойств [7, 11, 12].

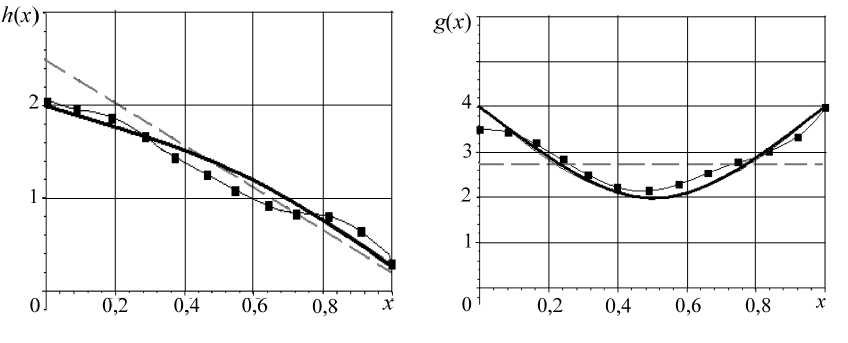
Для краевой задачи (1), (2): h ( x ) = 3 - e^x , g ( x ) = 2cos( n ( x + о,5)) + 4 , начальное приближение h _о ( x ) = о,6 + x , g _о ( x ) = 1,75 x + о,75 .

По рассчитанным амплитудно-частотным характеристикам частотный диапазон выбран следующим образом: [ к 1 ; к ₂] = [2,5; 5,6] .

Для достижения точности 1 - 10 - ⁴ при минимизации функционала (12) потребовалось 42 итерации. Значение параметра регуляризации на последнем шаге: а = 6,1625 - 10 ^{- 6} (см. рису-нок, а ).

а )

б )

в )

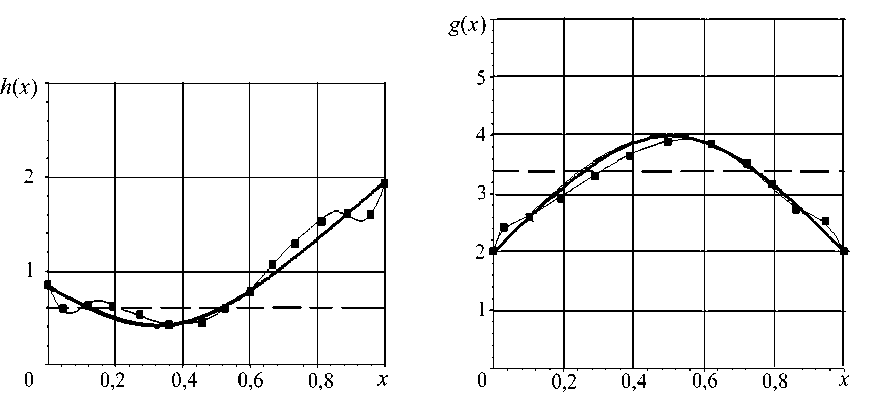
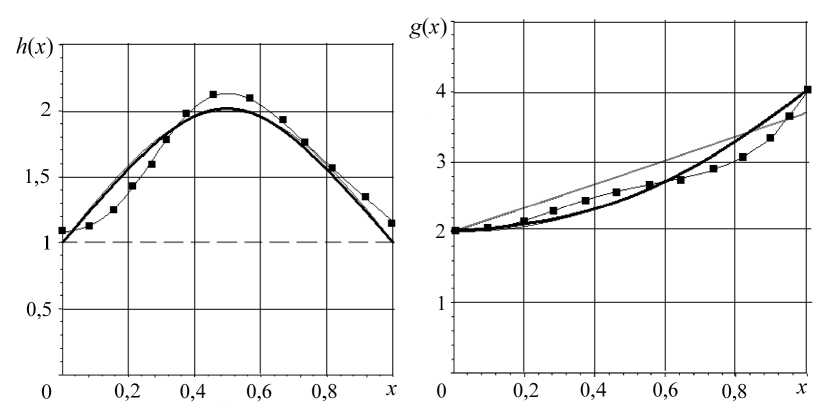
Результат восстановления h ( x ) и g ( x ) :

а – для задачи (1), (2); б – для задачи (1), (3); в – для задачи (1), (4);       – исходная функция;

— - начальное приближение; - ♦ - - восстановленная функция.

Время релаксации т =0,1

Для краевой задачи (1), (3): h ( x ) = 1,4 - cos( n x - 1) , g ( x ) = 2cos( n ( x + 1,5)) + 2 , начальное приближение h ₀( x ) = 0,6 , g ₀( x ) = 3,4 . По рассчитанным амплитудно-частотным характеристикам частотный диапазон выбран следующим образом: [ к 1 ; к ₂] = [3;5,5] . Для достижения точности 1 -10 ^{- 4} при минимизации функционала (12) потребовалось 32 итерации. Значение параметра регуляризации на последнем шаге: а = 3,9812 - 10 ^{- 6} (см. рисунок, б).

Для краевой задачи (1), (4): x ₀ = 0,25 , h ( x ) = 1 + cos(( x + 1,5)л) , g ( x ) = 2 + 2 x ² , начальное приближение h ₀( x ) = 1 , g ₀( x ) = 1,7 x + 2 , частотный диапазон [ к 1 ; к ₂] = [4,4; 7,6] . Для достижения точности 1 - 10 - 4 в функционале (9) потребовалось 20 итераций. Значение параметра регуляризации на последнем шаге: а = 1,4946 - 10 ^{- 5} (см. рисунок, в ).

Выводы. На основе сформулированной строгой постановки обратной задачи для дифференциального оператора четвертого порядка с помощью анализа колебаний балки решена задача об определении функций, характеризующих неоднородные реологические свойства материала. Представлены операторные соотношения, связывающие искомые и заданные функции при анализе установившихся колебаний. Получено решение поставленной задачи на основе итерационного процесса, сочетающего на каждом шаге решение прямой задачи и определение поправок на основе решения интегрального уравнения Фредгольма первого рода с гладким ядром. Представлены примеры определения реологических свойств для различных законов изменения комплексного модуля по длине стержня (экспоненциальных и немонотонных), для различных типов граничных условий. Для монотонных законов максимальная погрешность реконструкции не превышает 5%, а для немонотонных законов максимальная погрешность реконструкции достигает 15%, причем максимальное отклонение восстановленной функции от точного решения наблюдалось на незакрепленном конце в задачах (1), (2) и (1), (3) , и в точке приложения нагрузки в задачах (1), (4). Представленные численные результаты определения неизвестных функций по данным частотного зондирования, основанные на формулировке итерационного процесса, позволяют говорить о работоспособности предложенного метода в достаточно большой серии вычислительных экспериментов.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант №10-01-00194-а), ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (госконтракт П596) и Южного математического института (Владикавказ).