Об определении потребной конфигурации беспилотного летательного аппарата с изменяемой структурой

В настоящее время ведутся работы по исследованию повышения маневренности летательных аппаратов. В качестве объекта исследования выступает летательный аппарат, выполненный по нормальной схеме с неподвижным крылом, в зарубежной литературе принят термин «fixed-wing». Рассматривается процесс движения на этапе посадки. В работе [1] такой маневр описывается как парашютирующая посадка. Аппарат во время такого маневра «проваливается» на некоторую высоту, а затем происходит выравнивание и приземление. Нагрузка на шасси в момент касания земли значительная, но при этом удается выйти к точке приземления с минимально возможными горизонтальными и вертикальными скоростями. Выполнение маневра парашютирующей посадки без существенных повреждений летательного аппарата осуществляется летчиками высокой квалификации.

В работах [2, 3] принят термин «perched landing» дословно означающий «посадка на жердочку», так авторы обозначают посадку на некоторую опору таким образом, что в момент непосредственно приземления вертикальная и горизонтальная скорости движения аппарата равны нулю или близки к ней. Это определение близко по смыслу к парашютирующей посадке и можно говорить об эквивалентном использовании терминов. Заключительным этапом маневра, в зарубежной литературе получившим название «post stall», парашютирующей посадки является гашение вертикальной и горизонтальной скоростей путем вывода аппарата на критические и закритические углы атаки. При этом значительно возрастает сила сопротивления и падает подъемная сила крыла, однако устойчивое движение на этих режимах возможно, о чем свидетельствуют исследования, опубликованные в работах [3, 4].

Существует несколько подходов для математического описания процесса выполнения парашютирующей посадки. Первый уровень сложности – это идеальное представление процесса, когда летательный аппарат представляется материальной точкой, движущейся под действием аэродинамических и инерционных сил [2]. На этом уровне представления автор не предлагает технического решения, позволяющего обеспечить требуемый маневр.

На втором уровне сложности используются математические модели, описывающие движение летательного аппарата как твердого тела [3, 4]. Так же как и на предыдущем уровне сложности, математическое представление коэффициентов подъемной силы и силы сопротивления представлены зависимостью от угла атаки а в следующем виде:

С y = sin 2 а ;

C x = |sin а|.

Первые два уровня дают общее представление о поведении летательного аппарата на этапе парашютирующей посадки и хорошо согласуются с экспериментом [4].

Одна из главных проблем, с которой приходится сталкиваться на этапе взлета или посадки, это малые скорости полета. На скоростях, близких к критическим, аэродинамические органы управления мало эффективны, в этом случае есть возможность использовать внутреннюю энергию. Используя закон сохранения кинетического момента можно обеспечить управление БПЛА. Изменяемая в полете структура реализуется путем взаимодействия взаимосвязанных платформы и подвижного груза. Платформа – это основная аэродинамическая поверхность аппарата, которая может быть выполнена по любой из существующих аэродинамических схем. Груз – это элемент аппарата, имеющий некоторые степени свободы относительно платформы. Изменение конфигурации БПЛА осуществляться следующим образом: платформа связана с грузом шарниром, который дает возможность грузу поворачиваться относительно его, тем самым элементы меняют положение друг относительно друга. Это позволяет управлять суммарным моментом инерции аппарата и его статической устойчивостью. По существу это решение напоминает принцип, используемый в дельтапланах, где пилот изменяет взаимное расположение несущей аэродинамической поверхности – платформы и собственного тела – груза.

В работе анализировалось влияние основных структурных параметров модели (см. таблицу) на поведение беспилотного летательного аппарата:

• •    массы первого (платформа) и второго (груз) звена, m пл и m гр , массу платформы примем постоянной и равной 10 кг, масса груза будет принимать следующие значения: 1 и 2 кг;

• •    величина выноса оси вращения груза относительно центра масс первого звена r₁₂ - r 1 g = r vinCG , влияние выноса оси вращения на динамику движения аппарата неизвестно, поэтому на первом этапе примем следующие значения этой величины для исследования: без выноса, 0,1 и 0,2 м;

• •    величина смещения центра масс груза относительно оси его вращения r₂ g , влияние смещения центра масс второго звена относительно оси его вращения также неизвестно, поэтому на первом этапе примем следующие значения этой величины для исследования: 0,1; 0,2 и 0,3 м;

• •    азимут угла поворота груза относительно продольной оси аппарата ф задавался равным нулю.

Основные структурные параметры модели

Выполнение маневра парашютирующей посадки, а особенно его заключительной части требует большого по величине управляющего момента, например, в работе [3] для этого использовался руль высоты на аппарате, выполненном по нормальной аэродинамической схеме. Однако на скоростях, близких к скорости сваливания, эффективности аэродинамических органов управления недостаточно. В этом случае возможно применение балансирного управления, впервые его использование было описано в работе [6]. Задача исследования динамики движения аппарата с балансирным управлением в механике описана как движение системы твердых тел. Дифференциальные уравнения движения системы твердых тел в приложении к движению автономных транспортных систем, состоящих из двух или более тел, ранее были получены во многих работах, в том числе [7–9]. В наиболее общем виде такие уравнения описаны в работах [10–13] и их можно представить следующим образом:

q = H и;

M (q )U = f (t, q, u) + HT (q) GT (q, t)X;

g (q, t ) = 0, где q - вектор обобщенных координат, используется для определения конфигурации системы нескольких тел в любой момент времени t; M (q) - симметричная положительно определенная матрица массы; f (q, и, t) - функция, представляет собой вклад центробежных сил, сил Кориолиса и условий внешнего воздействия; H (q) - матрица, представляющая собой кинематическую связь между переменной скоростью и, являющейся производной обобщенной координаты q, в виде и = H (q) q. Часто H является тождественным отображением. В случае пространственного движения полное представление более удобно, что позволяет избежать обычных трудностей с представлением особенностей H = HT (HHT) ; g - система алгебраических уравнений, описывающих ограничения, предполагается, что функция дважды непрерывно дифференцируемая; G – Якобиан; X - вектор множителей Лагранжа.

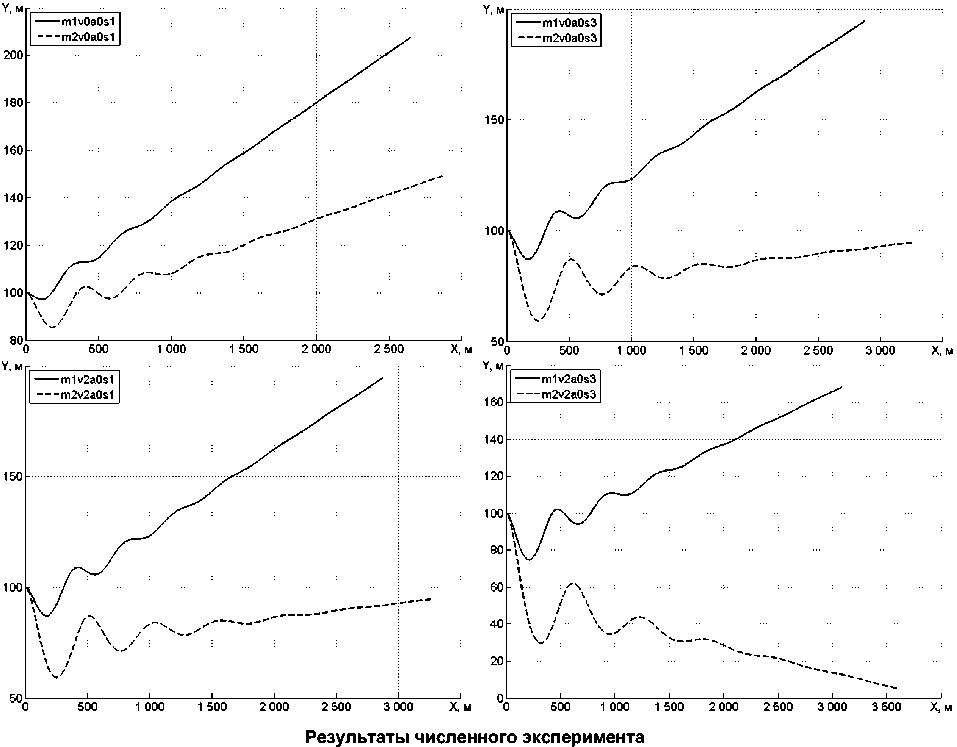
Численный эксперимент проводится для конфигурации аппарата с нулевым азимутом подвижного груза. Задаются начальные условия моделирования: высота полета, начальная скорость полета и соответствующие опыту структурные параметры. В модели реализован закон управления грузом, который удерживал груз в начальном положении, обеспечивая потребный момент, не допуская его отклонения более чем на 5 градусов. Общая схема численного эксперимента представлена в таблице.

Были получены следующие зависимости: профиль полета (см. рисунок), изменение кинематических параметров – ускорение, скорость и обобщенные координаты от времени, а также величины внешних сил, возникающих в ходе движения БПЛА.

Обработка результатов эксперимента велась по профилю полета. Были определены угол наклона траектории и величина ее смещения относительно начального состояния. Выявлены конфигурации БПЛА, при которых изменение центровки приводит к возникновению пикирующего момента, это конфигурации m2v1a0s3, m2v2a0s2 и m2v2a0s3. Это конфигурации с суммарным смещением груза массой 2 кг относительно центра тяжести платформы на 0,4 м. В обозначенных конфигурациях есть возможность осуществлять управление величиной суммарного момента, действующего на БПЛА, путем перемещения подвижного груза на заданную величину. Это дает возможность осуществлять управление летательным аппаратом в условиях низких скоростей. Для того чтобы экспериментально подтвердить исследуемый эффект, значение относительного момента инерции должно лежать в интервале от 1,11 до 1,21 относительных единиц момента инерции, т. е. отнесенных к моменту инерции летательного аппарата без балансировочного груза.