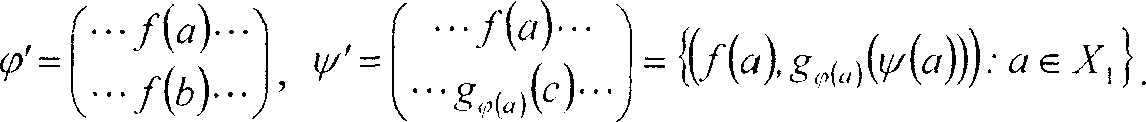Об определяемости упорядоченных автоматов полугруппами их входных сигналов

Под упорядоченным автоматом будем понимать, следуя [1], алгебраическую систему вида А = ^Х,8,У,3,Л), где X- упорядоченное множество состояний автомата, у-упорядоченное множество выходных сигналов, 5 - полугруппа входных сигналов, 5: SxX -> X - функция переходов и Л:8хХ-»У - выходная функция, удовлетворяющие при всех s,s'e S,x е X условиям <5(sx',x) = 3(s' ,d(s,x)); при фиксированном значении 5 отображение З^д^ является эндоморфизмом X, отображение Я(»,х)-гомоморфизмом X в У.

Доказательство предложения 2.1 из [1] без труда переносится на следующий результат.

Лемма 1. Для произвольных упорядоченных множеств X, У алгебраическая система Atm(X,Y) = (x,S,Y,8,2) с полугруппой S = EndX х Нот(х ,У} и функциями 3^cp,ip\x^= ф^, А.^ф,щ\х^ = щ^ является упорядоченным автоматом, который обладает следующим универсальным свойством: для всякого упорядоченного автомата A = (x,S',Y,3,A) существует, и притом единственный, гомоморфизм по входным сигналам этого автомата А в автомат Atm(x,Y).

Автомат Atm(X,Y) называется универсальным упорядоченным автоматом над упорядоченными множествами Х,У

Из работы Л.М. Глускина [2] следует, что полугруппы эндоморфизмов упорядоченных множеств Х,¥ изоморфны в том и только в том случае, если упорядоченное множество X изоморфно упорядоченному множеству Y или двойственному для него упорядоченному множеству у. Это означает, что универсальные упорядоченные автоматы без выходных сигналов вполне определяются своими полугруппами входных сигналов.

Мы распространяем этот результат на универсальные упорядоченные автоматы общего вида.

Теорема. Пусть Х_р У_рХ₂ У₂ - произвольные упорядоченные множества, причем порядок на одном из множеств Х_рХ₂ отличен от тождественного. Тогда для универсальных упорядоченных автоматов Atm(X_pY), Atm(X₂,Y₂) следующие условия эквивалентны:

• 1)    полугруппы входных сигналов автоматов А^ХрУД Atm(X₂,Y₂) изоморфны;

• 2)    упорядоченные множества Х_р Y_t соответственно изоморфны упорядоченным множествам Х₂,У₂ или упорядоченным множествам Х_г,¥_г.

Доказательство теоремы основывается на следующих вспомогательных результатах.

Лемма 2. Одноместный предикат Ф(х) = (VyX,vx = х) теории полугрупп определяет в полугруппе S = EndX х Нот^Х , У) множество всех ее элементов, являющихся парами постоянных отображений множества X в X и X в У соответственно.

Доказательство. Очевидно, что пары постоянных отображений множества X в X и X в У являются правыми нулями полугруппы S. Действительно, если с_а- постоянное отображение множества X в точку а е X и с_ь- постоянное отображение множества X в точку b а У, то для любой пары (ф.ф^еЕ выполняется

(^V/Xca,cA)=(^„,^) = (cu,cJ •

С другой стороны, если преобразование (уху/) является правым нулем полугруппы S, то для любого преобразования (^.^^е S' выполняется условие Ypx-VxXV’T^VP’YY в частности для произвольного элемента а, е X и значений а = ф(а_х), b = ip\.Ui) выполняются равенства

Gw)= к ,с_Ь1 X^.y/j^yx^y/^ (с,„_(О|))с_|;/((,_|))= (с_а,с_ь).

Значит, (уху/) = (с,, с,,).

Лемма 3. Одноместный предикат теории полугрупп Ч^х^ (VyXyy = у) определяет в полугруппе S = EndX х Нот^Х , У) множество пар вида (]_v,^), где 1_Г - тождественное преобразование множества X и у/ е Нот^Х,У\

Доказательство. Для любого у/еНот^Х,У^ упорядоченная пара (l_v,y/) является левой единицей полугруппы 5, так как для любой пары (^.y/JeS выполняется

О V • У7 Хй • У7! ) = О X ^1Д X У7!) = (й . ^ )

С другой стороны, если отображение (у>,у/) является левой единицей полугруппы 5, то для любой пары ^.ip^eS выполняется условие (ф.фХфх’ЧЛ^ (yy.y/J, в частности для пары (l^y/JeS выполняется условие (уху/Х^У⁷^ (l.v.y/J- С другой стороны, имеет место равенство

(у?, у/^д , у/)) = (уйу, У’УА ) = (ух ФУх )•

Следовательно, ф = (\ ^и (уху⁷) ⁼ Ох-У⁷ )•

Обозначим символом U множество левых единиц полугруппы 5, символом Z-множество правых нулей полугруппы S. На множестве правых нулей полугруппы 5 определим отношение эквивалентности е по формуле х = у(х) о (Ve е U Ххе = уе).

Лемма 4. Пусть (с„ , с_ь ), (с_Д| , с₆)- правые нули полугруппы S = EndX х Нот(х,У\ Тогда пара Y_UX,) в том и только в том случае эквивалентна паре (с„ ,с_л ) по отношению г, если а = а_х.

Доказательство. Пусть (с,,,^)^ (с^.С/Дг), где а.а_х е X,b,b_x е У. По определению отношения эквивалентности е для любой пары (l_v,y/)el/ выполняется

(Сг^Хк.У7Мсч>сЛ1л’У7)-

По определению операции в полугруппе S это условие можно записать в виде

Это равенство можно переписать в виде

(с, Ад J4c,

Следовательно, с_и=с_М] и у/(а) =,//(«,). Значит, а = а_х.

С другой стороны, для произвольных а е X, Ь,Ь' е У и (\_x,ip)eU выполняется равенство (с,аЖаЫс,.аХ1.у.У⁷), так как

(с„■ сь Х1 х ■ У7) = k 1 х - СХ^ = к, ■ А( J, с другой стороны,

По определению эквивалентности е это означает, что (с« • ^сь ) - (с, • ^сь' X^е) ■

gd^=" <^ ^«Х^ ксДиУс:кздесъ yeYx,ze Y2).

Тогда справедливы следующие утверждения:

• 1)    отображения f: Х_х -> Х₂ ' и g_u: Y, —> У, (а е Х_х) являются биекциями;

• 2)    для любой пары Ур,ф^е8_х выполняется равенство

где ф'\ф{аУ= g

• 3)    если порядок на одном из множеств X_VX, отличен от тождественного, то определенные выше отображения /: Х_х -> X, и g_u: У, —> Y, (a е X,) являются изоморфизмами упорядоченных множеств X_x.Y_x соответственно на упорядоченные множества X₂,Y₂ или на двойственные им упорядоченные множества x,,Y_b ■

Доказательство. Так как изоморфизм л; S_x = 5Vсохраняет приведенные в леммах 2-4 формулы и конструкции, то индуцируемые отображением л отображения f:X_x^X₂ и g_o:Y_x-^Y₂ (а е A^J будут биекциями.

Так как кс_и,сХфХ^- к^с«Ф>^с2^-(^сгрЩ)-^cT(.:j) , то условие (1) равносильно тому, что (^T_l)'(^y/)=(c„,cJ.

Так как л- изоморфизм полугруппы 5* на 5 , то выполняется равенство ЛфХлХЛфХ^ЛхсУ                 (2)

Обозначим л^р.ф^ U)',ф'У Так как по построению биекций / и gJaeX,)

то равенство (2) можно переписать в виде

Это условие равносильно тому, что р'(/(а)) = f{b} и ф'(/(а)) = g_b(с) = g,„(„)(c).

Если представить преобразования ф,Ч^х матрицами

Л..йг...\ У ...у..Л то из предыдущих рассуждений следует, что преобразования ф' ,ф' будут представлены матрицами:

Обозначим отображение f- : EndX_x -> EndX, символом л, и покажем, что л_х является изоморфизмом этих полугрупп.

Действительно, для любых ф_х,ф_г^8_х выполняется

*|Ы=/4^^)=г'ф^х = U^WlrwV/Чф^/Чфз^ ^WzY •

Значит, по теореме Глускина [2] отображение / является изоморфизмом или антиизоморфизмом упорядоченного множества Х_х = (А'_|,р_|) на упорядоченное множество А", = (АА.р,). Тогда по предположению леммы порядки на множествах Х_х,Х₂ отличны от тождественных отношений на этих множествах, в частности в множестве А^-, найдутся такие различные элементы «„*/?,,, что (a^ijep,.

Предположим, что f - изоморфизм Х_х на А',, и покажем, что в этом случае для любого а е Х_х биекция g„ является изоморфизмом упорядоченного множества Y_x = (У,, 5,) на упорядоченное множество Y, = (У,,б,У

Рассмотрим произвольную пару (х₀, у₀)е ^ и покажем, что отображение Ф, определенное по формуле

I х₀, если (и,а₀^е р_х,

, если \u,a^t р_х является гомоморфизмом Х_х в .

Действительно, пусть (s,t)e р_х. Докажем, что (y/($),y/(z))e 8_Х.

Если (л«₀)е ^ , то в силу транзитивности отношения р_х, (,s',a₀)e р_х и по определению отображения у/, у/(л) = у/(?) = х₀. В силу рефлексивности отношения 8_Х, (y/(s),y/(/))e 8_Х. Если ^s,a^tp_x, то тем более ya_eyp_v Тогда по определению отображения у/, ^(s) = y/(z) = у₀ и в силу рефлексивности отношения 8_Х заключаем, что (y/(.s),y/(f))e 8_Х. Если же (s,n₀)e р_х, У,аУ^р_х, то по определению отображения V, (y/(s),w)) = (^xo-То)-Отсюда, по условию, (y/(s),y/(z))e 8_Х.

Тогда в силу уже доказанного п.1) л(с_а,у/)= (с^),^¹-) и, в частности, Д- е Нот^Х_г,У-,У С другой стороны, по построению для любого хеХ_х выполняется равенство у/" (/(%)) = g_t.(^^^ в частности, при х = а₀,

^ (/(«О )) = go М°0 )) = ga U ) ’ ¹Г {f(b₀ )) = go (И^О )) = go (To ) ■

при х = b_a,

Другими словами, гомоморфизм i/- отображает упорядоченную пару (/(а₀),/(б₀)) в упорядоченную пару (g„(x₀).g„(y₀)). С другой стороны, в силу того, что f - изоморфизм упорядоченного множества X, на упорядоченное множество Х₂ и (а₀, Ь_о) е р_х, выполняется условие (Ж)>Ж))е р.. Тогда, в силу того, что tp‘- - гомоморфизм упорядоченного множества Х₂ на упорядоченное множество У₂, выполняется условие (g„(T_o).g_a(ro))^e ^2 • Значит,g_a - изоморфизм Y, на Y₂.

По аналогии ясно, что если f- антиизоморфизм X, на Х₂, то все отображения g_a(а е X) также будут антиизоморфизмами Y, на Y₂, так как в этом случае условие ^.Ь^е р_х влечет (/(iJ/Mep, и, следовательно, (g^yo^^U^e ^2 ■

Доказательство теоремы.

Очевидно, что если упорядоченные множества X,,Y_x соответственно изоморфны упорядоченным множествам X,, Y₂ или упорядоченным множествам д^г₂ . У, , то полугруппы входных сигналов автоматов А(т^Х_х,У_хУ Atm(X₂,Y₂) изоморфны.

Обратно: пусть д - изоморфизм полугруппы S, входных сигналов автомата

Atm^XpY^ на полугруппу S₂ входных сигналов автомата А:т^Х₂,У₂У тогда из лемм 2-5 следует, что этот изоморфизм л определяется по указанной в лемме 5 формуле некоторыми биекциями /: Х_х -> Х₂, g„: У_х -> У, (а е Х^, которые одновременно являются изоморфизмами или антиизоморфизмами соответствующих упорядоченных множеств.