Об оптимизации упругого элемента протеза стопы
Автор: Осипенко М.А., Няшин Ю.И.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (52) т.15, 2011 года.
Бесплатный доступ
Приведен обзор новых результатов по оптимизации конструкции упругого элемента (УЭ) протеза стопы. Протез моделируется в виде консольно закрепленной многолистовой рессоры. Между листами имеет место контакт с возможным отставанием; задача изгиба поэтому относится к контактным задачам теории балок. Найдена переменная толщина равнонапряженного однолистового УЭ при сильном изгибе. Показано, что такой УЭ имеет эллиптический профиль. Найдены переменные толщины листов равнонапряженного двухлистового УЭ при слабом изгибе для некоторых значений отношения длин листов. Показано, что при неравных длинах листов более длинный лист такого УЭ имеет внутренний шарнир. Доказано, что при дополнительных слабых ограничениях равнонапряженный УЭ может не существовать. Рассмотрен коэффициент использования материала УЭ. Сопоставлены задачи максимизации этого коэффициента и минимизации массы УЭ и выяснено, что связь этих задач не является простой. Обе задачи могут не иметь решений; первая задача может иметь решения, а вторая - не иметь; первая задача может иметь много решений, одно из которых является единственным решением второй.
Протез стопы, упругий элемент, листовая рессора, линейный и нелинейный изгиб, контактная задача, равнонапряженный упругий элемент, коэффициент использования материала, минимизация массы
Короткий адрес: https://sciup.org/146216021
IDR: 146216021 | УДК: 531/534:
Текст научной статьи Об оптимизации упругого элемента протеза стопы
Проектирование и оптимизация протеза стопы являются одним из актуальных направлений протезостроения. Протез стопы должен воспроизводить ряд функций естественной стопы – опорную, функцию амортизации переднего толчка, функцию накопления потенциальной энергии, рессорную (распластывание под действием вертикальных сил), балансировочную (регуляция позы), адаптационную (способность ходьбы по наклонным поверхностям). Протез стопы должен также обладать достаточной прочностью.
Перечисленным требованиям наиболее полно удовлетворяют конструкции, содержащие так называемый упругий элемент (УЭ), который представляет собой консольно закрепленную многолистовую рессору. УЭ может быть стальным. На рис. 1, a показан серийный образец, изготовленный на экспериментальном заводе средств протезирования, г. Реутово, Московская область. Такие протезы сейчас наиболее распространены. Однако более перспективными являются УЭ, изготовленные из легких композиционных материалов. На рис. 1, б показан опытный образец УЭ, изготовленный в Пермском НИИ композиционных материалов из углепластика КМУ-4Л. На рис. 1, в представлен УЭ протеза Carbon Copy , изготовленный фирмой
Няшин Юрий Иванович, д.т.н., профессор, завкафедрой теоретической механики, Пермь


в г
Рис. 1. Разновидности упругого элемента протеза стопы
Ohio Willow Wood Company , США [6]. На рис. 1, г показан УЭ протеза стопы Quantum Foot , изготовленный фирмой Hanger Inter Med , Великобритания.
Такие конструкционно сложные элементы протеза, будучи более эффективными при эксплуатации, требуют применения более новых методов проектирования, в частности, метода математического моделирования, который позволяет также оптимизировать конструкцию протеза стопы. В настоящей статье изложен ряд результатов по оптимизации УЭ протеза стопы, полученных авторами в последние годы. Эти результаты представляют интерес для специалистов в области расчета рессор и общей теории листовых рессор.
Математическая модель УЭ
Простейшая модель УЭ [2, 3, 7] представляет собой пачку N консольно закрепленных балок (листов) одинаковой ширины w , но с различными длинами l 1 ,..., lN и различными переменными толщинами h 1 ( x ),..., hN ( x ) ( x – координата, отсчитываемая вдоль балки) (рис. 2).
В естественном состоянии (без нагрузки) листы являются плоскими и плотно прилегают друг к другу; трение между листами отсутствует. К краю самого длинного листа, перпендикулярно листу, приложена сосредоточенная следящая сила F . Форма изогнутого листа (в равновесии) задается функцией ϕ ( x ), где ϕ – угол между профилями изогнутого и неизогнутого листов (рис. 3). Если лист изогнут, то в точке с координатой x со стороны правой (по отношению к данной точке) части листа на левую действует сосредоточенный момент
M(x) = Ewh3 (x)ϕ′(x)I12,(1)
где E – модуль Юнга. При этом напряжение (единственная существенная компонента σ xx ) на нижней поверхности листа
σ(x) = Eh(x)ϕ′(x)/2.(2)
Оптимальными считаются [1, 5] равнонапряженные УЭ, т.е. удовлетворяющие условию
σn(x) ≡ σ = const, 1 ≤ n ≤ N .(3)
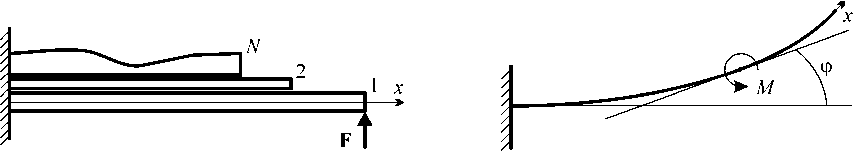
Рис. 3. Схема изгиба одного листа
Рис. 2. Модель упругого элемента
Равнонапряженность может быть достигнута подбором функций hn ( x ) . Рассмотрим вопрос об отыскании этих функций в некоторых частных случаях.
Оптимальный профиль однолистового УЭ при нелинейном изгибе
Пусть УЭ однолистовой. Уравнение равновесия листа следует из (1) с учетом сделанного предположения о нагрузке (сосредоточенная сила):
Ewh 3( x ) ф‘ < x )/12 = F J l cos ( ф ( l ) -ф ( s ) ) ds .
Из (2)-(4) и условия защемления листа (при x = 0) находим ф"/ф'3 = 1 cos (ф(l) -ф), ф(0) = 0, ф'( l) = +w,
где 1 = 3 E 2 F /4 ст 3 w . Нелинейность задачи (5) означает, что рассматривается сильный изгиб. Решение (5) существует (и единственно) при I /1 < 2 и имеет вид
ф ( x ) = arccos ( 1 - l /1) - arccos ( 1 - ( l - x ) /1) . (6)
Тогда из (2), (3) получаем
h ( x ) = ( 2 а1/ E ) ^ 1 - ( 1 - ( l - x )/1 ) 2 , (7)
т.е. однолистовой равнонапряженный УЭ имеет эллиптический профиль.
Практически при нахождении профиля задается не а , а прогиб УЭ l
А = J sin ф ( x ) dx .
Тогда из (6) находим, что l /1 = 1 - cos а , где 0 < а < п - корень уравнения
( sin а-а cos а )/( 1 - cos а ) = 2 А/ 1 . (8)
Легко установить, что при А/ 1 < п/4 это уравнение имеет единственное решение.
Если А/ 1 << 1 (слабый изгиб; эквивалентное условие: |ф( x )| << 1), то из (7), (8)
получаем известный результат [5] - h(x) = 21 (F/EwА)13^/1 - x/l - однолистовой равнонапряженный УЭ при слабом изгибе имеет параболический профиль.
Оптимальные профили двухлистового УЭ при линейном изгибе
Теперь рассмотрим двухлистовой УЭ при слабом изгибе. Предположим, что a) листы УЭ контактируют (кроме точки защемления) только в точке, расположенной на краю более короткого листа; б) а n ( x ) = а (а не модуль, что требуется в (3)). Тогда уравнения равновесия листов УЭ имеют вид
Р Ъ 3(АЧ J- P ( 1 2 - x ) + F ( 1 1 - x ) (0 - x - 1 2 ),
Ewh1( x )ф‘ (x )12 = ^
[ F ( 1 1 - x ) ( l 2 - x - 1 1 ),
Ewh2(x)ф2(x)/12 = P(l2 - x),(10)
Ф1(0) = ф2(0) = 0,(11)
где P – сила взаимодействия листов, которая находится из условия контакта листов в точке x = l 2 :
У1( 12) = У 2( 12);(12)
Уп (x) Iox Фn (5)ds .
Из (9)–(13), (2), (3) (с учетом предположения (б)) можно получить уравнение для P в виде
5 + 2в = (5 + Р)2//1-12, где в = ^ 1 -l2 /11 , 5 = ^ 1 - Pl2 /Fl1 . Легко установить, что при 0 - в < 1 это уравнение имеет единственное решение 5 . Однако находя из (9)-(11), (2), (3) ф1 (x), ф2 (x) и затем из (13) у1(x), у2(x) , можно показать, что при l2 < 11 lim у2(x)/у1(x) < 1 (верхний лист x ^0
«проникает» под нижний), а при l2 = 11 у1(x) ^ у2(x). Таким образом, при l2 = 11 = l получаем одинаковые параболические профили листов h1 (x) = h2 (x) = 21 (F/2EwA)13 71 - x/l, а при 12 < 11 равнонапряженный УЭ, для которого выполняются принятые выше предположения (a) и (б), не существует.
Докажем, что при сохранении предположения (б) при l 2 < 1 1 равнонапряженный УЭ не существует, даже если ослабить предположение (а) и допустить, что листы могут контактировать в произвольном конечном числе точек 0 < xM < ... < x 1 < x 0 = 1 2 < 1 1 . Учитывая, что при 0 - x - xM
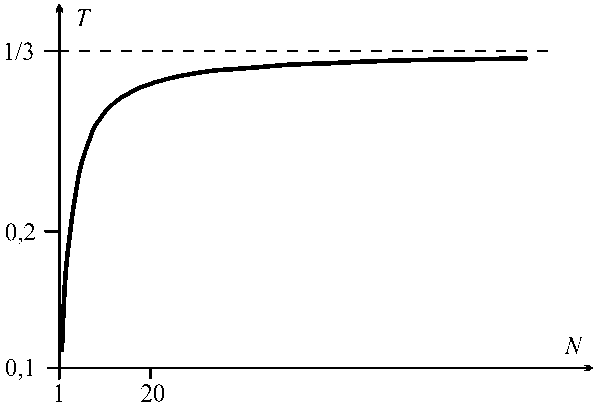
Ewh (x)Ф‘ (x)/12 = F(l1 - x) - X M=0 Pm (xm - x) , Ewh23 (x)Ф2 (x)/12 = ^ M=0 Pm (xm - x) , Ф1(0) = ф2(0) = 0, где Pm – силы взаимодействия листов, получим с учетом (2), (3), (13) из условий Ф1 (xm ) = Ф2 A1 + A2 = A3 + A4, (A1 + 2A2)/(A1 + A2)2 =(A3 + 2A4)/(A3 + A4)2 ,(14) где A1 = F(l1 - xM ) -X M,-1 Pm (xm - xM ) , A2 = Fl, -X M=„ Pmxm ,(15) A3 = VX “-' Pm (■xm - xM ) • A4 = X M=0 Pm '< Из (14)-(16) следует, чтоX M=0Pm = Fl2 и X M=oPmxmll1 = Fl2, но эти два равенства противоречивы, так как Pm > 0 и xm< l1. Поэтому высказанное выше утверждение доказано. Откажемся тогда от предположения (б), сохранив (а). Из (9), (2) следует, что если Pl2 > Fli, (17) то с1(x) меняет знак в точке x* = (Pl2- Fl1)/(P - F). Тогда из (9)-(13), (2), (3) получаем уравнение для P в виде (1 + П)2 = (2-^(П + 3))VП + У/(Y- 1) , где y = 11 /l2, П = ( P/F-y)/(Y -1) • Легко установить, что при y> 1 это уравнение имеет единственное решение п, которому соответствует P, удовлетворяющее условию (17). Тогда профиль нижнего листа 46(P - F)(x* - x)/сw (0 < x < x*), h1 (x) = < V6(P - F)(x - x*)/сw (x*< x< 12), V6 F (/, - x)/сw (12< x< l1). Заметим, что h (x.) = 0; это означает, что в точке x = x. нижний лист имеет 1 * * внутренний шарнир. Профиль верхнего листа параболический: h2 ( x ) = 46 P (12 - x)/сw . Для проверки непротиворечивости предположения (а) и требования равнонапряженности УЭ нужно исследовать знак разности y2(x) - y1(x). Это исследование проводилось численно. Установлено, что y2(x) > y1(x) при Z< 12 /l1< 1, где Z = 2(4-V2)/7, а при 12 /l1< Z существуют 0 < x< 12, для которых y2(x) < y1(x). Тем самым равнонапряженный УЭ с найденными выше профилями существует только при 12 /l1>Z • Вопрос о существовании равнонапряженных двухлистовых УЭ при слабом изгибе для 12 /l1< Z остается открытым и требует дальнейшего исследования. О коэффициенте использования материала УЭ К вопросу об оптимизации УЭ протеза стопы можно подойти и с другой стороны. В литературе [4], [5] качество УЭ характеризуется коэффициентом использования материала (КИМ). Пусть УЭ изготовлен из материала с модулем упругости E и находится в равновесии под некоторой нагрузкой; U – потенциальная энергия упругой деформации УЭ, V - объем УЭ, с max - максимальный модуль главного напряжения в УЭ. Тогда по определению КИМ – это величина T = 2EU V с max Для вычисления КИМ однолистового УЭ обычно используется несколько более общая, чем рассмотренные выше, модель листа. Эта модель показана на рис. 4. Поперечное сечение – зависящая, вообще говоря, от x область D(x) . Главные центральные оси y, z сечения имеют постоянную (не зависящую от x) ориентацию. Изгиб листа происходит в плоскости x z под действием поперечной нагрузки с заданной эпюрой моментов M(x) . Для многолистового УЭ при вычислении КИМ обычно используется модель рис. 2 с листами постоянной толщины. Рис. 4. Модель однолистового упругого элемента, используемая при вычислении В рамках этих моделей можно найти [4], что для однолистового УЭ с произвольным переменным сечением M2(x)dx /', Г Z(X)M(x) T=! ■ /! S(x) dx " amax) где S(x) – площадь сечения, J (x) = Ц z2dyd z D(x) Z (x) = max z I (y, z )eD ( x) Для двухлистового УЭ ц (1 + ц 3) "X 2(3 + X) + 4ц3 "I T =------------------------------ 9(1 + ц-Х){ max"ц2(2 + X),| 2р.3-X |,2X(1 + ц3)" } , 2 где X = 1 -12 //1, ц = h 1 /h2 По отношению к КИМ можно ставить две различные задачи оптимизации. Задача 1. Найти параметры УЭ, для которых T = max. Задача 2. При заданных E, l, M(x) (для двухлистовго УЭ – E, l1, P ) и при условиях f = f0, ^max ^0, где f - прогиб УЭ (f0, а0заданы), найти параметры УЭ, для которых V = min (плотность материала считаем постоянной, поэтому минимизация объема эквивалентна минимизации массы). Можно показать [4], что для решений этих задач справедливы следующие утверждения. Утверждение 1. Для однолистового УЭ с произвольным переменным сечением задача 1 не имеет решения: T< 1 и существует последовательность УЭ, для которой T ^ 1. В этом случае и задача 2 не имеет решения: существует число V такое, что V > V14, и существует последовательность УЭ, для которой (18) выполнены и V ^ V1#. Утверждение 2. Для однолистового УЭ с произвольным постоянным сечением задача 1 не имеет решения: существует число T, такое, что T < T*, и существует последовательность УЭ, для которой T ^ T*. В этом случае и задача 2 не имеет решения: существует число V2* такое, что V > V2#, и существует последовательность УЭ, для которой (18) выполнены и V ^ V2#. Утверждение 3. Для однолистового УЭ с сечением в виде прямоугольника постоянной ширины и произвольной переменной высоты задача 1 имеет неединственное решение: h(x) = const^M(x), причем T = 1/3. В этом случае существование решения задачи 2 зависит от значения величины l x dx =J0 JMto. Если B< да, то задача 2 имеет единственное решение: 2а0BTMx) h(x)=- • 3f2E2 w = —ГТ’ 2^0 B 1 причем V = fl J M (x) dx. ^0 B 0 Если B = да, то задача 2 не имеет решений: существует последовательность УЭ, для которой (18) выполнены и V ^ 0. Утверждение 4. Для двухлистового УЭ задача 1 имеет неединственное решение: 1 = 9/13, ц = 3/2 (неединственность состоит в том, что определяются только отношения I2 /11 и h 1 jh 2 ), причем T = 71/423. В этом случае задача 2 имеет единственное решение: 12 = 41J13, h1 =(142/169)•( 1/ 00 Ef,), h 2 = 2 hj/3, w = (59319/10082 )•( Pf2 E2 /^01/), причем V = (423/71).(Pf0e/a2) . Аналогично результату утверждения 4, можно найти оптимальное значение КИМ для N-листового УЭ с листами постоянного прямоугольного сечения. Соответствующий результат приведен на рис. 5. При больших N величина T близка к значению 1 3, соответствующему однолистовому УЭ параболического профиля. Рис. 5. Зависимость оптимального КИМ от числа листов упругого элемента Заключение Ряд новых результатов оптимизации конструкции УЭ протеза стопы позволяет перейти к проектированию новых нестандартных конструкций. При сильном изгибе следует использовать не параболический, а эллиптический профиль листа. Также можно применить конструкцию с внутренним шарниром. Установлена связь задач максимизации КИМ и минимизации массы УЭ. Эта связь не является простой, что говорит о необходимости с некоторой осторожностью использовать данный коэффициент для оценки оптимальности УЭ.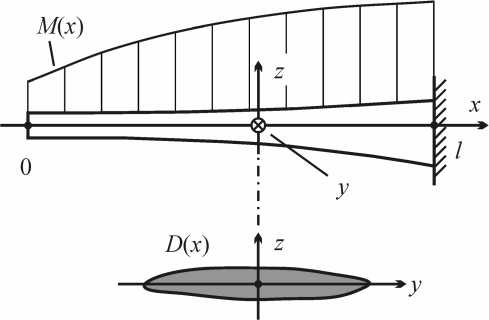
Список литературы Об оптимизации упругого элемента протеза стопы
- Брынских С.И., Осипенко М.А., Няшин Ю.И. Оптимизация двухлистового упругого элемента протеза стопы с использованием линейной и нелинейной теорий изгиба//Российский журнал биомеханики. -2003. -Т. 7, № 2. -С. 9-19.
- Няшин Ю.И., Осипенко М.А., Рудаков Р.Н. К теории изгиба листовой рессоры//Известия РАН. Механика твердого тела. -2002. -№ 6. -С. 134-143.
- Осипенко М.А., Брынских С.И. Отыскание толщин листов равнонапряженных листовых рессор//Вычислительная механика. -Пермь, 2004. -№ 2. -С. 51-54.
- Осипенко М.А., Таланцев Н.Ф. О свойствах коэффициента использования материала листовой рессоры//Изв. вузов. Поволжский регион. Технические науки. -2009. -№ 2(10). -С. 134-144.
- Пархиловский И.Г. Автомобильные листовые рессоры. -М.: Машиностроение, 1978. -227 c.
- Geil M.D., Parnianpour M., Berme N. Significance of nonsagittal power terms in analysis of a dynamic elastic response prosthetic foot//Journal of Biomechanical Engineering. -1999. -Vol. 121. -P. 521-524.
- Osipenko M.A., Nyashin Yu.I., Rudakov R.N. A contact problem in the theory of leaf spring bending//International Journal of Solids and Structures. -2003. -Vol. 40. -P. 3129-3136.


