Об организации параллельных вычислений при решении разностных уравнений

Появление параллельных вычислений приводит, во-первых, к необходимости их широкого освоения, во-вторых к пересмотру ряда базовых понятий вычислительной математики – например, понятия экономичности вычислительного алгоритма. Действительно, параллельные (одновременные) вычисления при их реализации переносят фокус внимания вычислителя с вопроса о минимизации выполняемых арифметических действий на вопрос минимизации времени выполнения алгоритма. В случае выполнения вычислений на одноядерном процессоре решение этих вопросов эквивалентно, для многопроцессорного компьютера или многоядерного процессора компьютера – нет. Для многопроцессорной вычислительной установки или компьютерного кластера возникает дополнительная задача динамической настройки программы / алгоритма на конфигурацию параллельного вычислителя – количество процессоров, их производительность, латентность, пропускную способность коммуникационных каналов. Важен и выбор технологии реализации параллельного алгоритма - MPI, Open MP и др. В 1978 г. появилась статья [1], где поднимался вопрос об организации параллельных вычислений при реализации численных методов решения ряда задач математической физики. И до появления [1] вопрос об организации параллельных вычислений широко обсуждался в научной печати как прикладными математиками – вычислителями, так и разработчиками компьютерных систем. Однако в [1] рассматривался вопрос о распараллеливании строго последовательного алгоритма – метода прогонки – обращения трехдиагональной матрицы. На освоении и численной реализации этого последовательного алгоритма – метода прогонки выросло не одно поколение отечественных прикладных математиков – вычислителей. Отметим как важное обстоятельство и то, что предлагаемый способ распараллеливания не выводил в целом из класса используемых алгоритмов и описывался в терминах, хорошо знакомых прикладным математикам – вычислителям. В настоящее время реализация вычислений по [1] в среде вычислителей известна как «параллельная прогонка Яненко».

Описание алгоритма распараллеливания решения трехточечного разностного уравнения

Приведем описание параллельной прогонки Яненко ввиду ограниченной доступности статьи [1] в настоящее время.

Основная идея параллельной прогонки Яненко состоит в выделении части искомых неизвестных в качестве параметрических (обозначаемых далее через {а к } ), построении системы уравнений относительно {а к } , называемой далее « модулем обмена », определении параметрических неизвестных {а к } и нахождении по ним остальных искомых неизвестных. При численной реализации такого подхода оказывается возможным организовать параллельные (одновременные) вычисления. Для построения модуля обмена необходимо найти зависимость искомых неизвестных от {а к } . Найденные зависимости будем называть « предрешением задачи », так как знание их явного вида и известные значения {а к } решают задачу обращения трехдиагональной матрицы. Узлы сетки, в которых значения искомых неизвестных принимаются за параметрические, будем называть далее « узлами распараллеливания ».

Пусть отрезок (0,1) разбит M точками на M + 1 подинтервал, а каждый подинтервал в свою очередь разбит на N + 1 интервалов. На (0,1) требуется решить разностную краевую задачу:

Л и = ( au_x ) - bu = f ( x ), u ( 0 ) = ^ , u ( 1 ) = ^           (1)

В качестве параметрических неизвестных {а к }, к = 1, M возьмем значения искомой сеточной функции в M точках разбиения отрезка (0,1), то есть примем эти точки за узлы распараллеливания. Для коэффициентов и правой части на к -ом интервале примем обозначения:

k ai = a (к-1) n+i bi = b (к-1) n+i, i = 1,

...

, N , k = 1,.. M .

Значение правой части f и коэффициента b в к -том узле распараллеливания обозначим через Ф к , Ь к . Для построения модуля обмена запишем разностное уравнение в к -той точке распараллеливания

a

к + 1

и 1 ^{+ 1} - а_к h

_п к « к ^- u N - 1

aN

h

- ьк«к

-Ф к , к = 1,..M ,

где u k ^{+ 1}, u k J- значения искомой функции в узлах, соседних с к- тым узлом распараллеливания.

Так как uk+1, ukN_x зависят соответственно только от а ,Щ+1 и ак-^а , то матрица коэффициентов системы линейных уравнений относительно {ak}, к = 1, M будет также трехдиагональной. Найдем её явный вид. Для этого нам необходима параметрическая зависимость uk+1, uk_Y от а, а+j, а-j, а• В силу линейности исходной задачи искомое решение и на к-том подинтервале представимо в виде:

ui = ак -1u10 + аки 01 + u 00, где u\0, uiр u^ - решение следующих краевых задач:

Лku = 0, и0 = 1, uN = 0,(5)

Лки = 0, и0 = 0, uN = 1,(6)

Ли = f, и0 = 0, uN = 0

соответственно. В (5) , (6) , (7) разностный оператор определяется разностным уравнением, рассматриваемым во внутренних точках к- го подинтервала распараллеливания. Задачи (5) , (6) , (7) могут решаться независимо друг от друга и запоминаться в памяти компьютера. Теперь по (4) находим:

+1       ku1'Ч         ku1'Ч    kuk'Ч

u1   = ak (u10 )1 + ak+1(u 01 )1 + (u00 )1, uN-1 = ak—1(^0) N-1 + ak (u01)N-1 + (u00) N-1

Подставляя (8), (9) в (3) приходим к системе уравнений для определения параметрических неизвестных { а } :

a*k ⁺¹

^{( u} 01 ) 1 ^a k + 1

—

[(1 - ( u ^ a k ⁺¹

^{+ (1  ( u} 01 ) N - 1 ) a N ^^ак ⁺ a N ^{( u} 10 ) N-1 ^a k - 1

h

—

b k « k

—

_ k +1/ , k +1\ a 1    ^{( u} 00 ) 1

—

a N ^{( u} 00 ) N - 1

h

—

Ф*, k = 1,..M .

К (10) нужно присоединить краевые условия для {a k } :

^а 0 = М 0^{, а} м + 1 = М 1

вытекающие очевидным образом из (1) . Определив прогонкой {a k }, к = 1 ...M из (10) с краевыми условиями (11) , найдем значения искомой функции и на всем интервале (0,1) c помощью представления (4) . После нахождения {a k }, k = 1, M, вычисление и на каждом подинтервале можно проводить независимо от остальных подинтервалов. Следовательно, параллельные (одновременные) вычисления можно выполнять на этапе предрешения задачи и этапе расчета искомого решения на каждом подинтервале.

Представляет интерес вопрос об устойчивости прогонки для определения {a k }, к = 1, M , Этот вопрос был положительно решен в [2]. В работе была доказана устойчивость прогонки для определения {a k }, k = 1, M как следствие устойчивости прогонки для исходной задачи.

Нетрудно видеть, что подход, предложенный в [1] допускает распространение и на ряд алгоритмов, «родственных» алгоритму обращения трехдиагональной матрицы – далее это было выполнено в [3].

Интересно отметить, что идея параллельной прогонки Яненко возникла в результате обсуждения покойным академиком Н.Н.Яненко с одним из соавторов работы [1] вопроса, касающегося использования для распараллеливания расчетов «точных» разностных схем Тихонова, Самарского [4], см. также [5]. Действительно, если бы разностная схема обладала бы свойством, таким, что решение на грубой сетке одновременно являлось бы решением и на мелкой сетке, то эта разностная схема идеально подходила бы для распараллеливания исходной задачи, хотя бы для одномерного случая. Именно таким свойством обладает модуль обмена – разностная схема для параметрических неизвестных {a k } относительно исходной задачи, инкапсулируя информацию о мелкой сетке во вспомогательных решениях и оо , u io ,u oi .

Описание алгоритма распараллеливания решения двухточечного разностного уравнения

При численном решении ряда задач математической физики, а именно для гиперболических уравнений, широко используются разностные схемы, приводящие, в конечном счете, к реализации последовательных вычислений для двухточечного разностного уравнения. Представляет, на наш взгляд, рассмотреть возможность реализации параллельных вычислений и в этом случае. Рассмотрим двухточечное скалярное разностное уравнение:

P j + i x j + i - Q j x j = f j + i ^,0 ^ ^j ^ L - ¹ p 0 x 0 = f 0 ,

решение которого может быть вычислено рекуррентно по формулам:

x 0 = f ) / P 0

x j + 1 = Q j x j ¹ P j + 1 ⁺ j ¹ P j + 1 ,⁰ ^ ^j ^ L ^{— 1}

Будем считать, что формулы (13) реализуют устойчивые вычисления, то есть относительно q₅ I p_{j+ 15} 0 <  j <  L — 1 потребуем, чтобы абсолютные значения этих величин не превышали 1.

В соответствие с идеей параллельной прогонки Яненко разобьем интервал изменения индекса (0, L ) M точками на M + 1 подинтервал, и будем считать, что каждый подинтервал в свою очередь разбит на N + 1 интервалов. Значения искомой функции x k при k = N + 1 , 2( N + 1) , 3( N + 1) , … примем за параметрические неизвестные и обозначим через x [ k ] . Глобальный индекс j узла сетки свяжем с его локальным индексом i на k- подинтервале распараллеливания по формуле: j = i + ( k – 1) n.

При этом сеточную функцию g будем индексировать двумя способами: с помощью глобального индекса j и локального индекса i на к -подинтервале распараллеливания, тогда: g. = g_t [ k ] .

Целесообразность подобной индексации, в отличие от (2), определяется тем, что далее мы будем вынуждены ввести еще и индекс, соответствующий слою разностной схемы по времени.

На подинтервале [ k ( N + 1) , ( k + 1)( N + 1)] решим следующие вспомогательные задачи (предрешение задачи):

Pt + i [ k ] u ⁽⁰⁾ - '+ i [ k ] — Q i [ k ] u ⁽⁰⁾ i [ k ] = f ₊ i [ k ], i = 0,1...

P ₀[ k ] u ⁽⁰⁾ 0 [ k ] = 0,

Pi _{+ 1} [ k ] u ⁽¹⁾ i + i [ k ] — q i [ k ] u ⁽¹⁾ i [ k ] = 0, i = 0,1...

p ₀[ k ] u ⁽¹⁾ 0 [ k ] = 1.

Индекс k в квадратных скобках означает соответствующий подинтервал распараллеливания и изменяется от 1 до M + 1. Тогда в силу линейности задачи на каждом подинтервале:

[ k ( N + 1), ( k + 1)( N + 1)]

имеем представление, эквивалентное (4):

x i .[ k ] = u®[ k ] x _{k (} n _+n + u_ ⁽⁰⁾ [ k ], i = 0,1,...

Подставляя это выражение при i = k ( n + 1) – 1 в разностное уравнение, записанное для узла распараллеливания k , получаем разностное уравнение модуля обмена:

P km x km ^— Q km — i^n — i ^{[ k — 1]} x km — 1 = ^f Im ⁺ Q km — 1 ^^ ^{[ k — 1] k} = ¹ ,... m ,

решение которого, вместе с формулами (16) и предрешением задачи (14), (15), определяет искомое решение задачи (12).

Устойчивость вычислений по (17) устанавливается непосредственно. Нетрудно видеть, что:

i - 1

и(1)i[k] = П 9/[k]/Pui[k] и в силу устойчивости численного алгоритма для исходной задачи i=1

алгоритм реализации модуля обмена тоже устойчив. Указанный подход применим и к разностным уравнениям выше второго порядка с граничными условиями Коши.

Описание алгоритма распараллеливания вычислений по схеме бегущего счета

Для иллюстрации применения этого подхода для распараллеливания вычислений по схемам типа «бегущего счета» рассмотрим смешанную задачу Коши для простейшего гиперболического уравнения в предположении положительности коэффициента a:

ди ,    . 6 и                                            , .       „         ,. „        _

--+ a ( x , t ) — = f ( x , t ), и (0, t ) = g ( t ), и ( x ,0) = r ( x ) при 0 <  x <  Lh ,0 <  t <  T dt        '6x

Для решения смешанной задачи Коши применим неявную разностную схему:

m + 1 u j

—

т

m         m + 1

uu -j + a™^-

—

h

m + 1

u j- = Fm, и m = gm, и0 = r.

Реализация неявной разностной схемы приводит к двухточечному разностному уравнению m+1 u

m

К j  nm+1 +       Hm + T Fm

1 + K m  j ^{— 1}    1 + K m j 1 + K m j

При соответствующих начальных и краевых условиях. Иллюстрацию подхода проведем для случая разбиения [ 0, L ] на два подинтервала [ 0, L / 2] и [ L / 2, L ] , на которых выполним предрешение задачи в виде решения следующих двухточечных разностных уравнений сеточных задач при переходе с одного временного слоя m на следующий m + 1:

w ( ⁰⁾ [ k ] = -^Ki— w (^ k ] + — и ” + ^T F m , w ( ⁰⁾ = 0, i = 1,... L1 2

i        1 + K m  i ^{— 1}       1 + K m i 1 + K m  i ⁰

m w® [ k ] = —w—1[ k ], w01) [ k ] = 1, i = 1,... L12                (22)

1 + K m

Значение индекса k = 1, соответствует первому подинтервалу, k = 2 – второму, под индексом i следует понимать локальный индекс соответствующего подинтервала, связанный с глобальным номером j узла сетки по формуле:

j = i + L /2·( k – 1), k = 1,2.

В качестве параметрических неизвестных выберем значения искомой функции в узлах сетки j = L/ 2 и j = L в момент времени m + 1. Нетрудно видеть, что модуль обмена для определения параметрических неизвестных { ^ } , при j = 1 соответствующему узлу сетки L / 2 и j = 2 соответствующему узлу сетки L имеет вид:

« 1

m

K /2     (1) г     m +1

TTT j- w l /2 — 1 ^[1] g

^{1 + K} l /2

m

+ ^Kl^²^ w⁽⁰⁾l /2 — 1 [1] +

1 + K j/2

1 + K m 2

m , T и/ / ? + l/2   1 + к-т

^{1 + K}l /2

Fm, (24)

m

-^w ^—1 ^{[2] a} 1 ⁺

^{1 +} K j

m l    w(0) l/2—1[2] +

1 + K m

1 + K m

um

+ - ^T- F m .

1 + K m  l

Заметим, что при небольшом количестве точек распараллеливания модуль обмена может быть реализован аналитически, не прибегая к «услугам» компьютера. Эта особенность может представлять определенный интерес в случае реализации алгоритма распараллеливания на многоядерных процессорах с небольшим количеством ядер.

Следующее замечание касается другого крайнего случая – когда точек распараллеливания достаточно много, а узлов, в которых осуществляется предрешение задачи мало. Тогда параллельная прогонка Яненко может выступать как эффективный способ редукции неизвестных. Эта возможность обсуждалась нами в [6].

Применим этот подход для распараллеливания вычислений по неявной схеме Л.Д.Ландау, Н.Н. Меймана, И.М.Халатникова как иллюстрации распараллеливания вычислений по схемам типа «бегущего счета». Описание схемы и алгоритма расчета приводится по [7]. Для уравнений изоэнтропического течения:

поставим смешанную задачу Коши:

d s d t

—

9 s a — = ^F 1 , 9 x

d r    d r „

--+ a — = F dt    dx

д r

u = r + s = f ⁽ t ), q = ⁰, r ^— s = g ⁽ t ), q = q о ^{r (} q ^,0) = r o ⁽ q ), s ⁽ q ^,0) = s о ,⁰ ^ q ^ q о -

Простейшая неявная схема решения задачи имеет вид:

m + ¹ _ m s j s j

T m+1 _ m rj      rj

T

-

_am _j

+ a

m

F j

m ^{+ 1 s}j + 1

m ^{+ 1}

rj

-

h

s m ^{+ 1}

jm

F 1 j

m + ¹ r i — 1

h

m

F 2 j

r m + s m = 2 f m

m rN+1

—

mm sN+1 g

r j = г j , ^s°j = s о j ^,( N + ¹⁾ h = q о

Формулы позволяют устойчиво считать r слева направо, пробегая последовательно индексы j = 1, 2, N + 1. Аналогично устойчивые вычисления s реализуются справа налево в порядке убывания индекса j. В [7] дается следующее описание реализации алгоритма расчета. Краевые условия рассчи- тываются следующим образом. Величина

m + 1

s о   сначала определяется по формуле явного счета:

m + ¹

s ₀

= (i — _K m ) s m + K m s m + f о т

после чего r m ^{+ 1} определяется с помощью (30). Из соотношений (29) рекуррентно - слева направо - определяются r m ^{+ 1} . Из условия (30) определяется s N + 1 , после чего из соотношений (29) рекуррентно - справа налево - определяются s m ^{+ 1} . Пришедшее в левую границу значение s m ^{+ 1} не совпадает со значением, полученным из (30); поэтому необходимо уточнить значение s m ^{+ 1} . Так как формулы (29) определяют r m + ¹ как линейную функцию от r m ^{+ 1} , а s m ^{+ 1} - как линейную функцию от s_N ^{m +} ₊ ¹ ₁ , то достаточно сделать один пересчет с последующей линейной интерполяцией.

Предположим, что узлы сетки, введенной на отрезке (0, q0) изменения пространственной переменной для s и r структурированы в соответствии с идеей распараллеливания по Яненко, то есть они разбиты точками распараллеливания на m + 1 подинтервал, а каждый подинтервал в свою очередь разбит на n + 1 узлов. Примем обозначения N = (n + 1) · (m + 1), q0 = h · (N + 1). Переход со слоя по времени с номером m осуществляется по известным значениям rm и sm путем расчета значений sm+1, rm+1 по двухточечным разностным уравнениям:

К sm+i =       s™ь; + -^(rF™ + sm). j = N. N -1,...0,(32)

j              m j+1           m     1 jj

1 + Кj        1 + Кj

К1

rm+1 = KVS + vF^ rm). j = 1-2-N+1.(33)

1 + K m      1 + K m

Продемонстрируем предрешение задачи для конкретизации перехода с временного слоя m на слой m + 1. Пусть s⁽⁰⁾, s⁽¹⁾, r⁽⁰⁾, r⁽¹⁾ решения следующих задач:

s ⁽⁰⁾ : s N = 0.

K m

—s m + +----- ( T F m + s m ). j = N . N - 1....0.

1 + Km j+1   1 + Km    1 j j k™

,(1) . „  _ 1 c™+1 _ j   „™+1

^{s : S} n 1- ^sj               ^sj + 1 . j N . N   ¹-...⁰

1 + K m

r ⁽⁰⁾ : r ^(O) o = 0. r m ^{+ 1} =   "    r ™ +¹ + —^( r F™ + r m ). j = 1-2-... N + 1.

- j      1 + Km j-1    1 + Km    2 j j         - --

K m

r(1) : r(1)0 = 0.rm+1 = —r™+1 + -^(rF™ + rm). j = 1.2....N +1. - j      1 + k™ j-1    1 + k™    2j j. .

Определение этих искомых функций с конкретными граничными условиями на m + 1 слое будем называть предрешением задачи. В силу линейности задачи определения искомых функций на m + 1 слое по времени имеет место представление:

s"¹ = s + s N" ^{+ 1)} s «. j = N ...0.

r ™ ^{+ 1} = r ⁽⁰⁾ + r _D ⁽ ™ ^{+ 1)} rj ⁽¹⁾ . j = 0.... N + 1.

С помощью которого можно конкретизировать расчет по неявной схеме Л.Д.Ландау, Н.Н.Меймана, И.М.Халатникова по части вычисления граничных условий на m + 1 слое по времени. Действительно, подставляя представление решения через предрешение задачи в граничные условия:

™ +¹      ™ +¹

' 0   ⁺ s 0

2 f ™ ^{+ 1}

™ ^{+ 1}

' N + 1

„ ™ + 1      -^rn + 1

^S N + 1 = g

получаем:

™ +¹

^sN + 1

_r(⁰) __r(⁰)/⁰)₊ 2f ™ ^{+ 1}

' N +1    ' N +1 s 0   ^{+ 2} f

' N + 1

_ ™ + 1 ^g

^r 0

™ + 1

(1)  (1)

^{1 +} s 0 ' N + 1

_{7 f} ™ + 1 ™ + 1 (1) _ (0) _ „(1)„(0) ² J ⁺ g s 0 s 0 s 0 ' N + 1

Гн?1/1

1 + s ₀ r_{N + 1}

Далее реализацию граничных условий будем осуществлять именно таким образом с помощью предрешения задачи и на вопросе вычисления граничных условий останавливаться больше не будем.

На каждом подинтервале распараллеливания «предрешим» задачу на m + 1 слое в виде:

s ⁽⁰⁾ : s ⁽⁰⁾ N [ k ] = 0. s (⁰⁾ ™ ^{+ 1} [ k ] =   ^KTVk_T ]  s <01) ™ ^{+ 1} [ k ] +      ^    (TF1 ™ [ k ] + s ™ [ k ]). i = N . N - 1,...0,

1 + K ™ [ k ]            1 + K i [ k ]

m

5 ⁽¹⁾ : 5 ⁽¹⁾ N [ к ] = 1, s i ¹ m ^{+ 1} [ к ] = —^ 5 ^⁺¹ [ k ], i = N , N - 1,...0, 1 + K m

r(0) : r(0)0[к] = 0,r(0)m+1 [к] = K [k]  r' 0'm+1 [к] +-----1-----(Fm[к] + rm[к]),i = 1,2,..N +1, i            1 + Km [ к ] i1 + Km [ к ]    2 i       i

r ⁽¹⁾ : r ⁽¹⁾0 [ к ] = 1, r i ⁽¹⁾ m ^{+ 1} [ к ] =

K m [ к ] 1 + k ™ [ к ]

r i w m ^{+ 1} [ к ] +

,   \_T1A F m [ к ] + r m [ к ]), i = 1,2,.. N + 1.

1 + K m [ к ]

Знание величин:

v⁽⁰⁾П1 v⁽¹⁾ni ⁽⁰⁾ГЛ/+ 11 s^rM + ll и г⁽⁰⁾П1 г⁽¹⁾П1 г⁽⁰⁾ГЛ/ + П г ⁽¹⁾ГЛ/ + 11

⁵ 0 Ш, ⁵ 0 ^[1] , ⁵ n ^[ M ^+1], ⁵ n L M ^{+ 1]} и r 0  ^[1 J, ' 0 ^[1] , r N ^[ M ^{+ 1]} r N ^[ M ^{+ ±]}

т + 1 „т + 1 mm + 1   m + + 1

совместно с краевыми условиями позволяет найти значения 5₀   , s_L  , r₀   , r_L   по (40),(41).

Пусть {a k }, {fi k } - значения искомых функций s, r в узлах распараллеливания, тогда нетрудно видеть, что для них в узлах распараллеливания имеют место двухточечные разностные уравнения, которые в соответствии с принятой терминологией формируют модуль обмена:

m+i _  К0 [к] „Юга-m+m+1 ।     1     m-mXL-Ъ(0)ГИ -i- тРт      nml+ll ак   = ,    mrnS0 [к]ак+1 + ,    mr7i(K0[к]50 [к] + TF1,0[к] + a0 [к]),

1 + K m [ к ]             1 + K m [ к ]

m вт+1 =   0 [к] r(1) [к -1]em+1 +----1----(Km [к]r<0) [к -1] + TFm [к] + em [к]).(43)

к X^K^Vk ]              1 + <ВД

Параллельный (одновременный) расчет теперь организовывается аналогичным способом, что и для параллельной прогонки Н.Н.Яненко.

Нетрудно видеть, что четно-нечетная редукция и редукция произвольного числа неизвестных организовывается и в этом случае очевидным образом.

Несколько иной способ распараллеливания, чем тот, который реализован в параллельной прогонке Яненко, может быть использован для решения СЛАУ с нижней (верхней) треугольной матрицей. В качестве исходной рассмотрим задачу определения решения СЛАУ с нижней треугольной матрицей:

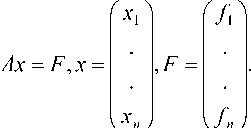
В силу линейности ( n + 1) искомое решение может быть представлено в виде:

x = f _ x ^(1,0,-⁰⁾ + f , x ^(0,1,-⁰⁾ + ... + f n x ^(0,-^0,1) ,                                (45)

(1,0,...0) (0,1,...0) (0,...0,1)

где x , , , x ,, ,..., x , - вспомогательного решения ( n + 1) при правых частях специального вида – все компоненты этих правых частей равны нулю, за исключением одной, равной 1. Предрешением исходной задачи ( n + 1) будем называть вычисление такого множества вспомогательного решений x ^(1,0,-⁰⁾, x ^(0,1,'"⁰⁾,..., x ^(0,-^0,1) . Нетрудно видеть, что первые к - 1 компонент соответствующего вспомогательного решения равны нулю. Например, только компонента под номером n вспомогательного решения x ⁽⁰’-^0,1) равна a - 1 , где а_у - коэффициенты матрицы A.

Эти группы искомых неизвестных и компонент правой части обозначим как x ⁽¹⁾, x ⁽²⁾,..., x ⁽ л ) и f ⁽¹⁾ , f ⁽²⁾ ,..., f ⁽ л ) . Для простоты изложения ограничимся одинаковым числом неизвестных в каждой группе, хотя выбор числа неизвестных в группах представляет важную задачу с точки зрения балансировки загрузки процессоров. Исходная СЛАУ может быть переформулирована в терминах x ⁽¹⁾, x ⁽²⁾,..., x ⁽ л ) и f ⁽¹⁾ , f ⁽²⁾,..., f ⁽ л ) как:

A n x ⁽¹⁾ = f ⁽¹⁾ ,

Д _х(2) _ Я²) _ д (1) 22 ^x = f     ^21 ^x ’

Д _х(3) _ Я³) _ д (1) _ д (2) ./1зз x   — f      -^/131 x     ^32 x   ,

Д _x ( l ) _ f ( l ) _ д           _ д   _y( l -1)

A ll x   ^— J      A l 1 ^x     .... ^All - 1 ^x    .

Матрицы A определяются соответствующими строками и столбцами исходной матрицы коэффициентов СЛАУ соответствующими разбиением искомых неизвестных и правой части на группы x ⁽¹⁾, x ⁽²⁾,..., x ⁽ л ) и f ⁽¹⁾ , f ⁽²⁾,..., f ⁽ л ) . Выполним предрешение задачи ( n + 3) понимая под правой частью к – задачи величину:

k - 1

Ф к = f ⁽ k ) - 2 A ki x ( i ) .                                       (47)

i — 1

Предрешение задачи допускает параллельные (одновременные) вычисления. Далее вычисляем значения искомых неизвестных, входящих в первую группу { x ,... x _m} , так как значение компонент, входящих в первую группу правых частей нам известны. После определения значений искомых неизвестных входящих в первую группу мы в состоянии вычислить величину Ф₂, с помощью которой мы вычисляем вторую группу искомых неизвестных и т.д. Таким образом, предлагаемый параллельный алгоритм решения исходной задачи состоит из этапа предрешения задач, которые могут реализовываться параллельно, соответствующего вычисления правых частей Ф, и последовательного вычисления искомых неизвестных по группам. Следует отметить и возможность использования параллельных вычислений для определения Ф_Л .

Если параллельная прогонка Яненко организовывается путем декомпозиции исходного алгоритма по краевым условиям, то приведенный выше алгоритм организовывается путем декомпозиции вычислений по правым частям и, на наш взгляд, его естественно назвать «распараллеливанием по правой части» в отличие от «распараллеливания по краевым условиям», реализованным в параллельной прогонке Яненко.

Заключение

Организация параллельных вычислений приводит, во-первых, к необходимости их широкого освоения, во-вторых к пересмотру ряда базовых понятий вычислительной математики – например понятия экономичности вычислительного алгоритма. В статье подход, называемый как «прогонка Яненко» в среде отечественных вычислителей-прикладных математиков, распространяется и на схемы типа «бегущего счета». Предлагается ввести понятия «распараллеливание по правой части» и «распараллеливание по краевым условиям».