Об особенностях применения метода быстрых разложений при решении уравнений Навье-Стокса

Математическая модель вязкой жидкости Навье–Стокса является нелинейной и поэтому одной из сложных. Получить решение подобных уравнений в аналитическом виде удается только в некоторых частных случаях. В данной работе такое решение получено при помощи нового метода – метода быстрых разложений.

Материалы и методы исследований

• 1.    Метод быстрых разложений . Математическое обоснование метода изложено в [1]. Его необходимо дополнить следующими положениями.

Пусть f ( x ) e C ^{( 2} ) ( 0 <  x <  a ) . Представим f ( x ) равенством

Nx f ( x) = Ch2 ( f ( x )) = M2 ( x ) + ^ fm sin mx -, m =1

I x 1, x

M 2 = A i I 1 — I + A —+ A 3

a J a

„ I x ³

⁺ A 4 I

I 6 a

—

..2     ..3...A x    xax

----    + (1)

2   6 a    3 J ^{v 7}

ax 1

6 J ,

где N – число учитываемых членов в ряде Фурье. Величины A1 ч A4, fm - коэффициенты быстрого разложения, вычисляемые по правилу:

A = f ( 0 ) , A 2 = f ( a ) , A 3 = f "( 0 ) , A 4 = f "( a ) , ₂ a                         _x         (2)

f m = — J( f ( x ) — M ₂ ( x ) ) sin mn—dx .

Правая часть в (1) для f ( x ) называется оператором быстрых синус-разложений второго порядка Ch ₂ , состоящим из операций, указанных в (2). Оператор быстрых косинус-разложений третьего порядка Ch ₃ при выполнении условия f ( x ) e C ^{( 3 )} ( 0 <  x <  a ) определяется выражениями:

^f ( x ) = Ch ( ^f ( x ) ) = M 3 ( x ) + ^f , +

N

+ Z f m m = 1

x cos mn —,

a

M ₃ = B 1 1 x

^^^^^^B

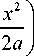
+ B₂x - +

2 2 a

I x     x ax 1 I xax

+B.     --- + B —

³ ( 6 24 a 6 J    ⁴ ( 24 a 12 J

Коэффициенты    косинус-разложения

B 1 ч B ₄, f , , f _m вычисляются по формулам:

B = f ‘ ( 0 ) , B 2 = f ‘ ( a ) , B 3 = f "( 0 ) ,

B 4 = f "( a ) , f , = ¹ f ( f ( x ) — M 3 ( x ) ) dx ,    (4)

a ₀

f_m = 2 f ( f ( x ) — M ₃ ( x ) ) cos m n -dx . a 0                          a

Метод допускает использование операторов

Chp с различными порядками p > 0, что зависит от порядка рассматриваемой дифференциальной системы. Операторы Ch0 и Ch1 нулевого и первого порядков также будут использоваться в данной работе. Они имеют вид:

Nx f (x) = Ch0 (f (x)) = M0 (x) + Z fmsin m^ , m=1

M 0

= A

1 —

x

a

+ A 2 a , A = f ( 0 ) , A 2 = f ( a ) , ⁽⁵⁾

2ax fm =-J(f (x) — M0 (x))sinmn-dx. a0

^f ( x ) = ^Ch 1 ( ^f ( x ) ) = ^M 1 ( x ) ^{+ f} ) ⁺

N x

+ E fm cos m^ ”, m=1

_ I    x11

M. = B x — + B,— , B. = f'(0), 1      11      2 a J     2 2a

1 ^a

^B 2 = ^f ' ( ^a ) , ^f > =-J ( ^f ( x )^{— M} 1 ( x ) ) dx , a ₀

f_m = 2 °a ( f ( x ) — M 1 ( x ) ) cos m n -dx . a ₀ a

Функции M_p ( x ) , p = 0,1,2.... называются граничными, так как определяются значениями f ( x ) и ее производными на границах отрезка [ 0, a ] . Граничные функции имеют специальную конструкцию, которая и обеспечивает быструю сходимость используемых рядов Фурье. В работе [1] доказано, что в быстрых разложениях ряды Фурье по синусам и косинусам быстро сходятся во всей области, включая границу, вследствие чего число учитываемых членов N весьма незначительное и объем вычислительной работы на ЭВМ при построении решения будет небольшим. Кроме того, полученное приближенное решение будет справедливо не только внутри области Q , но и на ее границе, что является существенным положительным качеством.

Если f ( x ) неизвестная функция, то задача сводится к нахождению неизвестных коэффициентов A 1 ч A 4 , f m или B 1 ч B 4 , f , , f_m , m = 1 ч N из некоторой алгебраической системы небольшого объема. При использовании быстрых разложений для решения дифференциальных систем надо учитывать следующие свойства оператора Ch_p :

dCh2 f dxx = Ch1f , d2Ch2 f /dx2 = Ch0 f, dCh3 f /dx = Ch2 f , d2 Ch3 f /dx2 = Ch1f , d3 Ch3 f /dx3 = Ch0 f.

То есть, порядок производной понижает порядок p оператора Chp на такую же величину, интегрирование повышает этот порядок. Данное свойство оператора Chp надо учитывать при подстановке быстрого разложения в дифференциальное уравнение. Отсюда вытекают следующие два правила, используемые при рассмотрении некоторой дифференциальной задачи.

Правило 1. Если f ( x ) представлена быстрым разложением оператором Ch m f ( x ) порядка m , то после подстановки данного разложения в дифференциальное уравнение n -го порядка к полученному уравнению после указанной подстановки следует применять оператор Ch m - n порядка ( m - n ) > 0 .

Правило 2. Пусть в дифференциальном уравнении некоторые два члена с неизвестными функциями представлены быстрыми разложениями порядков m ₁ и m ₂ и от них в данном дифференциальном уравнении вычисляются производные порядков n ₁, n ₂ соответственно и пусть 0 <  m 1 - n 1 <  m 2 - n 2 . Тогда для нахождения неизвестных функций к данному дифференциальному уравнению следует применить оператор Ch m - n , соответственный меньшей разности порядков m 1 - п 1 . Если в дифференциальном уравнении присутствуют более двух членов с неизвестными функциями в форме быстрых разложений, то поступают аналогично, определяя наименьшую разность порядков 0 <  m j - n j .

2. Постановка задачи . Границу области Q криволинейной трубы зададим неравенствами:

Q = { 0 <  x <  a , У 1 ( x ) <  y <  y 2 ( x ) } , y 1 ( x ) = b ( 1 - cos 2 n₀ n x]a ) ,           (7)

y ₂ ( x ) = h + b ( 1 - cos 2 n ₀ n x/a ) .

Граничные условия (8) и (9) согласованы между собой в углах области Q , что является важным обстоятельством при построении гладкого решения без разрывов. Для давления зададим условие только в одной точке из Q , например, в левом нижнем углу плоской трубы

P ( 0,0 ) = P             (10)

Запишем уравнения движени несжимаемой жидкости Навье-Стокса:

_ТТ д U _ ЭU 1 д P д ² U д ² U U + V + —-— = —_г +—_г , д x     д y   pv ² д x   д x ²    д у ²

д V    д V   1 д P  д ² V  д ² V

U — + V — + —2- — = —2- + —2-.

д x     д у   pv ² д у   д x ²    д у ²

Перекрестным дифференцированием из (11) исключим давление P :

д(_ггд U „ дU I д <_гд V „ V V

—I U --+ V --I--I U — + V— д у ( д x     д у J д x ( д x     д у

= д р ² U д ² U | др ² V д ² V ^Л д у ( д x ²    д у ² J д x ( д x ²    д у ² _?

К уравнению (12) добавим уравнение

несжимаемости

д Ufixx + д V ^ 3У = 0.            (13)

Параметры h , a , b , n ₀ считаем заданными, n ₀ - целое число. Параметры и уравнения нижней и верхней границ y ₁, y ₂ могут быть заданы и другими гладкими функциями, все последующие рассмотрения при этом останутся справедливыми. Слева и справа труба ограничена плоскостями x = 0, x = a . Проекции скорости частиц вязкой жидкости обозначим через ( v U, v V ) . Сомножитель v - кинематическая вязкость здесь добавлен для удобства дальнейших вычислений.

Граничные условия запишем в виде прилипания жидкости на верхней и нижней стенках плоской трубы

Получили систему двух уравнений (12), (13) с двумя неизвестными U , V .

Математически задачу поставим так: в классе непрерывных и гладких функций ( U , V ) е C ^{( 3 )} ( Q ) найти решение системы дифференциальных уравнений (12), (13) с граничными условиями (8), (9). После нахождения U , V давление P определим из системы (11) с граничным условием (10).

3. Построение решения методом быстрых разложений. Анализируя уравнение (12), можно заметить, что здесь от U по переменной x берется старшая частная производная второго порядка, а от V третьего порядка. Поэтому компоненты скорости U , V представим быст-

рыми разложениями по переменной x на отрезке 0 <  x <  а в виде

N x

U = Ch ₂ U = M ₂ + ^ u_m ( y ) sin mn— , m = 1                  a

N

^V = ^Ch3^V = M 3 + ^u 0 ( У ) + £ U n ( У )

n = 1

x cos n n —.

a

। У = У 1 ( ^x )

= V = U|

У = У 1 ( ^x )

I о = V|

¹У = У 2 ( ^x )

= 0.

¹У = У 2 ( ^x )

На входе и выходе из трубы профили скоростей зададим по закону Пуазейля

^VL = 0 = V x = a = ⁰ , ^UV = 0 = U x = a = q 0 У ( ^h - У ) . ( ⁹ )

x I , , x , . [ x x

^^ 2 — A 1 1 1 — I + A 2 —+ A 31---

I    a J      a I 2   6 a

⁺ A 4

6 a

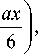
M ₃ = B 1 1 x -

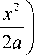
+ B₂x - +

²2 a

x

ax I -   +

3 J

x    x    ax I I x    ax

---- + B --

6   24 a    6 J    ⁴1 24 a 12

В дальнейшем будут использоваться сле-

дующие выражения для частных производных

от U , V , представленных разложениями (14), (15):

V = B _; l x

x 2	x 2	f x 3	x 4	ax 2
	1+ B 2 2 a + B 3 1
2 a		v "6	24 a	6

+

x

U = A i l 1

x

a

x

+ A 2--+ A 3

x ²

x ³

ax

^{+ B} 4

x ⁴

—

—

a

6 a

+

24 a

ax ² 1            N

77 1 + ^U o ⁽ y ) ⁺ Z u ⁽ y )

¹² J              n = 1

cos nn— ,

a

+ A ₄

x ³

ax

—

N

6 a

+ n

m = 1

u m

x

sin mn —

a

,

d y

d U = A 2 — A ,

d x	a
f x 2	a
+ A 4 1 T" V 2 a
	6

+ A 3 1 x

x ²

a

—

—

2 a

+

d V „ x ^ x X _ ( x2 x3 — = в, 11 — — + B^ — + B. dx      V 23 a J      a      1 T 6a ax ax

^{+ B} 4

x ³

+

N-^пл: . x N , —u_n sin nn — n = 1 a a

,

EN mn m=1 a

6 a

a

d V x2 x2 x3 x4 ----= B, l x — + B‘ — + B‘\ x 5y     V 2a J 2 2 a 31 6 24a ax2

a x4

+

u_m cos mn —,

+ a 4

d U = a ; i

x л	x	f x2_	x 3	ax 1
	1 + A 2--+ A 3 l			— +
a j	a	v 2	6 a	3 J
x 3 — 6 a	ax 1 — 1 T l+ N um 6 J m = 1	x sin mn — a		,

a

a x2

x ²

+ в‘

d² V

d x ²

24 a

B 2

a

d ² u _ A — a ;

d x d y

a

—

—

2 a

+ A 4

2 a

—

+

U = A f i d x ^{2      3} V

—

d ³ u

d x ² d y

= A l 1

E ⁿ mn ,

---um m = 1 a

x

cos mn —,

a

x

a

x

—

a

, x N f mn

^{+ A} 4— n\ — a m = 1 V a

m = 1

u m

x

sin mn —,

a

d2U=A' fi dy2     1V

—

x

a

+ A 4

x ³

6 a

„x N f mn ^{+ A} 4— n\ — a m -; V a

m = 1

+ A 2 ' x + A ₃"

ax

—

a

N

+ n

m = 1

^x um sin mn —,

a

x ²

x ³

ax

—

—

6 a

x

u m sin m n— ,

a

+

8^U   m

8 y¹ " A

x

a

+ A ” x + A₃^m

x ²

x ³

ax

—

—

+ A f

x ³

ax

—

a

6 a

+

N

6 a

+ n

m = 1

u _m

x

sin mn —.

a

(

a ; | i

x

a

x

+ A 2 —+ A 3

a

+ A 4

ax

N

(

+

(

+

x ²

x ³

ax

Л

6 a

6 a

m = 1

x u m sin mn —

a

A 1 |1

⁺ A

A 'il

+ A 4

v

x

x

x ²

x ³

ax

a

a

6 a

6 a

x

a

x ³

6 a

u _m sin mn —

+ A 2 x + A’

ax

x ²

x ³

a

ax

a

6 a

N

x

I N u' _m sin m n—

a

ax ² 1            N

77 1 ⁺ " 'f y ⁾⁺ N ^un ⁽ y )

¹² J              n = 1

x

cos nn— ,

a

N n ²n ²

a ²

n = 1

X V- = B ’l I

d x d y

+ B 4

d² V

d x d y ²

= B

+ в 4'

x ³

6 a

.a

x

a

B 1 --+ B-

| x —	x 2 2 a	a — 3,	J + B 41	x 2 v 2 a
2 П			x

a

U n cos nn— ,

a

+ в 2-+ в ‘

a

ax

x

a

x ³

6 a

V = B, fl d x ^{3     3}1

x ²

x ³

ax

6 a

+

N-^nn , . x N . — u_n sin nn- , n = 1 a             a

+ B 2 x + B 3

a

ax

—

—

x ²

x ³

ax

—

—

6 a

+

■N nn „ . x N, — U n sin nn- , n = 1 a              a

N 33 x I x n П - 1 + ^B 4 - + N — a J a    n = 1 a

n = 1

x

U sin nn— . n

a

Задача сводится к нахождению 9 + 2 N

неизвестных функций, зависящих только от одной

переменной y .

A ( y ) - ^A 4 ( y ) , B 1 ( y ) - ^B 4 ( y ) ,

u m ( у ) , ^U m ( у ) , ^U 0 ( у ) , m = ^{1 +} N .

Для нахождения

этих

неизвестных

подставим U , V из (14) в уравнения (12) и (13):

(

X

Л

л

+

X

(

A 2

a

A¹- + A

N nn + 4 = 1 т

A 2

a

x ²

2 a

x

u _n cos nn —

A 1

+ A 3 | x

a

⁺ A

x ²

2 a

a

Л

+

a

2 x

2 a

N nn , + 4 u ‘ cos n n — n = 1 a

b;\ x

+ B 4

x

a

a

+ A 4

2 x

2 a

a

+

x ²

2 a

x ⁴

24 a

+ в ‘ x -+ B 3

2 a

ax ²

x ³

x ⁴

ax ²

л

N

24 a

+

+

x u‘ cos nn—

a

j

A "

^^^^^^в

+

+ A 44

к

—

x

a

x ³

6 a

+ A 2 ' x + A "

a

ax

—

A — A

—--¹ + A

a

N m n +X— m = 1 a

A 1

—

—

—

N

+ X

x

—

u

x ²

2 a

+ A 4

B 1 I 1

—

x ²

—

x ³

6 a

ax

—

x

sin mn —

—

x

u m cos mn —

x

a

x

6 a

x

a

a

+

^B1 I x

—

x ²

2 a

x ²

2 a

x ³

—

x ⁴

24 a

ax ²

—

л

+

—

+ в 4

x ³

к

6 a

B 1 I x

—

—

^{+ B} 4

к

a

+ A ₄

x ²

2 a

a

—

a

x

+ A 2--+ A 3

—

ax

a

N

+ X

m = 1

u m

x ²

x ³

ax

к

—

—

6 a

x

sin mn—

a

+ B 4

x ⁴

ax ²

—

/

X

X

N

x

24 a

B 1 1

+ B 4

к

B 2

—

a

— X

n = 1

—

x

a

x ³

6 a

B

a ²

+ в 2 x + в 3

a

ax

—

—

и cos nn —

x ²

x ³

—

6 a

a

—

ax

к

+

—

—

+ B ₂ x + B 3

a

—

x ²

2 a

x ⁴

ax ²

—

x ²

x ³

ax

к

—

—

+

Ba x

x ²

—

2 a

24 a

NAnn   . x

X U _n sin n n — n = 1 a             a

x ²

2 a

a

—

x

u_n cos n n—

a

+ В 4

x ²

2 a

a

—

к

—

—

+ в 2—+ в "

2 a

x ³

x ⁴

ax ²

к

—

—

24 a

+

—

—

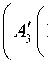
6a ax

—

N n n - X — °n n = 1 a	x sin nn — a
2	3	4
x	x 3	x 4
--+ Ba		—
2 a     3 1	6	24 a

— ax2

N

+ U + X

x ^N

^{+ A} 4    X

a

x

u n cos nn —

m n

m = 1

a ²

+ в 4

x ⁴

—

+

ax ²

a

x

u _m sin m n— 1 +

a

x

u _n sin n n —

a

24 a

b "I 1

+ в 4

A ,"I

+ A 4"

/

—

^^^^^^B

x

a

x ³

6 a

x

^^^^^^B

a

x

6 a

В Ц 1

^^^^^^B

x

a

+ B 4"

x ³

к

6 a

N

x

+ u0 + Xun cosnn— n=1              a

. ₀ x

x ²

x ³

ax

a

—

—

ax

—

—

6 a

к

+

Nnn . . x X--U" sin nn — n=1 a             a

+ A 2" x + A ""

—

a

ax

N

+ x

m = 1

x ²

—

x

—

6 a

x

u m sin m n —

+ в 2 x + в "

a

ax

—

—

ax

x ²

—

—

a

x ³

ax

к

—

6 a

+

NAnn „ . x X-- U n sin nn — n = 1 a             a

.

Зависимости U , V из (14) также подставим в уравнение (13):

A — a —---¹ + A 3

x

—

x ²

^^^^^^B

a

—

x ²

a

2 a

2 a

+ в 2—+

2 a

+ В 3

x ³

x ⁴

ax ²

—

—

24 a

+ в 4

x ⁴

—

ax ²

N

24 a

^{+ U} ■ X

x un cosnn- = 0.

n = 1

a

Теперь U , V из (14) подставим в граничные условия (9) и затем в (8):

A ( y ) = q о y ( h ^— y ) , A ( y ) = q о y ( h ^— y ) .

N

и ( y ) ⁺ X ^u m ( y ) = ⁰,

m = 1

aa 3     N

-( ^B 1 ⁽ y ^{) + B} 2 ⁽ y ) ) - —( ^B 3 ⁽ y ^{) + B} 4 ⁽ y ) ) ^{+ U} 0 ⁽ y ^{) +} £ ⁽ -0 ^U m ⁽ y ) = ⁰

^{2                    24}                              m = 1

u\   ,. = a ( y ) | 1 —- 1+ A ( y_v )- + a ( y_v ) | ———

^{1 y} = ^y > ^{( x} )      ^1V "k a 7      2^V a ^3V k 2    6 a

ax 1   , / J x

T | ^{+ A} 4 ⁽ У " ) I    ^—

3 7            k 6 a

ax 1

— I + 6 )

N x

+ Z Um ( У1 ) sin m^ = 0, m=1                  a

2     34

V|    .= B , ( y ) x — — + B ₂ ( y ) — + B ₃ ( y ) x—

^{1 y} = ^y > ^{( x} )     ^{1V 1} k 2 a 7     ^{2V U}2 a ^3V1 k 6 24 a

ax 1 „ / J x + B ₄ ( У )

6 7    ^{4V 1} k24 a

ax ² 1

--- +

12 7

N

^{+ u} 0 ( У 1 ) ⁺ E ^u n ( У 1 ) n = 1

x cos nn — = 0,

^U\_y = y ₂ ( x ) - ^A 1 ⁽ y 2 ) k ^{1 —} _a 7 ⁺ A 2 ⁽ y 2 ) a ⁺ A 3 ⁽ y 2 )

a

23 x ² x ³

—

26 a

ax 1    , , x Г x ³

T | ^{+ A} 4 ⁽ У 2 ) I    ^—

3 7            k 6 a

ax 1

— I +

6 7

N x

+ Z ^um ( y 2 ) sin mn- = 0, m = 1                   a

2     34

V|     . = B_v ( y ₂) x - — + B ₂ ( y ₂) — + B ₃ ( y ₂) x---—

^{1 y} = ^y 2 ^{( x} )      ^{1V 2}k 2 a 7     ^2V272 a ^3V 2k 6   24 a

ax 1 „ / J x ---- + B. ( y ₂) -----

6 )    ^{4V 2}k24 a

ax ² 1

--- +

12 7

N

^{+ U} 0 ⁽ y 2 ^{) +} Z

n = 1

x un (y2) cos nn — = 0.

Неизвестная U определяется через оператор Ch ₂ второго порядка, в уравнении (12) старшая производная по x тоже второго порядка, разность порядков 2 — 2 = 0 равна нулю. Составляющая V выражается через оператор Ch ₃ третьего порядка, в уравнении (12) старшая производная по x тоже третьего порядка, разность порядков 3 — 3 = 0 равна нулю. Из правил 1 и 2 следует, что к уравнению (17) надо применить оператор Ch ₀ нулевого порядка, который состоит из следующих операций:

1. Для нахождения первого коэффициента граничной функции оператора Ch ₀ следует положить в (17) x = 0:

2. Для нахождения второго коэффициента граничной функции оператора Ch ₀ положим в (17) x = a :

^{( A} 2 ^{— B} 2 )

Г A- z A ^a

k

Г A 2

+ A

aa

+— A o +— Ад + 6 ³ 3 ⁴

E z mn / mm

—^{( —} 1 ) u m m = 1 ^a

— A "

aa

+ — А " +- A 4 +

a 6 3 3

E N m n    m

—^(— 1 ) u m k m = 1 ^a

+

+ ( A "" B 2 )

+

if Г ^A 2    ^A 1

A 1 \

a

—

a . a . N mn 7 A 3 ^— T ^А 4 ⁺Z-- 3      6       m =1 a

u + m

2 ( B; + B " ) — 24 ( B 4+ B 4 ) +

N

^{+ u} "⁺ Z^{( —} 1У ^U "

k          n = 1

Л

+

Л Г A " + A1\

—

A

—

m n

a

a   a   N^m n

- A 3 ^— -A " -\--- U m

3      6       m = 1 a

+

+ ( A " — B " )

2 ( ^B 1 + ^B 2 ) — 24 ( ^B " + ^B 4 ) +

N

N

+ A " I ^u 0 + Z ^u n I⁺ A U ■ Z ^u k       n = 1     7 k       m = 1

—

„ Г A, — A,  a , a , N mn

—B1\  ---1 — т A" —7 A4 +Z---um k a      3      6 m=1 a

— (22)

U + £ ( — 1 ) ‘ U n k n = 1

Г B B + aB + aB a 6 3 3 4

—

—

—

— A Г B 22 B L — 0b₃ — aB — N 1     34

k a 3      6       n = 1

a ²

- Un

—

N 22

— Z n n ( — 1 ) n U n n = 1 a

= A 4 + A 2"— B 4 — B ".

— B 1 U"+ Z »"\ — B 1 U 0 + Z u ,

= A "+ A "— B ₃ — B "

3. Для нахождения коэффициентов Фурье оператора Ch ₀ умножим левую и правую части уравнения (17) на sin p n x/a при p = 1 + N и проинтегрируем по x e [ 0, a ] .

Эта операция весьма трудоемкая, так как связана с вычислением около двухсот определенных интегралов с особенностями при m = n, m + n = p, m - n = p, m - n = -p . Поэтому для нахождения коэффициентов Фурье для уравнения (17) заменим процедуру, которая заключается в умножении (17) на sin pn x^a и интегрировании, на поточечный метод нахождения этих коэффициентов [2]. Для этого отрезок [0, а] равномерно разбиваем на N +1 частей и получаем N внутренних точек с координатами x = xj = ja/(N +1), j = 1 + N. (24)

Крайние точки x = 0 , x = а не входят в число расчетных точек, так как они уже использованы при получении уравнений (21), (22). Теперь в левой части уравнения (17) последовательно положим x = x j из (23) и получим систему, которую формально запишем в виде

{ ( 17 ) , x = x , = j а/ ( N + 1 ) , j = 1 + N } . (25)

Можно доказать, что в пределе при N ^ ж коэффициенты Фурье, определенные интегральным и поточечным способами совпадают. Вычислительная трудоемкость при использовании поточечного метода существенно снижается, так как устраняется проблема вычисления сложных определенных интегралов. Полученная система (21) - (24) состоит из 2 + N уравнений

Перейдем к рассмотрению уравнения (18). В (13), следствием которого является (18), первое слагаемое У U / дx определяется оператором Ch 1 первого порядка, второе слагаемое д V / уу - оператором Ch ₃ третьего порядка. Из правил 1 и 2 следует, что к уравнению (18) надо применить оператор меньшего порядка из двух названных, т. е. Ch ₁ первого порядка, который состоит из следующих операций:

• 1.    Для нахождения первого и второго коэффициентов граничной функции оператора Ch ₁ следует продифференцировать (18) по переменной x и положить в нем x = 0 и затем x = а :

• 2.    Первое слагаемое в ряде Фурье перед тригонометрической суммой оператора Ch ₁ определяется интегралом по x е [ 0, а ]

• 3.    После подстановки разложений (14) в граничные условия (9) получим еще четыре уравнения

A 3 + B ’= 0 , A ₄ + B 2 = 0. (26)

A 2 ^- A 1 „ , ^² , D< ^{а 2      a 4}

--------а + в,--+ в-.--Bo-- a 13     26     345

- в ‘ — + и а = 0. 40

A = A = q0 у (h - у), U0 (у ) + £ и, (у ) = 0, n=1

вЛ + в₂^а - B^ - вД + и ( у ) +    (28)

• ¹ 2     ² 2     ³ 24     ⁴ 24     ⁰

• 4.    Для нахождения коэффициентов Фурье оператора Ch ₁ следует умножить левую и правую части уравнения (18) на cos p n x/а при p = 1 + N и проинтегрировать по x е [ 0, а ]

N

+ £ ^u n ⁽ у ^{)(- 1 ) n} = 0.

n = 1

(A4 (-1)p - A3 - B1+ B2 (-1)p ) + p п 4                  .         (29)

+^ “ p ⁺ p^a _П 4 ( B ‘- B 4 (^{- 1} ) ’ ) + 2 "'• = °-

Дифференциальная система (19), (20), (22), (23), (25)-(29) замкнутая, состоит из 9 + 2 N уравнений относительно такого же количества неизвестных, указанных в (16). Граничные условия для нее получим при помощи (21). К первому и третьему уравнению из (21) следует применить оператор второго порядка Ch ₂ , ко второму и четвертому – оператор третьего порядка Ch ₃ :

U ^ A (0) = 0, у=у1 (x), x=0

U ^ A (h) = 0, у=у2 (x), x=0

и ^ A (0) = 0, у=у, (x),x = а

U ^ A ( h ) = 0.

у=у2 (x), x=а1

Для нахождения решения задачи надо неизвестные коэффициенты A 1 - A ₄ , B 1 - B ₄ представить быстрыми разложениями.

Результаты исследований

Задача о течении вязкой жидкости сводится к решению замкнутой системы обыкновенных дифференциальных уравнений, которая может быть решена известными математическими программами. Получение решения в аналитическом виде представляет большой интерес, так как позволяет проводить анализ и исследовать влияние различных факторов на свойства течения вязкой жидкости в конкретных случаях.

Обсуждение результатов

Уравнения Навье–Стокса, описывающие движение вязкой жидкости, широко применяются для создания математических моделей при решении технических задач. Нахождение аналитического решения системы уравнений Навье–Стокса затруднительно из-за их нелинейности. Аналитические решения этих уравнений найдены лишь в некоторых частных случаях с простой геометрией или при существенных упрощениях. В других случаях применяется численное решение. В работе [3] получено аналитическое (в виде ряда Фурье) решение уравнения Навье–Стокса методом разделения переменных. В [4] приведен пример расчета ламинарного течения вязкой несжимаемой жидкости в канале постоянной ширины