Об особенностях работы некомпенсированной пьезокерамической антенны в скважине

Электронный журнал «Техническая акустика»

При разработке скважинных акустических антенн часто встаёт вопрос о поиске оптимальных соотношений между диаметром антенны и характерными размерами скважины. Знание этих оптимальных соотношений особенно важно при создании скважинных источников для интенсификации различного рода геотехнологических процессов акустическим полем из скважин. В этом случае принципиальным является введение акустической энергии в продуктивный коллектор с наименьшими потерями. В данной работе нас будут интересовать акустические пьезокерамические источники, находящиеся в скважине аксиально симметрично и излучающие упругие поля в массив через жидкий слой. Для таких источников условие максимального прохождения акустической энергии в массив означает, что система «антенна – слой жидкости – скважина» настроена в резонанс.

Рассматриваемая проблема близка к той, которая исследовалась в известном цикле работ, посвящённых расширению полосы пропускания цилиндрических пьезокерамических преобразователей с помощью различных переходных слоёв см., например, [1, 2] . Основные характеристики цилиндрических излучателей в этих работах рассматриваются с позиций точных уравнений теории упругости и законов пьезоэффекта, однако, в качестве акустической нагрузки предполагается жидкая среда.

Конкретная задача резонансного прохождения акустической энергии от цилиндрического скважинного источника в массив через жидкий слой рассматривалась, например, в [3–5]. Авторы работ [3, 4] моделировали подобный источник с помощью идеальных граничных условий, т. е. на поверхности источника задавались радиальные смещения. При этом был сделан достаточно очевидный вывод о том, что в данном случае условие резонансного прохождения близко к условию полуволнового резонанса коаксиального жидкого слоя, заключённого между двумя абсолютно жёсткими цилиндрическими границами. В [5] моделировался уже конкретный тип источника, а именно, кольцевой пьезокерамический. Авторы [5] пришли к заключению, что такой источник также можно моделировать идеальными граничными условиями и является он источником давления. Таким образом, условия резонансного прохождения в [5] совпали с условиями четверть волнового резонанса коаксиального жидкого слоя, заключённого между абсолютно мягкой и абсолютно жёсткой границами. В работе [6] исследовалась частотная зависимость сопротивления излучения цилиндрического пьезокерамического источника, работающего в скважине. К сожалению, авторами [6] не была рассмотрена на должном уровне задача о поиске оптимальных соотношений между характерными параметрами пьезокерамического излучателя и скважины для максимальной передачи акустической энергии из скважины в массив. Кроме того, результаты работы [6] трудно применить для исследования дифракционной структуры упругих полей в массиве, которые создаются протяжённой пьезокерамической антенной, находящейся в скважине.

Необходимо также отметить работу [ 7] , где ситуация, связанная с излучением пьезокерамического цилиндра в твёрдое полупространство из скважины моделируется с помощью метода конечных элементов. К сожалению, авторам работы [ 7] не удалось получить удовлетворительных результатов для всей исследуемой ими полосы частот излучения цилиндра. Значительные расхождения между теоретическими и экспериментальными данными наблюдались для частот, которые близки к частотам объёмных резонансов в системе «цилиндрический источник – жидкость – скважина».

Опыт изготовления и эксплуатации скважинных пьезокерамических некомпенсированных антенн [ 8] показывает, что частоты резонансного прохождения акустической энергии в массив, при использовании таких источников, существенным образом отличаются от теоретических, полученных с помощью идеальных граничных условий. Связано это с тем, что при расчёте режимов излучения пьезокерамической антенны в скважине необходимо учесть характер собственного импеданса такой антенны. Это возможно, например, если идеальные граничные условия при расчётах заменить на импедансные.

В данной работе пьезокерамическая антенна, излучающая из скважины в массив через жидкий кольцевой слой, моделируется с помощью известного метода эквивалентных электромеханических схем. Этот метод даёт возможность получить приближённые, но достаточно эффективные, импедансные граничные условия, и в дальнейшем сформулировать дифракционную задачу об излучении из скважины упругих волн в массив с помощью протяжённой пьезокерамической антенны. В работе получены также соотношения между характерными параметрами пьезокерамической антенны и скважины оптимальные для максимального прохождения акустической энергии в массив через жидкий слой.

ПОСТАНОВКА ЗАДАЧИ

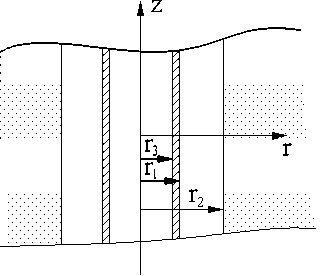
Рис.1

Рассмотрим следующую модель. Пусть в безграничной изотропной однородной упругой среде находится бесконечная круговая цилиндрическая полость радиусом r ₂ , которая заполнена идеальной сжимаемой жидкостью. Твёрдая среда характеризуется плотностью p s , продольной скоростью звука c_l , поперечной скоростью звука c t , упругими модулями к и ц , для которых выполняются известные соотношения: ц = p s c t 2 , к + 2 ц = p s c l2 ; жидкость характеризуется своей плотностью p f и скоростью звука c _f. В полости осесимметрично находится протяжённая пьезокерамическая антенна с внешним радиусом r ₁ и внутренним радиусом r ₃ , геометрия коаксиальной системы «антенна – жидкий слой – массив» представлена на рис. 1. Пьезокерамика, из которой состоит антенна, характеризуется плотностью p _c , скоростью распространения продольных волн в стержне c ₁ ^E , пьезоэлектрическим модулем d ₃₁ и модулем гибкости s ₁ ^E ₁ . Считаем, что пьезокерамическая антенна совершает осесимметричные колебания, поляризацию пьезокерамики предполагаем радиальной. Антенна возбуждается переменным электрическим напряжением U = U 0 e‘^Mf ( z ), где f ( z ) - нормированное распределение электрического напряжения вдоль образующей протяжённой цилиндрической антенны.

О ГРАНИЧНЫХ УСЛОВИЯХ

Для расчёта движения пьезокерамических преобразователей часто используется метод эквивалентных электромеханических схем (см., например, [9, 10]), который позволяет выразить в явном виде скорость движения границы преобразователя и корректно записать после этого граничные условия дифракционной задачи. Общая структура подобных эквивалентных схем известна и изображена на рис. 2, где Zel — импеданс электрической стороны преобразователя, Zm — механический импеданс преобразователя, Zl — импеданс нагрузки, N — коэффициент электромеханической трансформации, с помощью которого можно пересчитывать на электрическую сторону импеданс механической стороны преобразователя: Z^l = (1 / N 2)( Zm + Zl) и выразить внутренний импеданс преобразователя следующим образом: (1 / ze )=(1 / z„ )+(1 / zmm).

l.-lf Z.

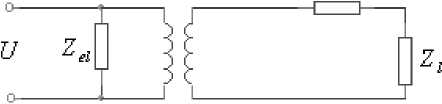
Рис.2

Для некоторых случаев колебаний радиально поляризованного бесконечно длинного цилиндра известны точные эквивалентные электромеханические схемы [ 11] , которые весьма сложны и неудобны для использования на практике, но на их основе можно получить достаточно простые приближённые эквивалентные схемы, например, при условии малой волновой толщины стенки цилиндра [ 9–11] , что выполняется практически всегда.

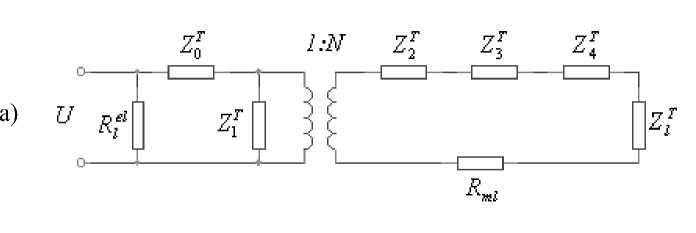
б)

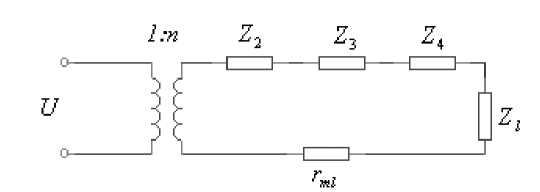
Рис 3.

Приближённая эквивалентная схема удобная для наших исследований представлена на рис. 3. На рис. 3а изображена эквивалентная схема протяжённой, но конечных размеров, пьезокерамической антенны, которая согласована с питающим генератором; введены следующие обозначения: ZT = imL, где L — внешняя индуктивность, компенсирующая статическую ёмкость антенны Ca, Z1 = 1 / (imCT), Ree — сопротивление электрических потерь антенны, которое можно выразить через тангенс диэлектрических потерь tgS : Re ~ 1 /(coCTtgd); ZT, Z3, ZT, ZT — интегральные эквивалентные импедансы, Rml — интегральное сопротивление механических потерь в антенне. На практике, чаще всего, удаётся введением внешней индуктивности согласовать антенну с генератором, причём, если у антенны невысокая добротность, согласование можно провести в достаточно широкой полосе частот [8]. Для дальнейшего анализа предположим, что достигнута идеальная компенсация статической ёмкости антенны, кроме того, пренебрежём величиной Rlel , так как обычно tgS для пьезокерамических материалов мал. Эти допущения приводят к эквивалентной схеме изображённой на рис. 3б. Здесь все величины импедансов, находящихся на механической стороне, нормированы на единицу длины антенны: Z2 = in2/(mCa), Z3 = i2nm8rapc, Z4 = 2п8/(iarasE\ n = 2nd31 /s 1E, rml — погонное сопротивление механических потерь, импеданс Z2 учитывает прямой пьезоэффект, Ca — погонная

ёмкость,  ra и  8 — соответственно средний радиус и толщина стенки пьезокерамического цилиндра. Используя определение коэффициента электромеханической трансформации n (см., например, [10]), получим, что величину колебательной скорости поверхности цилиндра можно выразить следующим образом:

V =_ nU_

Zl + Zm ’ где Zm = Z2 + Z3 + Z4 + rml, направление вектора скорости совпадает с направлением нормали к поверхности цилиндра, положительное направление нормали совпадает с осью r на рис. 1.

Перед дальнейшим анализом необходимо сделать следующее замечание. Эквивалентная схема изображённая на рис. 3б пригодна для описания не только протяжённого тонкостенного пьезокерамического цилиндра, работающего в районе первого радиального резонанса, но и антенны, состоящей из тонкостенных цилиндрических колец, при условиях: h <<2 r a , 8 <<2r a , A h <<2r a , где h — высота кольца, A h — расстояние между кольцами и при условии, что взаимодействие между кольцами мало [ 9, 10] .

Введём потенциал смещения в жидкости ф, при этом Pf =-Pf(д2ф/дt2), Vf = (д/д t )Уф , где Pf и Vf — соответственно давление и скорость в жидкой среде на границе пьезокерамического цилиндра, зависимость от времени определяется i о/ множителем e . Если пьезокерамический излучатель нагружен при r = r1 на удельный импеданс Zl, а при r = r3 поверхность является свободной (влиянием воздуха, который находится внутри антенны пренебрегаем), получаем следующие модельные граничные условия (см., например [11]):

° rr\r = r ₃ = ⁰, ° rr\r = r , =— ^{i O Z}U r ,                                                                      (2)

где u_r — радиальное смещение границы преобразователя.

Далее воспользуемся условием неразрывности нормальной составляющей колебательной скорости на поверхности цилиндра и получим вместо (1) следующее соотношение, выполняющееся на границе r 1 :

Уф +

РОф = ^U 0 f ⁽ z ^{) n} iZ m      i O Z m

Выражение (3) является тем необходимым граничным условием, с помощью которого можно сформулировать интересующую нас дифракционную задачу о распространении упругих волн в массиве при возбуждении их протяжённой пьезокерамической антенной, находящейся в скважине.

УСЛОВИЯ РЕЗОНАНСНОГО ПРОХОЖДЕНИЯ

Уравнения движения через потенциал смещения в жидкости у , продольный y l и поперечный у потенциалы смещений в массиве запишутся в виде:

д ² у 1 ду д ²у

+      ■ ,/■ k 2 у = 0;

д r   r д r д z д 2у1 1 ду1 д 2у

• —+ —— + —+ k 2 y l = 0;

д r²   r д r     д z²

• ^{д 2} у ^{1 д}у у ^{д 2} у 2   ₀

• ⁺— Б 2 ^{+    +} k t ^у = 0,

• д r    r д r   r     д z

где k _f , k_l , k_t — соответственно модули волновых векторов в воде, продольный в массиве, поперечный в массиве. Напряжения o _rr , о _rz и смещения u_r и u_z в массиве связаны с потенциалами посредством равенств:

о rr

л

= - а а у + 2 ц c_l

° rz

= Ц 2 ^{3 У}

д z д r

_ 2

u = ^д У 1 _ду . ^r д r дz ’

д У д r ² s I

^^^^в

2 ц ^У ; д z д r

^^^^^^^^

P s ^ у ;

u_z    '^у₊Ъу + у.

д z    д r   r

На границе r ₁ выполняется граничное условие (3), предположим также, что на границе r ₂ выполняются классические граничные условия, характерные для контакта жидкости с твёрдым телом, т. е. условия неразрывности нормальных составляющих смещений и напряжений и равенства нулю касательных напряжений:

• ^U r\r₂ = д r |^Г 2 ; ^О rr | r 2 = P Z | r 2 ’ ° rz | r 2 = ⁰ ’                                                                    ⁽⁶⁾

Процедура решения дифракционной задачи, сформулированной в выражениях (3)– (6), стандартна (см., например, [ 12] ). В дальнейшем нас будет интересовать поле объёмных деформаций S_V в массиве. Поле сдвиговых деформаций в массиве при возбуждении упругих волн протяжённой антенной мало, предполагается, что характерный масштаб изменения функции f ( z ) много больше длины поперечной волны в массиве.

Опуская промежуточные выкладки, представим выражение для S_V в виде:

SV

+“

=iA J

—^

A(a72 -{2 ) H02l(c№| h     hpc о Ti—?21

ф ^ К ^{1 i} d i

где Ф ( , | — интегральное Фурье преобразование от f ( z | ,

• = =Д, na⁴ ■fi—i — —Ц² 7 b 2 — i ² + 4 H ^W a ²^, i ² x

c о           H j%7XF|Г

• #-^ Ja^ 4b² —, + 4 ^H 4⁰ ^- | 2¹ ( a 72— , ²1 ² 4b² —, , h г Vо pi — i

A = N 1 ( c о 7 Ь ² — , ² 1 / о ( c о 7 b ² — i ² 1 — N о ( c о 7 b ² — i² J 1 ( c о 7 b ² — i ² |} B ,

A i = V о ( c о 7 b ² — i ² У — N о ( c о 7 b ² — i² к} B,

B = N 1 c о 7 b ² — i ² к — J 1 ( c о 7 b ² — i У ,

I = J 1

—

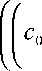
X

b

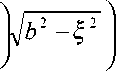
p fcfb iZjb — i2

Л

J ₀

I c о kv

—

X

b

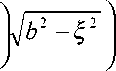
У = N i | c ₀ vv

—

X

—

b

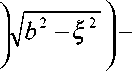
p f ^c f ^b

Zi

N о

c ₀

vv

—

X

b

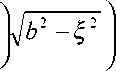
a ² n U _о n ^{n bc} f Z_m

p f       cci

П = —, a =   , b =

Ps       ct

= ^k l r 2 , c = ^k l r , c 1 = ^kz ,

X

X = kf ^{( r} 2 - ^r 1 ^| , С о -- = kr . b

Анализируя выражение (7) и действуя аналогично [ 4] , можно получить приближённые условия резонансного прохождения акустического поля, создаваемого скважинной пьезокерамической антенной, в массив. Условия эти накладываются на волновую толщину слоя жидкости X , находящегося между скважинной антенной и внутренней стенкой скважины, для простоты скважина считается необсаженой. Сформулировать эти условия можно с помощью следующего выражения:

X ( X ^{| = N} 1 ^{( c} о ^{b 1 J} 1 ^{( c} о ^b — X ^{| —}

^p f ^c f iZ m

^J о ^{( c} о ^b — X)

—

^J 1 ^{( c} о ^{b | N} 1 ^{( c} о ^b — X ^{| —} ff-m

^N о ^{( c} о ^b — X)

Резонансное прохождение акустической энергии от пьезокерамической протяжённой скважинной антенны через жидкий слой в массив должно наблюдаться при тех значениях X , при которых модуль | X ( x | из (8) принимает минимальные значения.

Зададимся конкретным типом протяжённой пьезокерамической антенны, например, из [8] и исследуем условия резонансного прохождения акустической энергии от данной антенны в массив в зависимости от диаметра скважины. Антенна состоит из пьезокерамических цилиндров с внешним диаметром 74 мм, внутренним 66 мм и высотой 30 мм, сделанных из пьезокерамики со следующими характеристиками: cE =3500 м/с; d31 = 1,95 • 10 1л Кл/Н; s 1E1 = 11,3 -10-12 м2/Н; pc = 7,2 -103 кг/м3, погонная ёмкость у антенны Ca ~ 0,45 мкФ/м. Исходя из эквивалентной схемы, изображённой на рис. 3б, получим выражение для удельного механического импеданса антенны:

^Z m = r ml + i ^d 1

P fcf   P fcf   P fcf где d 1 = pccE

2nf8

c E

I c ¹

^^^^^^^^

8      + ^{2 n}P c ( c E ) 2 ^d 321

WCffi (f E y_aC_a

\

J

Основной проблемой в расчётах является корректное определение величины ( r_ml / P f c f ) см., например, [ 9] . Значительные проблемы возникают, если предполагается использование антенны под значительным статическим давлением (десятки МПа). Величина r_ml существенно зависит от внешнего давления и измерение её, если это необходимо, нужно проводить под рабочим давлением, при этом следует учесть, что величины d ₃₁ и s ₁ ^E ₁ также имеют зависимость от внешнего давления. В нашем случае протяжённая (длиной около 5 метров) антенна использовалась при избыточном давлении не более 0,5 МПа в среде, по своим характеристикам близкой к воде [ 8] . При проведении дальнейших оценок для рассматриваемого случая будем пренебрегать влиянием внешнего избыточного давления и его изменениями вдоль протяжённой антенны. В принципе, величину ( r_ml /р_fc_f ) можно грубо оценить из измерений в воде электроакустического к.п.д. n ea при работе на резонансной частоте антенны: ⁽ r ml/ P f c f Ы¹/ П еа ^- 1 ) ^[ 10] - При этом необходимо предположить, что появление скважины не изменяет существенно интегральные механические потери в конструкции антенны, а касается лишь активной и реактивной составляющих сопротивления излучения. Резонансная частота антенны в скважине, которая является одной из нормальных частот системы из двух связанных колебательных систем, ниже, чем собственная резонансная частота антенны в воде. Следовательно, для корректного определения величины ( r_ml /р f c f ) необходимо знать частотную зависимость этой величины, которая может быть определена при исследовании, например, частотной зависимости давления, создаваемого протяжённой пьезокерамической антенной в воде. Легко видеть, что давление P , измеряемое в воде на некотором расстоянии R от антенны, можно записать в виде:

р, cnUJr/R ww 1

“   Zm + Z ’ где Zl — эквивалентное сопротивление излучения протяжённой цилиндрической антенны в воде; Zl = (а + ifi )pwcw (см., например, [9]), а ив — безразмерные коэффициенты при составляющих сопротивления излучения, pw и cw — соответственно плотность и скорость звука для воды. Окончательно, выражение (9) приобретает следующий вид:

P =_____ nUJrJR _____

^{( r} mi l^pP c W ^{) + а ) +} i ⁽ d 1 ^{+ в )} '

На рис. 4 показана величина ( r_ml / p _wc_w ) для антенны из [ 8] , измеренная таким образом.

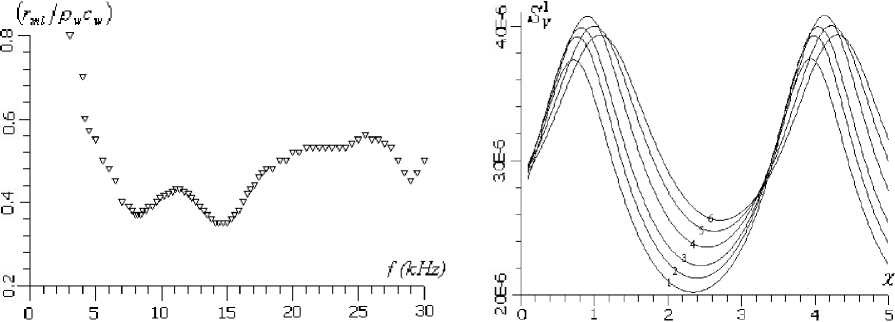
Рис. 4.                                           Рис. 5.

Пользуясь экспериментальными данными и выражениями (7), (8) можно получить оптимальные условия прохождения акустической энергии в массив от рассматриваемой скважинной антенны, работающей на разных частотах, в зависимости от параметра х .

На рис. 5 представлено поле объёмных деформаций SV1 на расстоянии 1 метр от оси скважины, полученное с помощью выражения (10) для исследуемого случая. Кривая 1 соответствует частоте излучения антенны f = 15,7 кГц; 2 — f = 15,2 кГц; 3 — f = 14,7 кГц; 4 — f = 14 кГц; 5 — f = 13,3 кГц; 6 — f = 12,8 кГц. Для расчёта взяты параметры из [8]: п = 0,5, a = 2,11, b = 1,27, U0 = 300B, в качестве жидкости, находящейся в скважине, предполагается вода. Резонансная частота антенны, измеренная в воде frews=14,7 кГц. При работе антенны в скважине максимальная амплитуда объёмных деформаций в околоскважинном пространстве создаётся на частоте f^=14 кГц, при значении хГes =0,9, XL - хГes ^ п . При отходе от f^s падает амплитуда SV и изменяется параметр хГes, соответствующий оптимальному прохождению акустической энергии в массив. На рис. 6 представлено сравнение значений хГes, полученных из выражений (7) (зависимость 1) и (8) (зависимость 2), при работе антенны в районе своей резонансной частоты. Хорошо видно, что отличие значений /Гes, полученных из разных выражений, менее 10%, что вполне приемлемо для практики.

Таким образом, формулой (8) можно пользоваться для оценок оптимальных условий излучения различных протяжённых антенн, находящихся в рамках эквивалентной схемы, изображённой на рис. 3б.

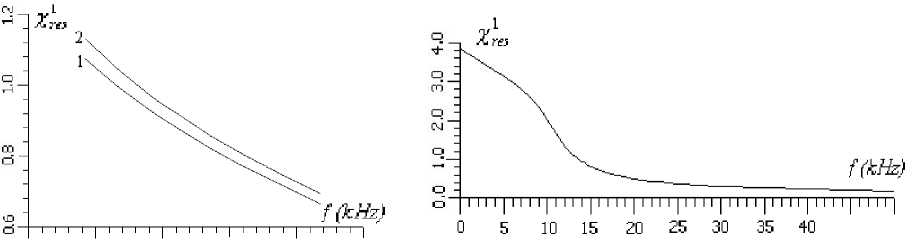
12       13       14       15       16       17

Рис. 6.                                           Рис. 7.

На рис. 7 на примере рассматриваемой антенны представлена эволюция /Гes в зависимости от частоты возбуждения протяжённой антенны. Зависимость получена с помощью выражения (8). При уменьшении волнового размера kr1 происходит переход к известной задаче об излучении точечного источника в скважине [13], где выполняется условие J 1 (хГes )ч 0 (/Гes ч 3,82) см. рис. 7.

Эквивалентная схема на рис. 3б является справедливой для работы цилиндрического преобразователя вблизи низкочастотного радиального контурного резонанса. Тем не менее, выражение (8) описывает закономерное стремление /Г es к нулю при увеличении относительных волновых размеров стенки излучающего цилиндра (см. рис. 7), т. е. качественно описывается предельный переход к задаче, рассмотренной в [3, 4].

К сожалению, на практике чаще всего геометрические характеристики скважины и акустических антенн заданы заранее и не являются оптимальными. Случайные соответствия, как, например, в случае [8], где решались задачи, связанные с акустической интенсификацией геотехнологических процессов, являются лишь исключениями. Протяжённая пьезокерамическая антенна в [8] работала в скважине с эффективным внутренним диаметром d2 «210 мм., который достаточно близко соответствовал параметру %^. Оптимальной же для данной антенны, с точки зрения прохождения акустической энергии в массив, является скважина с внутренним диаметром d2 ~ 100 мм., который соответствует параметру /Гes. Моделирование реальной ситуации, описанной в работе [8], с помощью выражений (3)–(6) даёт весьма близкое соответствие с экспериментальными данными [8], особенно при расчёте частот пропускания системы «протяжённая пьезокерамическая антенна – жидкий слой – массив».

ЗАКЛЮЧЕНИЕ

В настоящей работе рассмотрено излучение протяжённой некомпенсированной пьезокерамической антенны, находящейся в необсаженой скважине, которая заполнена жидкостью. Аналогичным образом можно рассмотреть задачу об излучении компенсированной антенны. Эквивалентную электромеханическую схему для записи граничных условий дифракционной задачи в этом случае можно получить следуя результатам работы [ 11] .

В скважинной акустике часто используются магнитострикционные модули для излучения акустического поля из скважины [ 14] . В принципе, на их основе можно создать протяжённую скважинную антенну. Эквивалентные электромеханические схемы магнитострикционных излучателей известны [ 9] и их также можно использовать для определения реальных граничных условий при решении дифракционных задач. Метод получения граничных условий на излучающей поверхности будет аналогичен представленному в данной работе. Не представляет труда обобщение приведённого выше решения задачи на случай излучения акустической энергии из скважины в массив через обсадную колонну и закрепляющее её цементное кольцо, дополнительные к (3) граничные условия для такой многослойной коаксиальной системы выписаны в [ 15] .

Работа выполнена при поддержке РФФИ, проект 03-02-16805 и гранта Минобразования Е02-8.0-58.