Об особенностях расчетно-экспериментальных исследований аэродинамических процессов при гиперзвуковых скоростях обтекания

Развитие современной техники, наряду с возрастающими требованиями надежности образцов ракетно-артиллерийского вооружения, изделий космической и других отраслей, ставит задачи моделирования и экспериментального исследования физических процессов, связанных с их эксплуатацией. Одной из таких проблем является увеличение скоростей полёта объектов, что вызывает необходимость корректного моделирования, оценки возможности и методической отработки проведения их аэробаллистических испытаний при сверхзвуковых и гиперзвуковых скоростях обтекания.

Корректное моделирование физических процессов, сопровождающих гиперзвуковой полёт тела, — фундаментальная задача аэродинамики. Часть экспериментальных результатов, полученных по данной тематике, обсуждалась в [1]. Основная методическая особенность проблем аэродинамики больших скоростей заключается в сложности их экспериментального моделирования. Этим и объясняется ситуация, что теоретические исследования значительно опережают экспериментальные достижения по уровню и глубине. Основные положения теории гиперзвуковых течений представлены в [2].

В настоящей работе приводятся результаты экспериментов, осуществляемых с помощью современного гиперзвукового аэробаллистического оборудования, которые можно рассматривать как постановочные с точки зрения оценки возможности экспериментального исследования проблем гиперзвуковой аэродинамики в лабораторных условиях.

Используемая аэробаллистическая установка включает два основных элемента: легкогазовое метательное устройство (МУ) и измерительную трассу полета объектов — аэробаллистический тир (АБТ), общей длиной L = 160 м. МУ и начальный участок трассы полета ( L = 36 м) находятся на открытой местности, а основной участок трассы (АБТ), — в закрытом затемненном сооружении (Рис. 1).

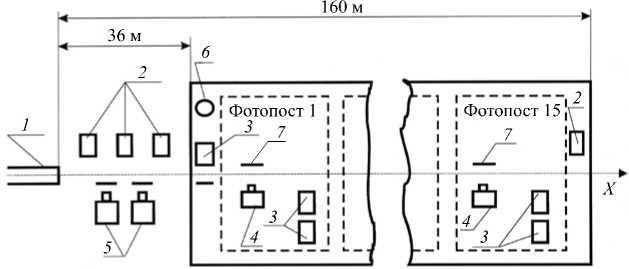
Рис. 1. Состав и типовая схема расстановки оборудования в аэробаллистической установке: 1 – метательное устройство (МУ), 2 – рентгеновские аппараты (РА), 3 – импульсные источники света ( ИИС), 4 – аэрофотоаппараты (АФА), 5 – электроннооптические фотокамеры (ЭПОС), 6 – синхро-баллистические фотокамеры (СБФ), 7 – экраны

АБТ представляет собой измерительную трассу, оснащенную 15 фотопостами, равномерно расположенными вдоль закрытого участка траектории полета объекта. В состав штатного фотопоста входят 2 аэрофотоаппарата (АФА) с фокусом 100 мм и до 4 импульсных источников света (ИИС), способных в момент фоторегистрации давать световые вспышки длительностью t _эксп = 4 мкс. Схема местоположения регистрирующей аппаратуры фотопоста предусматривает проведение конвергентной фотосъемки с вертикальным базисом 4,5 м. Фотопост обеспечивает воспризведение на одном снимке в масштабе 1 : 50 до четырех положений объекта с шагом через 1,5 м на участке траектории полета 8 м с трубкой разброса траектории до 0,3 м. В зависимости от целей испытаний фоторегистрация может проводиться или в отраженном свете, или быть силуэтно-теневой [3, 5]. В первом случае фон снимка черный, во втором — белый. Управление работой оптико-фотографической аппаратуры АБТ осуществляется с помощью автоматизированной системы на базе ЭВМ в реальном масштабе времени с учетом измеренной реальной скорости движения.

На открытом участке трассы и в АБТ размещаются рентгеновские аппараты мягкого излучения (РА), синхро-баллистические (СБФ) и электронно-оптические (ЭПОС) фотокамеры, позволяющие в совокупности повысить информативность и качество опытной информации. При этом электроннооптическая камера производит фотоснимки с длительностью экспозиции до 1 мкс, что важно для высокоскоростных режимов испытаний, а синхро-баллистическая фотокамера производит фотосъемку на движущуюся пленку. При хорошей синхронизации получаются четкие снимки, без искажений вследствие смазывания изображения. Регулируя ширину щели затвора СБФ, можно добиться продолжительности экспозиции ® 10 мкс.

В описываемых экспериментах ширина щели СБФ равнялась 34 мм, что при ширине пленки 70 мм обеспечивало зону регистрации 2,8 х 1,5 м. В этих условиях длительность экспозиции для самосветящихся объектов, определяемая скоростью увода изображения из кадрового окна, составляла ® 0,5 мс, а для его теневого изображения равнялась длительности воздействия импульсного источника света (ИИС) ( ® 4 мкс). Фотосъемка с помощью АФА и СБФ осуществлялась на фоне белых экранов с целью реализации способа силуэтно-теневого фотографирования. При этом АФА, фактически, работали в ждущем режиме, и самосветящиеся объекты, в этой связи, регистрировались в виде световых треков. На этих же снимках, в случае срабатывания ИИС, фиксировались как изображение объектов испытаний в отраженном свете (если по яркости оно превосходило самосвечение), так и их теневое изображение. Фотокамера ЭПОС снимала в проходящем свете, то есть камера и источник света располагались по разные стороны экрана, на котором строилось изображение регистрируемого объекта. Длительность экспозиции в этом случае, как уже отмечалось, составляла ® 1 мкс и равнялась продолжительности работы оптико-электронного затвора.

В постановочных опытах на аэробаллистической установке основными объектами испытаний являлись шары диаметром 10,4 мм и массой 10 г, изготовленные из вольфрама, никеля, железа — ВНЖ-90 (опыт № 4), и шары диаметром 10,4 мм и массой 11,5 г из высокопрочного сплава ВР (опыты № 1 ^ 3). Шары отстреливались в свободный полет с начальными скоростями V : 3,86 км/с (опыт № 1); 4,70 км/с (опыт № 2); 5,07 км/с (опыт № 3); 5,8 км/с (опыт № 4) с помощью МУ (легкогазовой баллистической установки); дальность свободного полета составляла порядка 160 м. В течение полета производились оптические, рентгенографические и хронографические измерения. Начальная температура объектов соответствовала метеоусловиям на момент проведения опытов (10 + 20 °С).

При увеличении начальных скоростей полёта у шариков из высокопрочного сплава ВР наблюдалось повышение яркости трека: на снимках с камер комбинированного фотопоста, производивших съемку в отраженном свете, более заметным становился видимый след за объектом исследования. Результаты оптических, рентгенографических и хронографических измерений, полученные при проведении опытов № 1 ^ 3, более подробно описываются в [1].

ВНЖ-90 — композитный материал. В отличие от сплавов стали его структура неоднородна, так как материал создается методом порошковой металлургии — спеканием компонент при определенных условиях. Основой служат зерна вольфрама (90% по массе) размером 70 ^ 200 мкм, скрепленные пленкой расплава железо–никель.

В процессе полета под действием аэродинамического теплового потока (конвективного и излучаемого) происходит интенсивный нагрев лобовой поверхности объектов. Здесь температура достигает температуры разрушения материала, и обтекающий газовый поток начинает уносить материал, что обуславливает изменение массы и обводов объекта. По мере торможения тепловые потоки снижаются, прекращаются унос и изменение обводов объектов, падает температура поверхности. Отмеченные обстоятельства наблюдаются во всех проведенных экспериментах.

На рисунке 2 представлены результаты регистрации фотокамерами АФА полета шарика из ВНЖ на участке траектории, где происходит унос материала. Характерным является наличие плотного трека светящегося шарика в ореоле расходящихся треков светящихся частиц, имеющих значительно меньшие размеры.

Рис. 2. Регистрация камерой АФА полета шарика из ВНЖ на участке траектории, где происходит унос материала ( X = 66 м, V « 4 км/с)

Показанные на рисунке 3 рентгеновские снимки различных стадий полета этого шарика позволяют предложить качественную картину процессов, в том числе, и регистрируемых фотокамерами АФА. По мере уноса материала на рентгеновских снимках в зоне лобовой поверхности шарика вверх по потоку регистрируется затемненная область с размытой границей. Судя по характеру границы, эта область заполнена газом и распространяется вниз по потоку до окрестности точки начала резкого расширения потока (Рис. 3). Наличие указанной области обусловлено особенностями процесса аэротермомеханического уноса ВНЖ и аэробаллистическими условиями полета. Как уже отмечалось, ВНЖ представляет собой композитный материал, и его компоненты имеют отличающиеся теплофизические свойства, в частности, температуру плавления. В этой связи, по мере разогрева лобовой части шарика, первой достигается температура плавления связующего звена железо–никель, которая примерно в 2 раза ниже температуры плавления основы — зерен вольфрама. В результате плавления связки зерна вольфрама или их отдельные ассоциации теряют механическую связь между собой и начинают автономное движение в ударном слое. По рентгеновским снимкам видно, что торможение шарика оказывается более интенсивным, и поэтому в относительном движении зерна вольфрама продвигаются вверх по потоку относительно твердой поверхности шарика. Начав автономное движение в ударном слое совместно с газовой фазой, омывающей твердую поверхность, они приобретают составляющую скорости, нормальную к поверхности шара. В этой связи их траектории отклоняются от траектории шарика и формируют ореол треков, регистрируемых фотокамерами АФА.

Рис. 3. Рентгеновские снимки шарика из ВНЖ в различных стадиях полета: X = 14 м, V = 4,9 км/с ( а );

X = 26 м, V = 4,6 км/с ( б ); X = 43 м, V = 4,1 км/с ( в ); X = 156 м, V = 1,5 км/с ( г ) (направление полета слева направо)

Снимки, выполненные в этих же условиях электронно-оптическими фотокамерами ( t _эксп ® 1 мкс) в проходящем свете (Рис. 4), свидетельствует, что зерна вольфрама практически равномерно распределяются в зоне, охватываемой головной ударной волной вниз по потоку. Они регистрируются на фотоснимке, поскольку их полет, вероятно, сопровождается теми же световыми явлениями, что и полет шарика в целом. Воздух, протекающий через близкую к прямолинейной часть головной ударной волны, имеет высокую температуру и формирует на снимке яркий светящийся след, поперечный размер которого близок к диаметру шарика. При этом для проходящего света след остается прозрачным, поскольку теневая картина течения, регистрируемая на этом же снимке, не имеет очевидных отличий от аналогичных, регистрируемых при гиперзвуковом полете (при числах Маха M >  6) неразрушающихся тел. Плотность частиц в объеме, охватываемом хвостовой частью головной ударной волны, и их размеры настолько малы, что не регистрируются на рентгеновских снимках (Рис. 3) и теневой картинке течения (Рис. 4).

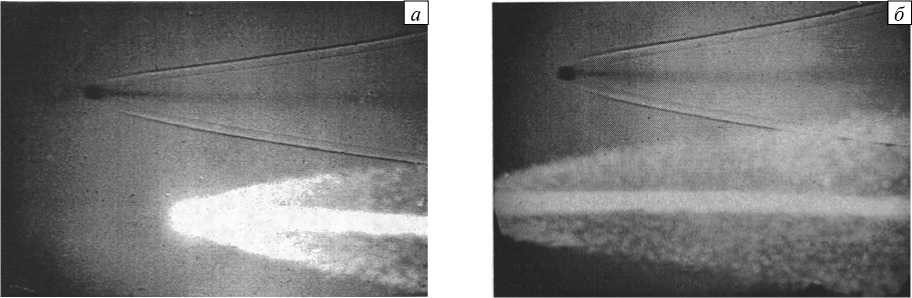
Рис. 4. Регистрация полета шарика из ВНЖ двумя камерами ЭПОС на участке траектории, где происходит унос материала ( X « 14 4- 20 м, V = 4 км/с)

Зависимости коэффициента силы лобового сопротивления C_x от числа Маха M для шаров, изготовленных из разных конструкционных материалов, представлены на рисунке 5. При отсутствии уноса материала (опыты № 1 ^ 3) графики соответствуют «классическим» представлениям и практически постоянны в пределах погрешности эксперимента во всем реализованном скоростном диапазоне. В опыте № 4 зависимости C_x (M) имеют больший градиент, что является косвенным доказательством наличия аэротермомеханического разрушения конструкционных материалов объектов испытаний, сопровождающегося существенными изменениями геометрии и массы последних ( ~ 10 ^ 15%).

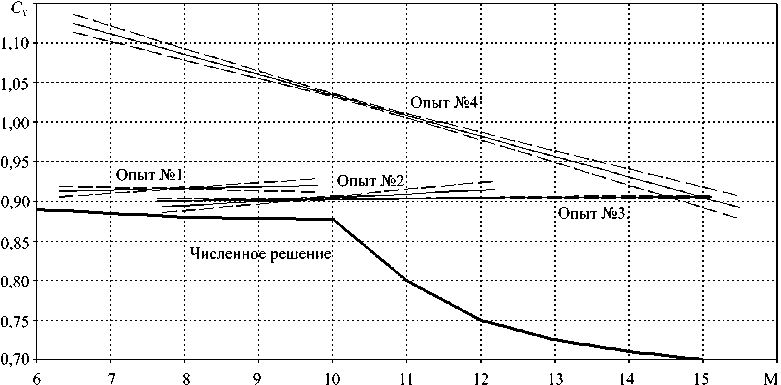
Рис. 5. Зависимость коэффициента силы лобового сопротивления ( C _x ) от числа Маха ( M ) для шаров из различных конструкционных материалов

С точки зрения уточнения математических моделей процесса мелкодисперсного дробления чрезвычайно важными могут оказаться факты, зарегистрированные при испытаниях шарика из ВНЖ. В первую очередь имеется в виду зарегистрированный на рентгеновских снимках унос частиц вольфрама в лобовой зоне вверх по потоку от твердой поверхности шарика (Рис. 3). В имеющихся математических моделях полагается, что дробленая масса (мелкие частицы), обладая значительной деформируемостью, становится близкой по свойствам к жидкости, и поэтому возможность распространения частиц вверх по потоку даже не обсуждается. В то же время присутствие этих частиц в ударном слое может оказать существенное экранирующее воздействие, по крайней мере, на уровень тепловых потоков (конвективного и излучаемого. В этой связи может потребоваться уточнение математических моделей мелкодисперсного дробления в части учета аэробаллистических аспектов относительного движения частиц и основного тела.

Совокупность фактов, зарегистрированных при проведении постановочных экспериментов, относится главным образом к аэротермомеханическим и баллистическим аспектам движения тел при гиперзвуковых скоростях обтекания. Найденные результаты свидетельствуют, что аэробаллистический метод может быть достаточно эффективным инструментом исследования данных процессов.

Для отработки методик расчета с помощью современных инженерных методов компьютерного моделирования процесса гиперзвукового обтекания произведен расчет моделей при различных скоростях обтекания. Объектом моделирования служил шар диаметром 10,4 мм. В качестве метода моделирования был выбран метод численного решения осредненных по Рейнольдсу уравнений Навье–Стокса, дополненный k -s -моделью турбулентности. Этот метод реализован в современном инженерном программном пакете COSMOSFloWorks [4].

Пакет представляет собой комбинацию полной версии системы SolidWorks как графической среды и гидрогазодинамического решателя COSMOSFlow, препроцессор которого позволяет реализовывать автоматизированный или ручной метод блочного построения расчетной сетки и ее последующей адаптации в зонах больших градиентов параметров потока. Пакет COSMOSFloWorks предусматривает решение пространственных трехмерных задач внешнего сверхзвукового обтекания твердых тел с учетом вязкости, теплопереноса, шероховатости поверхности объекта, степени турбулентности потока. В результате решения могут быть установлены аэродинамические силы и моменты, действующие на обтекаемую поверхность объекта, вычислены все параметры обтекающего газа в расчетном объеме — поля давлений, плотностей, температур, скоростей. Полученные результаты могут выводиться в виде контурных распределений параметров течения в объеме и на поверхности тела, а также соответствующих графиков для любого выбранного сечения.

Для определения влияния размеров расчетного домена на характер обтекания шара и коэффициент лобового сопротивления проанализировано несколько доменов различных размеров при одной начальной скорости обтекания (M = 6). Исходя из условий симметрии была взята лишь четвертая часть полного, окружающего весь шар домена. Расчетный домен, используемый в дальнейших исследованиях влияния начальной скорости потока на коэффициент лобового сопротивления и на характер обтекания шара, имеет размеры 90 х 50 х 50 мм.

Задача рассматривается в трехмерной постановке, поскольку, во-первых, данные расчеты предваряют моделирование конструкций со щитковыми органами управления, характеризующихся сложной картиной обтекания, и служат для отработки выбранного расчетного домена, а во-вторых, особенность используемого пакета заключается в том, что двухмерные осесимметричные задачи решаются в них в трехмерной постановке.

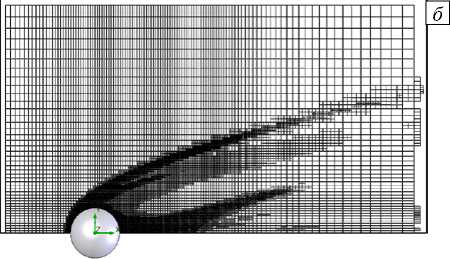
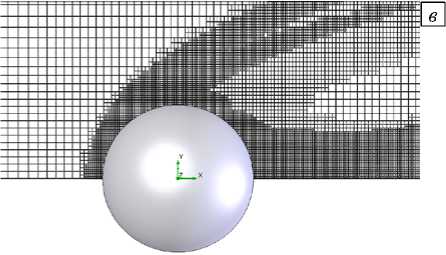
На рисунке 6, а , б приведена исходная сетка для расчетов обтекания модели, а также показана дважды адаптированная после 13 80 и 2070 итераций сетка для условий обтекания с начальной скоростью M = 7.

в

Рис. 6. Исходная ( а ) и адаптированная ( б ) расчетная сетка при M = 7; фрагмент адаптированной сетки ( в )

Исходная сетка состоит из 234963 ячеек, а адаптированная сетка — из 381676 и 801067. На рисунке 6, в фрагмент адаптированной сетки для условий обтекания с начальной скоростью M = 7 показан в увеличенном масштабе.

Трехмерный расчет процесса внешнего обтекания шара сверхзвуковым потоком сжимаемого газа проводился с учетом соответствующих граничных условий на поверхности шара и на стенках расчетного домена. Решались полные, осредненные по Рейнольдсу уравнения Навье–Стокса, дополненные двухпараметрической моделью турбулентности с установленными по умолчанию параметрами. Диапазон рассмотренных начальных скоростей обтекания составлял 6 л 15M . Для воздуха использовалось уравнение состояния совершенного газа. В процессе расчета определялись полные в объеме домена поля для всех параметров обтекающего газа: численно находились значения коэффициента лобового сопротивления шара (зависимости от числа Маха показаны на рисунке 5), характер обтекания шара (при начальной скорости M = 7 на рисунке 7 изображены соответствующие параметры). Из рисунков можно заметить, что характер обтекания и вычисленные значения коэффициента сопротивления в зависимости от чисел Маха в целом соответствуют экспериментальным данным, ранее приведенным в различных источниках [3, 5, 6, 7].

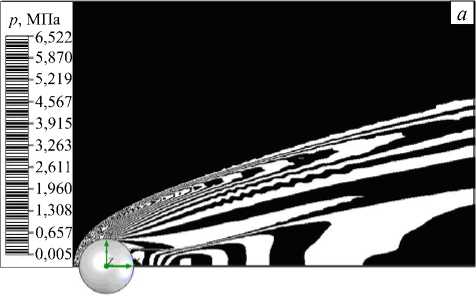
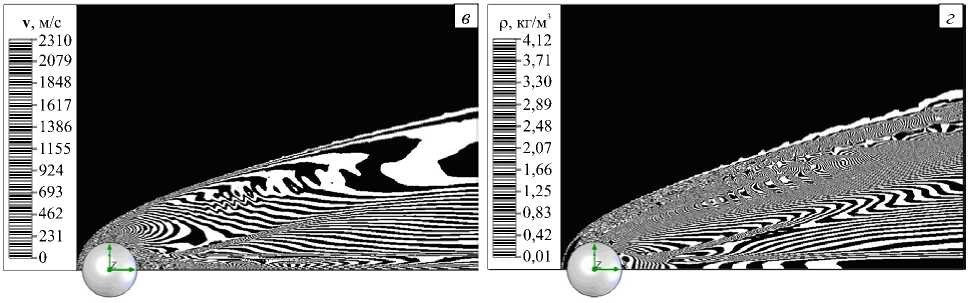
Рис. 7. Распределение полей давлений p , МПа ( а ), температур T ,K ( б ), суммарных векторов скоростей v , м/с ( в ) и плотностей р , кг/м³ ( г ) в потоке при обтекании шара с начальной скоростью M = 7

Расчеты с начальными скоростями более M = 10 показали, что при обтекании происходит нарушение алгоритма автоматической адаптации расчетной сетки, возникает проблема получения устойчивого решения, что влечет за собой некорректное вычисление значений коэффициента лобового сопротивления и характера обтекания шара в целом. На рисунке 5 отлично видно огромное отличие результатов численного моделирования от экспериментальных данных. Кроме того, при столь высоких скоростях обтекания возможен процесс аэротермомеханического разрушения шара вследствие сопровождающих процесс обтекания химических реакций, уноса материала и изменения формы шара, ионизации. Наличие вышеописанных явлений требует существенной корректировки математической модели. Тем не менее, сопоставление результатов при скорости не выше M = 10 позволяет сделать вывод о возможности использования модели в этом диапазоне.

В результате выполнения работы произведены эксперименты с целью оценки возможности и методической отработки проведения аэробаллистических испытаний для исследования процессов гиперзвукового обтекания конструкций. В ходе экспериментов тела простой формы (шары, изготовленные из различных конструкционных материалов) метались со скоростями V = 3,86 л 5,8 км/с. Для такого вида изделий показан характер обтекания, построены зависимости коэффициента аэродинамического сопротивления от числа Маха при различных начальных скоростях полета. С применением оптического и рентгенографического измерительных комплексов зарегистрирован ряд явлений, сопровождающих процесс обтекания. Их анализ показал правомерность аэробаллистического метода как инструмента для исследования широкого круга проблем гиперзвукового обтекания тел. Численное моделирование осуществлялось в инженерном программном пакете COSMOSFloWorks.