Об относительности меры нелокальности в квантовой механике

В квантовой механике (КМ) хорошо известен феномен так называемого “отложенного выбора”. Соответствующая парадигма в виде мысленного эксперимента была предложена Дж. Уилером и подытожена им в работе [1]. Целью было исследование дуалистического (корпускулярноволнового) поведения квантовых частиц, и ряд этих экспериментов впоследствии с успехом был осуществлен на практике (см. обзор [2]). С одной стороны, экспериментатор мог легко варьировать конфигурацию эксперимента так, чтобы “навязывать” квантовой частице корпускулярный или волновой сценарий поведения, что проявлялось в отсутствии или наличии интерференции на выходе интерферометра. С другой стороны, парадоксальным образом казалось возможным делать этот выбор иотложенным,,5 т.е. осуществлять его “задним чиcлoм^^ - после завершения самого эксперимента, что немедленно порождало естественные вопросы о нарушении причинности и связанных с этим парадоксах.

В процессе анализа неизбежно всплывала и т.н. проблема квантовой нелокальности (ипри-зрачного действия на paccтoянии^^ по Эйнштейну). Исследуя ее теоретически и экспериментально, авторы работ [3-6] проверяли (см. ниже раздел 3), влияет ли выбор системы отсчета на корреляции состояний удаленных запутанных частиц, и приходят к убеждению, что ^окончательные результаты экспериментов с движущимися измерительными устройствами исключили возможность описания квантовых корреляций с помощью реальных часов, в терминах "раньше"и ппозжеп; феномен квантовой нелокальности не может быть описан в терминах пространства и времени. Это означает, что для нелокальных корреляций отсутствует упорядочение во времени, так что причинный порядок не может быть сведен к упорядочению во времени” [4]. См. также [7].

К такому же выводу теоретически приходит и автор [8]. Он предлагает теоретический анализ парадоксов Эйнштейна-Подольского-Розена [9] и отложенного выбора на основе расчета условных вероятностей состояний запутанных частиц. Впрочем, мы не исключаем, что приведенное в его работе доказательство содержит скрытый ^порочный круг” ， априорно подразумевая симметрию измерений над различными частицами.

Ниже мы предлагаем собственное решение указанных проблем применительно к характерным экспериментам с квантовыми частицами, основанное на известном парадоксе часов теории относительности.

1.    Парадокс часов для экспериментов с запутанными фотонами

Рассмотрим разлет двух частиц, например, ракет 一 из общего центра. Пусть ракеты движутся во взаимно противоположных направлениях и обладают одинаковой по абсолютной величине скоростью 仏 с которой они удаляются от неподвижного центра разлета (система отсчета К> Перейдем теперь к движущейся системе отсчета К2, жестко связанной с одной из ракет; очевидно, в этой новой системе отсчета данная ракета будет неподвижной, а другая ракета будет удаляться от нее со скоростью и = 2。(в иерелятивистском приближении). Если же скорость удаления достаточно велика, то скорость взаимного удаления должна вычисляться по известному правилу теории относительности (см., например, [10]), т.е. в данном случае будет равна и = 2。/(1 + и2/с2), г де с -скорость света в вакууме. В пределе эта итоговая скорость взаимного удаления будет стремиться к с даже если одна, из ракет по какой-либо причине прекратит свое движение отпосителыю неподвижного центра.

По мере приближения скорости взаимного удаления ракет u к скорости света собственное время удаления и собственное расстояние, на которое другая ракета удаляется, сократятся в соответствии с релятивистским множителем 7 = ， 1 - и²/с² и в пределе будут стремиться к нулю. Иначе говоря, согласно теории относительности, для летящих (в том числе - разлетающихся) со скоростью света фотонов расстояния и отрезки времени не существуют. То, о чем мы говорим, по существу представляет собой хорошо известный в теории относительности парадокс часов. Он проверен экспериментально, в том числе - на примере реальной работы глобальной системы навигации GPS [11].

2.    ЭПР-эксперименты

Одним из наиболее известных парадоксов квантовой теории, сформулированным еще в знаменитой статье [9], является наличие корреляций между состояниями двух достаточно удаленных запутанных частиц. Белл [12] в 1964 году вывел неравенство, которому должны удовлетворять эти корреляции в случае обычных (классических) частиц, связанных общим прошлым. Однако он же показал, что это неравенство при некоторых условиях может нарушаться в квантовой механике. В дальнейшем это было многократно подтверждено экспериментами, начиная с работ группы Аспэ [13].

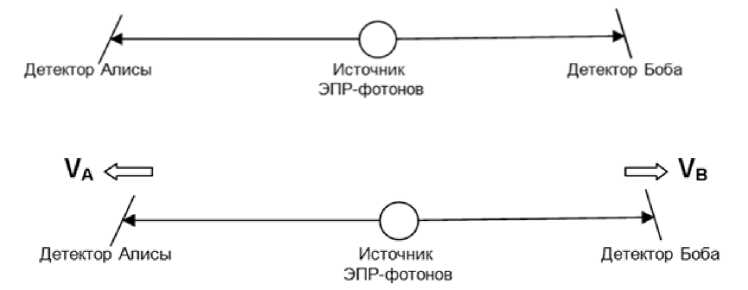
Рис. 1. моменты времени регистрации фотонов определяются: в одной и той же лабораторной системе отсчета (оба детектора неподвижны; сверху) в двух различных системах отсчета, связанных с соответствующими детекторами (каждый детектор движется со своей скоростью; снизу)

На рис. 1 показана упрощенная схема типового ЭПР-опыта с фотонами. Общий источник излучает пару запутанных фотонов, поляризационное состояние которых может быть измерено Алисой и Бобом (каждый измеряет линейную поляризацию “своего” фотона). Степень корреляции состояний зависит только от разности углов между ориентациями поляризаторов, выполняющих роль детекторов. После эмиссии ЭПР-пары вплоть до измерений состояние фотонов считается неопределенным. При этом квантовая механика подразумевает (и это подтверждено — для лабораторной системы отсчета — многочисленными экспериментами с быстродействующим переключением поляризаторов, см., например, [13]), что измерение, выполненное в каком-либо месте, приводит к “мгновенному” воздействию на всю систему в целом (включая любую ее часть) и переводит ее в измеренное собственное состояние. Это означает, что, вообще говоря, даже если только Алиса (или только Боб) измерит поляризацию своего фотона, то и в этом случае состояние другого фотона мгновенно окажется определенным . При этом обычно по умолчанию подразумевается, что оба измерения проводятся в одной и той же лабораторной системе отсчета (где оба детектора неподвижны, рис. 1а), т.е. по единой шкале времени. А “частица, попавшая в измерительное устройство позже, может сподозреваться? в том, что она каким-то образом учитывает результат, полученный для ранее измеренной чacтицы^^ [4].

Впрочем, чтобы проверить корреляцию состояний фотонов (по результатам многократно повторенных экспериментов), все равно необходимо измерять состояния обоих фотонов, так что, с нашей точки зрения, допустимо предположить, что процедура измерения в данном случае подразумевает завершение обоих измерений над двумя фотонами.

Между тем, по ряду причин идеальная синхронизация измерений невозможна. Если считать, что “коллапс волновой функции^,5 (детерминированность состояния после измерений) обоих фотонов вызван уже первым по времени измерением, то возможны в общем случае другие инерциальные системы отсчета (где детекторы движутся с разными скоростями Va и Vb), отличные от лабораторной, причем в каждой из этих систем отсчета первым по времени может оказаться разное измерение (рис. 1). “Если каждое из измерительных устройств в собственной системе отсчета первым зарегистрировало фотон, мы имеем упорядочение типа раньше-раньше (before-before timing)^^ [4]. Спрашивается, могут ли так организованные измерения повлиять на корреляции или даже устранить их?

В работе [6] описан эксперимент, позволивший ответить на этот вопрос. В качестве эквивалента движущегося детектора-светоделителя использовался акустооптический модулятор (АОМ). Лазерный источник генерировал ЭПР-пары фотонов с длиной волны 1314 нм. Каждый из фотонов направлялся в “свой” интерферометр, использующий отдельный АОМ. Там он дважды (с помощью пары зеркал) пропускался через акустическую волну, после чего регистрировался с помощью соответствующего детектора. Эксперимент показал полное соответствие предсказаниям квантовой механики: картина корреляций никак не изменилась по сравнению со случаем неподвижных детекторов.

Между тем, выявленный нами в предшествующем разделе парадокс часов позволяет понять, что происходит: для второго фотона, удалявшегося от первого фотона со скоростью света, время путешествия “не течет55 и пройденное расстояние в пространстве “не увеличивается55, т.е. мера квантовой нелокальности для нашей системы фотонов, оказываясь величиной относительной, уменьшается до нуля. И это не кажущийся, а совершенно объективный феномен, идентичный реальной разнице в замедлении времени движущегося объекта по сравнению с неподвижным. Более того, только в лабораторной системе отсчета сохраняет смысл говорить о различии в моментах измерения над одним и другим запутанными фотонами: для них в действительности это всегда синхронные события, какими бы разновременными они ни казались в лабораторной системе отсчета. Собственно говоря, ЭПР-опыты являются прямым подтверждением этого факта.

3.    Эксперименты с отложенным выбором

Квантовая нелокальность ярко проявляется в так называемых экспериментах с отложенным выбором, создающих у лабораторного наблюдателя иллюзию, что результаты квантового эксперимента фиксируются (корректируются) уже после его завершения.

В мысленном эксперименте Уилера, представленном на рис. 2, квантовая частица поступает на вход интерферометра Маха-Цеидера [1]. Относительная фаза ф между двумя плечами интерферометра регулируется так, что с определенностью на выходе Do может регистрироваться частица. То есть интерференция будет полностью конструктивной на выходе Do и полностью деструктивной на выходе D> Такое измерение как будто ясно подчеркивает волновой аспект квантовой частицы.

Однако наблюдатель имеет возможность изменить вышеописанный эксперимент, в частности, путем удаления второго светоделителя интерферометра (показанного пунктиром). В этом случае он осуществит измерение типа ^который путь (which-path)^^. Фотон будет зарегистрирован в каждой моде с вероятностью 1/2, демонстрируя корпускулярное поведение.

Главная идея этого эксперимента - свобода выбора: какой эксперимент выполнять (т.е. либо интерференция, либо “который путь” ， волновой или корпускулярный объект) в тот момент, когда частица уже находится внутри интерферометра. Таким образом, частица не может знать заранее (например, благодаря скрытым параметрам) типа эксперимента, который будет проведен, поскольку этот выбор просто еще не был сделан до момента попадания фотона в интерферометр. Рассмотрим далее два наиболее убедительных, с нашей точки зрения, реально выполненных современных эксперимента с отложенным выбором.

3.1.    Эксперимент 2000 г.

Первый из них описан в публикации [14], упрощенная схема эксперимента приведена на рис. 3. ЭПР-пары фотонов генерировались неколлинеарно в любой из областей А или В нелинейным оптическим кристаллом бората бета-бария. В каждой паре фотон 1 распространялся направо и фокусировался с помощью линзы. Он попадал затем на детектор О 。， который был смонтирован на шаговом двигателе, обеспечивающего его перемещение по оси хО.

Фотон 2, распространяющийся влево, проходил через один, два или три светоделителя. Если пара генерировалась в области А, то фотон 2 должен был попасть в светоделитель BSA, где он с вероятностью 1/2 отражался или проходил. Если пара генерировалась в области В, то фотон 2 должен был попасть в светоделитель BSB, где он опять-таки с вероятностью 1/2 отражался или проходил.

В случае, если фотон 2 проходил через BSA или через BSB, он должен был регистрироваться детектором Оз ил и D4 соответственно. Детектирование детекторами Оз ил и D4 формировало информацию о выборе пути для фотона 2, тем самым формируя информацию о выборе пути для фотона 1 вследствие запутывания фотонной пары. При этом интерференция отсутствовала.

С другой стороны, при отражении в BSA или BSB фотон 2 продолжал свой путь до попадания в другой светоделитель BS с 50-процентном делением и детектировался одним из детекторов Di ил и О?. Это приводило к стиранию информации о выборе пути, которую нес фотон 2 и, следовательно, фотон 1 демонстрировал интерференционное поведение (рис. 4). Это подтверждало теоретическое предсказание.

Выбор - наблюдать интерференцию или нет - осуществлялся случайным образом фотоном 2, который либо отражался, либо проходил через светоделитель BSA или BSB. Фактически в эксперименте фотоны распространялись в основном коллинеарно, но расстояние от ВВО до BSA и BSB были примерно на 2.3 м (7.7 нс) длиннее, чем расстояние от ВВО до О°. Таким образом, после того, как Оо зарегистрировал фотон 1, фотон 2 еще продолжал двигаться к BSA или BSB, т.е. выбор в пользу одного из путей или движения по обоим путям был uoтлoжeнным^^ по отношению к регистрации фотона 1.

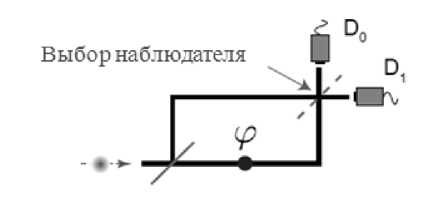
Рис. 2. Мысленный эксперимент Уилера с отложенным выбором [1]

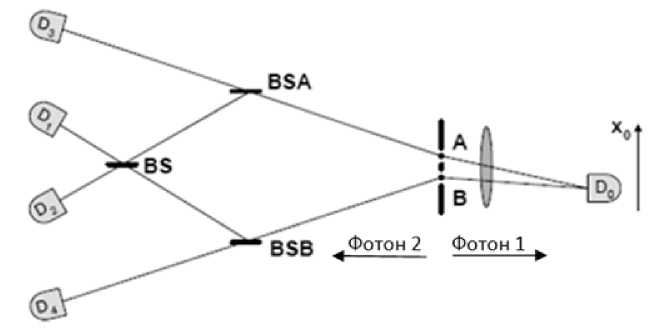
Рис. 3. Упрощенная схема эксперимента из [14]. Пара запутанных фотонов испускается атомом А или В в процессе атомного каскадного распада. Срабатывания детекторов & ил и D4 дают информацию о выборе пути, а срабатывания детекторов Di ил и D2 указывают на ее стирание (^икв антовый ластик"). BS, BSA, BSB - светоделители.

Возникающую иллюзию “нарушения прининности” мы предлагаем объяснить тем, что картина, в которой регистрация фотона 1 предшествует завершению регистрации фотона 2, наблюдается в лабораторной системе отсчета. Однако по отношению к удаляющемуся фотону обе частицы (в пределе скорости света) регистрируются синхронно, что приводит к корреляции отсчетов счетчиков совпадений.

3.2.    Эксперимент 2007 — 2008 гг.

Рассмотрим теперь более поздний эксперимент, описанный в [15]. В двух экспериментальных реализациях (Вена, 2007 и Канарские острова, 2008) источник запутанных фотонных ЭПР-пар испускал пару фотонов (^системный фотон” и ““отон сре^ы”). Системный фотон распространялся через интерферометр в одну сторону, а фотон среды являлся объектом поляризационных измерений с другой стороны от источника. Выбор вида измерения, позволяющий либо задать информацию о выборе пути (“а” или “Ь”), либо получить интерференционную картину для системных фотонов, делались в условиях локальности по Эйнштейну, т.е. причинная связь (в лабораторной системе отсчета) между системным фотоном и фотоном среды заведомо отсутствовала.

Целью этого эксперимента (его концептуальная схема приведена на рис. 5) являлась манипуляция типом поведения системного фотона с помощью измерительного воздействия на фотон среды. При измерении фотона среды в линейном базисе выявляется информация о выборе пути системным фотоном, при этом интерференция системного фотона наблюдаться не может; при измерении фотона среды в круговом базисе информация о выборе пути стирается, возникает интерференция системного фотона, которая зависит от сдвига фаз в плечах “а” и “Ь” (волновое поведение).

Если путь системного фотона (справа) до детекторов длиннее, чем путь фотона среды (слева) до коммутатора, то парадокса нет - событие манипуляции фотоном среды происходит раньше, чем на выходе интерферометра возникает или не возникает интерференционная картина, т.е. причина предшествует следствию. Однако в том случае, когда путь системного фотона (справа) до детектора делается короче, чем путь фотона среды (слева) до коммутатора, то в лабораторной системе отсчета возникает, как считают авторы работы [15], парадокс - событие манипуляции фотоном среды происходит позже, чем на выходе интерферометра возникает или не возникает очередной фрагмент интерференционной картины. Авторы [15] ссылаются на экспериментальные результаты, полученные ими в своей работе (в лабораторной системе отсчета).

W40

S83U ① pouo。

■?:)

0 _t------------1------------------------1------------------------1------------------------1------------------------ 1............^-............¹........................

0.0        0.5        1.0        1.5        2.0        2.5        3.0

D о Position (mm)

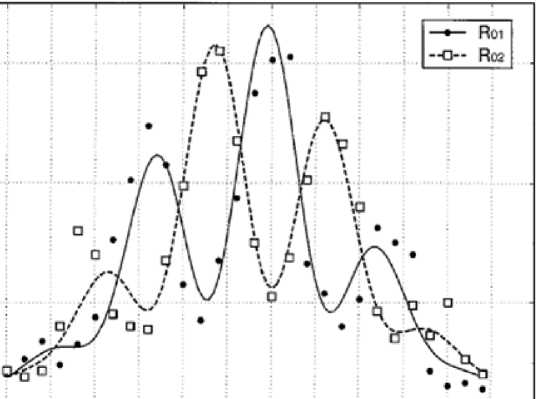
Рис. 4.  Roi (счетчик совпадений между Do и Di) и R02 (счетчик совпадений между Do и D2) в за висимости от координаты х детектора Do. Наблюдаются стандартные образцы интерференции Юнга на двух щелях. Фазы кривых отличаются на тт; если кривые просуммировать, то интерференционная картина исчезает.

С нашей точки зрения, парадокс устраняется так же, как и в предыдущих случаях, т.е. основан на некорректности использования лабораторной системы отсчета К* если же рассмотреть события относительно удаляющегося фотона, то промежуток времени (и расстояние) между измерениями над системным фотоном и фотоном среды будет стремиться к нулю, поэтому никакой рассогласованности в том, что с ними происходит, просто не может быть. Выходной бит генератора случайных чисел в этот момент времени связан с воздействием на фотон среды ровно таким сигналом, какой и должен быть, поэтому вся триада оказывается скоррелированной.

4.    О распространении гипотезы на частицы с ненулевой массой

До сих пор речь шла только о таких частицах, как фотоны, не обладающих, как известно, массой и распространяющихся со скоростью света. С первого взгляда кажется, что для массивных квантовых частиц (например, электронов) все сделанные выше утверждения неприменимы. На самом деле удивительным образом оказывается, что и в случае квантовых частиц с ненулевой массой в некотором смысле можно (и нужно) говорить о световых скоростях распространения (см. нашу публикацию [16]. Здесь также перечислим основные аргументы.

Рассматривая две взаимно удаляющиеся запутанные между собой частицы с ненулевой массой покоя, у одной из которых измеряется координата, а у другой импульс, следует иметь в виду, что сколь угодно точное измерение обеих величин при сохранении взаимной корреляции противоречило бы соотношению неопределенностей Гейзенберга в лабораторной системе отсчета. Это рассуждение было бы верно, если бы частицы можно было мыслить идеальными ^механическими шариками”. Но в реальности, как мы постараемся убедить читателя далее, квантовые частицы нельзя считать механическими шариками, между которыми не существует никакой связи.

Действительно, массивные квантовые частицы (в частности, электроны) обладают не только корпускулярными, но и волновыми свойствами. Так, для электрона Дираком в 1928 г. было получено [17] релятивистское описание волновой функции в виде системы четырех дифференциальных уравнений для четырех спинорных величин, где одна пара отвечает положительной, а

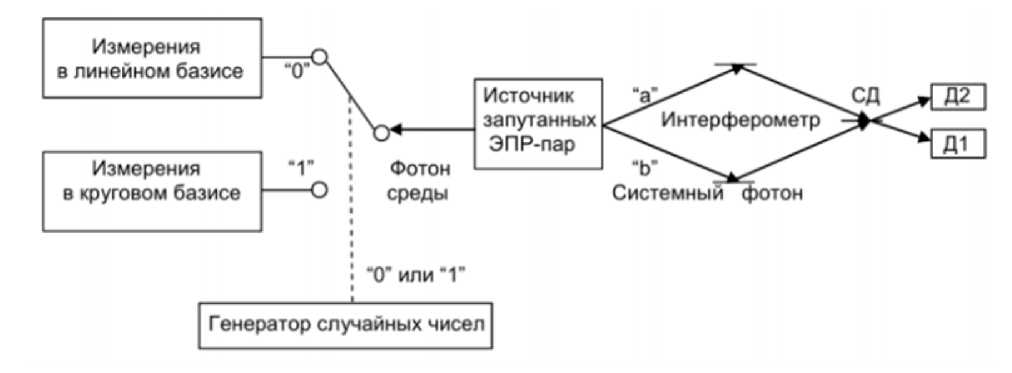
Рис. 5. Концептуальная схема экспериментов в работе [15]

вторая пара - отрицательной энергии электрона, и в каждой паре одна из величин отвечает одному направлению спина, а другая - противоположному. При этом операторы для составляющих скорости электрона не коммутируют между собой, а собственные значения каждого из них в результате измерения обязательно должны быть равны по абсолютной величине скорости света. Такой парадоксальный результат Шрёдингер в 1930 году объяснил [18] наличием у электрона двух компонент скорости - обычной (медленной) и быстро осциллирующей с частотой, отвечающей периоду волны де Бройля для электрона. Он писал там же по этому поводу: ^Квадрат каждой компоненты скорости может, следовательно, принимать только значение с², причем наряду с этим он должен в таком случае являться также средним значением (математическим ожиданием) для многих измерений на одном и том же волновом пакете. Сама компонента скорости допускает лишь значения 士 с. Ее математическое ожидание может быть и в общем будет меньшим. Тем не менее, для него ожидают порядок величины с и удивляются, как это может удаваться центру тяжести облака заряда двигаться всегда так быстро и все же при известных условиях перемещаться поступательно только с умеренной скоростью. Это, очевидно, возможно потому, что он не движется прямолинейно.^5,

Сходные представления о реальном электроне, “состоящем” из двух безмассовых компонент “zig” и “zag”, описаны в книге Пенроуза [19]: Дираковский спинор с его четырьмя комплексными компонентами можно представить в виде пары 2-спиноров <...>. Тогда уравнение Дирака можно записать в виде уравнения, связывающего эти два 2-спинора, при этом каждый из них играет в отношении другого роль «источника» с «константой связи» М/，2 (где М — масса частицы), определяющей «силу взаимодействия» между ними... Форма этих уравнений показывает, что дираковский электрон можно считать состоящим из двух ингредиентов <...>. Им можно придать некоторый физический смысл. Можно представить себе картину, в которой существуют две «частицы», <...>, причем обе они не имеют массы, и каждая из них непрерывно превращается в другую. Дадим этим частицам имена《zig» и《zag», так что одна будет описывать частицу《zig», а другая — частицу «zag». Будучи безмассовыми, они должны перемещаться со скоростью света, однако вместо этого можно считать, что они «качаются» взад-вперед, причем движение вперед частицы «zig» непрерывно превращается в движение назад частицы《zag», и наоборот. Фактически это есть реализация явления, называемого «zitterbewegung» («дрожание») и состоящего в том, что мгновенное движение электрона из-за участия в таких колебаниях всегда происходит со скоростью света, хотя полное усредненное движение электрона характеризуется скоростью, меньшей скорости света. Каждый из указанных ингредиентов имеет спин величиной Һ/2 в направлении движения, соответствующий левому вращению в случае частицы《zig» и правому для частицы 《zag». <... > Заметим, что, хотя скорость все время меняется, направление спина в системе покоя электрона остается постоянным. <... > При такой интерпретации частица《zig» выступает как источник для частицы《zag», а частица《zag» — как источник в отношении частицы《zig», сила связи между ними определяется величиной М. Рассматривая процесс в целом, мы обнаружим, что средняя частота, с которой это происходит, связана обратным соотношением с параметром связи —массой М： (фактически это есть «де-6роіі「евска，я частота» электрона.

Наконец, в работе [20] еще более ясно сформулировано, что “дрожательному” движению соответствует представление стационарного состояния электрона в виде суперпозиции двух собственных состояний оператора скорости с собственными значениями — с и -с. В итоге ^^эффeктивIIaя^^ скорость электрона равна

U z = Е - 1 卜 2 P z + i~cv_zoe^-l2Et/h /2 ) = Sz ) _m + Sz ) _osc. ⑴

Здесь Pz - проекция импульса, Е — энергия частицы, 。乞。— зиа чение 。乞 пр и 力 =0. Именно среднее значение скорости ( 。乞 )m определяется значением реалыю измеряемого импульса Pz частицы. Направления средней скорости и импульса совпадают только в стационарных состояниях с положительной энергией, тогда как в состояниях с отрицательной энергией они антипараллельны.

Таким образом, рассматривая, скажем, спины запутанных между собой электронов, мы обязательно сталкиваемся с нетривиальным волновым (колебательным) процессом, в котором взаимодействие компонент (не связанное с реально наблюдаемым движением электронов) осуществляется со скоростью света. При этом две запутанные частицы, как отмечалось выше, не могут рассматриваться в виде двух независимых механических шариков, а должны восприниматься как компоненты нелокального волнового процесса (рис. 6), простирающегося (в лабораторной системе отсчета) между его начальной и финальной точками. В то же время для удаляющегося фотона вся эта область просто стремится к стягиванию в одну точку.

• 5.    Обсуждение

  5.1.    Действие квантового ластика

5.2.    Квантовый парадокс часов

Очень интересное и весьма полное исследование схемы с квантовым ластиком было проведено в работе [21]. Прежде всего, там напоминается, что при единичном детектировании никогда не наблюдается интерференционных полос (интерференция 1-го порядка), т.е. речь идет об интерференции 2-го порядка, когда картина интерференции возникает только в результате накопления множества следов от однократного детектирования. Далее, отмечается, что необходимым условием интерференции является не столько отсутствие информации о выборе пути как таковой, сколько, строго говоря, неразличимость интерферирующих частиц. Образно говоря, если к вам пришли два неотличимых близнеца, то не так важно, по каким путям они шли. Эта неразличимость может быть частичной (например, за счет вариации угла поляризации фотонов в одном из каналов), и тогда видность интерференции плавно меняется от 0 до 1. Наконец, в ходе тонкого и подробного анализа формулируется, что стирание и возобновление интерференционной картины обусловлено уничтожением и последующим воссозданием корреляционных членов между базисными состояниями, причем в последнем случае восстановление когерентности может включать дополнительный фазовый сдвиг, т.е. не является механическим воспроизведением ранее существовавших корреляционных членов матрицы плотности.

Рис. 6. Классические и квантовые представления о паре запутанных частиц

Декларируемый нами парадокс часов в КМ имеет столь же объективный характер, сколь и в обычной области его применения - в теории относительности. Напомним, что в первые годы после обнародования считалось, что на практике его невозможно проверить, поскольку речь велась о двух инерциальных системах отсчета, связанные с которыми тела не могли бы пересечься в пространстве повторно. Однако затем решение парадокса было распространено на общую теорию относительности [22], когда улетевший с Земли путешественник поворачивает и возвращается к своему (сильнее постаревшему по сравнению с ним) брату-близнецу. Как отмечалось нами выше, сегодня этот феномен теории относительности подтвержден экспериментально.

Между тем этот феномен в квантовой области практически не осознан физиками. Первооткрыватель нарушения неравенств Белла писал о существовании квантовых корреляций, что они “V …〉 прямо-таки вопиют об объяснении, а мы не можем его дать!” [23]. Известный исследователь квантовой нелокальности Н. Жизэн недавно вопрошал читателя своей книги [24]: “Но тогда что такое пространство, если воздействия могут мгновенно соединять произвольные удаленные друг от друга области? В известном смысле принять такие воздействия как объяснение нелокальных корреляций - все равно что признать, что на самом деле они распространяются не в нашем пространстве, а следуют какому-то «черному ходу» нулевой длины вне его?'

Здесь можно провести косвенную аналогию с высказыванием авторитетнейшего российского и американского космолога И. Новикова [25]: “Простейшая модель кротовой норы <... > представляет собой два входа в трехмерном пространстве, похожих на входы в черные дыры, соединенных горловиной-мостом, лежащим вне нашего пространства-времени. Этот мост может быть очень коротким, в то время, как расстояние между входами во внешнем пространстве может быть очень большим. Таким образом, подобные кротовые норы связывают удаленные области нашей Вселенной коротким мостом.5,

Таким образом, квантовая нелокальность, парадокс ЭПР и отложенный выбор для экспериментов с фотонами в рамках нашей модели не только получают свое объяснение, но и оказываются совершенно необходимыми элементами описания реальности, вопреки скептицизму Эйнштейна и сомнениям Белла.

5.3.    Телепортация и дальнодействие

Квантовый парадокс часов позволяет найти объяснение ряду других удивительных феноменов. Одним из них является хорошо известное явление квантовой телепортации [26], когда неизвестное квантовое состояние мгновенно передается на (теоретически сколь угодно большое) произвольное расстояние. Так, в 2017 году в Китае осуществили квантовую телепортацию между космосом и Землей на расстояние более 1,2 тысячи километров. В ходе экспериментов было показано нарушение неравенств Белла (и, как следствие, принципа локальности). Эффективность передачи информации новым методом на 17 порядков превышает показатели распространенных коммерческих оптико-волоконных кабелей [], [].

Следует упомянуть также и другие феномены. Например, в широко известной статье [28] цитируется замечательная по глубине мысль Хьюго Тетроде [27]: ^Солнце не излучало бы, если бы где-либо не нашлось тела, способного поглотить это излучение … Например, если я вчера наблюдал с помощью телескопа звезду, удаленную, скажем, на 100 световых лет, то не только я знаю, что испущенный ею 100 лет назад свет достиг моего глаза, но также и звезда или ее отдельные атомы уже 100 лет назад знали, что я, который даже еще не существовал тогда, вчера вечером увижу этот свет в такое-то время.”

Но как удаленная звезда может “знать”，где и когда в будущем будет зарегистрирован испущенный ею фотон? С нашей точки зрения, это яркий пример проявления нелокальности, ха- рактерный для лабораторной системы отсчета. Авторы статьи [28], стремясь обосновать тезис Тетроде, предложили схему “мгновенного” (прямого межчастичного) взаимодействия электронов со всеми возможными будущими поглотителями испускаемого ими излучения. Эта идея, в частности, позволяет легко вывести т.н. ^радиационное затухание55 излучения, но при этом использует довольно сложные представления о комбинации опережающих и запаздывающих волн. С нашей точки зрения можно рассматривать прямое межчастичное взаимодействие (дальнодействие) как одно из проявлений эффекта нелокальности; заметим, что это можно считать подтверждением нашей гипотезы для массивных частиц. Отметим, наконец, что при нашем подходе концепция дальнодействия в физике по существу непрерывно переходит в концепцию близкодействия. В нашем случае как раз речь идет о мгновенном переносе (в предельном случае движущегося фотона, чье пройденное расстояние стремится к нулю) взаимодействия квантами электромагнитного поля -фотонами. Интересно отметить, что рассматриваемый нами эффект позволяет разрешить еще два фундаментальных парадокса квантовой механики. Первый из них связан с известной моделью Фейнмана распространения квантовой частицы из точки А в точку В “по всем возможным траекториям”. Но как может частица “мгновенно прощупать всю Вселенную55? Ответ, по нашему мнению, таков: для квантовой частицы, распространяющейся со скоростью света, ився Bceлeннaя^^ стягивается в 4-мерную точку. Второй эффект - это так называемые измерения без взаимодействия (Interaction-free measurement), когда измерение может дать информацию о том, что могло бы произойти, но не произошло (“квантовое зрение в темноте”)，при этом возникает впечатление, что информация переносится в отсутствие переноса частиц [29]. На самом деле, как мы считаем, здесь также нельзя говорить о нелокальном характере переноса информации.

5.4.    Релятивистская причинность и корреляции

Интересным представляется вопрос о сущностных различиях между причинным воздействием одного объекта на другой (с одной стороны) и корреляцией между состояниями этих объектов (с другой стороны). С формальной точки зрения, корреляцию можно рассматривать как более общий феномен, поскольку она допускает отсутствие временной задержки между эволюцией поведения двух объектов и в общем случае вероятностный характер взаимосвязи. С содержательной же точки зрения было бы предпочтительней, если бы между причинно-следственной связью (cause-effect relations) и корреляционной связью (correlations) существовал “плавный” физический переход, вопреки жесткому противопоставлению этих типов отношений, которое довольно часто декларируется со стороны некоторых физиков, отрицающих квантовую нелокальность как факт.

С нашей точки зрения, подобный плавный физический переход действительно существует [30], [31]. В самом деле, можно свести современную концепцию релятивистской причинности к утверждению о том, что передача сигнала и энергии со скоростью, большей скорости света в вакууме, невозможна. Это утверждение может быть рассмотрено на примере перемещения свободно движущейся частицы с массой покоя m из точки 1 в точку 2. Переходя к релятивистскому описанию, будем говорить о паре четырехмерных событий 1 и 2, между которыми таким образом устанавливается причинная связь, т.е. имеет место передача (в простейшем случае - однобитового) сигнала. В системе отсчета, жестко связанной с нашей частицей, релятивистски инвариантное выражение для действия S свободной частицы будет равно [10]: S12 = - /2 meds = - Л2 тс2(1т = —mc2Ti2, где ds — элемент 4-мерного интервала, dT — дифференциал собственного времени (т.е. времени в системе отсчета, в которой частица покоится), Т12 — собственное время между событиями 1 и 2. В вышеприведенном выражении в соответствии со стандартным пониманием принципа релятивистской причинности подразумевается, что действие S12 является действительной величиной, а интервал собственного времени 7І2 — времениподобный, т.е. что энергия не может распространяться со сверхсветовой скоростью. Это легко переносится и на фотон, не обладающий массой покоя. Действительно, регистрация фотона как носителя информации связана с поглощением переносимого им импульса; соответственно, и в данном случае можно говорить о переносе из одной пространственной точки в другую некоторой порции энергии.

Между тем, квантовая механика приводит к представлениям о возможности мгновенной редукции квантового вектора состояния. Очевидно, что понятие “мгновенной” редукции равнозначно утверждению о возможности сколь угодно больших скоростей (в лабораторной системе отсчета) если не взаимодействия, то, по крайней мере, некоторого взаимовлияния. Допустим возможность сверхсветового движения и посмотрим, что из этого следует. При сверхсветовом движении интервал Т в выражении для действия S = —тс2Т оказывается, как известно [10], мнимым, таким образом и действие S окажется мнимым.

Мнимые длительности, координаты и другие физические величины давно используются в работах по физике и смежным естественным дисциплинам и - особенно - в квантовой механике. Основополагающая работа В. Гейзенберга 1925 года, собственно говоря, и началась с того, что он представил координату и импульс квантовой частицы в виде бесконечного ряда комплекснозначных гармоник (см. [32]): амплитудам и энергиям переходов между состояниями он сопоставил амплитуды и частоты отдельных гармоник ряда. Таким образом, можно сказать, что Гейзенберг неявно ввел в квантовую теорию разделение процессов на два типа. Процессы первого типа соответствуют классическим аналогам, их можно непосредственно измерять (условно назовем такие процессы относительно медленными). Процессы же второго типа, которые описываются мнимыми компонентами, соответствуют чисто колебательным процессам и реализуются с очень высокими частотами, отвечающими энергиям покоя элементарных частиц (как отмечено выше, примером является ^дрожание55 дираковского электрона). Среднее значение переносимой энергии в этих колебательных процессах равно нулю. Иными словами,

• •    строго переменные во времени (колебательные) величины играют в физических теориях принципиально важную роль;

• •    для математического описания переменных во времени (колебательных) процессов не только подходящим, но и естественным инструментом является аппарат комплексных чисел;

• •    когда физический процесс является исключительно колебательным (т.е. не содержит апериодических составляющих) , передача энергии из одной точки пространства в другую принципиально отсутствует, но это в общем случае не означает, что между данными точками принципиально отсутствует любое физическое взаимодействие. Необратимой передачи энергии и информации в данном случае действительно нет, среднее значение передаваемой в любую сторону энергии равно нулю (однако среднее значение квадрата циркулирующей энергии больше нуля!), что в полной мере соответствует требованиям принципа релятивистской причинности

5.5.    Близкие подходы

Следует отметить, что некоторые исследователи пытались ввести и объяснить “мгновенное” взаимодействие, используя представления о некотором скрытом от нас этапе обычного взаимодействия. Например, в [33] была предложена так называемая транзакционная интерпретация (ТИ) квантовой механики. Согласно ТИ, при излучении и поглощении квантовой частицы, находящиеся на произвольном расстоянии источник и приемник частицы осуществляют своего рода мгновенную транзакцию (аналог банковской процедуры), в ходе которой согласуются параметры данного квантового процесса. В этой интерпретации коллапс волновой функции происходит “вне времени”, т.е. происходит сразу по всей транзакции, а не в конкретный момент, и процесс излучения/поглощения симметричен во времени. Для обоснования этой схемы привлекается идея двух волн волновых функций (прямой и обратной во времени), аналогично идее Уилера - Фейнмана для электромагнитного поля [28].

Близкая по духу концепция “скрытого” времени была предложена в работах [34] и [35]. В них предполагается, что физическое пространство - время дискретно, а ткань пространства - времени состоит из элементарных событий, то есть характерный пространственный размер «ячейки» порядка размера атома, поглотившего фотон, а временной размер - порядка времени перехода с одного уровня на другой. Физическое время в каждом конкретном эксперименте можно измерить только количеством элементарных событий, нормированном определенным образом. В теорию можно ввести сигналы из скрытых параметров, которые, - и это существенно - представляют собой часть математического аппарата теории, они не являются физическими величинами, которые можно измерить и обнаружить. Они эволюционируют в скрытом времени, которое тоже не является физическим понятием, а принадлежит лишь математическому аппарату теории.

Заключение

В результате вышеизложенного мы приходим к выводу, что парадокс часов в квантовой механике имеет гораздо более важное значение, чем это обычно признается. С ним связаны многие удивительные феномены и парадоксы квантовой механики, в том числе парадокс ЭПР, телепортация, отложенный выбор и т.п.

В парадоксе ЭПР, как мы попытались показать, очень важным является отказ от присущей лабораторной системе отсчета точки зрения о разновременности измерений Алисы и Боба. В действительности, независимо от степени их взаимной удаленности, для ЭПР-партнеров оба измерения в силу парадокса часов оказываются синхронными.

Аналогичным образом устраняется парадокс отложенного выбора. Его нужно связывать не с мгновенностью коллапса волновой функции на произвольном расстоянии, а со спецификой выбранной специальной системы отсчета, где исходное и финальные измерения всегда синхронны, как и в случае ЭПР-эксперимента.

В рамках предлагаемого подхода при телепортации исходное и финальное состояние только в лабораторной системе отсчета должны рассматриваться как удаленные; существует система отсчета, в которой эти квантовые состояния разделены нулевым расстоянием.

Наконец, предлагаемый подход позволяет увидеть плавное слияние концепции близкодействия с концепцией дальнодействия, поскольку мера взаимной удаленности оказывается относительной и в выделенной системе отсчета К?, где расстояние стремится к нулю, это взаимодействие осуществляется мгновенно. Более того, рассмотренная концепция вполне согласуется и с реляционно-статитстической парадигмой, см., напр., [36], [37], [38] и цитируемую там литературу.