Об учете формы свободной поверхности жидкости при моделировании процесса иммобилизации бактериальных клеток на твердом носителе

Сегодня наиболее разрабатываемой в биотехнологическом отношении группой актинобактерий являются представители рода Rhodococcus , осуществляющие процессы окислительной трансформации природных и антропогенных углеводородных соединений [8]. В частности, родококки синтезируют поверхностно-активные трегалозолипиды (биосурфактанты), аминокислоты, витамины, ферменты и катализируют реакции стереоселективного окисления фенилметилового сульфида (тиоанизола) и его гомологов в соответствующие ( R )- или ( S )-сульфоксиды, применяемые в химической и фармацевтической промышленности [7, 9]. Представители отдельных видов родококков ( R. ruber , R. erythropolis , R. opacus ) – активные биодеструкторы нефтяных углеводородов и других ксенобиотиков [1, 2]. Типично бактериальный, а не мицелиальный характер роста родококков, способность © Куюкина М.С., Ившина И.Б., Осипенко М.А., Няшин Ю.И., Тюленёва А.Н., Серебренникова М.К., 2009

Куюкина Мария Станиславовна, д.б.н., в.н.с. лаборатории алканотрофных микроорганизмов, Пермь Ившина Ирина Борисовна, д.б.н., чл.-корр. РАН, зав. лабораторией алканотрофных микроорганизмов, Пермь

Осипенко Михаил Анатольевич, к.ф.-м.н., доцент кафедры теоретической механики, Пермь Няшин Юрий Иванович, д.т.н., профессор, зав. кафедрой теоретической механики, Пермь Тюленёва Анастасия Николаевна, аспирант кафедры теоретической механики, Пермь Серебренникова Марина Константиновна, магистрант кафедры микробиологии и иммунологии, Пермь усваивать многие труднодоступные для других микроорганизмов органические субстраты, расти на минимальных средах и при экстремальных условиях делают использование этой группы микроорганизмов технологически перспективным [3].

В последние годы особое внимание в практике биотехнологии придается методам интенсификации микробиологических процессов путем иммобилизации клеток микроорганизмов. Для иммобилизации клеток алканотрофных родококков авторами успешно используется органический носитель на основе хвойных опилок, гидрофобизованных смесью олифы и Rhodococcus -биосурфактанта [6]. Разработана многоцелевая биокаталитическая система на основе иммобилизованных родококков, по основным технологическим параметрам (физико-химическим характеристикам, числу жизнеспособных бактериальных клеток, функциональной активности и стабильности при хранении и многократном использовании) отвечающая требованиям промышленной биотехнологии. Возможное применение разработанной биокаталитической системы заключается в получении практически ценных продуктов биосинтеза на углеводородном сырье, биоремедиации загрязненных нефтью и нефтепродуктами экосистем, производстве биологически активных интермедиатов для фармацевтической промышленности [10].

Для создания оптимальной технологической схемы и подбора эффективного режима иммобилизации бактериальных клеток необходимо построение математических моделей, адекватно описывающих данный процесс. Ранее авторами [4] построена согласующаяся с экспериментальными данными кинетическая модель процесса иммобилизации клеток родококков на твердом органическом носителе, учитывающая гидродинамические условия. Однако в построенной модели поверхность жидкой иммобилизационной среды в колбе, находящейся на движущейся платформе орбитального шейкера, условно предполагалась плоской. Фактически же поверхность жидкости не является плоской, она имеет более сложную геометрическую форму и при достаточно большой частоте движения платформы пересекается с дном колбы. В связи с этим, целью настоящей работы являлся учет формы свободной поверхности жидкости в рамках модифицированной модели процесса иммобилизации клеток родококков на твердом носителе.

Описание модели процесса иммобилизации бактериальных клеток

Экспериментальная установка и условия проведения процесса иммобилизации клеток родококков на гидрофобизованных древесных опилках описаны ранее в работе [4]. Иммобилизация осуществляется в 250-миллилитровых колбах Эрленмейера, закрепленных на платформе орбитального шейкера. Горизонтальная платформа шейкера движется поступательно таким образом, что все ее точки описывают окружности радиусом l с постоянной круговой частотой движения ω . Схематично колба может быть представлена в виде цилиндра с радиусом основания R , поскольку содержимое колбы занимает лишь небольшую часть ее объема. Высота жидкости при неподвижной платформе шейкера равна H (рис. 1).

В колбе находятся жидкость, частицы твердого носителя и клетки родококков. В начальный момент времени все бактериальные клетки находятся в свободном состоянии. С течением времени происходят процессы 1) иммобилизации свободных клеток, 2) десорбции иммобилизованных клеток с поверхности частиц носителя (с переходом их в свободные клетки) и 3) распада клеточного мицелия на короткие палочковидные формы. Последний процесс обусловлен особенностями морфогенетического цикла родококков, представленного чередованием стадий

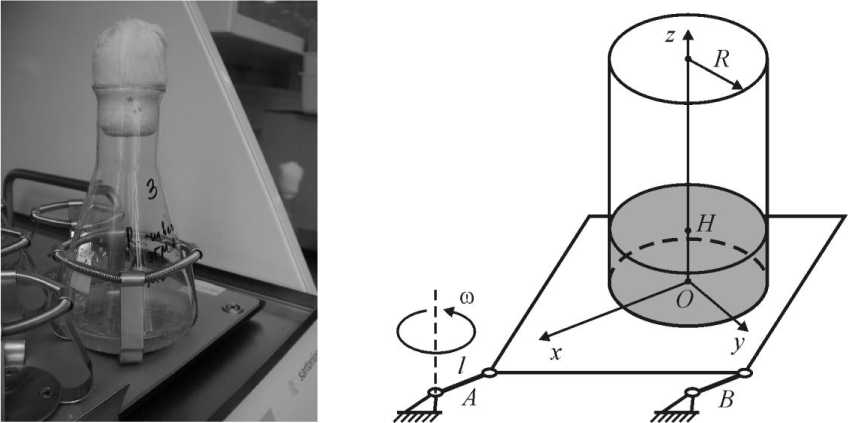
Рис. 1. Фотография и схематическое изображение основной части экспериментальной установки коротких палочковидных клеток – ветвящегося клеточного мицелия – распада клеточного мицелия вновь на короткие палочковидные формы [3].

В зависимости от значения круговой частоты to свободная поверхность жидкости в процессе перемешивания принимает различную форму. Качественно имеют место три варианта формы поверхности, описанные ниже.

Теоретическое определение формы свободной поверхности жидкости

Перейдем в подвижную (неинерциальную) систему отсчета Oxyz (рис. 1). Начало координат находится в центре основания колбы, ось х параллельна подводящим стержням A и B (см. рис. 1). В этой системе отсчета колба вращается с угловой скоростью to , а поле сил инерции является стационарным. Будем считать жидкость идеальной, тогда вращение колбы не приводит к движению жидкости. Поэтому для определения формы поверхности жидкости можно использовать уравнение гидростатики [5]

1grad P = g - a e ,                               (1)

P где p - плотность жидкости, P - давление, g - ускорение свободного падения, ae = —(to2(x — l), to2у,0) - переносное ускорение частиц жидкости. Из (1) находим

P ( x , у , z ) = p ( to ² ( x ² + у ² — 2lx ) /2 — gz ) + const.

Из (2) и условия постоянства давления на свободной поверхности жидкости получаем уравнение поверхности z (x, у, C) = — (x2 + у2 — 2lx ) + C .

Постоянная C определяется по заданному объему V = nR2 H жидкости из уравнения

JJ z ( x , у , C ) dxdy = V ,

D ( C )

где

область интегрирования D(C ) =

{ x² + у ² <  R ² }n{ z ( x , у , C ) >  0 } .

Из (3) и (4) можно установить, что существуют два критических значения ю_с1 и ю_с2 круговой частоты, имеющие следующий смысл. Если ю <  ю_сt, то свободная поверхность жидкости не пересекает дна колбы (область D – круг радиусом R , рис. 2). Если ю _c 1 < ю < ю _{c 2} , то свободная поверхность пересекает дно колбы с образованием “сухого” круга (область D – круг радиусом R , из которого исключен другой круг, см. рис. 2). Если ю > ю_{с 2}, то “сухой” участок контактирует со стенками колбы (область D - круг радиусом R , из которого исключена часть другого круга, см. рис. 2). Для ю_с1

и юс2 можно получить выражения:

2      4 gH     2         4 gH

c1   R2(1 + 2а2), c2   R2а2 (2 + (2-а)2) ’ где а = I/R < 1.

Численные значения параметров: R = 4,8 см (это значение уточнено по сравнению со значением, принятым в [4]), V = 50 см³, l = 1,25 см. Для этих значений из (5) находим ю_с1 = 97 • 2 п рад/мин, ю_с2 = 177 • 2 п рад/мин.

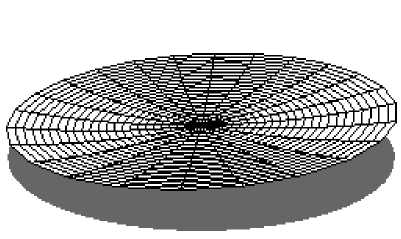
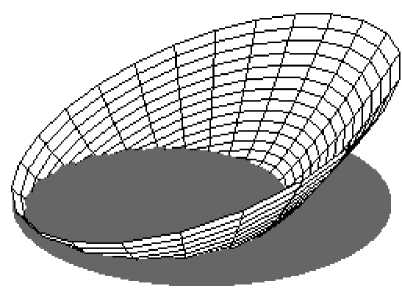
На рис. 3 показаны найденные численно из (3), (4) формы свободной поверхности жидкости при четырех различных значениях частоты движения платформы орбитального шейкера. Серым цветом показано дно колбы.

На рис. 4, а приведена экспериментальная фотография свободной поверхности жидкости для ю = 160 • 2 п рад/мин. На рис. 3, в показана теоретически найденная форма поверхности для этого значения ω. Сопоставление экспериментальной и теоретической форм проведено на рис. 4, б . Имеется удовлетворительное совпадение теории и эксперимента.

Модификация модели процесса иммобилизации с учетом формы поверхности ЖИДКОСТИ

Основным результатом ранее разработанной кинетической модели [4] является определение теоретической зависимости средней концентрации свободных бактериальных клеток от времени.

n s ( t ) = ,  т, "Zt ,  ( T < ю )/ T d ( ю ) + exp ( - ( 1 T ( ю ) + 1 T ( ю ) ) t ) ) x

¹ + т -( ^ю )/ T d ( ^ю )

x ( K ( ю ) - ( K ( ю ) - 1) exp ( - t,T f ( ю ) ) ) ,                         (6)

где n – концентрация свободных клеток в начальный момент времени,

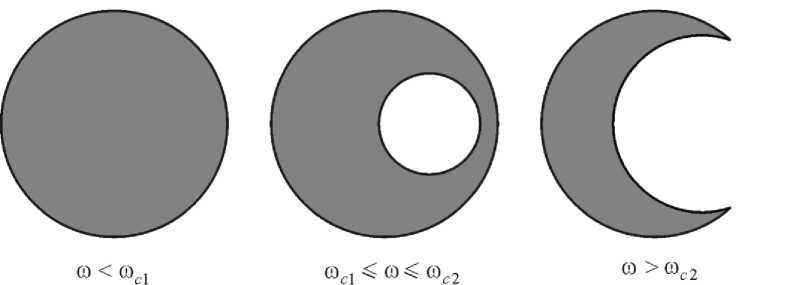
Рис. 2. Область D при различных значениях круговой частоты ω

a

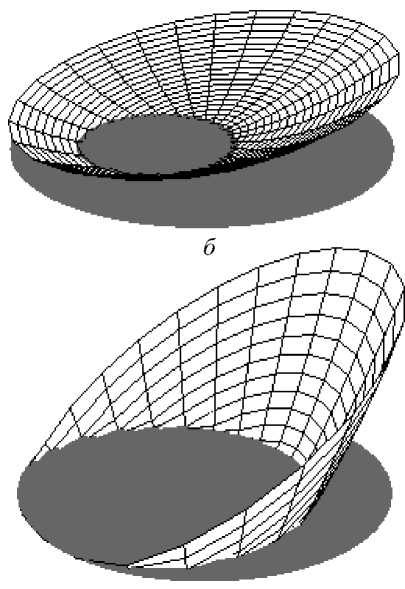
г

Рис. 3. Теоретические формы свободной поверхности жидкости при различных частотах движения платформы орбитального шейкера: ( a ) ω = 60·2π рад/мин, ( б ) ω = 110·2π рад/мин, ( в ) ω = 160·2π рад/мин, ( г ) ω = 210·2π рад/мин

в

T (го) - характерное время иммобилизации, Td (to) - характерное время, за которое клетка будет десорбирована с поверхности частицы носителя, K > 1 - кратность распада клеточного мицелия, Tf – характерное время распада. Для величины

найдено выражение

T (to) =

4 ( 1 a c ( to ) + 1 a s ( to ) ) ( 1 - exp( - a c ( to )) )( 1 - exp( - a s ( to )) ) ---------------------------------------------------------------------•----------------------------------------------------------------------------------------------------------------------

S n c to R p ( to )            1 - exp( - a c ( to ) - a s ( to ))

где

^ac ( ^to ) =

12 gV L  P i )

1 - nto2 R4 V   Pc )

as (to) =

12 gV nto ² R ⁴

V P s )

T (_Ю)

Pi - плотность жидкости, pc - плотность частицы носителя, р5 - плотность свободной бактериальной клетки, n – средняя (по объему жидкости в колбе) концентрация частиц носителя, S - площадь поверхности частицы носителя, p(to) - вероятность иммобилизации свободной клетки при ее столкновении с частицей носителя.

Сопоставляя (6) с экспериментальными данными, можно найти T ( to ) и далее из

(7), (8) теоретически найти p ( to ), что было сделано в [4]. Однако соотношение (7) справедливо только для плоской поверхности жидкости. Это соотношение было модифицировано с учетом найденной выше формы поверхности. Соответствующая модификация выглядит следующим образом:

• ⁴    ( ^{1 a}c ^{( to ) + 1 a}s ^{( to )} ) J ( ^ac ^{( to )} ) J ( ^as ^{( to )} )

  
  
  
  

T (to) = —-------------- • —7-----— ----^ ,

Sn_c to Rp ( to )        J ( a_c ( to ) + a_s ( to ) )

где

J ( a ) = — jjj exp( - az/H ) dxdyd

^VA ( to )

A ( to ) - область, занятая жидкостью в колбе.

a

б

Рис. 4. Сравнение теоретически полученной формы поверхности жидкости ( б ) с экспериментальной формой (( a ) и ( б )) при значении круговой частоты ω=160·2π рад/мин

Вероятность иммобилизации бактериальной клетки при столкновении с частицей носителя

№ п/п	ω, рад/мин	p (без учета формы поверхности жидкости)	p (c учетом формы поверхности жидкости)
1	60·2π	1,2·10-7	2,1·10-7
2	110·2π	1,9·10-8	2,8·10-8
3	160·2π	2,3·10-8	3,0·10-8
4	210·2π	5,7·10-8	6,8·10-8

С помощью модифицированных формул (9), (10) численно найдены значения вероятности иммобилизации p ( ю ) одной бактериальной клетки. При этом принимались следующие значения параметров: р l = 1,0 г/см 3 , р _c = 0,6 г/см 3 , р₅ = 1,2 г/см 3 , S = 10 мм 2 , п_с = 40 см^-3 (остальные численные значения приведены выше). Результаты расчетов приведены в таблице, где сопоставлены значения p , полученные из (7) (то есть без учета реальной формы поверхности жидкости; они несколько отличаются от результатов [4], что вызвано упомянутым выше уточнением значения R ), и значения, полученные из (9), (10) (с учетом формы поверхности).

Из таблицы видно, что учет формы поверхности жидкости в колбе приводит к увеличению значения p ; это увеличение более выражено при малых значениях ω.

Заключение

В данной работе теоретически описана форма свободной поверхности жидкой иммобилизационной среды в зависимости от значения круговой частоты движения платформы орбитального шейкера. Теоретический результат сопоставлен с экспериментальными наблюдениями, и получено удовлетворительное согласие.

С учетом формы поверхности жидкости модифицирована ранее разработанная кинетическая модель процесса иммобилизации клеток родококков на твердом носителе. Произведено уточненное теоретическое вычисление экспериментально не определяемого параметра – вероятности иммобилизации одной свободной бактериальной клетки при столкновении с частицей носителя.

Благодарности

Исследования поддержаны грантами Президента РФ для поддержки ведущих научных школ (НШ-4112.2008.4) и Программы Президиума РАН «Молекулярная и клеточная биология».