Об учете влияния температурных деформаций больших упругих элементов конструкции космического аппарата при оценке микроускорений

большие упругие элементы, космическая лабора- проекте «НИКА-Т» косинус угла между нормалью к ПСБ и направлением на Солнце должен быть выше 0,9. В таких случаях собственные движения ПСБ приводят к нарушению благоприятных условий микрогравитационно-го штиля и, как следствие, неудачному завершению ряда гравитационно-чувствительных процессов.

Если, двигаясь по орбите, КА периодически оказывается в тени Земли, то большие упругие элементы такого аппарата подвержены периодическому воздействию высоких порядка +1100 С и низких порядка ‒1700 С температур. Такие воздействия вызывают скачкообразное изменение размеров и формы больших упругих элементов КА в такой степени, что могут нарушать условия микрогравитационно-го штиля, поэтому задача оценки микроускорений, возникающих из-за температурных деформаций больших упругих элементов является актуальной и подлежит анализу. Её решение зависит от ряда факторов, таких как инерционно-массовые характеристики центрального тела КА и его больших упругих элементов, числа этих элементов, способа их крепления к корпусу и т.д.

Балочная модель упругого элемента. Для построения оценки микроускорений и доказательства актуальности поставленной проблемы в качестве модели больших упругих элементов была использована простейшая модель балки Эйлера-Бернулли. Для решения одномерной задачи теплопроводности было использовано уравнение [8]:

k^ T + B = cT

, где k – теплопроводность; В – тепловыделение в объеме; с1 – теплоемкость на единицу объема. При граничных подвижных условиях:

8 T ₂ 8 ² T

— = a —z—

8 t        8 x ²

Моделирование упругого элемента однородной ортотропной пластиной. Совсем иначе дело обстоит, если упругий элемент КА представить однородной ортотропной пластиной, уравнение теплопроводности для которой можно записать в виде [8]:

ср^- = div ( Л grad T ) + q ( x ; y ; z ; t )

d t                             v

„2   Л где a =—, л - коэффициент теплопроводно

сти, с - удельная теплоёмкость, р - плотность вещества стержня. Численное моделирование прогрева проводилось в математическом пакете Mathcad v 14 и показало, что распределение температуры по толщине стрежня выглядит так, как показано на рис. 1.

где q v ( x;y;z;t ) – локальная удельная мощность тепловыделения элемента пластины в точке А (x; y; z) . В этом случае, в отличие от балки, более корректно удаётся учесть теплоотдачу с поверхности пластины, подчиняющуюся закону Стефана-Больцмана:

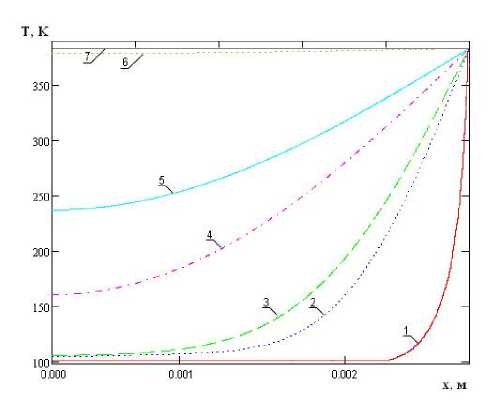
Рис. 1. Эпюра распределения температуры внутри панели радиатора: линии 1, 2, 3, 4, 5, 6 и 7 соответствуют моментам времени 0; 0,005 с; 0,01 с; 0,05 с; 0,1 с; 0,5 с и 1,6 с

—

. d T л— 8 x

x = 0 x = l

= £a I T ⁴( x ; t )|

x=0 — x = l

T c

где ε – интегральный коэффициент теплового излучения тела, σ – постоянная Стефана-Больцмана, T ⁽ x ^; t )| x = 0 - поле температур на поверхности пластины, Т с – температура окружающей среды. Считая λ , с и ρ постоянными величинами, а q v – зависящим только от времени, поскольку излучающие источники расположены на внешней поверхности пластины, можно получить оценку для микроускорений [10]:

Оценка микроускорений, полученная с помощью этой простейшей модели, даёт максимальное микроускорение [9]:

w_b = 2 • 10 - 4 м / с ²

Это значение на порядок выше допустимого уровня микроускорений для проекта «НИКА-Т» и в двадцать раз выше, чем предельный уровень для проекта «ОКА-Т». Однако связано это, прежде всего, со слишком упрощённым представлением деформации балки. Из-за температурных перепадов она удлиняется либо укорачивается, не изгибаясь, и передаёт весь дополнительный импульс корпусу КА. Поэтому вся энергия, связанная с такой деформацией, участвует в создании поля микроускорений.

w_p = 10 ⁶ м / с с

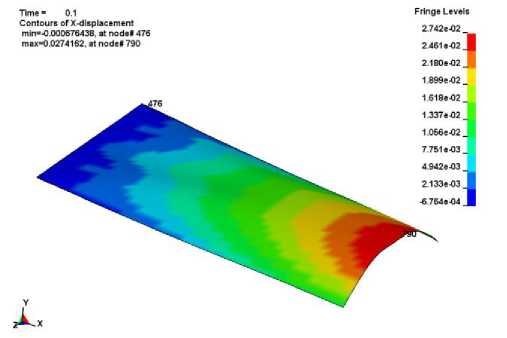
Рис. 2. Деформация пластины при её нагреве

Эта оценка в 200 раз ниже предыдущей и говорит о том, что лишь незначительная часть энергии, связанной и температурными деформациями, уйдёт в дополнительный импульс и будет участвовать в создании поля микроускорений. Большая её часть перейдёт в потенциальную энергию деформации пластины, т.е. пластина подвергается сложной деформации,

включающей растяжение-сжатие, а также изгиб. Действительно, как показало численное моделирование в математическом пакете LS-Dyna, после воздействия теплового потока со стороны Солнца она теряет прямоугольную форму (рис. 2). Прогрев пластины будет таким, как показано на рис. 3. Вся толщина пластины была разделена на 5 равных слоёв, температу-

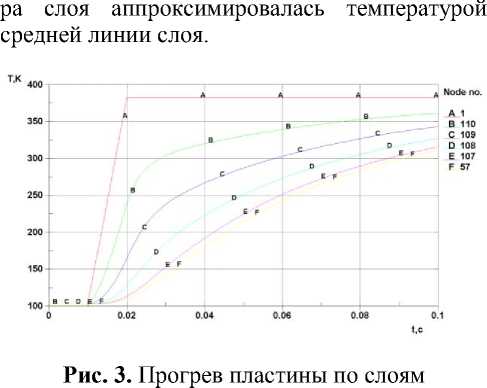
Движение элементов ПСБ при изгибе относительно недеформированного положения пластины вызовет появление момента от сил инерции. Это в свою очередь будет способствовать возникновению углового ускорения КА относительно центра масс и появлению поля микроускорений, рассматриваемых при постановки задачи в [1] при вращении КА вокруг центра масс. Для решения задачи оценки создаваемых микроускорений была построена конечноэлементная модель ПСБ с учётом характеристик материалов, используемых при её изготовлении [11]. Оценка микроускорнений была сделана исходя из анализа движения точки, принадлежащей незакреплённому краю пластины, противоположному заделке. Момент от сил инерции из-за деформации ПСБ оценивался формулой:

l

^{M ( Ф} т ) = J Y x 2 y mx ^d x 0

, где y — погонная масса ПСБ, a l - длина ПСБ. В пакете «COMSOL Multiphysics» v. 3.5a был проведён анализ движения вышеуказанной точки, а в качестве максимального ускорения рассматривалась линейная оценка ускорения движения центра масс пластины, равная половине ускорения концевой точке. В результате такого подхода оценка микроускорений составила:

W max = M^ R » 1,9 " IO — ⁵ М IС²

, где I = 16100 кг м2, а R=1 м – радиус-вектор точки размещения технологического оборудования относительно центра масс КА [1].

Таким образом, в случае пластины можно сделать вывод о пренебрежимой малости микроускорений, возникающих из-за изменения длины ПСБ, по сравнению с микроускорениями, вызываемыми моментом от сил инерции из-за изменения формы ПСБ при тепловом ударе. Также можно констатировать факт о непригодности модели ПСБ в виде балки Эйлера-Бернулли для анализа их температурных деформаций.

Нелинейная оценка. Чтобы убедиться в правильности сделанных выводов, следует построить нелинейную модель распределения линейных ускорений точек пластины. Для сравнения с полученной линейной оценкой достаточно учесть первую форму и воспользоваться упрощением [12], где первую форму предлагается оценить балочными функциями:

9 i⁽ x ) = C U ⁽ k i^x ) -

™ V ( k,x )

5 ( kJ )     i

где U, V, S – функции Крылова, k i l – i-й корень уравнения ch ( kl ) cos ( kl ) + 1= 0, а x – координата, отсчитываемая от заделки вдоль пластины.

Константа С определяется, исходя из результатов численного моделирования. Согласно [11], максимальное отклонение концевой точки составляло 16 мм при длине ПСБ, равной 5 м [1]. Тогда, ограничиваясь только первой формой, имеем:

C =

^ 1 ( l) S ( k 1 1 ) U (k 1 1 ) S ( k 1 1 ) - V ²( k 1 1 )

= 0,016 М

Используя разложение [12]:

y (x, t) = y( x )sin( pt + a) , по-прежнему рассматривая только первую форму, и пренебрегая изменением длины пластины при колебаниях (5c = x = 0), получим оценку линейных ускорений, взяв вторую полную производную по времени:

y (x, t) = - Ф1 (x )sin( pi t + a) pl где p1 – частота первого тона, которая в первом приближении может быть оценена [12]:

= 3,52 Dg_L p ¹ l ²   \ ph

, где ρ – плотность материала, h – толщина пластины, а D – цилиндрическая жёсткость на изгиб.

Соответственно оценка максимальных ускорений выглядит так:

y mx = ^ 1 ( x ) P²

.

Таким образом, вместо линейной оценки момента от сил инерции будет справедливо следующее выражение:

l

M ( Ф _т ) = Y Pi J x 2 Pi ( x ) dx

Численные расчёты проводились в математическом пакете «Mathcad» v. 14 и показали, что для тех же параметров, для которых рассчитывалась линейная оценка, значение момента от сил инерции существенно выше и составляет M ( Ф ) = 1,3 Н • м, а создаваемые максимальные микроускорения можно оценить как:

W max = ^р) R « 8,2 • IO - ⁵ M I C²

.

Выводы: собранные в работе результаты моделирования можно представить в виде сравнительной диаграммы (рис. 4).

Рис. 4. Сравнительная диаграмма оценок микроускорений, полученных с использованием разных моделей, с их допустимым значением

На рис. 4 слева направо показаны следующие значения: a – допустимое значение микроускорений для проекта технологической космической лаборатории «НИКА-Т»; b – оценка, полученная с помощью балочной модели ПСБ; c – оценка микроускорений от изменения длины пластины при тепловом ударе; d – линейная оценка микроускорений от изменения формы пластины при тепловом ударе; f – нелинейная оценка микроускорений от изменения формы пластины при тепловом ударе.

Проведенные исследования показывают, что, в отличие от задачи оценки микроускорений от работы двигателей ориентации и управления движением КА [1], модель балки Эйлера-Бернулли в качестве ПСБ не подходит даже для самой грубой оценки температурных деформаций больших упругих элементов КА, возникающих при тепловом ударе. Это связано, прежде всего, с неверным представлением о распределении энергии деформации, которая формирует дополнительный импульс при изменении длины упругого элемента, передающийся корпусу КА и создающий поле микроускорений. Этот недостаток усугубляется тем, что упругий элемент из-за его одномерного представления не излучает энергию при нагреве его Солнцем. В результате получается неадекватно завышенная оценка, пользоваться которой на практике не представляется возможным.

Моделирование ПСБ пластиной показало более сложный характер явления, чем можно было представить балочной моделью. Выявлена пренебрежимая малость микроускорений, возникающих при изменении длины пластин, по сравнению с микроускорениями, возникающими при изменении её формы. Показано, что анализ движения концевой точки пластины, лежащей на её краю, противоположному заделке, даёт существенно заниженную линейную оценку, которой нельзя пользоваться на практике. В случае возникновения спорных ситуаций следует рассмотреть более сложную нелинейную оценку линейных ускорений точек пластины, чем показано в работе, и построить более точную картину поля микроускорений.

Расчёты, выполненные для проекта космической лаборатории «НИКА-Т», свидетельствуют от актуальности учёта явления теплового удара при проверке условий выполнения микрогравитационного штиля, способствующих успешной реализации гравитационночувствительных технологических процессов. При определённых обстоятельствах тепловой удар в случае КА типа «НИКА-Т» способен нарушить эти условия, а в совокупности с другими факторами такое нарушения является ещё более вероятным. Здесь также стоит отметить, что новый проект космической лаборатории типа «ОКА-Т» предусматривает более жёсткие требования к микроускорениям, чем «НИКА-Т» [1].