Об учете возврата капитала в методе дисконтирования денежных потоков

Оценка недвижимости как инструмент измерения стоимости объекта оценки представляет собой процесс моделирования рынка этого объекта с применением разных подходов. Если при использовании сравнительного подхода создается модель рынка аналогичных объектов, то при использовании доходного подхода оценщик, по существу, моделирует действия типичного инвестора, вкладывающего свои денежные средства в приобретение или создание объекта инвестиций. Основная цель инвестиций в коммерческую недвижимость – получение дохода, который способен оправдать ожидания инвестора с точки зрения получения адекватной рынку прибыли и возврат вложенных средств (капитала) в конце инвестиционного цикла1 (см. [2, 3, 5]).

Необходимость возврата первоначального капитала к концу инвестиционного цикла вытекает из макроэкономической теории воспроизводства капитала, в соответствии с которой часть стоимости (или дохода. – С.Г. ), создаваемая в процессе производства, должна использоваться для возврата первоначального капитала как минимум в прежних объемах [6]. Этот возврат необходим для обеспечения непрерывности экономической жизни бизнеса. Заметим, что близкие по сути исследования, но в рамках макроэкономической теории экономики проводил в свое время Роберт Солоу [7]². Рассматривая модель однопродуктовой экономики (экономика Робинзона Крузо), он декомпозировал доход на потребление и на сбережение. При этом, формулируя золотое правило накопления капитала, Р. Солоу отмечал, что подушевое стационарное потребление растет при низких нормах сбережения и падает при высоких. Далее мы покажем, что нечто похожее можно обнаружить при построении модели расчета стоимости недвижимости в рамках метода дисконтирования денежных потоков.

Если объект оценки в процессе инвестиционного цикла не изменяет своей стоимости, то очевидно, что возврат первоначального капитала может быть обеспечен за счет продажи объекта в конце этого цикла. Простой пример – земельный участок, сдаваемый в аренду. Участок земли является неистощимым активом, он со временем, как правило, не теряет своей стоимости и, следовательно, не требует специальных мер по реновации.

* п ервую публикацию материалов статьи см.: н а рубеже 20-летия : сборник научно-методических статей / составители И. Л. Артеменков, В. А. Вольнова, Л. А. Лейфер, Е. И. Нейман. М. : Общероссийская общественная организация «Российское общество оценщиков», 2013. С. 236–266.

Сложнее, когда объект оценки – истощаемый актив и в процессе инвестиционного цикла изнашивается, например улучшенный земельный участок. Это значит, что выручки от продажи такого объекта после определенного времени его эксплуатации может не хватить для полного возврата первоначального капитала3. В этом случае в рамках однопродуктовой модели для возврата капитала, равного истощенной части актива, в конце инвестиционного цикла инвестор должен дополнительно использовать часть доходов от операционной деятельности4.

Анализ оценочной литературы (см., например, [2–4, 11, 15, 19]) показывает, что при оценке недвижимости с использованием доходного подхода механизм ⁵ возврата инвестиций за счет доходов в явном виде присутствует только при использовании так называемых модельных техник дохода и стоимости , в которых расчет стоимости осуществляется путем деления дохода первого года на ставку капитализации, состоящую из нормы отдачи на капитал и нормы его возврата. Норма возврата капитала в этих формулах как раз и является той составляющей, которая отвечает за возврат капитала за счет дохода. Между тем известно (см. [8, 9–12, 15]), что модельные техники оценки далеки от универсальности и корректны лишь при строго определенных допущениях в отношении тенденций изменения доходов и стоимости и в практике оценочных расчетов могут использоваться только в рамках этих допущений или при выполнении различного рода приближенных расчетов, когда допущениями можно пренебречь. При использовании же для оценки имущества универсального оценочного инструмента – метода дисконтирования денежных потоков – проблема возврата капитала за счет доходов сегодня, по нашей информации, нигде и никем не рассматривается .

В статье излагается авторский взгляд⁶ на решение этой проблемы для оценки недвижимости с использованием метода дисконтирования денежных потоков для любой динамики изменения доходов и стоимости при использовании разных методов возврата капитала. Предлагается решать эту проблему путем моделирования возврата капитала в явном виде не только за счет продажи недвижимости в конце периода владения, но и за счет периодических доходов , которые генерирует недвижимость в процессе экономической жизни.

Материал настоящей статьи посвящен оценке недвижимости. Однако основная ее идея – моделирование в явном виде использования периодических доходов для возврата капитала – после соответствующих доработок может быть распространена на оценку других видов имущества: движимости, бизнеса и нематериальных активов.

Следует отметить, что идею использования периодических доходов для возврата капитала назвать абсолютно новой нельзя, так как она, по сути, близка к идее использования амортизационных отчислений для восстановления или строительства новых основных фондов (см., например, [21]). При этом сумма амортизационных отчислений, накопленная к концу срока службы основных фондов, должна быть достаточной для полного их восстановления (приобретения или строительства). В нашем случае цель использования части периодических доходов такая же – возврат денежных средств, равных истощенной части оцениваемого актива, но способы возврата отличаются от бухгалтерских: они выполняются в соответствии с известными в оценке имущества методами возврата капитала (см. [2, 3, 5]) – методами Инвуда, Хоскольда и Ринга. При этом, так же как и в бухгалтерском учете, предусматривается, что денежные отчисления из периодических доходов в фонд возврата капитала должны быть реальными платежами, обуславливающими реальное движение денежных средств. Также предполагается, что эти денежные отчисления, направляемые на возмещение капитала, освобождаются от налога.

Заметим также, что организация и учет возврата капитала за счет операционных доходов в процессе экономической деятельности предприятия, на наш взгляд, способны уменьшить риск дефолта соответствующего проекта, так как в этом случае в процессе операционной деятельности предприятия в явном виде формируется своеобразная подушка экономической безопасности, способная минимизировать риск его банкротства.

Прежде чем изложить существо предлагаемого подхода к оценке стоимости недвижимости, рассмотрим процедуру ее оценки в рамках общепринятой, или, скажем так, традиционной модели дисконтирования денежных потоков.

Традиционная модель дисконтирования денежных потоков

Оценка недвижимости по традиционной модели дисконтирования денежных потоков выполняется с использованием следующего выражения:

V = У    I q   ₊ I k ⁺ V k

0   £ (1 + y ) q   (1 + y )k, где V0 – искомая стоимость недвижимости;

• q - порядковый номер года прогноза⁷;

• k – период прогноза (количество лет, охватываемых детальным прогнозом);

I q - чистый операционный доход q -го года⁸;

• Y – годовая ставка дисконтирования (норма отдачи на вложенный капитал);

V k - денежный поток от продажи недвижимости в конце прогнозного периода (доход от реверсии⁹).

Заметим, что нижний индекс при переменных в формуле (1), обозначающих стоимости и доходы, соответствует моменту времени, в котором зафиксирована переменная. Например, V ₀ означает, что стоимость V зафиксирована в начальный момент оси времени прогноза (см. рис. 1), который совпадает с датой оценки, а I_q означает, что доход I получен в момент времени q , соответствующий концу первого года прогноза, и так далее.

Есть в этой модели возврат капитала за счет доходов или его нет, никто не знает. Во всяком случае, из формулы (1) это не следует. Из анализа формулы мы можем сделать вывод, что в рамках такой модели оценки стоимости недвижимости возврат капитала

…

0      1      2               k– 1 k

Рис. 1. Ось времени в явном виде предусматривается только за счет одного источника - продажи недвижимости в конце прогнозного периода.

Как уже было отмечено, объект недвижимости (застроенный земельный участок) относится к истощаемым активам. Как бы собственник не поддерживал его в работоспособном состоянии в течение экономической жизни, периодически ремонтируя разные элементы конструкции, включая долговременные (фундамент, стены), объект со временем стареет как физически, так и функционально и, как следствие, уменьшается его доходный потенциал. Причем функционально он может состариться гораздо быстрее, чем физически (см., например, [20]). В связи с этим очевидно, что объект недвижимости в конце периода владения будет стоить дешевле, чем в начале этого периода. Это значит, что возврат капитала путем только продажи недвижимости в конце периода владения не решает задачу полного возврата капитала, так как остается невозмещенной стоимость изношенной части недвижимости, что делает проблематичным продолжение бизнеса, основанного на этой недвижимости. На наш взгляд, разумно компенсацию этой потери обеспечивать заранее, за счет периодического дохода, который генерирует объект недвижимости в процессе его экономической жизни. В простейшем случае эти доходы можно аккумулировать на некоторых счетах, например на депозитных счетах банков, на которых будет осуществляться наращение этих денежных средств, а затем использовать для решения задачи возврата капитала. Такие допущения, на наш взгляд, целесообразно заложить в модель оценки стоимости недвижимости методом дисконтирования денежных потоков.

В общем случае возмещение указанной потери стоимости недвижимости можно моделировать разными способами – просто откладывать часть денежных средств, которые генерирует недвижимость, в сейф или накапливать их с учетом процентов на некотором счете - фонде возврата или возмещения капитала. В теории оценки (см. [2, 3, 4, 11]) различают три способа такого возмещения: метод Ринга, метод Инвуда и метод Хоскольда.

Согласно методу Ринга (метод «сейфа», прямолинейная модель) накопления в фонде возмещения осуществляются без процентов. В связи с этим его относят к наиболее консервативным методам возврата, но считают самым безопасным (безрисковым), полагая, что сейф обанкротиться не может.

В соответствии с методом Инвуда (аннуитетная модель) накопления в фонде возмещения осуществляются с учетом процентов по ставке, равной доходности капитала инвестора или, что, как правило, то же самое, по ставке дисконтирования, которую оценщик использует для расчета текущей стоимости потока доходов и расходов. Иными словами, при использовании этого метода возврата капитала в качестве ставки процента фонда возмещения берется ставка дисконтирования. В силу того, что в методе Инвуда накопления идут по сравнительно высокой процентной ставке, его можно отнести к наиболее рисковым способам возврата капитала.

И, наконец, при возврате капитала по методу Хоскольда10 (по фонду возмещения) для наращения денежных средств используется некоторая промежуточная, «безопасная»

(в трактовке [2]) или «безрисковая» (в трактовках [3, 5]), ставка процента, большая, чем ноль, но меньшая, чем ставка дисконтирования.

Важно также, в каких ценах определять возврат капитала - в постоянных или в прогнозных. Под постоянными ценами будем понимать цены на имущество, зафиксированные на дату оценки, без учета их изменения в будущем, а под прогнозными - переменные во времени цены, которые могут сложиться в будущем как с учетом инфляции, так и с учетом изменения соотношения спроса и предложения на рынке оцениваемого имущества. При выполнении оценки в постоянных ценах для возврата первоначального капитала в конце прогнозного периода оценщику необходимо смоделировать этот возврат в денежном выражении, в точности равный величине капитала в начале этого периода. При выполнении оценки в прогнозных ценах в конце прогнозного периода оценщику необходимо смоделировать возврат капитала в объеме, достаточном для приобретения такой же с точки зрения производительности или доходности недвижимости, но в новых, как правило бо ́ льших, прогнозных ценах.

Учитывая это обстоятельство, рассмотрим предлагаемую технологию оценки стоимости недвижимости в рамках доходного подхода с использованием модели дисконтирования денежных потоков с учетом применения разных методов возврата капитала в постоянных и прогнозных ценах.

Чтобы облегчить восприятие материала, сначала рассмотрим предлагаемую технологию на в некоторой степени искусственном примере оценки полностью амортизируемого имущества, а в конце – близкий к реальному пример расчета стоимости амортизируемого имущества - объекта недвижимости, состоящего из земельного участка и его улучшений.

Дисконтирование денежных потоков с учетом возврата капитала за счет периодических доходов

Известно (см. [2]), что общий чистый операционный доход, который генерирует истощаемый (изнашиваемый) актив, условно можно разбить на две части: доход на капитал и доход для возврата капитала. Доход на капитал - это та часть общего дохода, которую может потребить сам инвестор или направить на расширение своего бизнеса. Доход для возврата капитала – это та часть общего дохода, которая необходима для того, чтобы обеспечить возврат истощенной части актива к моменту его продажи.

Учитывая это известное теоретическое положение, расчет стоимости имущества с использованием модели дисконтирования денежных потоков предлагается выполнять следующим образом:

k - 1          of

' _k - I o + V _k ^BK

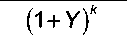
V = у ___ 0 £ (1 + Y))

где в отличие от выражения (1) I oo - доход для возврата капитала;

( I q - I^o o ) - доход на капитал;

V_k^BK - денежный поток, необходимый для возврата первоначального капитала в конце прогнозного периода.

На рисунке 2 для наглядности показаны денежные потоки, соответствующие выражению (2). На нем искомая стоимость V0 имущества в отличие от доходов и реверсии представлена как отрицательный денежный поток. Предполагается, что по этой цене может быть приобретено имущество. Иначе говоря, V0- это инвестиции в нулевой момент времени, и, следовательно, для инвестора – это отток денежных средств.

Денежный поток V_k^ВK , необходимый для возврата первоначального капитала в конце прогнозного периода, кроме выручки V_k от продажи имущества в конце прогнозного периода, содержит дополнительную составляющую - накопления A V_k в фонде возврата капитала:

V ^K =V_k +A V_k.

Накопления A V_k в фонде возврата капитала, позиционируемые вместе с продажей в конце прогнозного периода, численно равны прогнозируемому износу имущества и формируются путем реинвестирования части чистого операционного дохода в фонд возврата капитала.

V k ^ВK

I 1

I ₂

Iq

q

I k

V k

A V k

V 0

k

k+ 1    время

У

Iof

у

Iof

У

Iof

У A V k

Iof

фонд возмещения

Рис. 2. Динамика денежных потоков объекта недвижимости

Таким образом, возврат капитала в конце прогнозного периода здесь осуществляется за счет двух источников – продажа имущества и накопления в фонде возврата капитала, компенсирующие износ этого имущества . При этом при моделировании процесса оценки имущества в рамках предлагаемой модели дисконтирования денежных потоков (2) вначале дисконтируются только доходы на капитал, а потом, в конце прогнозного периода, дисконтируется денежный поток, необходимый для возврата первоначального капитала, который формируется как сумма аккумулированных отчислений в фонд возврата капитала и выручки от продажи имущества в конце прогнозного периода. Сумма дисконтированных доходов на капитал и текущей стоимости денежного потока, необходимого для возврата первоначального капитала, образует искомую стоимость оцениваемого имущества.

Иными словами, в предлагаемой модели наряду с прямым дисконтированием на дату оценки доходов на капитал имеет место отсроченное дисконтирование на эту же дату суммы аккумулированных к концу прогнозного периода доходов для возврата капитала и выручки от продажи имущества.

Износ имущества к концу прогнозного периода является следствием физического и функционального устареваний, зависит от внутренних свойств оцениваемого имущества и внешних факторов рынка [13, 20]. Будем считать, что оценщик на основе изучения априорной рыночной информации может спрогнозировать его динамику и определить выручку от продажи имущества в абсолютных или относительных показателях в конце прогнозного периода. В этом случае, вычтя из стоимости VkВK возврата капитала предполагаемую выручку Vk от продажи имущества, он сможет рассчитать сумму, которую необходимо дополнительно накопить для возврата капитала в требуемом объеме:

A V k = V_k^BK - V k .

При возврате капитала в постоянных ценах денежный поток, необходимый для его возврата, должен быть равен первоначальной стоимости V_k^ВK = V ₀. В этом случае накопления в фонде возврата капитала будут равны разности первоначальной стоимости V ₀ и выручки V_k от продажи имущества в конце прогнозного периода:

A V k = V o - V k .

Если моделировать возврат капитала в прогнозных ценах, то денежный поток, необходимый для его возврата, из-за роста цен может быть больше первоначальной стоимости этого имущества. При этом накопления, необходимые для компенсации износа имущества, будут больше разности первоначальной стоимости имущества V ₀ и выручки V_k от его продажи в конце прогнозного периода на рост цен, произошедший за этот период.

Спрогнозировав износ объекта оценки в постоянных или прогнозных ценах, можно рассчитать размер периодических отчислений из чистого дохода в фонд возврата капитала:

I o = A V k x SFF ( k , i s ) ,                                                                          (5)

где SFF ( k , i s ) =---- i s-k --функция сложного процента: фактор фонда возмещения;

(1 + is ) - 1

i s - ставка процента фонда возмещения.

Этих платежей, направляемых в фонд возврата каптала, с учетом процентных начислений по ставке процента i_s достаточно, чтобы за время k сформировать в фонде недостающую для полного возврата капитала сумму:

A V_k = I o x S ( k , i s ) ,

_x   ( 1 + i ) ^k - 1

где S ( k,i ) = i----

- функция сложного процента: фактор будущей стоимости аннуи- тета платежей.

Для расчета стоимости в выражении (2) вместо I^of подставим формулу (5):

V ₌ k -1 I q -A V k x SFF ( k , i s ) ⁰ £       (1 + Y ) q

I_k -A V x SFF ( k , i_s ) + V +A V kk  skk

(1 + Y ) ^k

Полученное таким образом выражение (7) определим как обобщенную модель дисконтирования денежных потоков , которая в зависимости от ставки i_s процента фонда возврата капитала позволяет в рамках модели дисконтирования денежных потоков смоделировать в явном виде разные способы его возврата: по методам Инвуда, Хоскольда и Ринга.

Заметим, что предлагаемая модель дисконтирования позволяет также контролировать поток доходов, направляемых как на потребление, так и на возврат первоначальных инвестиций.

Покажем, что предлагаемая обобщенная модель (7) дисконтирования денежных потоков при определенных допущениях об изменении доходов и стоимости эквивалентна известным в литературе [2–4, 9–12, 19] математически компактным моделям для расчета стоимости имущества.

Выполним такой анализ сначала для случая постоянных цен для разных вариантов изменения дохода и стоимости при различных способах возврата капитала. Характеристики таких вариантов представлены в таблице 1.

Таблица 1

Вариант	Характеристики варианта
1	Постоянные цены Постоянный доход Стоимость объекта не меняется Возврат капитала по методу Инвуда
2	Постоянные цены Постоянный доход 100-процентный износ объекта Возврат капитала по методу Инвуда
3	Постоянные цены Постоянный доход 100-процентный износ объекта Возврат капитала по методу Ринга
4	Постоянные цены Постоянный доход 100-процентный износ объекта Возврат капитала по методу Хоскольда
5	Постоянные цены Постоянный доход Частичный износ объекта Возврат капитала по методу Хоскольда

Вариант 1

Пусть в конце прогнозного периода имеет место продажа имущества по цене, равной первоначальной стоимости: V_k = V ₀. Это означает, что возврат первоначальных инвестиций мы сможем обеспечить только за счет дохода от реверсии. Дополнительных накоплений в фонде возврата здесь не потребуется. Поскольку V k = V 0 и A V k = 0, выражение (7) для расчета стоимости имущества будет выглядеть следующим образом:

к -1

V=s q=1

I q

( 1 + Y ) q

Ik + Vo k.

Допустим также, что не будет меняться и доход, который генерирует это имущество: I_q = I = const . С учетом этого допущения выражение (8) можно представить в следующем виде:

V ₀ = I x a ( * , i ) +

V 0     _,

( 1 + Y ) *

, . 1 - ( 1 + i ) " * где a ( * , i)=     i-1—

- функция сложного процента: фактор текущей стоимости ан- нуитета платежей.

Путем несложных преобразований можно показать, что полученное выражение соответствует известной модели бессрочной капитализации (см. [2, 3, 5, 8, 11]):

V ₀ = I / Y ,                                                                                                  (9)

где Y – ставка дисконтирования (ставка капитализации бесконечного равновеликого потока доходов).

Вариант 2

Предположим, что в течение прогнозного периода имущество истощилось полностью: V_k = 0. Это означает, что возврат капитала в размере первоначальной стоимости V ₀ придется обеспечивать только за счет накоплений А V * в фонде возврата капитала путем соответствующих периодических отчислений из чистого операционного дохода, каждое из которых можно рассчитать по формуле (5) с учетом того, что А V * = V ₀ Поскольку V * = 0, а А V * = V ₀, выражение (7) для расчета стоимости имущества будет выглядеть следующим образом:

V = * -1 I q - V _o x SFF ( * , i s ) ₊ I * - V _o x SFF ( * , i s ) + V _o ⁰ q : 1        ( 1 + Y ) q                   ( 1 + Y ) *

•

Пусть также i_s = Y , что соответствует возврату капитала по методу Инвуда, и I_q = I = const . Тогда, используя формулы финансовой математики, выражение (10) можно привести к следующему также известному виду (см. [2, 3, 11, 13, 19]):

Vn =------*—---?

⁰ Y + SFF ( * , Y ) ’

где Y + SFF(k,Y) = R – модель ставки капитализации, предназначенной для капитализа- ции постоянного потока доходов с нулевой реверсией в конце прогнозного срока при возврате капитала в объеме первоначальной стоимости по методу Инвуда (см., например, [11]).

Проверим тождественность¹¹ формул (10) и (11) на примере оценки истощаемого актива, который в течение трех лет генерирует постоянный поток доходов, например, в размере 100 денежных единиц (далее – д. е.), и за 3 года истощается полностью. Допустим, что норма отдачи на капитал Y = 10 процентам годовых, а ставка i_s процента фонда возмещения равна норме отдачи на капитал.

Расчет по формуле (11):

V o =

0 , 1 + 0 , 302

= 249 д. е.

Расчет по формуле (10):

V =

100 - 249 х 0 , 302 100 - 249 х 0 , 302 100 - 249 х 0 , 302    249

= 249 д. е.

( 1 + 0 , 1 )       ⁺      ( 1 + 0 , 1 ) 2        ⁺      ( 1 + 0 , 1 ) 3        ⁺( 1 + 0 , 1 ) 3

Заметим, что в процессе расчета возврат капитала в размере 249 д. е. (числитель последнего слагаемого) сформирован за счет накоплений в фонде возврата капитала по формуле (6).

Таким образом, результаты, полученные по формулам (10) и (11), совпали. Из-за произвольности исходных данных можно утверждать, что они тождественны.

Вариант 3

Предположим, что стоимость имущества в конце прогнозного периода также будет равна нулю, но возврат капитала будет происходить по методу Ринга: i_s = 0. Поскольку V_k = 0, A V k = V ₀, и с учетом предельного перехода SFF ( к , 0 % ) = 1/ к выражение (7) для расчета стоимости имущества будет выглядеть следующим образом:

к -1

V. = Х q=1

I - V o / к ( 1 + Y ) q

+ I - V o / к + V o ⁺    ( 1 + Y ) ^к

Путем математических преобразований с использованием формул финансовой математики и арифметической прогрессии выражение (12) можно свести к следующей известной формуле (см. [2, 3, 5, 19]):

V o =

I

Y + 1 к ’

где Y +1/ к = R - модель ставки капитализации, предназначенной для капитализации постоянного потока доходов с нулевой реверсией в конце прогнозного срока при условии возврата капитала в размере первоначальной стоимости по методу Ринга.

Проверим тождественность формул (12) и (13) на том же примере.

Расчет по формуле (13):

V =--- ¹⁰⁰    = 231 д. е.

⁰ 0 , 1 + 0 , 333

Расчет по формуле (12):

V o =

100 - 231х 0 , 333 100 - 231х 0 , 333 100 - 231х 0 , 333    231

= 231 д. е.

+              +               +

( 1 + 0 , 1 )                 ( 1 + 0 , 1 ) ²                 ( 1 + 0 , 1 ) 3           ( 1 + 0 , 1 ) 3

Заметим, что в процессе расчета возврат капитала в размере 231 д. е. (числитель по- следнего слагаемого) сформирован за счет накоплений в фонде возврата капитала по формуле (6), которая при возврате капитала по методу Ринга выглядит несколько проще: A Vk = Io x k.

Таким образом, результаты, полученные по формулам (12) и (13), совпали, что свидетельствует о том, что они также тождественны. Это значит, что полученная нами формула (13), предполагающая возврат капитала по методу Ринга, справедлива для оценки имущества, генерирующего денежные потоки постоянной величины.

Вариант 4

Рассмотрим наиболее общий случай – ставка процента фонда возврата капитала равна некоторой промежуточной (безрисковой) ставке, что соответствует возврату капитала по методу Хоскольда, доход, который генерирует имущество, постоянен, а стоимость реверсии равна нулю. Поскольку в этом случае V_k = 0 и A V_k= V 0 , выражение (7) для расчета стоимости имущества будет выглядеть следующим образом:

k - 1 1 - V х SFF ( k , i s ) + I - V х SFF ( k , i s ) + V £      ( 1 + Y ) q               ( 1 + Y ) k

Можно показать, что выражение (14) путем математических преобразований сводится к следующей известной формуле (см. [2, 3, 5, 19]):

I

0 Y + SFF (k ,is)’ где Y + SFF(k, is) = R - модель ставки капитализации, предназначенной для капитализации постоянного потока доходов с нулевой реверсией в конце прогнозного срока при условии возврата капитала в размере первоначальной стоимости по методу Хоскольда.

Проверим тождественность формул (14) и (15) при тех же исходных данных: Y = 10%, k = 3, I = 100 д. е. Только ставку i_s процента фонда возмещения возьмем в размере 5 процентов.

Расчет по формуле (15):

V o =

0 , 1 + 0 , 317

= 240 д. е.

Расчет по формуле (14):

V o =

100 - 240 х 0 , 317 100 - 240 х 0 , 317 100 - 240 х 0 , 317    240

= 240 д. е.

+++

( 1 + 0 , 1 )                 ( 1 + 0 , 1 ) 2                  ( 1 + 0 , 1 ) 3           ( 1 + 0 , 1 ) 3

Заметим, что здесь, так же как и ранее, возврат капитала в размере 240 д. е. в числителе последнего слагаемого сформирован за счет накоплений в фонде возврата капитала по формуле (6).

Таким образом, результаты, полученные по формулам (14) и (15), совпали, что свидетельствует о том, что и они тождественны.

Мы рассмотрели ряд примеров дисконтирования постоянных денежных потоков доходов, в которых предполагалось, что стоимость имущества в конце прогнозного периода будет равна нулю. Теперь допустим, что эта стоимость в конце прогнозного периода отлична от нуля.

Вариант 5

Запишем выражение для оценки стоимости имущества, генерирующего постоянный поток доходов, в рамках обобщенной модели (7) дисконтирования денежных потоков при условии, что стоимость в конце прогнозного периода отлична от нуля:

k -1

V -I q=1

I -A V k x SFF ( k , i s ) ( 1 + Y ) q

I -A V x SFF ( k , i, ) + V +A V

I                k                 ^x                   k            k

( 1 + Y ) ^k

Можно показать, что выражение (16) сводится к следующей известной формуле (см. [2, 3, 19]):

V o =

I

Y + 5 V k x SFF ( k , i s ) ’

где 5 V_k = A VJV 0 - относительное изменение стоимости имущества за время прогнозного периода;

Y + 5 V_k х SFF ( k , i_s ) = R - модель ставки капитализации, предназначенной для капитализации постоянного потока доходов с ненулевой реверсией в конце прогнозного срока при условии возврата капитала в размере первоначальной стоимости по методу Хоскольда.

Как и в предыдущих случаях, проверим тождественность формул (16) и (17) при следующих исходных данных: Y= 10%, k = 3, I = 100 д. е., i_s = 5%. В дополнение к этому допустим, что имущество изнашивается к концу 3-го года на 30 процентов.

Расчет по формуле (17):

V 0 =

0 , 1 + 0 , 3 x 0 , 317

= 512 д. е.

Расчет по формуле (16):

V_k = 512 х (1 — 0,3) = 358 д. е. ;

A V_k = 512 - 358 = 154 д. е. ;

V 0 =

100 - 154 x 0 , 317 100 - 154 x 0 , 317 100 - 154 x 0 , 317 358 + 154

= 512 д. е.

( 1 + 0 , 1 )       ⁺      (1 + 0 , 1 ) 2       ⁺      ( 1 + 0 , 1 ) 3       ⁺ ( 1 + 0 , 1 ) 3

Итак, результаты, полученные по формулам (16) и (17), которые соответствуют наиболее общему случаю оценки имущества, генерирующего постоянные потоки доходов, совпали, что свидетельствует о том, что эти формулы также тождественны.

Прогнозные цены. Модель Л. Лейфера

Обратимся к работе Л. Лейфера [11], в которой рассматриваются способы расчета стоимости доходных объектов с использованием конечных математических выражений в разных типовых ситуациях изменения дохода и стоимости в процессе экономической жизни объекта оценки, в том числе для случая прогнозных цен. Кстати, уважаемый нами автор называет эти выражения формулами прямой капитализации. На наш взгляд, прямая капитализация – это капитализация дохода одного периода с использованием ставки капитализации, получаемой методом рыночной выжимки, а капитализация с использованием конечных математических выражений есть не что иное, как разновидность метода капитализации по норме отдачи на капитал, получаемая путем упрощения формулы дисконтирования денежных потоков при заранее известных темпах изменения дохода и стоимости.

В упомянутой работе автор, рассматривая типовые ситуации изменения дохода и стоимости, путем анализа традиционной модели дисконтирования денежных потоков получает конечные математические выражения для ставки капитализации, позволяющие на основе дохода одного года рассчитывать рыночную стоимость. Анализ этих выражений показал, что решения, получаемые с их помощью, полностью соответствуют решениям, которые можно получить в рамках обобщенной модели (7) дисконтирования денежных потоков.

Для доказательства рассмотрим ситуацию, которая, по мнению автора работы [11], является наиболее общей и наиболее правильно отражает реальное положение дел на рынке недвижимости (в работе она называется «типовая ситуация 8»), и для нее он получает конечное аналитическое выражение для ставки капитализации ( R )¹², с помощью которой можно выполнить оценку стоимости доходного объекта:

R = ( Y - g )

( 1 + Y ) k - ( 1 -5 V )( 1 + g ) k .     ( 1 + Y ) k - ( 1 + g ) k

где Y – ставка дохода на инвестиции;

• g – темп роста арендной платы;

• k – прогнозный период;

δ V – износ объекта недвижимости.

Для этой ситуации характерно13, что в процессе эксплуатации объект изнашивается (физически и морально) и теряет свою начальную стоимость. Одновременно общие процессы на рынке приводят к росту его стоимости и одновременному увеличению доходов от его эксплуатации. Согласно этой модели по прошествии некоторого времени стоимость объекта недвижимости может возрасти, несмотря на то, что она подвержена износу. По мнению Л. Лейфера (см. [11]), и с этим трудно не согласиться, это вполне укладывается в реалии сегодняшнего дня, когда мы наблюдаем, как стареющая недвижимость растет в цене и весьма быстрыми темпами.

При выводе формулы автор работы [11] использовал следующие предположения:

• •    в течение всего прогнозного периода растет арендная плата, и, соответственно, объект приносит чистый операционный доход, ежегодно увеличивающийся с темпом, равным g ;

• •    ежегодные платежи, образованные чистым операционным доходом, поступают в конце каждого года;

• •    часть периодического дохода, представляющая возврат капитала, реинвестируется по ставке дохода на инвестиции Y ;

• •    по окончании прогнозного периода объект утрачивает часть своей первоначальной стоимости вследствие износа. Известен процент γ утраченной стоимости, то есть будущая стоимость V_k в ценах текущего года (если бы отсутствовал рост цен на недвижимость) равна V k = у ^х V 0 , где V 0 - текущая стоимость (стоимость на дату оценки);

• •    в течение всего прогнозного периода на рынке недвижимости ожидается рост цен с ежегодным темпом, равным g , поэтому к концу прогнозного периода цены на рынке недвижимости вырастут в (1 + g ) ^k раз.

Сравним на конкретном примере результаты, полученные по традиционной модели (1) дисконтирования денежных потоков с использованием формулы (18), и по обобщенной модели (7).

Выполним это сравнение для следующих исходных данных:

• •    доход первого года – 1 000 денежных единиц;

• •    Y = 10 процентов;

• •    g = 2 процента;

• •    k = 5 лет;

• •    износ – 50 процентов;

• •    ставка для возврата капитала i_s = Y .

В таблице 2 показаны результаты решения с использованием традиционной модели (1) дисконтирования денежных потоков.

Таблица 2

Статья	Номер года
	1	2	3	4	5
Чистый операционный доход	1 000	1 020	1 040	1 061	1 082
Выручка от продажи Vk					3 302
Чистый операционный доход с учетом продажи	1 000	1 020	1 040	1 061	4 384
Фактор дисконтирования	0,91	0,83	0,75	0,68	0,62
Текущая стоимость потока доходов	909,09	842,98	781,67	724,82	2 722,12
Суммарная текущая стоимость потока доходов V 0	5 981

Результат решения c использованием формулы Л. Лейфера:

R = ( 0,1 - 0,02 )

( 1 + 0,1 ) 5 - ( 1 - 0,5 )( 1 + 0,02 ) 5 ( 1 + 0,1 ) 5 - ( 1 + 0,02 ) 5

= 0,167 ( 16,7% ) ;

V = I / R = 1 000/0,167 = 5 981.

Результат решения с использованием обобщенной модели (7) представлен в таблице 3.

Из сравнения полученных решений следует, что результаты расчетов c использованием традиционной модели, формулы Л. Лейфера и обобщенной модели совпали.

Итак, мы постарались показать, что известные модели расчета стоимости можно рассматривать как частные случаи аналитического решения обобщенной модели дисконти-

Таблица 3

Статья Номер года 1 2 3 4 5 Чистый операционный доход 1 000 1 020 1 040 1 061 1 082 Итоговый чистый операционный доход на капитал за минусом отчислений в фонд возврата капитала в размере 541 д. е. 459 479 500 520 542 Накопления в фонде возврата капитала AVk 3 301,6 Выручка от продажи Vk 3 301,6 Итого возврат капитала VkВK 6 603,2 Чистый операционный доход на капитал с учетом возврата капитала 459 479 500 520 7 145 Фактор дисконтирования 0,91 0,83 0,75 0,68 0,62 Текущая стоимость потока доходов 417 396 375 355 4 436 Суммарная текущая стоимость потока доходов V0 5 981 рования денежных потоков для разных заранее известных вариантов изменения доходов и стоимости и разных способов возврата капитала.

Теперь посмотрим, в чем отличие традиционной модели дисконтирования и предлагаемой (обобщенной) модели.

Сравнительный анализ формул традиционной и обобщенной моделей дисконтирования

Заметим, что в выражении (7) величина чистого дохода I^o o = A V k ^х SFF ( k , i s ), направляемого в фонд возврата капитала, постоянная. Следовательно, можно записать, что

= k "¹    Iq __ S ( k , Y ) xA V_k x SFF ( k , i s ) + V_k + A V_k

; (1+y ) q             (1+y )k              (1+y )k "

Это выражение можно представить в следующем виде:

k "I     I v=y —q—

^{0 ;} ( i + y ) q

₊ V k     A V k x [ S ( k , Y ) x SFF ( k , i s ) - 1 ]

⁺ ( 1 + Y ) ^k               ( 1 + Y ) ^k

Можно показать, что при i_s = Y , что характерно для возврата капитала по методу Инвуда, S ( k , Y ) x sff ( k , i s ) = 1. При этом последнее слагаемое в выражении (19) превращается в ноль, и в этом случае мы приходим к выражению (1).

Как мы уже отмечали, выражение (1) соответствует оценке имущества с использованием традиционной модели дисконтирования денежных потоков. В нашем случае оно оказалось следствием обобщенной модели (7) дисконтирования денежных потоков при условии возврата капитала по методу Инвуда. Это означает, что традиционная модель (1) дисконтирования денежных потоков является, на наш взгляд, лишь частным случаем или, с математической точки зрения, вырожденным решением предлагаемой (обобщенной) модели (7) дисконтирования денежных потоков в варианте возврата капитала по методу Инвуда.

Кстати, если сравнивать результаты оценки, полученные с помощью обобщенной модели (7) при использовании разных методов возврата, то можно прийти к выводу, что стоимость, полученная при использовании возврата капитала по методу Инвуда, будет наивысшей. Объясняется это тем, что последний отрицательный член в формуле (19) при возврате капитала по методу Инвуда равен нулю, а при возврате капитала по другим методам он больше нуля и, следовательно, в силу своей отрицательности уменьшает стоимость на величину:

A V o

A V k [ S ( k , Y ) x SFF ( k , i s ) - 1 ] ( 1 + Y ) k

В предельном случае, при i_s = 0, что характерно для возврата капитала по методу Ринга, такое уменьшение приобретает максимальное значение:

A V [      — 1

A V o

^k L ^k

( 1 + Y ) k

Итак, сравнительный анализ показывает, что традиционная модель дисконтирования денежных потоков является, на наш взгляд, лишь частным случаем или, с математической точки зрения, вырожденным решением предлагаемой (обобщенной) модели дисконтирования денежных потоков в варианте возврата капитала по методу Инвуда. При этом традиционная модель дисконтирования денежных потоков в отличие от предлагаемой (обобщенной) модели индифферентна к методу возврата капитала, так как в своей формуле не содержит механизм такого возврата.

Сравнительный анализ модели Акерсона и обобщенной модели дисконтирования

Эффекты изменения стоимости вследствие применения разных методов возврата капитала исследовал в своих работах Чарльз Акерсон [15, 16]. В частности, он получил модель дисконтирования денежных потоков, которую можно представить в следующем виде:

k- 1

V o = £ q q = 1

-A V k x ( Y - i_s ) x SFF ( k , i s ) x S ( q - 1,i s )

( 1 + Y ) ^q

+ I k - A V k x ( Y - i s ) x SFF ( k , i s ) x S ( k - 1 , i s ) + V k ( 1 + Y ) ^k

Заметим, что в силу произвольности тенденции изменения потока доходов I_q = var , а также из-за очевидной связи конечной и начальной стоимостей ( A V_k = V 0 - V_k ) решить уравнение (22) можно только методом последовательных приближений.

Можно показать, что при постоянном потоке доходов I_q = I = const выражение (22) имеет уже известное нам компактное решение (17).

Из анализа выражения (22) следует, что если ставка процента is фонда возврата капитала строго меньше нормы отдачи на капитал, то имеет место уменьшение стоимости объекта оценки. Чарльз Акерсон квалифицировал такое уменьшение стоимости как потери при реинвестировании доходов в фонд возврата капитала14. Эти потери, показанные в выражении (22) в числителе суммы в виде слагаемого с отрицательным знаком, по его мнению, возникают из-за того, что дополнительный процентный доход, получаемый в фонде возврата капитала при реинвестировании по методам Хоскольда или Ринга, меньше дохода на собственный капитал, характерный при возврате капитала по методу Инвуда. Или, другими словами, при возврате капитала по методу Инвуда отчислений в фонд возврата капитала требуется меньше, чем, например, при возврате капитала по методу Ринга, что позволяет увеличить доход на капитал инвестора.

Отметим, что из сравнительного анализа выражений (16), (17) и (22) следует тождественность модели Акерсона и обобщенной модели (7) в случае постоянного потока дохода. Можно показать, что они тождественны и для любой динамики потока доходов.

Убедимся в этом на следующем числовом примере.

Допустим, что объект недвижимости генерирует неравномерный поток доходов в течение пяти лет: 1-й год – 60 д. е., 2-й год – 220 д. е., 3-й год – 150 д. е., 4-й год – 220 д. е., 5-й год – 90 д. е. В конце 5-го года объект продается за 70 процентов от своей первоначальной стоимости. Приемлемая для оцениваемого объекта рыночная норма отдачи на капитал (ставка дисконтирования) равна 12 процентам годовых. Возврат капитала планируется выполнить по безрисковой ставке в размере 5 процентов годовых. Требуется рассчитать стоимость объекта недвижимости.

Решим эту задачу двумя способами: по формуле Акерсона (22) и с использованием обобщенной модели (7). Заметим, что задача в такой постановке может быть решена только методом последовательных приближений.

Результаты решения задачи по формуле Акерсона представлены в таблице 4.

Таблица 4

Статья	Номер года
	1	2	3	4	5
Чистый операционный доход	60	220	150	220	90
Потери	0	3,2	6,5	10,0	13,7
Итоговый чистый операционный доход за вычетом потерь	60	216,8	143,5	210,0	76,3
Выручка от продажи Vk					586,7
Фактор дисконтирования	0,89	0,80	0,71	0,64	0,57
Текущая стоимость потока доходов	53,6	172,8	102,1	133,4	377,9
Суммарная текущая стоимость потока доходов V 0	838,2

Результаты решения этой же задачи с использованием обобщенной модели представлены в таблице 5.

Таблица 5

Статья	Номер года
	1	2	3	4	5
Чистый операционный доход	60	220	150	220	60
Итоговый чистый операционный доход на капитал за минусом отчислений в фонд возврата капитала в размере 45,51 д. е.	14,5	174,5	104,5	174,5	14,5
Накопления в фонде возврата капитала A V k					251,4
Выручка от продажи Vk					586,7
Итого возврат капитала VkВK					838,2
Чистый операционный доход на капитал с учетом возврата капитала	14,5	174,5	104,5	174,5	882,7
Фактор дисконтирования	0,89	0,80	0,71	0,64	0,57
Текущая стоимость потока доходов	12,9	139,1	74,4	110,9	501
Суммарная текущая стоимость потока доходов V 0	838,2

Как видно из таблиц 4 и 5, результаты решений задач, выполненных по формуле Акерсона и с использованием обобщенной модели, совпали, что свидетельствует об эквивалентности моделей.