Об угле Уилсона в нормированном пространстве

Проблема характеризации гильбертова пространства в классе банаховых пространств является довольно интересной и популярной проблемой в функциональном анализе. Известно большое количество критериев гильбертовости банаховых пространств. В этой статье мы приводим одно из условий, характеризующее гильбертово пространство в классе банаховых пространств.

В работе [1] Уилсон определил угол в произвольном метрическом пространстве X с метрикой d следующим образом: если a, b, с Е X — произвольные точки, то угол (бас) с вершиной в точке а определяется по формуле bac = arccos

d² (а, б) + d² (а, с) — d² (b, с)

2d^a, ЬДД, с)

Покажем, что это определение корректно, т. е.

— 1 < arccos

d² (а, б) + d² (а, с) — d²(b, с)

2d^a, ЬДД, с)

< 1.

Действительно, с одной стороны, d^b, с) < d^a, б) + d^a, с);

d²^b, с) <  d²^, б) + d²^a, с) + 2d(a, ЬДД, с);

—2d(a, b^a, с) <  d²^b, а) + d²^a, с^ — d²^b, с).

С другой стороны, d^b, с) > d^a,^ — d^a,c\, d2(b, с) > d2^, б) + d2^a, с) — 2d(a, ЬДД, с);

2d(a, b^a, с) >  d²^b, а) + d²^, с^ — d²^b, с).

Следовательно, (2) выполняется и определение (1) корректно.

Если R, R' — два метрических луча (метрический луч — конгруэнтный образ полупрямой) с общей начальной точкой а такие, что b Е R, с Е R' , то лучи R, R' образуют угол \R, R¹], если существует Нт^с-^ Ьас, когда б, с стремятся к а по метрическим лучам R и R' соответственно.

В работе [2] в качестве метрического пространства рассматривалось произвольное нормированное пространство над полем R вещественных чисел и был доказан следующий результат ([2; теорема 6]).

Теорема 1. Линейное нормированное пространство В является пространством со скалярным произведением тогда и толвко тогда, когда существует lim^c-^ bac при b и с стремящихся к а по лучам р и о соответственно для любой тройки точек а, Ь, с и любой пары лучей, проходящих через a, b и а, с соответственно.

Доказательство этой теоремы основывается на пяти утверждениях и теореме из [3]. Мы дадим прямое доказательство приведенного факта.

Заметим, что если a,b G X, то алгебраическая прямая, проходящая через а и Ь, определяемая следующим образом:

L(a, 6) = {ж G X : ж = Aa + (1 - А)6 : A G Щ, является метрической прямой, т. е. отображение

Aa + (1 — А)6 -+ (1 - А)||а - Ь\\

является конгруэнцией между L^a, b) и действительной прямой. Обратно, если а и b две различные точки в X, то а и b определяет единственную метрическую прямую, а именно, алгебраическую прямую.

Действительно, пусть луч берет начало в а и проходит через Ь, тогда ||ж — а|| = || Aa + (1 — А)6 — а|| = ||(1 — А)а +(1 — A)b|| = (1 — А) ||а — 6||; следовательно, отображение (3) ставит в соответствие каждой точке (-)ж G L^a,^ расстояние от начала луча до этой точки, таким образом, L^a,^ — метрическая прямая. А если a,b G X такие, что а ^ Ь, то через них можно провести только одну прямую А с началом в (-)а и А = L^a, b) = {ж = Аж + (1 — А)у, A G [0,1]} — метрическая прямая (если предположить, что можно провести две прямые через а и b (а ^ Ь), то тогда нарушается конгруэнтность отображения (3)).

Приведем доказательство теоремы.

< Пусть В — пространство со скалярным произведением. Покажем, что существует lim^c-m bac, где b и с стремятся к а по полупрямым р и о соответственно. Возьмем произвольные точки Aa + (1 — АД на луче р и ра + (1 — р^Ь на луче о. Тогда,

—               a - (1 - АД - Ха ² + a - (1 - р^с - ра ²

lim bac = arccos пт — ---— —  —л—л---—---------— ь,с^а             А,м-ы 2 a — (1 — АД — Aa • a — (1 — р)с — ра\\

|| Aa + (1 — АД — ра — (1 — /Дс||²

2||a — (1 — АД — Аа|| • ||а — (1 — р^с — ра\\

= arccos lim А,м->1

" (1 - А)²||а - 6||² + (1 - ц)²||а - с||² . 2(1 - А)(1 - ц)||а - Ь\\ • ||а - с||

((1 — А)(6 — а) + (1 — ц)(а — с);(1 — А)(6 — а) + (1 — ц)(а — с))' 2(1 - А)(1 - р)\\а - Ь\\ • ||а - с||                    _

[" (1 - А)²||а - 6||² + (1 - р)²\\а - с||² - (1 - А)²||а - 6||²

4-62

Лиана М. Энеева

2(1 — А) (1 — /z) (a — с, a — b)              (a — c,a — b)

= arccos lim —----—----—---- t— ---— = arccos  ----—— ---—.

A,M^1 2(1 - A)(l - /z) a - c • a - b\\            a - c • a - b\\

Таким образом, lim^c-^ bac не зависит от того, как точки по полупрямым рис стремятся к а. Следовательно, 1ппь|С_>о bac существует и lim bac = arccos Ь^с—Уа

||_a-6||2 ₊ ||_a-_C||2-||6-_C||2 2||a - b\\ • ||a - c||

Обратно, пусть В — линейное нормированное пространство, в котором существует lim^-^ bac, b и с стремятся к а по полупрямым ри а соответственно, имеющим общую начальную точку (•)«. Тогда предел не зависит от пути по которому b и с стремятся к а по полупрямым р и а соответственно. Действительно, lim bac = arccos lim

Ь^с—Уа

A—^ 1

||a — (1 — A)6 — Aa||2 + ||a — (1 — A)c — Aa||2 2||a — (1 — A)6 — Aa|| • ||a — (1 — A)c — Aa||

||Aa + (1 — A)6 — Aa — (1 — A)c||2

2||a — (1 — A)6 — Aa|| • ||a — (1 — A)c — Aa||

= arccos lim

A—1

(1 - A) = Un - b||= + (1 - Л)= ||a - cF - (1 - A)2!!» - e|| =

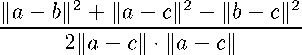
С другой стороны, lim bac = b,c—¥a

_             (1 - A)²||a - < + (1 - /z)> - c||² - ||(1 - p> " c) - (1 - A)(a - 6)||²

2(1 — A)(l —/z)||a — 6|| ■ ||a-c||                        '

Положим 1 — A = a; 1 — /z = /3. Следовательно, a, p —> 0 и пусть a, p связаны соотношением p = у. Тогда, продолжая предыдущее, получим:

lim bac = arccos lim

Ь^с—Уа

a,3^^

a2||a — 6||2 + /l2||a — c||2 — ||/3(a — c) — a(a — 6)||2 2a/3||a — 6|| • ||a — c||

= arccos lim a,/?— >0

a2||a — b||2 + ^||a — c||2 — ||^(a — c) — a(a — b)||2 a21|a — 5|| . ||a — c||

= arccos

lla - ^||2 + |||a - c||2 - |||(a - c) - a(a - 6)||2 IIй - b\\ ' IIй - cll

Из (4) и (5) получаем

arccos

2||fl - c|| • ||a - c||

IIй - ^112 + IIIй - с112 - Н(° -с) - а(а - ^)||2 = arccos----------------——-----------------;

II^й "b\\ • ||а-с||

||а - 6||² + ||а - с||² - \\Ь - с||² _ ||а - 6||² + |||а - с||² - Ц(а - с) - а(а - Ь)||² 2||_а-с||.||_а-с||       "               ||_а__Ь||.||_а__с||              ^;

11|« - 6||² + 11|« - с||² - jut - =||² = II» - »||² + |||<1 - =||² - 11^(0 -=)-(«- <:

1||_а - < - 1||_а - с||² = |||(а - с)² -(a-b^-^b- с||²:

2||^й _ _Ь||2 _ ц_а _ _Сц2 _{= 4}ц 1 _(а _ _с) _ _(а _ _Ь)||2 _ ₂ц_ь _ _С||2.

21| а — Ь||2 + 21| b — с||2 = ||а-с||2 + ||(а-с) -2(а-6)||2:

21| а — Ь||² + 21| b — с||² = ||а — с||² + || — а — с + 26||²:

2||а - 6||2 + 2||6 - с||2 = ||а - с||2 + ||(6 - с) - (а - Ь)||2.

Положим X = a — b, Y = b — с, так как а, Ь, с произвольны, следовательно, мы ничего не нарушаем; тогда последнее выражение примет вид

2||Х||2 + 21| У ||2 = ||У + У||2 + ||У - У||2,

• т. е. для любых двух элементов X и У из В выполнено тождество параллелограмма. Следовательно, В — пространство со скалярным произведением.