Об уникальности решений линейных интегральных уравнений Фредгольма первого рода на полуоси

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                       

В работе для систем линейных интегральных уравнений Фредгольма третьего рода сформулированы и доказаны теоремы об уникальности на основе метода М. М. Лаврентьева [1].

В исследовании с использованием нового подхода рассмотрены проблемы существования и уникальности решений линейных и нелинейных интегральных уравнений Фредгольма третьего рода с многоточечными особенностями [2].

Работа [3] посвящена изучению одного класса систем линейных и нелинейных интегральных уравнений Фредгольма третьего рода с применением модифицированного метода, предложенного в [4].

Анализируются вопросы уникальности решений одного класса линейных интегральных уравнений Фредгольма первого рода на прямой [5].

Рассматриваются вопросы существования и уникальности решений одного класса линейных интегральных уравнений Вольтера первого рода в пространстве дифференцируемых вектор-функций [6]. Авторы предлагают методы, направленные на доказательство уникальности решений таких систем с учетом особенностей их структуры и свойств соответствующего функционального пространства.

Исследуются системы линейных интегральных уравнений Фредгольма третьего рода, определённые на полуоси, с учетом особенностей, что расширяет область применения теории для более сложных систем и реальных задач [7].

Для начала рассмотрим уравнение следующего типа:

ю

Ku = ^ K ( t , sU ( s ) ds = f ( t ) ,   t e [ a , от )

a к к где J | K(t, s)|2dsdt < к, aa

A ( t , s ) ,   a < s <  t <к ,                                           (2)

K ( t , s ) =<

^ B ( t , s ) ,   a <  t < s <к .

Предполагается, что B ( t, s ) и A (t, s) — дважды непрерывно дифференцируемые функции на соответствующих интервалах { ( t , s ): a <  s <  t < к } , и { ( t , s ): a <  t <  s < к } , решение u ( t ) рассматривается в L ₂ [ a , к ) , где L ₂ [ a , к ) , - пространства квадратично суммируемых функций в [ a , да ) .

Допускается, что будут выполнены следующие условия:

Производные от a ) H ( t , s ) = A ( t , s ) + B ( s , t ) , ( t , s ) e G = {( t , s ), a <  s <  t < к } ;

H'(t,s), Hs(t, s), H"„(t,s)e L2(G);

• б)   lim H ( t , a ) > 0, H t ( t, a ) < 0, при t e [ a , к ), lim H ' ( t , s ) > 0, при s e [ a , к ) ,

t ^к                                            t ^к

H s_t ( t , s ) < 0 при ( t , s ) e G ;

• в )    применяется как минимум одно из дальнейших условий:

• 1)    H _t '{t , a ) < 0 V t e [ a , к ),

• 2)    lim H ' ( t , s ) > 0 V s e [ a , к ) ,

• 3)    H{t , s ) < 0 V ( t , s ) e G .

Уравнение (1), используя соотношение (2), можно записать в виде:

Г / x x к / x / x                                                                  (3)

J A ( t , s ) u ( s ) ds + J B ( t , s ) u ( s ) ds = f ( t )

at

Теперь умножим обе части равенства (3) на функцию u (t) и затем проинтегрируем полученный результат по области a <  t < к . Тогда мы получим следующее:

к t                          к кк

, s) u (s) u (t) dsdt + J J B (t, s ) u (s) u (t)dsdt = J f (t) u (t)dt aa                        ata

Из соотношения (4), применяя формулу Дирихле, обретаем

• к    t                              к sк

J J A (t, s) u (s) u (t) dsdt + J J B (t, s) u (s) u (t)dtds = J f (t) u (t)dt, aa                       aaa к tк т.е. J J [A(t, s) + B(s, t)]u (s)u (t)dsdt = J f (t)u (t) dt .Поскольку h(t, s) = A(t, s) + B(s, t) aaa

Тогда:

к tк

J J H (t, s) u (s) ds u (t)dt = J f (t) u (t) dt aaa

Определим обозначения

t z (t, s) = J u (v) d

s

Из этого следует

d_sz ( t , s ) = - u ( s ) ds , u ( s ) ds = - d_sz ( t , s ),

z ( t , s ) u ( t ) dt = d d _t ( z ² ( t, s ) )

Посредством формул (6) и (7), а также используя интегрирование по частям и применяя формулу Дирихле к левой части равенства (5), преобразуем последнее в следующий вид да

t

да

—

t t.

j j H ( t , s ) d_sz ( t , s ) u ( t ) dt = — j H ( t , s ) z ( t , s ) — j H’_s( t , s ) z ( t , s ) dsu ( t ) dt =

a да

a

a да t

a a да

= j H ( t , a ) z ( t , a ) u ( t ) dt + j j H ‘ ( t , s ) z ( t , s u ( t ) dsdt = j H ( t , a ) z ( t , a ) u ( t ) dt +

a да t

+ j j H ‘ (t, s)z (t, s) dsu (t) dt = aa

aa

a

। да                                    да да                                                 ।

- j H ( t , a ) d_tz ² ( t , a ) + j j H ‘ ( t , s ) z ( t , s ) u ( t ) dtds = - H ( t , a ) z² ( t , a )

a

as

да

—

a

да

да

да

—

1 да            ,х.1 да да                          i

H ,^{( t} , a ) z ⁽ t , adt + -[    H s ⁽ t , sdz ⁽ t , s ^{) ds} =-lim H ^{( t} , a ) ^{z ( t} , a )

2^J                        2^{J J}                            2 t ^—да

a

a

s

да

да

да

—

—

.                                       1 .                               да *                                            1

- [H ‘ ( t , a ) z ² ( t , adt +- [[ H ‘ (t , s ) z²(t , s ) —[ H "( t , s ) z ² ( t , s ) dtds = -lim H ( t , a ) z ² (t , a )

2^J   -    '   '    '       2^jl ”   '   '    's ^j                             2 t -     '   '   '   '

a

a

s

s

да                                                         да                                                да t

—     H ‘ ( t , a ) z ²( t , a ) dt + lim H ‘ ( t , s ) z ²( t , sds —       H '( t , s ) z ²( t , s ) dsdt =

2       ‘                        2 t —да       ^s                       2         st

a

a

aa

—

да                                                         да                                                 да t

= lim H ( t , a ) z²( t , a ) —     H ‘ ( t , a ) z²( t , a ) dt +   lim H ‘ ( t , s ) z ²( t , s ) ds —       H "( t , s ) z ²( t , s ) dsdt =

2 t —да                       ₂ t                      ₂ t —да                             2

да

1                         ^да

= -lim H ( t , a ) | u ( s ) ds

2 t —да           J

a

—

a

—

a

да

t

-1 2

да

да

aa

I ^да                      t                                1 ^{да                     да}

-j H ‘ ( t , a ) j u ( t ) ds dt + -lim j H ‘ ( t , s ) j u ( Z ) d Z ds

a

a

a

s

—

1 ь ‘               Г ^г             I²

1 jj «dt, s) j u m a a            L s           _

dsdt ,

где z ( t , t ) = 0 .

Следовательно, из (4) имеем да t j j H (t, s )u (s )dsu (t) dt = aa

—

2 да

[ u ( s ) ds

a

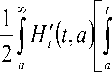
u ( t ) ds

1 2

u ( z ) d z ds

—

. b t               Г t                ²               да

^— 2 j j H ’ ⁽ t , ^s ) j ^{u ( Z )} d ^{Z dsdt} = j f ^{( t} ) u ^{( t} ) ^dt a a               | s             _                a

На основании условия, а) для любого решения u (t) уравнения (1) выводим (8).

Принимаем, что f ( t ) = 0. В этом случае, исходя из обоснованности условий б) и в), из

t

t

ОО

уравнения (8) следует, что: J u ( s ) ds = 0, или j u ( ^ ) d ^ = 0 . Сначала J u ( t)dt = 0, t е [ a , о ) затем,

a

s

t

в силу условия в) u ( t ) = 0. Таким образом, выполнено доказательство следующей теоремы:

Теорема 1. Допускается осуществление условий, а), б) и в). В этом случае решение уравнения (1) будет единственным в пространстве l₂ [ a , да ) .

Пример 1. Исследуем соотношение (1)

s при a=0,   A (t, s) = —---у при

(1 + 1 )³

t + ¹

( t , s ) е G = {( t , s ) :0 <  s <  t < да } ;      B ⁽ t , ^s ) =   ^^

при       ( t , s ) е G j = {( t , s ) : 0 <  s <  t < да } ;

( t, s ) е L ₂ (0, о). В данном случае:

H (t, s ) = A (t, s)+B (s, t ) = s       s +1

=------ 7 +------7, ( t , s ) е G

(1 + t )³    ( t + 1)²

Из (9) имеем:

1) H ‘ ( t , s ) = —

3 s     2( s + 1)

—

(1 + 1 )⁴    ( t + 1)³,

( t , s ) е G ,

1) H ‘ ( t , s ) =

(1 + 1 )^{3 +} ( t + 1)²,

( t, S ) е G ,

1) H s ( t , s ) = —

—

(1 + 1 )⁴    ( t + 1)³,

( t , s ) е G ,

Из (9) получим lim H ‘ ( t ,0 ) = 0. t ^o

Из (10) имеем H t ( t ,0 ) =

—

------y < 0 при всех t е [0, да ), ( t ⁺ 1)

Из (11) получим lim H ‘ ( t , s ) = 0 при всех s е [0, да ), t ^o

Из (12) получим H $( t , s ) = —

(   3

2    'I

--z + —т

[ (1 + 1 )⁴   ( t + 1)³ J

< 0,( t , s ) е G

Таким образом, выполняются все условия вышеуказанной теоремы, а именно условия, а), б), в). Следовательно, решение следующего интегрального уравнения

J s 3 u ( s ) ds + J ⁽ t ⁺   u ( s ) ds = f ( t ),    t е [ 0, да )    единственно в пространстве

0(1 + 1 )³              ■} ( s + 1)²

L 2 [ 0, о) .