Об уравнениях обратной задачи кинематики

Кроме изучения составных движений (т. е. движений в двух взаимно перемещающихся системах отсчёта) у кинематики как науки имеются 2 основные задачи. Если известны функция скорости v(t) определятошая движение начала отсчСта жёсткой ііеішертіііалыіоп системы s' ii матритіа собственного вращения а^ав (t) как функции собствеииого времени t, то тем самым известны и её собственные характеристики, то есть собственное ускорение W(t) и собственная угловая скорость Q(t). Эту 'за.да^т-іу опр ( ?д ( ?л ( ?ішя собственных характеристик проігзволыюп сіістемн отсчёта по известным параметрам движения v(t) и а^ав(t) назовём прямой задачей кинематики. Тогда обратная задача кинематики состоит в нахождении параметров наиболее общего преобразования в группу всех неинерциальных систем отсчёта имеющих заданное собственное ускорение и собственную угловую скорость. Из этого определения ясна важная роль данной задачи в физике. Все найденные таким образом жёсткие системы отсчёта с одинаковыми характеристиками будут обладать одинаковыми свойствами, в том смысле, что во всех таких системах отсчёта законы физики будут одинаковы, т. е. для них будет выполняться обобщённый принцип относительности А. А. Логунова [1, п. 18, с. 126, 142]. Если же собственное ускорение и собственная угловая скорость жёстких систем отсчёта равны нулю, то такие системы отсчёта являются инерциальными и обобщённый принцип относительности переходит в принцип относительности А. Эйнштейна.

Обычное решение обратной задачи кинематики в классической физике заключается в первоначальном решении уравнения для матрицы собственного вращения и подстановке полученного решения в уравнение определяющее собственное ускорение (смотри далее, соответственно, формулы (1.27) и (8.6)). В релятивистском случае такой подход к обратной задаче неправилен, поскольку он не принимает во внимание наличие собственной прецессии Томаса у неинерциальной системы отсчёта двигающейся поступательно. Между тем, собственной прецессией Томаса при релятивистских скоростях пренебречь нельзя.

• ¹    E-mail: voytikl@yandex.ru

Предлагаемые в данной статье уравнения обратной задачи кинематики и схема её решения основываются на замечательном преобразовании из лабораторной инерциальной системы отсчёта в произвольно движущуюся жёсткую неинерциальную систему отсчёта, которое в окончательном виде предложил Нэлсон [2, уравнения (9а) и (9Ь)], [3, уравнения (1),(2)] 2. Данное голономное общее преобразование автоматически учитывает факт существования собственной прецессии Томаса и фиксированность вида метрики жёсткой системы отсчёта (например [4]).

Статья построена следующим образом. В разделе 1 показано как решается прямая задача кинематики в релятивистском случае для произвольного жёсткого движения неинерциальной системы отсчёта. Далее в параграфе 2 выведены уравнения обратной задачи кинематики, а в пункте 3 предложен порядок её решения. В параграфе 4 данные уравнения проверены на непротиворечивость и самосогласованность на примере равномерно вращающегося жёсткого диска.

1.    Решение прямой задачи кинематики для жёсткой системы отсчёта

Жёсткой системой отсчёта назовём такую систему отсчёта, метрический тензор которой может зависеть от физического времени начала отсчёта t только через собствепное ускорение W начала отсчёта как функцию времени или через собственную угловую скорость Q направляющих ортов. Таким образом её 4-метрика имеет вид gik = gik(W(t),Q(t), r),                                          (i-D rje r - декартовы координаты іі(?ііп(?ртіпалыіоп системы, ^'словно (1.1) вместе с условием ненс-кривлённости пространства - времени и рядом других естественных предположений однозначно фиксирует вид метрики gik. Впервые форму метрики жёсткой ускоренной системы отсчёта открыл К. Мёллер [5, формула (17)]. Он обнаружил, что квадрат интервала в этой системе отсчёта записывается в простом виде ds2 = (1 + Wr)2dt2 - dr2                                  (1.2)

(злссъ ii палее c = 1). Какова же ( ] ) орма шітервал в том случае, ес/та система отсчёта кроме собственного ускорения ещё и вращается? Наиболее просто (но не строго) можно получить ответ на этот вопрос, если заметить, что координатные скорости в иевращающейся системе отсчёта Vn и во вращающейся системе отсчёта 7r связаны соотношением

Vn = Vr + Q X r .(1.3)

Умножая это уравнение на dt, ясно, что в (1.2) необходимо провести замену dr т dr + Q X r dt.(1.4)

Таким образом, квадрат интервала жёсткой ускоренной и вращающейся системы отсчёта должен иметь вид [6, с. 404, формула (13.71) (с поправкой на отсутствие в СТО кривизны пространства-времени)], [2]

ds2 = [ (1 + Wr)2 — (Q X r)2] dt2 — 2(Q X r)dr dt — dr2.(1-5)

Тензор кривизны Римана - Кристоффеля взятый по метрике определяемой из (7.1) действительно равен нулю, так, что предположение (1.4) оправданно.

Соотношение (7.1) собственно и является точным 4-мерным определением свойства жёсткости у неинерциальной системы отсчёта в специальной теории относительности. Необходимо только сделать замечание касающееся понимания условности термина пжёсткаяп. Дело в том, что пространственный интервал dl определяемый по метрике взятой из (7.1) имеет вид

[(Q X r)dr]2

dl2 = dr2 +  -------—  ------— ,                             (1.6)

(1 + Wr)2 — (Q X r)2 ,

• ² Во избежание недоразумений следует уточнить, что автор этого преобразования в [3] неявно считал вращение, определяемое матрицей а^ав(t) происходящим в лабораторной систсмс отсчёта. Здесь же считается, что а^ав(t) есть матрица собственного вращения.

который зависит от времени t. Отсюда видно, что так называемая жёсткая система отсчёта, при изменении собственных кинематических характеристик сохраняет расстояния только вдоль вектора угловой скорости и по радиусу от него, причём r является постоянным радиус-вектором от начала отсчёта до данной точки. Тангенциальные же расстояния (то есть расстояния по касательной к окружности вокруг вектора угловой скорости) не сохраняются. Поэтому жёсткая система отсчёта фактически является только радиально жёсткой. Абсолютное же понимание жёсткости тела, как сохранение расстояний между его любыми двумя точками, для произвольного движения в специальной теории относительности невозможно.

Переход в систему отсчёта, метрика которой имеет вид (7.1) происходит в два шага. На первом этапе осуществляется переход в систему отсчёта s заключающийся в преобразовании [2]

T

vr / t dt л/1 — v² + J 0 л/1 — v²

(1.7)

R = r +

1 — , 1 — v v²“ 一 v²

2 t

-^(vr)v + 厶

vdt

,1 — v2

(1.8)

Такое преобразование назовём специальным преобразованием Лоренца - Мёллера - Нэлсона. Оно связывает лабораторную инерциальную систему отсчёта S : (T, R) и ііеинерциалыіую систему s : (t, r). В классическом случае отрезок мс'жду любыми двумя точками ііеішертіііалыіоп жёсткой системы отсчёта, которая двигается поступательно, не изменяется и переносится параллельно самому себе. Поэтому поступательное движение полностью характеризуется всего одним вектором скорости V. В релятивистской 〉 ке (физике, вследствие сокраш.еипя Порениа ； декартовые осп системы отсчёта s относительно лабораторной системы в общем случае выглядят косоугольными и совпадают с осями такой инерциальной системы отсчёта, которая мгновенно сопутствует s. Эта. мгтювешю сопутствутоттіая іііі ( ?ртіпалыіая система отсчёта для ка.ждого момента времени своя. Вследствие этой причины, отрезок между двумя точками системы s в процессе её движения изменяется относительно лабораторной системы отсчёта. Однако, поскольку параметром преобразования (7.2), (1.8), также как и в классическом случае, является всего одна векторная величина v(t). то. для краткости, такое орбитальное двііжеіше ііеішертіііалыіоп жёсткой системы s можно продолжать называть релятивистски поступательным. При этом оказывается [4], что система отсчёта s. кроме собственного ускорения равного

,1 f2

^W = L + "^2?!—^Т^{(vv) v} ，                g)

имеет ещё и собственное вращение с угловой скоростью

Q = Qt

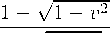
v2 1 — v2

v X v,

(1-10)

rje v = dv/dt. Данное вра ， ш,етше зашютт от характера её орбитального движения ii является собственной прецессией Томаса. Из (7.11) и (7.12) следует, что

Qt

1 — %/1 — v2 v2

v X W.

(1-11)

На втором этапе производится переход в систему отсчёта s' вращающуюся вокруг s согласно преобразованию [3]

(1-12)

Здесь и далее греческие индексы пробегают значения 1, 2, 3, а по дважды встречающимся индексам подразумевается суммирование. Также, поскольку система координат подразумевается прямоугольной, мы не будем различать ко- и контра- компоненты тензоров. Учитывая эти договорённости, для матрицы поворота аав можно записать соотношения ортогональности авааүа = аавааү = 8вү

(1-13)

и равенства «уничтожения»

е^ан%н^в a^VY = е^^вү a^aJ е^ан 〃 а^в%^ү" = е^^вү a"

(1.14)

С еавү является совершенно антисимметричным по всем шщексам единичным т(?ігзором. равным 1, если порядок индексов циклический и -1, если этот порядок антициклический. Название равенств (8.4) определяется тем, что комбинация двух матриц поворота в левой части равенства преобразуется в одну матрицу поворота в правой части (8.4). В справедливости (8.3), (8.4) нетрудно убедиться для конкретного представления матрицы поворота, например в координатах: ось поворота п. угол поворота ф аав = 8ав cos ф + nane (1 — cos ф) + еавүnY sin ф .

Соотношение обратное (8.2) есть

(1.15)

(1.16)

га _ два/в

Подставляя его в (7.2), (1.8) получим, что общее преобразование в произвольную жёсткую систему отсчёта выглядит в виде

T

vaaear‘e    / t   d， л/1 — v2 + Jо л/1 — v2

Rα

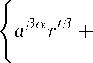
1 — %/1 — v²

V² , 1 — V²

vavY авү r'e

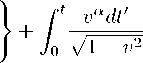
(1.17)

(1.18)

Это преобразование назовём общим преобразованием Лоренца - Мёллера - Нэлсона.

В системе s' изменение проігзвольного вектора r‘ связашюго с системой отсчёта s подчішя(?тся уравнению dr'

dt

— J 义 r'.

(1-19)

Здсч?ь з' есть вектор угловой скорости врап【етшя s' относите ль но системы s выраженный в системе координат s'. Подставляя стопа，r'a = аавre ii считая . что re = const получим. т-гто эти матритіа должна удовлетворять уравнению daαβ dt

— е^ан 〃 J3

(1.20)

Умножив (8.15) на eaAvа"/2 получим

¹ е^а 入" а ^ ^в

daαβ dt

Jv

.

(1.21)

Выберем в (9.1) конкретное представление матрицы поворота аав в какой-либо системе трёх углов ориентации. Тогда, если известен вектор з' как функция времени, то система трёх дифференциальных уравнений (9.1) фактически является задачей восстановления углов поворота по известной угловой скорости. Как впервые показал Дарбу [5, гл. 3, с. 130, п. 3.12] данная задача сводится к разысканию одного частного решения уравнения типа Риккати.

Если подставить преобразование (8.5) в интервал (7.1) (где Q = Qt ), то получится интервал такого же вида (7.1), но с новыми собственным ускорением и новой угловой скоростью равными

W'а = аав Wв ,

(1-22)

(1-23)

О'а = ааваТ + з'а .

Общая угловая скорость системы отсчёта s' складывается из собственной прецессии Томаса системы s. которая сопутствует системе s' ii вра ， ш,етш я снстемн s' относите лыю s. Подставляя в (9.2) ii

(9.3) соотношения (7.11) и (7.12) получим окончательно характеристики системы s'

产= а" 宀 ° ^в + W1? ( ^VV 酒

,

(1-24)

0^a = a^{ae 1} - "1 - ^v 2 e 耽— ^v + j^a

.

(1.25)

(1.26)

(1.27)

V2,1 — V2

В классической физике данные уравнения имеют вид

W 心= a^aeV^e,

Q'a = Ja

Второе из этих уравнений с учётом (9.1) можно решить относительно аав отдельно от первого. Очевидно, в релятивистском случае, из-за наличия собственной прецессии Томаса формула (9.5) не является независимой от (9.4).

2.    Дифференциальные уравнения для обратной задачи релятивистской кинематики

Система трёх уравнений (9.4) и трёх уравнений (9.5) относительно неизвестных трёх компонент v и трёх углов ориентации, с помошьто которых :за.да.ёт ( ?я а^ав является полной п. следователыю. допускает решение. Прежде чем его искать обратим внимание на следующее обстоятельство.

И в классическом, и в релятивистском случаях при решении задач кинематики имеется некоторое математическое неудобство, заключающееся в том, что характеристики неинерциальной системы отсчёта зависят от матрицы поворота. Это обстоятельство, хотя и является естественным, несколько затрудняет математическую запись уравнений для собственного ускорения и угловой скорости. Покажем, что используя некую подстановку можно добиться того, что уравнения для обратной задачи кинематики будут записаны в удобном векторном виде. После этого будет ясен и порядок её решения.

Введём новый вектор

V^е = a^eav^a

.

(2.1)

Физический смысл функции v'(t) заключается в том, что эта величина означает скорость начала отсчёта системы s - v(t), выраженная в системе координат s\ Из (22) следует, что v

ea /.

(2-2)

Отсюда вследствие ортогональности матрицы поворота

v

/ 2

Дифференцируя (2.3) получим, что

vV = v ' v '.

(2.3)

(2.4)

Подставим теперь (2.2), (2.3) сначала в (9.4). При этом учтём (8.3), а также (2.4). Имеем

W'“ = аав

¹   d(…)¹— v ， v ， )

[7!—"V²    dt + v ， ²(1—V ， ²) ^{( vv} 丿 a vj

a"^eV ， " + a "^ev'“

,1 — V ， ²   +

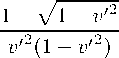
（ v ， v ， ）v ， ^a.

Затем подставим в это равенство уравнения (8.15). Тогда получим, что

W ， ^a

V ， ^a + e^aX"Jv ， "

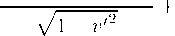
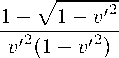
（ v ， v ， ）v ， ^a.

В векторной форме это уравнение выглядит в виде

W ，

v ， + з, X v ，

,1 — V ， ²  +

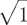
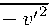
1—

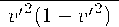
（ v ， v ， ） v ， .

(2.5)

Аналогично, в уравнении (9.5) получим в результате тех же подстановок следующую цепочку вычислений

Q'a

aae 1 ^- "1 ^- v v²“ 一 v²

■ ee"v v"Vv + з'а = aae

v ， ² v4-V 2

e^e“^vaⁿ“/ⁿ ddt 画〃 v ， x ) +

+з'а = аав

e^e " ^vaⁿ " v ' ⁿ (a^AvV 小 -е^АӨт з 田心 " v '， + J^a

( e"^e"a^aeaⁿ" ) v 也( a^AvV 小 -е^АӨтз'^Өa^TVv'^A ) + з'^а

.

В первой скобке используем равенство (8.4). Получим

1 - */l — 7)'2

Q ' ^a = — V       e^eana^evv ' ⁿ (a^AvV '入 -е^ЛӨтз ' ^өa^TVv '， + з ' ^а

V ' ²

1 - ， 1 - v'²

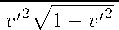
[eean(aevaAv)v'nv'A - eeanv'nеАӨтз'ө (aevaTV)v'A] + з'а

1 - ， 1 - v'² v'2 「 v2

[e^eanv 也 v ' ^e - e^eanv 也 е^АӨвз ' ^өv ' ^A] + з ' ^а

¹ — " — * e^anev'ⁿ ( v'^в + е^вӨАз'^өv'^A ) + з'^а v'² v4- 萨      '           丿

или в векторной форме

1 _- /1 _- v'² ,      ,      ,     ,       ,

Q ' =---- v ' X ( V ' + J X v ') + J.

v'2 V1 - v'2

(2-6)

Уравнение (2.6) несложно решить относительно J. Получим з' = ,1 - v'2 Q' + 1 -'；-日(Q'v')v' - 1 — '1— v'2 v' X V'.(2.7)

v'2                                        v'2' ■

Подставим теперь (2.7) в (2.5). Это приводит к следующей формуле

W' = v' + (v'v')v' + Q' X v'.(2.8)

1 一 v'²

Умножая это уравнение на v' получим отсюда, что

v ' v ' = (1 - v'²) W ' v '.

(2.9)

Произведём сейчас обратную подстановку (2.9) в (2.8). Получим в итоге простое по виду уравнение

v '= 牙 = W ' - ( W ' v ') v ' - Q ' X v '.

⑵ 10)

Данное уравнение является векторным уравнением Риккати для неизвестного вектора v'. Подставив в (2.7) уравнение (2.10) получим второе искомое уравнение

^з'=* i-^vpz v ' ^x W '.

(2.11)

Фактически данное уравнение является релятивистским уточнением правой части уравнения (9.1). Таким образом мы видим, что в формулах (2.10), (2.11) для собственных характеристик неинерциальной системы отсчёта нет матрицы поворота, так, что их возможно записать в векторном виде. Это значительно упрощает формулы.

Уравнение (8.1) вследствие своей векториости в системе s' имеет такую же форму. Надо лишь над всеми величинами поставить штрихи. Поэтому, в случае, когда Q = Qt правая часть равенства (2.11) обращается в нуль и, следовательно, а^ав = const. Поэтому выбирая новую систему координат можно добиться, чтобы а^ав = 8^ав. Так и должно быть, поскольку при движении неинерциальной системы отсчёта с собственной частотой равной частоте прецессии Томаса её собственные угловые координаты не изменяются.

Если в классических уравнениях (8.6), (1.27) аналогично провести подстановку (2.2), то можно получить похожие на (2.10) и (2.11) уравнения d V'

v' = dv_ = W' - Q' X v',

(2.12)

(2.13)

J = q'.

Сравнение релятивистских уравнений (2.10), (2.11) с классическими (2.12), (2.13) приводит к следующим очевидным заключениям. Во-первых (2.10), (2.11) отличаются от (2.12), (2.13) вторыми членами в правой части. Данные члены являются релятивистскими поправками исчезающими при c т а . В этом можно убе, 甲［工 ъся восстанавливая в (2.10). (2.11) с учётом ра<ш ( ?рпости скорость света. Кроме этого (2.12), (2.13) являются независимыми друг от друга уравнениями в отличие от (2.10) и (2.11). В релятивистском случае решение уравнения для матрицы вращения (2.11) зависит от решения (2.10).

3.    Схема решения обратной задачи кинематики

Таким образом, порядок решения обратной задачи кинематики выглядит в следующем виде. Сначала необходимо найти решение v'(t) нелинейного векторного дифференциального уравнения (2.10) первого порядка. Подстановка этого решения в (2.11) приводит это уравнение к задаче нахождения трёх углов поворота по известной угловой скорости аав (t). Знание этих углов тем самым даёт матрицу собственного вращения . Наконец подстановка уже известных величин в (2.2) определяет параметр v(t) как функцию собственного времени и шести постоянных, включающих в себя три постоянных, определяющих начальную скорость и трое начальных углов ориентации. С учётом трёх начальных координат и начального момента времени общее число начальных постоянных определяющих закон движения системы отсчёта s' с заданными характеристиками равняется десяти, как это и должно быть. Функцию скорости начала отсчёта s' v(t) можно представить в обычном виде - через лабораторное время T , находя из уравнения (7.2), где сделана подстановка r = 0 с учётом (2.3)

t

/ 7

dt

,         =T

1 - v'2(t)

(3.1)

время t как ( } ) уііктціто T ii подставляя её в v'(t) ii а^ав (t).

4.    Проверка уравнений на примере равномерно вращающегося диска

Для первичной проверки вышеизложенных уравнений рассмотрим в качестве примера систему отсчёта, начало которой находится на крае равномерно вращающегося жёсткого диска, а оси связаны с материалом из которого он изготовлен. Такая система отсчёта является ускоренной и вращающейся, причём постоянная угловая скорость её вращения перпендикулярна её постоянному собственному ускорению W'Q' = 0. Нас будут интересовать собственные характеристики такой системы отсчёта. Легко убедиться, что в этом случае величина

' v

W' X Q'

Q'2

const

(4.1)

будет являться решением первого уравнения обратной задачи кинематики (2.10). Отсюда

v

'2

W'2

О72 ■

Заметим, что при подстановке (4.1) в v‘ х W' значение этого выражения будет

/ 2

(4-3)

(4.4)

"х W' = —- С = V’2С. 0'2

Тогда подставляя (4.3) во второе уравнение (2.11) получим, что

J = ， 1 — V’² Q‘ = соnst.

Хотя решение (4.1) уравнения (2.10) и является всего лишь частным, но оно имеет непосредственное отношение к правильной зависимости скорости v(t) начала отсчёта в лабораторной системе от времени в (2.2). Действительно, в этом случае матрица ава будет зависеть от одного угла поворота 3(t)- Поэтому проектцш скорости v(t) на лабораторные координатные осп лежашпе в плоскости вращения будут периодически изменяться по законам синуса и косинуса, как это и должно быть. Угол поворота “(T) вектора скорост и начала отсчёта v(t) находится интегрированием (4.4) и учётом эйнштейновского замедления времени начала отсчёта. Получим

认 t ) = у vi

—V’² 0’dt = ， Т—

V’² 0’t + ^ 0

， 1 — V‘² 0' • ， 1 — V‘² T + 也 0 = (1 - V’²) 0’ T + 也 0 .

(4.5)

С другой стороны этот угол поворота в лабораторной системе равен

也(T )=0 T + 也 0 , rje 0 есть угловая скорость врап【етшя диска. Сравнивая вто соотношетше с (丄5) очевидно, что

0’

Т—^2.

Также используя (4.2) и (2.3) ясно, что

W ’ = v0'

v 0

1 — V2

(4.6)

(4.7)

Соотношения (4.6) и (4.7) давно известны (например [6], [4, формулы (30), (31)]).

Заключение

Знание собственного ускорения и угловой скорости как функции собственного времени полностью определяет весь класс физически эквивалентных систем отсчёта. Эта задача решается с помощью уравнений обратной задачи кинематики. Данные уравнения были представлены и проверены соответственно во втором и четвёртом разделах этой статьи. Они представляют собой простое по виду нелинейное векторное дифференциальное уравнение первого порядка типа Риккати (2.10) и давно известную систему трёх уравнений первого порядка (9.1) задачи типа Дарбу, где¹ з’ равняется (2.11). Как известно [-5. гл. 3. с. 130. п. 3.12]. систему (9.1) можно свес 工口 к поиску одного частного решения уравнения Риккати, следовательно возможно существует некая аналогия между пространством v' и пространством поворотов.

Уравнения (2.10) и (2.11) были выведены из уравнений для прямой задачи кинематики (9.4), (9.5), которые в свою очередь существенно основываются на преобразовании Лоренца - Мёллера -Нэлсона. Это обстоятельство можно рассматривать как недостаток. Поэтому в следующей статье будет показан другой способ вывода уравнений (9.4), (9.5), без необходимости ссылаться на это преобразование.

Другое направление исследований заключается в независимой последующей проверке представленного способа решения обратной задачи кинематики. Такая проверка возможна в случае, когда характеристики системы отсчёта таковы, что данные уравнения решаются. Наиболее простым и интересным является случай постоянного ускорения, который будет рассматриваться в другой статье. В общем случае, решение данных дифференциальных уравнений, имеет сложный аналитический вид, если вообще имеется. Однако с развитием компьютерных методов и технологий даже численное решение обратной задачи кинематики несомненно представляет физический интерес.

Автор выражает большую признательность профессору Н. Г. Мигранову за полезные обсуждения и поддержку.