Об устойчивости одного класса нелинейных неавтономных разностных систем

В настоящей работе рассматриваются существенно нелинейные разностные системы треугольного вида, находящиеся под воздействем нестационарных возмущений. С помощью дискретного аналога метода функций Ляпунова доказывается теорема об асимптотической устойчивости по нелинейному треугольному приближению. Показывается, что для некоторых классов систем полученные условия, при которых возмущения не нарушают устойчивости нулевого решения, можно ослабить.

Постановка задачи. Пусть задана система разностных уравнений х^к + 1) = х(к) + f (х(к)), (1) где х(к) = (хДй), ..., хп(к)) , компоненты вектора f(2) являются непрерывно дифференцируемыми при всех 2 е Еп однородными функциями порядка р > 1. Из однородности f(2) следует, что система (1) имеет нулевое решение.

Предположим, что нулевое решение однородной системы дифференциальных уравнений 2 = f (2) асимптотически устойчиво. Тогда нулевое решение системы (1) тоже асимптотически устойчиво [2].

Наряду с системой (1), рассмотрим возмущенную систему

х(к + 1) = х(к) + f (х(к)) + г(к, х(й)). (2) Будем считать, что векторная функция

r(к,z) при к = 0,1, ... непрерывна в области ||z|| <  Н, причем для любого к в указанной области справедлива оценка ^ r ( k , z)|| <  L\ |z| |^а . Здесь Н, L, а — положительные постоянные.

В соответствии с известным критерием устойчивости по нелинейному приближению [2] получаем, что при выполнении неравенства а > р нулевое решение системы (2) также асимптотически устойчиво.

Предположим теперь, что в правой части уравнений нелинейного приближения, кроме однородных членов порядка р, присутствуют слагаемые меньшего порядка, т.е. вместо системы (1) рассмотрим систему

х(к + 1) = х(к) + f (х(к)) + q(x(к)). (3) Здесь векторная функция q(z) непрерывна при |z| <  Н и удовлетворяет неравенству ||g ( z)|| <  M||z| |^Z , М > 0, 0 < X < р . Считаем, что нулевое решение изучаемой системы асимптотически устойчиво.

Рассмотрим возмущенную систему следующего вида:

x(k + 1) = x(k) + f (x(k) + q(x(k)) +

+ r(k, x(k)),              ⁽⁴⁾

где r(k,z) обладает теми же свойствами, что и возмущение в системе (2). Будем искать условия на параметр а, при которых система (4) сохраняет асимптотически устойчивое нулевое решение. В работе [3] такая задача исследовалась для систем дифференциальных уравнений. Показано, что из превосходства порядка возмущения над порядками однородности функций, входящих в правую часть невозмущенных уравнений, вообще говоря, не следует асимптотическая устойчивость нулевого решения возмущенной системы. Аналогично непрерывному случаю можно показать, что выполнение условия а > р также недостаточно для того, чтобы возмущения не нарушали асимптотической устойчивости нулевого решения системы (4).

В данной работе будем считать, что система разностных уравнений (3) является треугольной [5]. Найдем условия асимптотической устойчивости нулевого решения для возмущенных систем, а также рассмотрим классы систем, для которых возможно уточнение этих условий.

Устойчивость по нелинейному треугольному приближению. Рассмотрим систему разностных уравнений

Х 1 (к + 1) = хДк) + ^(х^к)) + q(x(к)),   (5)

х2(к + 1) = х2(к) + f2(x2(k)), где х1(к) е Е"1, x2(k) е е"2, п1 + п2 = п, х(к) = (х1*(к), х2*(к))*, элементы векторов f\(z1) и f2(z2) — непрерывно дифференцируемые однородные функции порядка р > 1, z1 е Е"1, z2 е Е"2, z = (z^, z2S, векторная функция q(z) непрерывна в области ||z|| < Н и удовлетворяет неравенству ||q(z)|| < < М z^|аz2^ , М >0, а > 0, Р>0, а + р < р. Система (5) относится к классу так называемых треугольных систем [5].

Будем считать, что нулевые решения однородных систем дифференциальных уравнений zs = fs(zs), s = 1, 2           (6)

асимптотически устойчивы. Известно [2], что в этом случае нулевое решение системы (5) также асимптотически устойчиво.

Рассмотрим теперь возмущенную систему xi(k + 1) = xi(k) + f1(xi(k)) + q(x(k)) + + r1(k, x(k)),                 (?)

х 2 (к + 1) = х 2 (к) + f 2 (x 2 (к)) + ^(к, х(к)).

Здесь векторные функции /(к, z) и / 2 (к, z) при к = 0, 1, ... непрерывны в области || z| <  Ни удовлетворяют условиям

||Е^{( k ,} z ⁾|| <  L ||z| |^а ,                 (8)

s >  1, L_s >  0, s = 1, 2. Тогда имеет место следующая теорема.

Теорема 1. Если выполнено неравенство а >р ( р -а )/ Р ,          (9)

то нулевое решение системы (7) асимптотически устойчиво.

Доказательство. Для системы (7) функцию Ляпунова строим в виде V(z) = V^z^) + + V2(z2), где V1(z1) и V2(z-) — положительно определенные непрерывно дифференцируемые однородные порядка 71 -р + 1 и у2 - р + 1 соответственно функции Ляпунова, у) и 72 —любые рациональные числа, большие ц, с четными числителями и нечетными знаменателями, причем fs (zs) ^—^ (zs) — от-azs рицательно определенные функции, s = 1, 2 [4].

Найдется Й >  0 такое, что при к >  О, ||х(к)|| <  Н получаем:

АУ <  -b_Y ( p₁(^)|р + |р₂(^)| |⁷² ) +

+ b₂ ( р₁(й)| р ^ц+ “ |р₂ (^)| |^Р + (|р₁(^)| |“ || ^ ₂ (^)| |^Р ) ^{71 Ц+1} + (|р₁(^)| |^Г + |р₂(^)| Р (|р₁(^)|р ^ц + (||т₁(^)| |“ |р₂(^)||Р^{7 1 ц} ) +

+ Р1 <^)| |°⁽⁷ 1 - ^Ц+1) + ^2 (Р| ^-^ +

+ |р₁(^)||^Г |р₂(^)||^{7 2 Ц} + р₂(^)| р ^Ц+Г +

+ |р1(^)|Г(У2 -Ц+1) + |т2а)|р72 -ц+1)) = W^)), где Ьр Ь2 — положительные постоянные.

Для существования окрестности положения z = 0,в которой W(z) будет отрицательно определенной, достаточно [4], чтобы имели место соотношения:

Y ₁ / Y ₂ >  ( р-а ) / Р ,    Y ₁ / Y ₂ <® / Р - (10)

Множество допустимых значений параметров y i , 7 2 не является пустым, если выполнено условие (9).

Выберем 71, 72 удовлетворяющие неравенствам (10). Тогда для достаточно малых значений |р(к)|| и при всех к > 0 будет справедлива оценка

АУ < -а1(|р1(^)|р + |р2(^)||72), где ^1 — положительная постоянная. Таким образом, для функции y(z) выполнены требования дискретного аналога теоремы Ляпунова об асимптотической устойчивости [2]. Теорема доказана.

Уточнение условий устойчивости по нелинейному приближению. Предположим теперь, что возмущения в системе (7) предста вимы в виде Г1(к,z) = B1(k)g1(z2), г2(к,z) =

= B 2 (k)g 2 (z 1 ), где матрицы В^к), В 2 (к)

ограничены при к >  0, компоненты векторов gpz 2 ), g2p) являются непрерывно дифференцируемыми однородными функциями порядка г > 1.

Пусть к-1

Q(0) = 0, С_г-(к) = X B/s) s = 0

при к = 1,2,..., г = 1,2.

Будем считать, что матрицы фк) ограничены при к > 0, г = 1,2. Тогда полученное в предыдущем разделе условие (9) на порядок возмущений можно ослабить с помощью предложенного в [1] способа построения неавтономных функций Ляпунова для существенно нелинейных систем.

Теорема 2. При выполнении неравенства

• I    ц-ац + 1 ц-а          |

а > max          ;£---ц - (ц - Щ

[ р 2 р               J нулевое решение системы (7) является асимптотически устойчивым.

Доказательство. Известно [6], что из асимптотической устойчивости нулевых решений изолированных подсистем (6) следует существование дважды непрерывно дифференцируемых однородных порядка Y 1 - Р + 1 и Y 2 - Р + 1 соответственно функций Ляпунова Уф 1 ) и У2ф), удовлетворяющих требованиям теоремы Ляпунова об асимптотической устойчивости. В качестве 7 1 и 7 2 можно выбирать любые рациональные числа, большие ц + 1, с четными числителями и нечетными знаменателями. Для возмущенной системы функцию Ляпунова строим в виде:

У(к,z) = V1(z1) + V2(z2) - яу А*           ( яу А*        °0

| С 1^{( к )} д 1⁽ ^2) -|1 ^С 2^{( к )} д 2 <А) ^-

9 ^z i )                ( S ^z 2 )

Функция (11) при к = 0,1, ... для всех z е Еп удовлетворяет следующим неравенствам:

• 2                    .

« 1 s и i^{Ys -} " ^{1 1} - « з ( 1^11 r^1-pii^2i г »

s = 1

₊ Р1| р |Z2| |^{Y 2 -Р} ) <  V( ^k , ^z > < « 2 f Psi |^{Ys-P+ 1} + s = 1

+ аз(|lz1 p Plz2 Г + P1IГP2IlY2 рX где й1,Й2,аз — положительные постоянные.

Вычислим приращение функции y(k,z) на решениях возмущенной системы. Получим ду = (Vt(xt(k + 1) - Vt(xt(k)) + (V2(x2(k + 1) -

Для четвертого получаем:

- V 2 (x 2 (k)) +

'( av.

[—¹ (x_t (k))| Q (k)g_v(x₂(k)) -

К 5zi       J ч *

—2 (x2(k)) B2(k)g2(xt(k)) -

8Z 2         J

^^^^^e

^^^^^e

*

A

^{a V} (xt (k + 1))| Q(k + 1)g_t(x₂(k + 1)) + dz,             J                           J

*

+

( av        A

—² (x₂(k)) C₂ (k)g₂ (x_t (k)) -

5z2

O 2 v

*

A

^{a V 2} (x₂ (k + 1))| C₂ (k + 1)g₂ (x_Y (k + 1)) .

Sz 2              J                         J

Распишем выражения в каждой из скобок. Первое слагаемое можно представить в виде

*

(avA

• -    —² (x₂(k)) C₂(k + 1) ( g₂(x_t(k + 1)) -

• V az2

KavA

—A2 (x2(k + 1)) I -az2

*

( av       AA

• -      ² (x₂(k)) I C₂(k + 1)g₂(x_t(k + 1)).

Vaz 2          JJ

Найдется H ^ > 0 такое, что при к >  0,

||x(k)|| < H1 справедливо соотношение:

/X

| —¹ (x ₁ (k))| Дг/к) +

Vaz1

+ ¹ (Ax_t(к)) [^Д ² (x^(к) + O^Ax(к)) | Ду (к).

2 V5zt2

Здесь Ax _t (k) = / ^ (x^k)) + ^(x(k)) + ^(k, x(k)).

Для второго выражения имеем:

AV < -Ь ₀ (||x _t (k)| |^Y ! + ||x ₂ (k)| |^{Y 2} ) +

+ b t <| ^_t (k)| |^Y 1 ^-ц+ “ ^₂ (k)| |^P + (| ^_t (k)| |^Y 1 ^{-ц- 1} +

+ (| ^_t(k)| p| |x 2 (k)| p ) ^Y i ^{-ц- 1} +

ч *

—2 (x2(к)) Дд2(к) + -(Ax2(к))* х az2

a2vA

----² (x ₂ (к) + 0 ₂ к Ax ₂ (к) ) I Ax ₂ (к),

5z22

где Ax ₂ (k) = / 2 (x ₂ (k)) + / ₂ (k,x(k)), 9_sk e (0,1), s = 1, 2. Третье слагаемое представим в виде: *

(A

• - —-(xt(k)) S₄ (k)g^ (x₂(k)) -

• V8z-J

* (avA

-1 —- ₁₁(k + 1) (g₁(x₂(k + 1)) -

V az1

K A

—- (x1(k + 1)) I - az1J

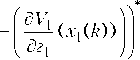
Q(k + 1)g _t (x ₂ (k + 1)).

+| Р1(к)| I^2a| р₂(к)| Г ^{2 -ц- 1} + 1 Р1(к)| p^{(y 2 -}^^{- 1)} х

X |д ₂ (к)| |^{2 ц} + ||д ₁ (к)|p^{( Y 2 ц+ 1)} ) + Ь ₃ (||д ₁ (к)| |^{Y 1 ц} х

X (| |д₂ ( к )| Р ¹ + |р₁ ( к )| р ^{( п 1)} )(| р₂ ( к )| р +

+ ||xt(k)|р) + (||xt(k)|р-ц-1 + ||xt(k)|P(Y1-ц-1) х х|P2(k)|p(Y1-Ц-1) +|P2(k)|P(Y1-Ц-1)) х x (||xt(k)|р + ||x1(k)|р ||x2(k)||Р + ||x2(k)||°) x x (|| x2(k)| P+l |xt(k)| p2 ) + b4(||x2(k)||Y2 -P x

X(||x₁(k)| p ¹ + ||x₁(k)| p^{( p 1)} ||x₂(k)| |^{P ( p 1)} +

+ p2(k)| |^{P( P 1)} )(|p1(k)|p + |p1(k)|p |p2(k)|p +

+ |x₂(k)|P) + (||x₂(k)||^{Y 2 p 1} + ||x₁(k)|P^{( Y 2 p 1)} )х

(| |т ₂ ( к)| ^р + ||^ ₁ ( k )|р(| Х ₁ ( к ) ° +

+ pa)||а“ ра)р + ра)^2 ) = W(х(к)), где Ь0, ..., Ь4 — положительныепостоянные.

Функция W(z) представима в виде W (z) = -b 0<| |р |⁷ 1 + ||z ₂||⁷ 2 ) + W 1 (z), где W ₁ (z) есть линейная комбинация функций вида IIЛ Г¹ 1^2 Р- Для существования окрестности положения z =0,в которой W(z) будет отрицательно определенной, достаточно [4], чтобы для каждой такой функции выполнялось следующее неравенство:

4 1 / 7 1 ⁺ 4 2 / 7 2 > 1.

Таким образом, получим систему ограничений на Y 1 , Y 2 , Р, Ф Р, °. Исключая из нее избыточные выражения, приходим к соотношениям:

7 1 >  Ц-« 7 1 >  Ц ^{+ 1} 7 1 >  Ц

7 2       ^р ’ 7 2      2а ’ 7 2 а ⁺ ц ^-1 ’

7 1 _<  2а 7 1 <а + ц -1         (12)

7 2 ^< Ц + 1 ’ 7 2 ^<  Ц '

Множество допустимых значений параметров Y 1 , Y 2 не является пустым, если выполнено условие теоремы.

Выберем Y 1 , Y 2 , удовлетворяющие неравенствам (12). Тогда для достаточно малых значений ||Х(к)|| и при всех к > 0 будут справедливы оценки:

“- 2 IMP Г⁵   ^иа, -^)) ^

• ² 5 = 1

^ “ 2 2 |^s(*)|Г^{5 +}

• ² 5 = 1

а у < - (|^а) |⁷ 1 + ^а) |^{7 2} ).

Следовательно, функция V(к,z) удовлетворяет требованиям дискретного аналога теоремы Ляпунова об асимптотической устойчивости [2]. Теорема доказана.

Пример. Рассмотрим систему

Х 1 (к + 1) = X i (k) - Xi (к) + x i (k)x ₂ ²³ (к),

Х ₂ (к + 1) = Х ₂ (к) - Х ₂ ³(к).

Нулевое решение системы (13) является асимптотически устойчивым.

Теперь рассмотрим возмущенную систему

Х 1 (к + 1) = Х 1 (к) - Х 1³ (к) +

+ Х 1 (к)х 2^{/ 3} (к) + ах2°(к) sin кк,    (14)

Х 2 (к + 1) = Х 2 (к) - Х 2 ³(к) + bX 1 ^а (к)cos кк, где а — положительное рациональное число с нечетным знаменателем, к, а, b — постоянные величины, к > 0.

В соответствии с теоремой 1 имеем, что при а > 18 нулевое решение системы (14) также является асимптотически устойчивым.

Последовательность Сг(к)(С2(0), С2(к) = к-1

= 2 BiO, к = 1, 2, ..., В 1 (к) = а sin кк, 5 = 0

В 2 (к) = b cos кк) является ограниченной, г = = 1, 2. Применяя теорему 2, получаем, что при а > 16 возмущения не нарушают асимптотической устойчивости нулевого решения. Следовательно, теорема 2 задает более широкую область допустимых значений для параметра а по сравнению с областью, задаваемой теоремой 1.