Об устойчивости решений сингулярно возмущенных обыкновенных дифференциальных уравнений

Бюллетень науки и практики / Bulletin of Science and Practice Т. 9. №3. 2023

УДК 517.928                                      

Вводим определений связанные с понятием устойчивости сингулярно возмущенных обыкновенных дифференциальных уравнений. Рассмотрим уравнения sx ’(t, s) = a (t) x (t, £ ) + £h (t)                                              (1)

x ( 1 ₀ , s ) = x⁰ x ⁰| = о (s )                                                 ⁽²⁾

где x ⁰ - const , \h (t )| <  C ₀ , C _o - const .

Решение задачи (1)-(2):

t

\

t

t

\

x ( t, s ) = x ⁰ exp — j a ( s ) ds + j h ( t )exp — j \ ( s ) ds d r I ^£ 1 0          J 1 0             к ^£ r           J

к

t 0

J

t 0

Определение 1. Если выполняются условия t0 < t < To (Re a(t) < 0), Re a(T) = 0, To < t < T ( Re a(t) > 0)  > Vt e [t0, T] (|x(t, s)| < M ). Тогда интервал [t0, T] для решения x(t, s) является затягиванием потеря устойчивости.

Пример 1. Пусть a ( t ) = t + i , тогда по определению 2 выполняется и t e [ - 1,1 ] будет устойчивым. Длина затягивание потеря устойчивости равна £ = T - T = 1 .

Определение 2. Если решения задачи (1)-(2) существуют на t ₀<  t <+г , ( t₀ = 0 не исключается) и ограничены, то решения (3) назовем, устойчивы вправо.

Пример 2. Пусть a ( t ) = ( t + i )^{- 2} и t₀ = 0 . Тогда Re a ( t ) >  0 , - г <  t < - 1 , 1 <  t < - г , Re a ( T ) = 0 , T _o =± 1 , Re a ( t ) <  0 , - 1 <  t <  1. Решение устойчиво вправо на t e [ 0, +г ) .

Определение 3. Если решения задачи (1)-(2) существует на - г <  t <  t₀ и ограничены, то это решения назовем, устойчивы влево.

Определение 4. Назовем решение (3) биустойчивым на полуоси t ₀<  t < + г , если оно устойчиво вправо и влево.

Из [5] известно, что если собственные значения состоит из чисто мнимых частей, то они устойчивы в действительной оси.

Пример 3. Пусть a ( t ) = 2 it . Тогда первообразная функция F ( t ) = it ² биустойчива на полуоси.

Определение 5. Если решения задачи (1)-(2) существуют для -10 < t < 10, (10   -г не исключается) и ограничены, то это решения назовем двухсторонне устойчивыми на [-10, t0 ].

Пример 4. Пусть a ( t ) = - 2 1 . Тогда фунция F ( t ) = - 1 ² двухсторонне устойчива на числовой оси. Все понятие по устойчивости связано с понятием устойчивости по Ляпунову [6].

Уравнения (1) с начальной задачей (2) оценивается в действительной области, когда только тогда, когда существует двухсторонне устойчивой прямой относительно числовой оси t . В остальных случаях решения неоднородных линейных дифференциальных уравнений (1) оцениваем, переходя к комплексной области.

• 2) . Двусторонне устойчивая прямая также существует относительно оси 1 ₂ . Покажем с помощью примера. Пусть a ( t ) = 2 1 , устойчиво t е ( -г ,0 ) , t = 0- точка смены устойчивости, t e ( 0, +да) — неустойчиво. В качестве начальной точки возьмем точки t₀ = 0 . Переходим к комплексной области. Тогда t = t_x + it₂ , r = r + i T , ( t i, t₂ T , t₂ ) e R , i = 4-1 . Определим область в комплексной плоскости H = {(^ , t ₂): F ( t j , t ₂) <  0, t ₂ >  0, -г <  t j <+г } , F 1 ( 1 1 , 1 2 ) = t ² - 1 2 ² , F 2 ( 1 1 , 1 2 ) = 2it 1 1 2 , H 2 = {( t 1 , 1 2 ) : F 1 ( 1 1 , 1 2 ) <  0, 1 2 <  0, -г< 1 1       < : . H = H 1 о H 2 .

Определим двухсторонне устойчивой прямая в комплексной плоскости. При t j = 0 имеем прямой относительно оси ордината или t . Эта прямая является частным случаем линии уровня [1]. С помощью этих прямых получим оценки решения (3). Имеем в H

|X j ( t_x , t₂ )| <  C4 s , 0 <  C - const .

Рассматриваемая область двухсторонне устойчивая относительно оси ординат. Прямая t j = 0 вертикально двухсторонне устойчивая прямая.

• 3) . Мы рассматривали горизонтальные и вертикальные двухсторонне устойчивые прямые. Теперь рассмотрим наклонные двухсторонне устойчивые прямые. Пусть a ( t ) = it . Действительная часть равна нулю. Поэтому переходим к комплексной области. Тогда t = t j + it ₂, т = т + T , i = 4-1 , ( t j , t₂ , t , T ) ^e R , u ( t i , t 2) = — 2^ t ₂, ^ (^ , t ₂) = 1 2 - 1 ₂ ² . Определим области S, = {(^ , t ₂): u ( t_x , t₂ ) <  0, t ₂ >  0, t_{ >  0 } , S₂ = {(^ , t ₂): u ( t_{ , t₂ ) <  0, t_{ <  0, t₂ <  0 } , t₀ = 0 .

Определим наклонно двухсторонне устойчивой прямая в комплексной плоскости. Прямая t₂ = kt_x , ( k -коэффициент наклонностью) наклонная двухсторонне устойчивая прямая, одновременно является частным случаем линии уровня [1]. Имеем в S

| x 1 ( 1 1 , 1 ₂)| <  C 4 s , 0 <  C - const .

Цель исследования. Исследуем решения сингулярно возмущенные нелинейные дифференциальные уравнения с начальной задачей, когда собственные значения Жордановой матрицы-функции определяют условия смены устойчивости.

Материалы и методы исследования

Рассматривается сингулярно возмущенных обыкновенных дифференциальных уравнений sx' (t, s) = J (t) x (t, s) + s[ h (t) + f (t, x (t, s))]                                            (4)

X ( t 0 , s ) = 0 ,                                                                    (5)

где 0 < s - малый параметр,  h(t) = colon(h(t),h,(t),...,hs,n,(t)) , s(n) = nn^ , n e N , t 0 = t 01 + it 02 , (t 01, t 02) e R , i =V-1 , f (t, x(t, S)) = colon (fКt, x), f,(t, x),..., fs ( n)(t, x)) ,

J ( t ) = diag ( J 1 ( A ( t )), J 2 ( A 2 ( t )),..., J s ( n ) ( A n ( t )) )        ,		где	J 1 ( A 1 ( t )) =	f A , < t )    0 1 1   1     A ( 1 ) J
f A ( t )    0      0   1 2	f A n ( t )    0      0	...      0 Л
	1     A ( t )    0	...      0
J 2 ( A 2 ( t )) =      1      A 2 ( t )     0     , ..., J s(n) ( t )	0     1     A n ( t )	...      0	.
1   0       1      A 2 ( t ) J          ()	...            ...            ...	...         ...
	k 0     0     0	...    A n ( t ) J

Для решения поставленной задачи от правых частей (4) потребуем выполнения следующих условий:

U1. f ( t ,0) = 0 , f ( t , ~) - f ( t , ~ )|| <  M X ~ - ~ 1, 0 <  M - некоторая постоянная.

U2. Re A _k ( t ) >  0 , -^ <  t <  T ₀ ; Re A _k (0) = 0 ; Re A _k ( t ) <  0 , 0 <  t <+«, k = 1,2 .

U3. Re A _k ( t ) = 0 , A _k ( t ) = в ( t ) , k = 3,5 .

U4. Re A ( t ) >  0 , -«< t <+« , k = 6,10 .

U5. Re A ( t ) <  0 , - T <  t <  T ; Re A ( T ) = 0 ; Re A ( t ) >  0 , T <  t <  T , T >  0 , k = 11,12,... .

U6. F_k ( t ) = Re J A ( s ) ds , F k ( 1 0 ) = 0 , k = 1,2,... .

t 0

Среди собственных значений Жордановой матрицы J(t) могут быть кратные комплексно собственные значения.

Имеет место следующая теорема:

Теорема. Пусть выполнены условия U1-U6. Тогда в области G решение задачи (4)-(5) существует, единственно и для него справедлива оценка

II x ( t , £ )|| <  C £ , 0 <  C - const

Доказательство. Задачу (4)-(5) заменим следующим эквивалентным интегральным уравнением

t

x ( t , £ ) = J V ( t , T , £ ) X [ h ( t ) + f ( t , x ( t , £ )) ] d

¹ 0

' t exp J\jn (A(s d

I ^£ T

1 t                             '              1 t где V(t,т,£) = diag exp —JJ1(A1(s))ds ,exp —JJ2(A2(s)ds

t

t

t

,...,

.

к

Для доказательства существования решения уравнения (7) применим последовательных приближений.

метод

Последовательные приближения определим следующим образом:

x о ( t , £ ) = 0 ,

t

x m ⁽ t , ^£ ) = J ^{V (} t , Т ^£ ) ^X [ ^{h ( Т} ) ^{+ f (} Т x m — 1 ⁽ Т ^{£ )) ] d T} 0

где x m ⁽ t , ^£ ) = colon ⁽ x m ⁽ t , ^£ ), ^x 2 m ⁽ t , ^£ ),

I ...

, x s ( n ) m ⁽ t , ^£ ) ) , m = ^

I ...

, s ( n ) = nn m , n e N .

Определяя пути интегрирования lm , ( m e N), m приближения и соединяют точки (t0,0) с точкой (tj; t2) . Пути интегрирования проходит по двухсторонне устойчивой прямой. Для первого приближения имеем по компонентам

I x s ( k ) ( t , £ )| <  C £ (1 + C 1 + ... + C s ^{( k ) — 1} ) , s ( k ) = ^{k ( k} + ¹⁾ ,

k = 1, n . x s _{( k} )1 ( t , £ )| <  C £ (1 + C 1 + ... + C s

-s ( k ) - 1

) , или

I x s ( k )1⁽ t , ^£ )| <  ^C

1 — C s ^{( k} )

1 — с ~ ^{£ q}s ^{( k} )

1 _— c^s ( ^k )

где q (kj = C----1—. Постоянная Cx > 0 и возможны случаи 0 < C < 1 или C > 1 . Без s (k)          1 — c1                               1                                                       1                   1

ограничения общности можем считать, что C > 1. Тогда q_{s(k }}<  q_m = C .

И так в силу оценки (12) вытекает, что для решения задачи (4)-(5) справедлива оценка

||x_{ (t , £ )|| <  C £ . t e G

Пусть

IIxm(t,£)|| < а(£), t e G где am (£) - некоторая положительная функция от £ , а1(£) = C .

Оценим x_{m + 1} ( t , £ ) . Имеем

|^X 1( m + 1)

( t , £ )| <  I * ii ( t , £ )| + f ^exp ^f - ( F ( t ) ^- F ⁽ t ) ) ] x | f _ ( t , X m ) ^- f 1 ( t ,0)| d т <  C £ + C s 2 a_m ⁽ s ) . < ^s               J

l

m

|^X 2( m + 1)

⁽ t , ^£ )| <  x 21 ⁽ t , ^£ )| ^{+ 1} f ^eXP l ^{1 ( F} 2 ⁽ t ) — ^F 2 ⁽ T ) ) I ^X | ^sL У ^£              J

I,

m

\^X 1( m + 1)

⁽ T ^£ )| + f exp f ^{1 (} F 2 ⁽ t ) ^- F 2 ⁽ T ’Й ^{У £ J}

I,

m

X

x| f Pt X m ( t , s )) - f ₂( t ,0)| d T <  C s + ¹ ( C s + C S²a_m ( s ) ) x C s + C s ² a_m ( s ) =

= C s + C ² s + C ² s ²a_m ( s ) + C s ² a m ( s ) .

Без ограничения общности считаем, что C >  1. Тогда

|^X 2( m + 1) ⁽ t , ^s )| < ^{2 C s + 2 C s a} m ^{( s} ) .

|Xs ( k _w.1, ( t , s ) <  s ( k ) C S ⁽ ‘ s + s ( k ) C ’“ ’ s'a . s )                              ⁽¹²⁾

Оценка (12) верна при k = 1,2 . Тогда

I ^X ( s ( k ) + 1 )( m + 1 ) ⁽ t , ^s ’ <  ^X ( s ( k ) + 1 ) 1

⁽ t , ^s ’| + ¹ J exp l ^{1 (} F_s ( k ) ⁽ t ’ ^- F s ( k ) ( ^T ’) || ^X s ( k ) ( m + 1 ) ^{( T} , ^s ’ ^{d T s} L У ^s                 J

+

I,

m

+

f exPf 1 (Fs(k’ (t’ - Fs(k) (t’)] X |fs l Уs                       J

m

s ( k ) + 1

^{( T} , ^X m ^{( T} , ^s ’’ ^{- f} s ( k ) + 1 ^{( t ,0)}| ^{d T}

<

< C s + ¹ ( s ( k ) C ^{s ( k} ’ s + S ( k ) C ^{s ( k} ’ s ² a_m ( s )) C s + C ea_m ( s ) <  s

< ( s ( k ) + 1) C s ^{( k ) + 1} s + ( s ( k ) + 1) C s ^{( k ) + 1} s²a_m (s ) .

Доказано справедливость оценки (12) для любого s(k). Таким образом, из (12) следует, что

IXs(k)(m+1)'t, s’ < s'k’Cs'k’s + s'k’Cs'k’s^m's’ = sam+1's’ , t G G(13)

где a m _{+ 1} ( s ) = s ( k ) C s ^{( k} ’ + s ( k ) C^{s ( k}’ sa _m ( s ), k = 1, n . Справедливость оценки (10) доказана.

q - s ( k ) C ^{s ( k} ’

Введем обозначение q = (s (k) +1) C() , тогда из (12) при условии s <———

s(k)Cs(k)q следует, что Vm g N : am (s) < q. Если учесть (11), то получим ||Xm (t,s’ll < qs , t G G

Теперь докажем сходимость последовательность приближений.

Пусть

IIXm (t, s’ - Xm-1 (t, s’ll < sPm (s’ , t G G

Оценка    (15)    верна     m = 1    ,    причем     в ( s ) = C    .    Имеем

| ^X 1( m + 1) ⁽ t , ^s ’ - ^X 1 m

⁽ t , S ’| <  f expf^{1 (} F S ⁽ t ’ ^- F S ^{( т} ' ’Й ^f 1 ^{( т} , ^X m ’ ^{- f} K T ^X m - 1 ’| d ^{T У s J}

< ^ ² P m ( s ) .

l

m

|^X 2( m + 1) ⁽ t , ^s ’    ^X 2 m

⁽ t , ^s ’I <  ¹ j exp ^{f 1 ( F} 2 ⁽ t ’ - ^F 2 ⁽ T ’ Й ^X | ^sL У ^s              J

I,

m

|^X 1( m + 1) ^{( T} , ^s ’ - ^X 1 m ^{( T} , ^s ’|

+

+

J exp I ¹ ( F ( t ) - F 2 ( T ) ) | X | f 2 ^{( т} , x m ) - f_г( т , x m - 1 )| d T l m     ^ ^{£                  J}

<

< 1s2em (s)C2s + s2em (s)C2^ = 2C2s2em (s). s

|x 3( m + 1) ⁽ t , ^S )    x 3 m

(t, s)! < 1 J eXP11 (F3 (t) - F3 (T))] X I'

l

m

+

I x 2( m +1) ( ^T , ^s ) - x 2 m

+

J ^ex p l ^{1 (} F 3 ⁽ t ) ^- F 3 ^{( t} ) ) ] ^X | f 3 ^{( T} , x m ^{( T} , ^s )) ^- f 3 ^{( T} , x m - 1 ^{( т} , ^s ))| d ^T l m    ^ ^{S                 J}

<

I x s ( k )( m + 1) ( t , ^s )    x s ( k ) m

+

< ¹ s ² P m ( s ) C 3 s + s ² P , ( S ) C 3 S = 3 C 3 S 2 P m ( S ) . s

⁽ t , ^s )l <  ¹ J ^^{1 ( F}^ ( k ) ⁽ t ) - ^F s ( k ) ^T ) ) ] ^X I

l

m

J exp| 1 (Fs(k) (t) - Fs(k) (T))l X | fs(k) T lm     ^s                       J

| xs ( k )( m + 1) ^{( T} , ^s ) - x s ( k ) m ( t , s )| d T +

, x m ( ^T , ^s )) ^- f s ( k ) ⁽ T x m - 1 ⁽ T ^s ))| ^{d T}

<

< ¹ s ² P m ( s ) C ⁽ ‘) s + s ’² P m ( _S )C s ⁽ k ) s = s ( k ) C s ⁽ k ) s 2 P m ( s ) . s

Применяя метод математической индукции нетрудно доказать справедливость оценки

I x s ( k )( m + 1) ⁽ t , ^s ) - x s ( k ) m ⁽ t , ^s )| <  s ^{( k} ) ^C s ^{( k ) s2}P m ^{( s} ) , ^k = ¹ n •

Таким образом, оценка (15) верна причем

V m € N в ( s ) = s ( k ) C ^{s ( k} ) se _m ( s )                               (16)

,

Из (17) при условии s ( k ) C^{s (} k ) s <  1 следует, что последовательность функций { x_m ( t , s ) } в G равномерно сходится к некоторой функции x ( t , s ) е G . Эта функция является решением (7). Если учесть (14), то справедлива

||x(t, s)|| < sq t € G                                                 (17)

Докажем единственность решения. Допустим, что существует другое решение x ( t , s )

задачи (7).

t

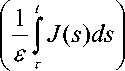
d T .

y(t,s): y(t,s) = J[h(t) + f (t, x (t, s )]x exp t 0

t

( T , s )) - f ( t , x ( t , s )) ] exp -Re ^ s

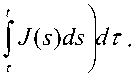
I x s ( k ) ⁽ t , ^s ) - У ⁽ t , ^s )|| <  J ^{[ (} f ^{( T} , x m - 1

t 0

Предположим

II x s ( k ) ( t , ^s ) - У ⁽ t , ^s )|| <  ^{s ( k} ) ^C s ^{( k} ^Prn ^{( s} ) •

По методам математической индукции

I x , ( k ) + 1 ( t . s ) - У ( t , s )|| <  ( s ( k ) + 1) C s ⁽ k ^{) + 1} sPm + 1 ( s ) .

Таким образом, Vm g N , ||y(t, £) - x(t, £)|| < 0  ^   x(t, £) = y(t, £) . Единственность решения доказано. Теорема польностью доказано.

Результаты и обсуждение

В ходе исследований обнаружены новые виды устойчивых областей [5-6]. Название новых областей даны в вышеперечисленных определениях. Двухсторонне устойчивые прямые, применим при выборе пути интегрирований. Эти двухсторонне устойчивые прямые является частными случаями линии уровня [1].

Если собственные значений Жордановой матрицы состоит из чисто мнимых частей, то эти собственные значение порождают двухсторонне устойчивые области [5] в плоскости.

В работах рассматривались случаи, когда собственные значения состоящих чисто мнимых частей [2-3] и собственные значения, порождаемые устойчивости влево и вправо [4]. Но тогда нам не было известно такие виды устойчивости.

Выводы

Виды устойчивости зависят от собственных значений Жордановой матрицы. Если Л ( t ) = ib ( t ) тогда эти собственные значения порождают в комплексной плоскости двухсторонне устойчивые области. А также действительная ось будет устойчивой, если собственные значения состоит из действительных частей, то при благоприятных случаях появится двухсторонне устойчивые области.

Если собственные значения состоит чисто мнимых частей, тогда комплексной области смены устойчивости проходить через ось t .

Действительные части собственных значений Жордановой матрицы функции в двухсторонне устойчивой области меняет смены условия устойчивости.