Объединенный метод конечных элементов Галеркина и граничных элементов для анализа дифракции ТМ-поляризованной плоской волны на цилиндрических оптических элементах

Для задач моделирования дифракции света на оптических элементах с размерами порядка длины волны свет должен рассматриваться как электромагнитное излучение. Основная часть численных методов моделирования дифракции могут классифицироваться как дифференциальные [1], разностные [2,3], интегральные [4-8], вариационные [9-12], дискретных источников [13], рассмотрение хода лучей [14].

Для определения электромагнитных полей в точке пространства интегральные методы объединяют вклады в эту точку от поля источников по объему или на поверхности. Популярность интегральных методов основывается на их способности решать неограниченные полевые задачи, т.к. условие излучения Зоммерфельда безусловно удовлетворяется в формулировке задачи. Более того, интегральные методы требуют знания поля только на поверхности дифракционного элемента, а не полного поля в пространстве, что минимизирует число неизвестных. В работах [15, 16] представлен объединенный метод на основе метода граничных элементов. В [17] разработан метод расчета дифракции на плоскопараллельной пластине с неоднородностью на основе интегральных уравнений, связанный с численным решением тензора Грина. Недостаток таких методов в том, что они приводят к полностью заполненным матрицам и, следовательно, требуют большего объема компьютерной памяти и длительного времени вычисления. Также границу применения методов необходимо брать по физической границе объекта. Если неоднородность имеет нетривиальную форму, то это приводит к увеличению числа неизвестных.

Разностное решение дифференциальных уравнений Максвелла рассматривалось в работах [18-21, 3]. В работе [22] описано разностное решение волнового уравнения. Недостатками такого подхода являются невозможность использования условий излучения, ограничения на шаги сетки. Для моделирования стационарных задач прохождения излучения разностными схемами используется конечное количество длин волн падающего импульса, что искажа- ет спектр волны. Использование в качестве граничных условий для неограниченных задач дифракции условий поглощающей границы [23,10] позволяет приближенно решать уравнения Максвелла разностными схемами, точность решения зависит от количества слоев на искусственной границе и от степени ее замкнутости.

В отличие от методов разностного решения системы уравнений Максвелла интегральные и вариационные методы не требуют конструирования сложных поглощающих граничных условий [2, 10].

Вариационные методы в задачах с ограниченной областью задачи определяют решения уравнения Гельмгольца путем минимизации функционального соотношения. В работе [10] уравнение Гельмгольца решалось методом конечных элементов Галеркина с использованием граничных условий сложного вида, зависящих от неизвестного параметра, что потребовало применение границы, определенной формы. Кроме того, данный метод также не включает в себя условия излучения Зоммерфельда.

В работе [24] представлен гибридный метод на основе метода конечных элементов, сформулированного через метод Ритца, и метода граничных элементов. В данном гибридном методе метод конечных элементов применяется для решения уравнения Гельмгольца во внутренней части неоднородного элемента микрооптики, и применяется интегральная методика, метод граничных элементов - к области, внешней к элементу микрооптики, где должны удовлетворяться условия излучения. Оба метода соединяются на границе между внешней и внутренней частями, с удовлетворением условий непрерывности поля. Использование метода конечных элементов для определения поля внутри объекта приводит к матрице трехдиагонального вида, что требует меньше компьютерной памяти и времени вычисления, чем методы объемных интегралов [25]. Результатом использования метода граничных элементов для определения поля на границе является более точное решение, чем применение метода конечных элементов с условиями поглощающей границы. Но применение метода Ритца к решению уравнения Гельм- гольца некорректно, т.к. он накладывает требование положительности оператора решаемого уравнения. Вывод о знакоопределенности оператора уравнения Гельмгольца сделать нельзя.

В предыдущих работах авторов [26-28] разработаны методы анализа и синтеза элементов двухмерной (цилиндрической) микрооптики, основанные на объединенном методе, который объединяет метод конечных элементов Галеркина (МКЭГ) и метод граничных элементов (МГЭ) для случая ТЕ-поляризации. В данной работе приводится разновидность объединенного метода МКГЭ-МГЭ для случая ТМ-поляризации.

Описание метода расчета для случая ТМ-поляризации

Для TM-поляризации комплексная амплитуда u ( x , y ) обозначает полное магнитное поле H z ( x , y ), которое направлено вдоль оси z (вдоль образующей цилиндрического оптического элемента), координаты (x,y) лежат в плоскости нормального сечения. Полное поле u ( x , y ) представляет собой сумму рассеянного поля u sc ( x , y ) и падающего поля u inc ( x , y ).

Полное поле u _Q ( x , y ) в Q (внутренняя область без граничных точек) должно удовлетворять уравнению Гельмгольца:

_        1 d u_n ( x , y ) d u ( x , y )

где g (x, y)=--,--, при (x, y) € Г s   dn        dn для ТМ поляризации и при условии прохождения границы Г по линии раздела сред (объект и внешнее пространство).

Таким образом, требуется определить полное поле u ( x , y ) в областях Q (внутренняя) и V (внешняя), удовлетворяющее указанным условиям.

Метод Галеркина вместо решения уравнения

Гельмгольца (1) основан на решении соотношений вида:

JJ I - “ ^А [ u Q c + u Q c ] y - qk ² [ u Q c + u Q c ] y I d Q = 0, (6)

p                           j

где y - произвольная функция из области определения уравнения (1).

Используя первую формулу Грина:

U P А Q d Q = J PdQ dl - JJ V P V Q d Q ,

Q           Г ^d n      Q

для функций P и Q , где Q - область плоскости x, y; Г - ее граница, обходимая против часовой стрелки;

dQ d n

- производная в направлении внешней нормали

V-

1 p ^{( x} , y )

^V u Q ⁽ x , y )

+ k 0 ² q ( x , y ) u q ( x , y ) = 0 ,

где p ( x , y ) = p r и q ( x , y ) = s r для TE поляризации и p ( x , y ) = s r и q ( x , y ) = p r для TM поляризации. Константы p r и s r представляют собой отношение магнитной и диэлектрической проницаемостей среды к аналогичным показателям свободного пространства, т.е. p r = p / p o и s r = s / s ₀, к ₀ представляет собой волновое число волны в свободном пространстве:

к о = ю ( ц о Б о ) ^1/2

го 2 п

=      .

С ^ 0

Таким образом, обе поляризации удовлетворяют уравнению (1), но с использованием замены переменных:

^E z ^ H z-, ^P ^ S r , S r ^P r .

Так как падающее поле u inc ( x , y ) известно, то уравнение (1) должно быть решено для рассеянного поля u sc ( x , y ).

Рассеянное поле u sc в свободном пространстве ведет себя в соответствии с условием излучения Зоммерфельда

\u = ikо usc (4) dn на бесконечности и удовлетворяет уравнению Гельмгольца (1) во внешней области с граничными условиями вида:

d u sc   _

= g d n

к кривой Г , получим:

JJ I - V [ u Q c ( x , y ) + u Q ( x , y ) ] Vy - qk² [ u Q c ( x , y ) + "Q I p

+ u Q ( x , y )] y ) d Q-

-

г y d ^[ u Q c ⁽ x , y ) + u Q c ⁽ x , y ^)] •--d Г =0.

Г p        d n

Разделяя переменные, можно записать:

| - V u Qc (x, y) Vy - qk2 u Qc (x, y) y | dQ -p                        J ry du Qc(x, y)d Г =

Г p   d n

= JJ I - V u Q nc ( x , y ) Vy - qk² u Q nc ( x , y ) y I d Q +

^JQI p                             J

r i du Q nc ⁽ x , y )

l                                                                                                           .

Г p   d n

на поверхности Г ,

Систему базисных функций для Q обозначим { ® ^Q _k , l ( x , y )} " x i = N y и систему базисных функций для Г { J m ⁽ x , y ^)} M =i обозначим ^{ ® Г ( k , i ) ⁽ x , y ^)} ’M , _к , । )=i , где f ( ^k , l ), однозначно сопоставляющая точке ( x _k , y l ) точку на Г с порядковым номером m , может иметь вид:

l ,      если k = 1

f ( k , l ) = J

N + k ,

3 N + 2 - 1 ,

если 1 = N и k * 1

если k = N и 1 * N

4 N + 2 - 1 , если k = N и 1 * 1 и 1 * N .

Подставляя в соотношение (8) вместо произвольной функции y систему базисных функций для

метода Галеркина можно записать систему линейных уравнений:

A u sc + B v sc = - (A u inc + B v inc ), (10) где u= ( u 1 , ..., u ₍ N _{+ 1) 2}) T - вектор, составленный из коэффициентов { u _Ny ( k ) _+l = u k , l } N x , N^y разложения:

Nx, Ny uh(x, y) = Е uk,, mQ,,(x, у).                    (11)

k , l =0

Хотя равенство (11) действительно для всех точек ( x , у ) в Q , необходима отдельная обработка величин поля и его частных производных на Г от значений во внутренней области. Разложение, аналогичное (11), для поля и его частных производных на границе имеет вид:

u hr tA у) =

^mQ , l ( ^x , у ) =

	1 -	x k - h	x	- у1 - у h ,			если x, у е Q hUA
	1	x k - h	x				если x, у е Q k, l 2
= —	1 +	у 1 - h	y				если x, у е Q k, t3	(16)
	1 +	x k - h	x	+ у!	- h	y ,	если x, у е Q k, l 4
	1 +	x k - h	x	,			если x, у е Q y5
	1 -	у 1 - h	y	,			если x, у е Q y6

В силу симметрии A , трехдиагональности мат-

N x . N y                     M

= Е u k , i ®^r i ^{( x} , у )= Е ^u _f -'( У, ^{( x} , у )’    ⁽¹²⁾

о                     m — f ⁽ m ) f ⁽ m )

риц    { A_kk } N '_₁    и двухдиагональности матриц

M vh(x ,y )= е vm ®m(x, у), m=1

AN

^{{ k} - ^{k - 1 }} k =2

^N - ¹

и { A_{kk + 1}} _ достаточно указать формулы V , z k —1

где ( x , у ) е Г, v= ( v 1 , ..., v_M ) T - вектор, составленный из коэффициентов разложения { v m = v^_k , l ) } N x = N^y , v - ^d uk V_k .

k   d n

Элементы матрицы А вычисляются по формулам:

для вычисления элементов:

k,l k,l-1       k-1,l       k-1,l+1 i а k, l, а k, l , а k, lA а k, / , 1^k,l^N■

Эти формулы, согласно (14) и (16), имеют вид (для простоты используются обозначения Q i = Q k - l - , .):

a Ny(k)+l, Ny(i)+j

Q¹ _x P ⁽ x , у )

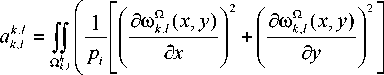
7 2 П ^{2 - k} » q i ^m k, l

d®^Q , i ( x , у ) ^dm j x , у ) + d x       d x

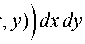
₊ dto ^i ( x , у ) dm “( x , у ) d у        8 у

1 h ²

IT —— d^xdy + IT —— dxdy +

Q , UQ ₂ ^p 1,2          Q ₄ U? ₅ ^p 4,5

^- k 0 ² q ^{( x} , у ^{) m} ?, i ^{( x} , у ^)m " ^{( x} , у ) ) d ^Q ,

+ IT —— dxdy + IT —— dxdy Q ₃ U Q ₄ ^p 3,4          Q , U Q ₆ ^p 1,6

k , i = 1,..., N x ; l , j = 1,..., N y , где Q _kj - треугольная область, включающая узлы сети k и j .

Элементы матрицы В вычисляются по формулам:

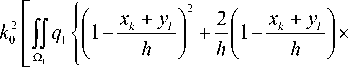
b m , p =- Т ® m m ' p ®> dl ,

1              \2 I

x ( x + у ) + h 2 ( x + у ) dxdy +

m , p = 1, ..., M , где Г _т , _p - линейная область границы Г , включающая узлы границы m и p .

Введем обозначение а 'j = a _Ny ( _k ) _+l , _Ny ( i ) + . Матрица А является блочной трехдиагональной .

Каждая из матриц A _k . _k является трехдиагональной матрицей порядка N . Более точный анализ показывает, что матрицы { A k ,_ы} N =2 и { A k , k+i } N^- - двухдиагональные.

Вычислим элементы ( а k’-j ) матрицы А и элементы ( b m , s ) матрицы В для частного случая кусочнолинейного базиса вида:

⁺ff q 5

? 5

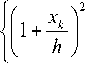
h

⁺ JJ q 6 il ¹

? 6      [x

a k,l ^{l - 1} — JJ

Q 11 ^Q k.

Гт x_k )

1 +

I h

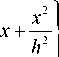
dxdby +

, 2

1 P dm Q l ( x , у ) 8to k ,

I ^p i

8 x

'-1 ^{( x} , у ) + 8 x

+ ^dmQ l ^{( x} , у ) ^dmQ l -1 ^{( x} , у )

8 у         d у    _

- k о ² q i ® ^Q l ( x , у ) m^Q , l -1 ( x , у ) ) dxdy —

—у JJ —— dxdy - k ₀ ² х h Q ₁ U Q ₆ p 1,6

х If , -      If , + x^ 1+ 1 f l +) x +

¹ К h Л h J h I h J _ ⁿ 1

1 f Xk + X / + X 11      1

+ - _k—У.—-   y--yx + y2 dXddy + h ( h J   hЛ       'J

b m,m-1 ф ® m ® m -1 dl Г k , l

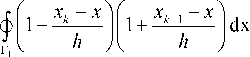
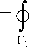
^{( x} - x k -1 ⁾⁽ x k - ^x ) h

dx = — h , 6

+JJ q 6 111 + q,   A

xk ⁺ У / -1 У / 1

h JI h J

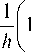
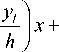
b m , m +1 b m , m -1 -

Тогда вместо системы уравнений (10) получим:

1 f x_k + y, + y,_ , 1       1 /         2\1 . .

⁺ h I ^k _h J y - h ⁽ yx ⁺ y ) j y

a k , l

q k , /

JJ

f 1

^q k -у

I p

S^ nMyX 5®ⁿ -1, / ⁽ x , У ) ₊ d x        d x

+222x21 s^ n-^ xiyl

d y

d y

- ^k 0 q ® ^Q , i ^{( x} , У ) х

х ®^Q_{- 1} l ( x , y ) ) dxdy = —у JJ —— dx dy - k ₀ ² х ^h Q ₁ U Q ₂ p 1,2

х

JJ q

. П1

7 xk + X 1fi xk- 11 1 f 1 x_k_ 11

1 - ——— 1 + - k -¹ +— 1 + - k -¹ y + h JI h J h I h J

₊ 1 I xk ⁺ xk -1 ⁺ Уi h I h

1      1 I x —d [xx + x

J   h^Л

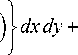
n ff, xk- 1+ Xt 1fi xk 1 1 fi xk 1

q j 1 +           1          1 + y +

² L h JL h J h I h

1 f x_t + x_t , + y , 1       1 /         , J , ,

+ - — ——— x —r yx + x2 \dxXx h ( h J h2V        7J

Элемент a k'l ^{+ 1} находится по формуле для вычисления a k■ / ^{- 1}, но интегрирование производится по областям Q k l ₃ и Q k l ₄ , элемент a ^k k +’- ¹ находится по формуле для вычисления a k -^{11 1} , но интегрирование производится по областям Q h l ₄ и Q k l ₅ , элемент а ^к_к + ^{11 1 - 1} находится по формуле для вычисления a kk -^{11 1 + 1}, но интегрирование производится по областям ^Q k , / ,5 и ^Q k , / ,6 -

Отсюда сразу следует, что матрицы { A _k , _k-1 } N_{= 2} и { A _k , _k+1 } N - ¹ являются диагональными. Элементы матрицы В вычисляются по формулам:

b m,m ф ® m ® m Г k , l

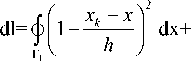
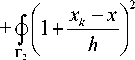
dx = 2h, 3

’[ A s , s J [ A r, s J 0 [ A s ,r J [ A r,r J [ B ]

[ A s , s J [ A r, s J [ A s ,r J [ A r,r J

[ B ]

sc

S

u Г sc

inc uS u n v n

В равенстве (19) коэффициенты связи между значениями поля только во внутренних узлах представлены подматрицей [A _s ,_S ] размерностью ( N-M) л ( N-M), где N - количество узлов разбиения области Q , M - количество узлов на границе Г . Связь между величинами поля только на граничных узлах представлена подматрицей [А Г , Г ] размерностью M x M, и связь между величинами поля на внутренних и на граничных узлах представлена подматрицей [А Г , _s ] размерностью ( N-M) х M и транспонированной [А _s , Г ] размерностью ( N-M) х M . Взаимодействие между производными величин поля на граничных узлах представлено подматрицей [B] размерностью M х M .

К сожалению, система уравнений (19) не имеет единственного решения, так как она состоит из N равенств с N+M неизвестными: N узловых величин поля u sc_k , l ( x , y ) и M производных по нормали на граничных узлах v sc_k , l ( x , y ).

Для построения граничного интегрального уравнения для поля и его нормальной производной воспользуемся теоремой Грина в следующем виде:

J [V ² u * ( ^ , n ) + k ² u * ( ^ , n ) J u ( n ) d Q ( x ) =

Q

= - J q ( n ) u * ( ^ , n ) d Г ( x ) + J u ( n ) q * ( ^ , n ) d Г ( x ).

Г                         Г

Функции в обоих интегралах в правой части

du (n) уравнения (20) - это q(n) =--нормальные про- dn

изводные амплитуды поля.

Пусть функция u является фундаментальным решением уравнения Гельмгольца:

V ² u * ( ^ , n ) + k ² u * ( ^ , n ) = -5 ( § , n )-              (21)

Фундаментальное решение для уравнения Гельмгольца в двумерном однородном пространстве известно и равно

u * = ( i /4) H 0 ¹⁾( kr ),

где r = V [ ^Х 1 ⁽ П ) - x 1© ] 2 + [ x 2 ⁽ П ) - x 2 < ^ ) ] ² ■ H 01 ^{) (} r ) = J 0 ( r ) + iY 0 ( r ) – функция Ханкеля первого рода и нулевого порядка, где J 0 – функция Бесселя первого рода нулевого порядка, Y 0 – функция Неймана нулевого порядка.

Подставляя равенство (21) в уравнение (20) и осуществляя предельный переход точки наблюдения ξ из внутренней в граничную, найдем c © u © + Ju (n) q * © П) d Г( x) = r (23)

= J q ( n ) " © n ) d Г ( x ). г

Это уравнение обеспечивает функциональную связь между функцией u и ее нормальной производной q на границе Г. Функция c в уравнении (23) равна:

c © = 1 - ;1 Ф ■ 2 n

где φ - внутренней угол кусочно-линейной границы в точке £ .

Подставляя вместо функции комплексной амплитуды на границе ее аппроксимацию базисными кусочно–линейными функциями, получим вместо (23):

_p em ■ s =^{+ h} J ® ^r ( ^c ■ ^{+ [ c} ■ +1 - ^c ■ ^] Y ) ^X e ms             о

^X " ‘ ^{( c} m ■ ^c s ^{+ [ c} s +1 - ^c s ^] Y ) ^d Y +

+ J ® Г ( c s -1 + [ c s - c s -1 ] y ) x

^X "  ‘ ^{( c} m ■ ^c s -1 ^{+ [ c} s - ^c s -1 ^] Y ) ^d Y] .

Интегралы в равенствах (27) и (28) могут быть оценены численно.

Принимая во внимание скачок нормальной производной поля на реальной границе рассеивающего объекта для падающей ТМ поляризованной волны v1 _v2 v;"c + vsc _vinc + vsc

£1" e2 ■     61     " e2     ■ и полагая для определенности относительную диэлектрическую проницаемость внешней к объекту среды ε2 = 1, и учитывая равенство v1inc = v2inc, можно записать inc           inc

_ £1    c   £ 1 v 2 -£ 2 v!

v 2 ⁺

^£ 2                ^£ 2

cmum =E h i" usc J0 ®г (ps+fo+i - ps ]y) x s=1    vL u"(p- ■p + [c ■+'- с ■]Y) d y + dn’

⁺ u sc J 0 ®^Г ( ^c ■ -i ^{+ [ c} ■ ^{- c} ■ -i ^] Y ) ^X

Xd" ‘ (C m ■ с ■ -1 + [C ■ — с ■ -1]Y) dY - an’                 L

или

sc

s

J ю ^г ( с ■ ^{+ [ c} ■ +i

- с ■ ^] y )^x

^X "  ‘ ^{( C} m ■ с ■ ^{+ [ C} ■ +1 ^- с ■ © ^d ^ ⁺

v sc =£ 1 v 2 ^c + ( £ 1 - 1) v ^inc

_v s ₂ c

v sc - ( £ 1 - 1K ^c

£ ₁

Тогда, объединяя системы уравнений (19) и (26), получим замкнутую систему линейных алгебраических уравнений для решения задачи дифракции плоской ТМ поляризованной волны на двухмерном (цилиндрическом) диэлектрическом элементе

микрооптики:

+ J ю Г ( c ■ -1 + [ C ■ - c ■ _Jy ) x

X "  * ( c m ■ C ■ -1 + [ c ■ - c ■ _Jy ) d y] } ,

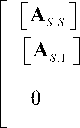
L A r_ $ ] ⁰ L A r.r ] ^[ B ^]

[ D ]   7 [ E ]

£ ₁

u

sc S

urc vsc

m = [ 1, M ] .

Равенство (25) может быть представлено в матричном виде:

[D] и Г ^с +[E] v c = 0,                          (26)

где элементы матриц [D] и [E]:

^d m,s =- h J 0 ^Юr ( ^c ■ ^{+ [ c} ■ +1 - ^c ■ ^] Y ) ^X

_X ^d " * ^(c m ■ ^c ■ + ^{[ c} ■ +1 - ^c ■ ^] Y ) d d n ’             ^Y

- h j 0 ®^r ( ^c ■ -1 ^{+ [ c} ■ - ^c ■ -1^] y )^x

_Y ^d " ‘ ^(c m ■ ^c ■ -1 ^{+ [ c} X---------------- d n ’

-

^c s ^-1® dY + c 5 , ^Y m ms ■

L A $ . $ ] L A $ .г ]

L ^А г $ ]     ⁰

L A г,г ] ^{[ B ]}

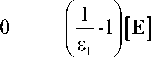
v

где $ - это область Q без своей границы Г_$ подматрица А _{S , S} размерностью N x N включает в себя коэффициенты вкладов внутренних узлов, подматрицы А _{S ,Г} и А _{Г, S} размерностью N x M и M x N соответственно включают в себя коэффициенты вкладов внутренних и граничных узлов, подматрица А Г, Г размером M x M включает в себя коэффициенты вкладов граничных узлов, u S и u Г – вектора напряженности поля во внутренних и граничных узлах сети.

Система линейных уравнений (30) может быть представлена в матричной записи:

Tu ^sc =Uu ⁱⁿ ,                                   (31)

u ^sc =T^-1Uu ⁱⁿ ,                                    (32)

где u ^sc =

usSc u?

v

u ⁱⁿ =

uS uin

v

для случая ТМ поляризации

T=

[ A s , s ] [ A r, s ]     0

[ A s , _r] [ A _r , _r] [ B ]

0       [ D ]   -1 [ E ]

^£ i

[ A s , s ]

U = -

[ A s ,r ]

[ A r, s ]      0

[ A r,r ] ^[ B ^] 0      f — - 1 ) [ E ]

l^£ i     J

где элементы матриц F и H находятся из уравнений fp (x, y) = hJO®s (с p + [c p+1 - с p ]y)x au *((x, y), с p + [с p+i - с p ]y) x----------------— d у +

1          dn

+hJ0®s (с p-1 + [C p - с p-i]Y)x au*((x, y), с p-i + [с p - с p-i]Y) x-------------------------- dn hp(x,y) = - hJ0®s (сp + [cp+i -сp]y)x xu*((x,y),сp + [сp+i -сp]Y)dY-

-hJ0 ®p (с p-i + [c p - с p-i]Y)x xu*((x,y)сp-i + [сp -сp-i]Y)dY,

p = 1, ..., M .

Число коэффициентов в матрице T в системе уравнений (31) с учетом трехдиагональности матрицы A составляет N 1 N 2 (12 N 1 + 10 N 2 ) + 16( N 1 + N 2 )², где N 1 , N 2 – число узлов разбиения прямоугольной области Q по каждой стороне прямоугольника. Количество операций, требуемых для решения системы (31), можно оценить как О ( N 1 ² N 2 (12 N 1 + 10 N 2 )).

С помощью объединенного метода МКЭГ-МГЭ, представленного системой линейных уравнений (30), (31), производится расчет рассеянного поля как вдоль границы, так и во всех внутренних узлах. Для определения рассеянного поля во внешних по отношению к объекту точках, величины поля в граничных узлах линейно интерполируются, используя равенства (12), частные производные поля в граничных узлах линейно интерполируются, используя равенство (13), и интерполированные данные подставляются в уравнение (23), но ξ уже является внешней точкой, и функция c(ξ)=1.

Полное поле представляет собой сумму рассеянного и падающего полей [29]:

Jd u s          d u * I

^u ( x , y ) = ^u ( x , y )-Ф1 „ ^{u - u} —^ d Г ,

Г [ d n          d n(33)

( x , y ) g Q .

Для ТМ поляризации уравнение (33) в матричной записи имеет вид:

u=u in +Wu sc + 1      I Hv in =u ^,n + WT -

I ^£ i J

Численные примеры

Рассмотрим дифракцию плоской ТЕ-поляризованной волны на диэлектрическом однородном цилиндре с круглым сечением. Пусть плоская

волна падает на цилиндр слева направо вдоль оси x , длина волны Л о =i мкм. Относительная диэлектрическая проницаемость цилиндра ε=2, радиус равен 0,5 мкм. Окружающее цилиндр однородное пространство имеет параметры s = ^ =i. Расчет производился объединенным методом МКЭГ-МГЭ [26-28]. В качестве области Q выбиралась квадратная область размером Lxi мкм, а контура s - периметр области Q . После

нахождения проекции на ось z электрического вектора E z внутри области Q и на ее периметре s , рассчитывалось поле вне области Q в области V с помощью теоремы Грина по формуле (33).

На рис. 1 представлена зависимость от числа точек разбиения Q средних квадратичных отклонений сформированного поля от поля, рассчитанного аналитически [28], по интенсивности и амплитуде. В суммах из функции Бесселя и Ханкеля, аппроксимирующих комплексную амплитуду, учитывалось 30

слагаемых, что давало погрешность порядка 0,001 %. Средние квадратичные отклонения по ин-

тенсивности и амплитуде вычисляются соответст-

венно по формулам:

5 1 =

N ₂

X | I ( x_k , y , ) - I n ( X k , y , ) k , l =i ________________________________________________

N ₂

E [ i^M c ( X k , y , ) ]

k , l =i

I I x Uu in + l---- ¹ I Hv in ,

I ^£ i J

5 A =

N ₂

X l^u( x k , y , )l^- l^{u inc (} x k , y , )l k , I =i

N ₂

X [ U nc ( X k , y , ) ] k , , =i

где матрица W имеет следующий вид:

W =

⁰ [ F ] 7 [ H ]

£ ₁

Ошибка при уменьшении расстояния между узлами h , равного отношению размера области расчета l к числу узлов дискретизации N , до 0,03λ быст-

ро спадает и далее медленно уменьшается.

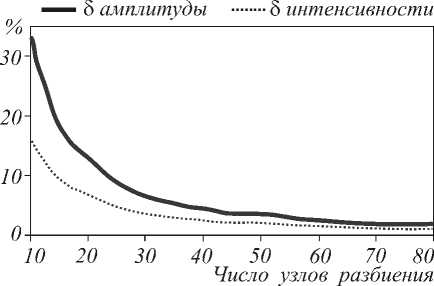
Рис. 1. Зависимость среднего квадратичного отклонения амплитуды и интенсивности рассчитанного поля (от аналитически рассчитанного поля) от дискретизации сетки

У противоположного падению волны края цилиндра наблюдается фокусировка поля, максимум которого лежит на границе раздела сред. На рис.2 приведена зависимость значений максимума интенсивности в зависимости от числа узлов дискретизации. Из графика видно, что значения максимума с увеличением числа узлов дискретизации стремятся к значению максимума, рассчитанному аналитически.

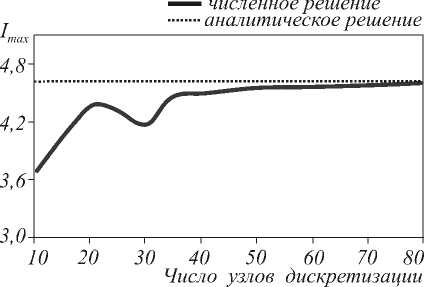
Рис. 2. Зависимость максимума интенсивности рассчитанного поля от дискретизации сетки

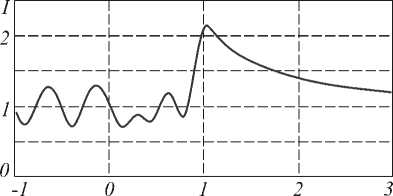
Распределение амплитуды поля дифракции на рассчитываемом диэлектрическом цилиндре показано на рис. 3. Число точек разбиения области Ω было равно N =50x50. Распределение амплитуды по оси х , проходящей через центр цилиндра, показано на рис. 4. Цилиндр располагается на координатах от 0 мкм до 1 мкм.

Ниже для сравнения приводятся результаты расчетов для ТЕ- и ТМ-поляризаций.

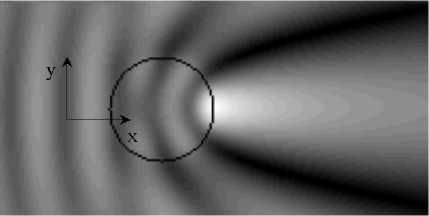
Рис. 3. Распределение амплитуды поля дифракции плоской ТЕ-поляризованной волны на круговой цилиндр, полученное объединенным методом

Л", л/юи

Рис. 4. Распределение амплитуды по оси х для рис. 3

Расчет поля дифракции ТЕ-поляризованной волны на диэлектрическом цилиндре с квадратным сечением 1х1 мкм и относительной диэлектрической проницаемостью ε =2 представлен на рис. 5. Число точек разбиения области Ω равно N =50x50. Распределение амплитуды по оси х , проходящей через центр, показано на рис. 6. Цилиндр располагается от 0 мкм до 1 мкм.

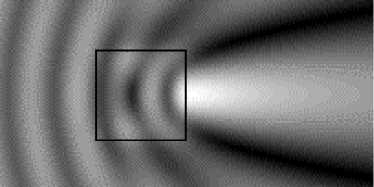
Рис. 5. Распределение амплитуды поля дифракции плоской ТЕ-поляризованной волны на квадратном цилиндре, полученное объединенным методом

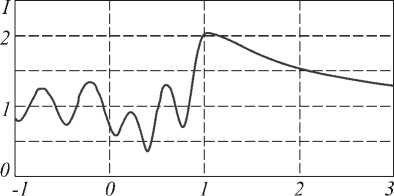
X, мкм

Рис. 6. Распределение амплитуды по оси х для рис. 5

Картины распределения амплитуды поля для цилиндров с круглым и квадратным сечением можно признать схожими. Хотя максимальное значение амплитуды поля наблюдается в случае круглого сечения.

Рассмотрим дифракцию плоской ТМ-поляризо-ванной волны на диэлектрическом однородном цилиндре с круглым сечением. Пусть плоская волна падает на цилиндр слева направо вдоль оси x, длина волны λ0 = 1 мкм. Относительная диэлектрическая проницаемость цилиндра ε=2, радиус равен 0,5 мкм. Окружающее цилиндр однородное пространство имеет параметры ε=µ=1. Расчет производился объединенным методом МКЭГ-МГЭ по формулам (32). В качестве области Ω выбирался круг радиусом 1 мкм, а контура S – периметр области Ω. Число точек разбиения на 1 мкм бралось 50. После нахождения проекции на ось z магнитного вектора Hz внутри области Ω и на ее периметре S, рассчитывалось поле вне области Ω в области Ψ с помощью теоремы Грина по формулам (33). Распределение амплитуды показано на рис. 7. На рис. 8 показано распределение амплитуды вдоль оси х. Начало координат находится на левом крае цилиндра. Рассчитанное распределение амплитуды совпадает с аналитическим решением с ошибкой по амплитуде δ =2%.

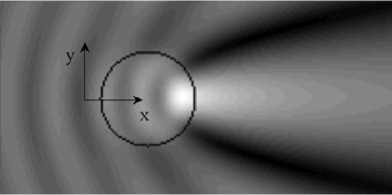
Рис. 7. Распределение амплитуды светового поля при дифракции плоской волны ТМ–поляризации

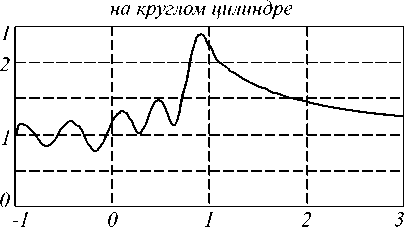
X, мкм

Рис. 8. Распределение амплитуды по оси х для рис. 7

Рис. 9. Распределение амплитуды поля дифракции плоской ТМ-поляризованной волны на квадратном цилиндре, полученное объединенным методом

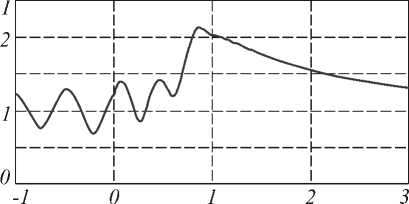
X, МКМ

Рис. 10. Распределение амплитуды по оси х для рис. 9

Расчет поля дифракции ТМ поляризованной волны на диэлектрическом цилиндре с квадратным сечением 1х1 мкм и относительной диэлектрической проницаемостью ε=2 представлен на рис. 9. Число точек разбиения области Ω равно N =50x50. Распределение амплитуды по оси х , проходящей через центр, показано на рис. 10. Цилиндр располагается от 0 мкм до 1 мкм.

Картины распределения амплитуды поля для цилиндров с круглым и квадратным сечением отличаются по характеру отраженной волны. В случае квадратного сечения рассеяние назад меньше, что можно объяснить влиянием кривизны границы среды. Максимальное значение амплитуды поля также наблюдается в случае круглого сечения. Можно заметить, при ТМ-поляризации максимум интенсивности находится уже не на границе раздела сред, как в случае ТЕ-поляризации, а внутри цилиндра.

Заключение

В работе полученные следующие результаты.

Разработан объединенный метод конечных элементов Галеркина и граничных элементов, с помощью которого можно моделировать дифракцию плоской электромагнитной волны ТМ-поляризации на однородных (и неоднородных) двумерных (цилиндрических) диэлектрических объектах микрооптики, размер которых сравним с длиной волны света.

Работоспособность метода продемонстрирована хорошим согласием (1-2%) полей дифракции плоской волны на круглом цилиндре, рассчитанных данным методом и по известным аналитическим формулам.