Объемная магнитострикция сплавов Fe-Ga: расчет из первых принципов

Сплавы Fe-Ga являются широко исследуемыми, перспективными магнитострикционными материалами, актуальными в технике в качестве датчиков микроэлектромеханических систем и преобразователей энергии. Небольшая добавка Ga в структуру α-Fe приводит к десятикратному увеличению магнитострикции сплавов относительно чистого железа [1, 2]. На магнитострикционные свойства сплавов существенное влияние оказывает фазовый состав композиций, который в свою очередь зависит от термических условий обработки образцов [2–6]. В медленно охлажденных образцах величина тетрагональной магнитострикции λ 100 в слабом магнитном поле достигает двух пиков: 180·10^–6 при x ≈ 19 ат. % и 156·10^-6 при x ≈ 27 ат. %. В закаленных образцах эти значения выше и составляют ~263·10^–6 вблизи 19 % Ga и 233·10^–6 около 27 % Ga [2]. Величина ромбоэдрической магнитострикции λ 111 составляет 25,3·10^–6 и 32·10^-6 в сплавах Fe 79,1 Ga 20,9 и Fe 71,2 Ga 28,8 , соответственно. Добавка немагнитных атомов Ga к железу влияет не только на величину линейной, но и объемной магнитострикции ∆ V/V . В работах [7, 8] показано, что в сильном магнитном поле в as-cast сплавах Fe₈₁Ga₁₉ объемная магнитострикция достигает значения 20·10^–6, что в пять раз больше относительно чистого Fe [7]. В поликристаллических сплавах с содержанием 15, 20 и 29 ат. % Ga в сильных полях (до 5 Тл) вклад объемной магнитострикции составил около 33 % [7, 8]. Авторы статей [7, 8] связывают полученные результаты с наличием полностью неупорядоченной структуры A2 в исследуемых образцах.

В рамках первопринципных вычислений постоянные магнитострикции λ 100 и λ 111 кристаллов кубической симметрии можно рассчитать исходя из зависимости энергии магнитокристаллической анизотропии E MKA от небольших деформаций [6, 9]. Для определения тетрагональной магнитострикции энергия системы вычисляется в направлениях [001] и [111], в случае ромбоэдрической – вдоль осей [111] и [ 112 ]. Разность энергий, полученных вдоль указанных направлений

Физика

позволяет определить энергию магнитокристаллической анизотропии, а затем и постоянные магнитострикции согласно формулам

₌ 3   dE MKA / ds ₌ _ b i .    _ ³   dE MKA / ds ₌    Ь 2

2V d2 E J ds2    3C111  2Vd2 EJ ds2    3C44’ полн                                    полн где V – объем структуры, C’, C44 – упругие константы, ε – малые искажения при постоянном объеме, Eполн – полная энергия. Результаты расчетов магнитострикции хорошо согласуются с экспериментальными данными и представлены в работах [6, 9–11]. В отличие от констант линейной магнитострикции, величину объемной магнитострикции можно оценить из зависимости энергии обменного взаимодействия от расстояния между парами спинов [12].

Целью данной работы является вычисление объемной магнитострикции сплавов Fe 100- x Ga x ( x = 18 – 22 ат.%) в структурных фазах A2 и D0 3 в зависимости от концентрации атомов Ga методом теории функционала плотности.

1.    Детали вычислений

Расчеты выполнены с использованием теории функционала плотности, реализованной в пакете SPR-KKR ( a spin-polarized relativistic Korringa–Kohn–Rostoker code ) [13]. Учет обменнокорреляционных эффектов проводился в приближении обобщенного градиента (general gradient approximations – GGA) в формулировке Пердью, Бурке и Эрнцернхофа (Perdew, Burke, Ernzerhof – PBE) [14]. Самосогласованные вычисления выполнены с использованием k -сетки 45³ с 2880 k -точками. Для опт и мизации кристаллической структуры были использова н ы две кубические структуры: A2 ( Im 3 m , группа симметрии № 229, прототип a-Fe) и D0₃ ( Fm 3 m , группа симметрии № 225, прототип BiF 3 ). Химический беспорядок моделировался с использованием приближения когерентного потенциала. Равновесные параметры решетки a 0 и объемный модуль упругости B были получены из зависимости полной энергии от объема ячейки в соответствии с уравнением состояния Берча–Мурнагана. Для каждой композиции Fe 100– x Ga x ( x = 18 – 22 ат. %) были вычислены константы магнитного обменного взаимодействия в гамильтониане Гейзенберга в зависимости от параметра решетки. Расчеты проводились на k -сетке 57³ с 4495 k точками. Объемная магнитострикция определялась по следующей формуле [12, 15]

A V _ r ₀ nz ^d J V ~ 3 B d r

B 0

(s i - ^S 11 = B •

где n – количество атомов, приходящихся на объем элементарной ячейки, Jij – обменный интеграл между атомами i и j, расположенных на наименьшем расстоянии r, z – число ближайших соседей, r0 - расстояние между атомами i и j для немагнитного состояния системы, Si(j) - спин единичной длины (| Si | = 1), Во - объемная магнитоупругая постоянная.

2.    Результаты вычислений

На первом этапе были проведены самосогласованные расчеты для структур A2 и D0₃ сплавов Fe_{100– x} Ga _x ( x = 18–22 ат. %) при различных параметрах решетки. Основываясь на полученных данных для различных концентраций х были вычислены константы магнитного обменного взаимодействия J_i j . Наибольшие взаимодействия в A2 и D0₃ структурах наблюдаются между атомами железа, расположенными в первой координационной сфере ( r^A2 = а л/3/2, r ^D0 3 = a Vs/4). В случае фазы A2 имеется один сорт атомов Fe, в то время как в кристаллической решетке D0₃ в зависимости от занимаемой позиции можно выделить три типа атомов: Fe 1 – занимающие позиции 8 c (¼, ¼, ¼); Fe 2 – размещенные на позиции 4 b (½, ½, ½); Fe 3 – расположенные на позициях 4 a (0, 0, 0) совместно с атомами Ga. Наибольшее значение констант J ^D °³ наблюдается между атомами Fe 1 –Fe 2 .

На рис. 1 представлены концентрационные зависимости констант магнитного обменного взаимодействия атомов железа в первой координационной сфере. Видно, что с увеличением параметра решетки обменное взаимодействие уменьшается в обеих структурах, что объясняется увеличением расстояния между ближайшими спинами. В неупорядоченной фазе A2 значения J ij больше, чем в фазе D0₃. При увеличении концентрации Ga в структуре А2 происходит усиление

Матюнина М.В., Бучельников В.Д., Загребин М.А., Соколовский В.В.

ферромагнитного взаимодействия между атомами Fe. Данный факт можно объяснить тем, что в неупорядоченной фазе А2 увеличение количества атомов Ga приводит к сближению атомов железа из-за большего радиуса атомов Ga и их случайного расположения в решетке. В упорядоченной D03 фазе, напротив, ферромагнитное взаимодействие Fe1–Fe2 ослабляется по мере увеличения атомов Ga в решетке из-за того, что они вынуждены размещаться по узлам упорядоченной кристаллической структуры, тем самым, увеличивая расстояние между ближайшими атомами железа.

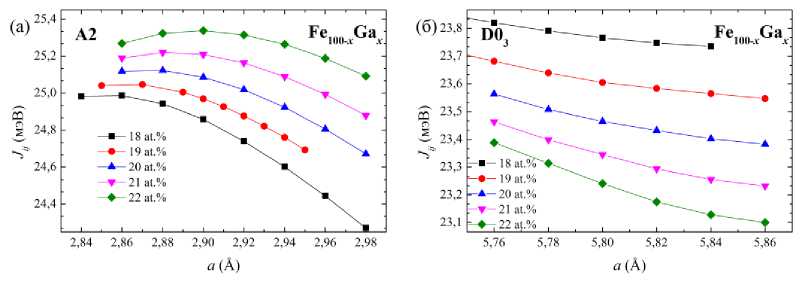
Рис. 1. Концентрационные зависимости констант магнитного обменного взаимодействия J ij от параметра кристаллической решетки a в первой координационной сфере для (а) A2 и (б) D0 3 фаз сплавов Fe 100– x Ga x

В соответствии с соотношением (1) рассчитаны объемные магнитоупругие постоянные, значения которых представлены в таблице. В таблице также приведены равновесные значения параметров решетки a0 и объемные модули упругости B. В исследуемом диапазоне концентраций 18 ≤ x ≤ 22 ат. % значение равновесного параметра практически не меняется с увеличением концентрации Ga и составляет a0 ≈ 2,92 Å для полностью разупорядоченной структуры A2 и a0/2 ≈ 2,90 Å для упорядоченной фазы D03. Добавка галия в решетку A2 приводит к уменьшению значений объемного модуля упругости B, в то время как в D03 фазе данный параметр практически не изменяется. Значения объемной магнитоупругой постоянной B0 отрицательны. По абсолютной величине значения B0A2 уменьшаются почти в два раза для композиции Fe78Ga22 по сравнению с составом Fe82Ga18. Для D03 наблюдается обратная зависимость поведения B0 (x) в ис- следуемом диапазоне.

Таблица

Равновесный параметр решетки a 0 (Å), объемный модуль упругости B (ГПа) и объемная магнитоупругая постоянная B 0 (ГПа) кристаллических структур A2 и D0 3 сплавов Fe 100– x Ga x

x , ат.%	A2			D0 3
	a 0	B	B 0	a 0 /2	B	B 0
18	2,915	171,0	–0,663	2,902	158,2	–0,060
19	2,917	158,7	–0,508	2,903	157,9	–0,063
20	2,919	166,5	–0,445	2,903	157,7	–0,088
21	2,923	164,1	–0,337	2,904	157,8	–0,115
22	2,924	163,5	–0,300	2,905	158,0	–0,145

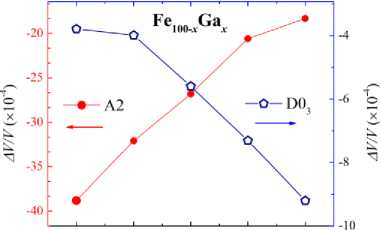
На основании данных таблицы получены значения объемной магнитострикции ∆ V/V в зависимости от концентрации Ga, показанные на рис. 2.

Как следует из таблицы и рис. 2, поведение зависимости ∆ V/V ( x ) повторяет зависимость B 0 ( x ). Порядок значений магнитострикции составляет 10^-3, что в сто раз больше экспериментальных данных, представленных в работах [7, 8]. В работе [8] значения ∆ V/V, полученные для поликристаллов с содержанием x = 15, 20, 29 ат. % в магнитных полях до 5 Тл составляют 15·10^–6, 29·10^–6 и 27·10^–6 соответственно. В as-cast сплавах Fe 81 Ga 19 объемная магнитострикция достигает значения 20·10^–6 [7]. Различие между экспериментальными данными [7, 8] и полученными в данной работе результатами может быть объяснено тем, что измерения магнитострикции в работах [7, 8] проводились при комнатной температуре, а расчеты выполнены при 0 К. В работе [15] значение ∆ V/V для Ni при температурах, близких к 0 K, составляет порядка –12·10^–4; при увеличении температуры постоянная объемной магнитострикции уменьшается. Согласно данным, по-

Физика

лученным в работе [16], объемная магнитострикция для сплавов Ni-Mn-Ga при комнатной температуре составляет –198·10–4. Таким образом, рассчитанные в данной работе значения объемной магнитострикции для сплавов Fe-Ga, согласуются с результатами, полученными для других соединений.

IS I')        20        21         22

Ga (jr, ат.%)

Рис. 2. Концентрационные зависимости объемной магнитострикции кристаллических структур A2 (левая ось) и D0 3 (правая ось) сплавов Fe 100– x Ga x

Заключение

В данной работе из первых принципов проведено исследование зависимости объемной магнитострикции от концентрации Ga в сплавах Fe_100–xGa _x ( x = 18 – 22 ат. %). Рассмотрены две кристаллические структуры кубической симметрии A2 и D0₃, наблюдаемые экспериментально в указанном диапазоне концентраций. При температуре 0 К рассчитаны параметры обменного взаимодействия в зависимости от параметра решеток. Из них определена объемная магнитоупругая постоянная. Показано, что величина констант магнитного обменного взаимодействия J_i j и объемной магнитоупругой постоянной B ₀ возрастает с содержанием Ga для структуры A2 и уменьшается для структуры D0₃. Получена композиционная зависимость объемной магнитострикции ∆ V/V . Показано, что теоретические значения объемной магнитострикции по абсолютной величине на два порядка выше, чем экспериментально измеренные в поликристаллических образцах в сильном магнитном поле. Различие между экспериментальными данными и полученными в данной работе результатами может быть объяснено тем, что измерения магнитострикции проводились при комнатной температуре, а расчеты выполнены при 0 К. Значения объемной магнитострикции для сплавов Fe-Ga согласуются с результатами для других соединений.

Работа выполнена при поддержке гранта № 17-72-20022 Российского Научного Фонда (разделы 1 и 2), М. Загребин выражает благодарность Фонду поддержки молодых ученых Челябинского государственного университета.