Области сопротивления для модели однокоренного зуба: различные случаи симметрии

Центр сопротивления рассматривается как наиболее важный ориентир при планировании краткосрочных и долгосрочных перемещений зубов. Это обусловлено тем, что сила, линия действия которой проходит через эту точку, приводит к поступательному движению зуба. Другие виды движения зубов, как правило, также описываются с учетом расположения центра сопротивления или кривых момент / сила [3, 4, 8, 10, 14, 15, 17].

История развития понятия «центр сопротивления», а также различные подходы к его определению представлены в фундаментальной работе [7]. Один из выводов авторов указывает на необходимость пересмотра этого понятия с учетом результатов последних исследований. К таким исследованиям, в частности, можно отнести работы [18, 20], посвященные численным экспериментам для асимметричной периодонтальной связки верхнечелюстного первого моляра. Результаты этих работ показали, что не существует единого центра сопротивления (центр сопротивления не является точкой в трехмерном пространстве) применительно к неидеализированному (асимметричному) корню зуба и периодонтальной связке. При планировании движения любого зуба предложено использовать трехмерные оси сопротивления, которые не пересекаются в одной точке [20]. Для клинических целей предлагается использовать малый трехмерный объем, ограниченный осями сопротивления, как объем, содержащий центры сопротивления, соответствующие поступательному перемещению зуба в различных направлениях. Аналогичный подход, основанный на использовании понятия радиуса сопротивления, предложен в работе [5]. Более строгий подход к определению условий поступательного перемещения корня зуба в периодонтальной связке, основанный на понятиях области сопротивления и прямых поступательного воздействия, предложен в работе [11]. Это определение получило развитие и обобщение в работе [6] для области сопротивления как конечного или бесконечного множества точек. В работах [6, 11] показано, что зуб получает поступательное перемещение (необязательно в направлении действия силы) в случае, если линия действия нагрузки проходит через точку области сопротивления и направлена соответствующим образом. Такая линия действия является прямой поступательного воздействия [6, 11]. Также в работах [6, 11] показано, что область сопротивления может быть эллипсом (общий случай), двумя точками или одной точкой (исключительные случаи). Настоящее исследование развивает это актуальное направление для корней однокоренных зубов в форме составного параболоида. Целью работы является математическое моделирование области сопротивления для симметричных и асимметричных корней зубов.

Равновесие корня зуба в периодонтальной оболочке

При математическом моделировании напряженно-деформированного состояния системы «зуб – периодонтальная связка» в большинстве случаев корень зуба аппроксимируется абсолютно твердым телом в форме параболоида или гиперболоида [2, 12, 16]. Как показали результаты исследования [21], реальная форма однокоренного зуба с достаточно высокой точностью может быть аппроксимирована с помощью параболоида. Исходя из этого будем считать, что внешняя поверхность корня зуба (совпадающая с внутренней поверхностью периодонтальной связки) и внешняя поверхность периодонтальной связки, прилегающая к костной ткани зубной альвеолы (смещенная по нормали по отношению к поверхности корня зуба на величину 5 ), описываются уравнениями параболоидов:

Fk (x, y, z ) = y - h ((xlak )2+(zb )2 ) = 0

F ⁽ k ) ( x, y , z ) = y + n yk ) 5- h

где h - высота корня зуба; а_к , b_k - полуоси эллипса в сечении корня зуба на уровне альвеолярного гребня, а ₄ = а , =  .      , а ₃ = а ₂ =   .  ²   , b ₂ = b , b ₄ = b ₃, e_x , e_n   -

-e^

( k )       ( k )       ( k )

эксцентриситеты эллипсов; n^v_x ⁷, n ⁷, n - компоненты единичного вектора нормали к к -й поверхности корня зуба (1), к = 1,4; поверхности F_k ( x , y , z ) и F ( ^к ) ( x , y , z ) при к = 1 определены на промежутках x >  0, y >  0, при к = 2 на x <  0, y >  0, при к = 3 на x <  0, y <  0 и при к = 4 на x >  0, y <  0.

При действии на зуб сосредоточенной силы f = ( f , f , f ) точки периодонта, прилегающие к поверхности корня зуба, получают перемещения, равные перемещению корня. Внешняя поверхность периодонтальной связки (2) является жестко закрепленной. Будем предполагать, что нагрузка сохраняется достаточно низкой, чтобы обеспечивать деформации периодонтальной связки, соответствующие начальному линейному участку диаграммы напряжения – деформации. В этом случае ткани периодонтальной связки с достаточно высокой точностью можно считать линейно упругим материалом [9, 19, 20]. Также в соответствии с работами [12, 13, 16] будем считать периодонт несжимаемым материалом с коэффициентом Пуассона равным 0,49. С учетом этого компоненты тензора деформаций в системе координат, связанной с нормалью, образующей и направляющей к внешней поверхности корня зуба, можно определить следующим образом [12]:

^£ nn = ^- u n /⁵ , ^£ tt = ^£ ее = ⁰, Y n e = ^- u е/ ⁵ , Y nt = ^- U /⁵ , Y t е = ⁰,              (3)

где un, ut, u6 - перемещения точек периодонта вдоль нормали, образующей и направляющей к поверхности корня зуба; 5 - ширина периодонтальной связки в направлении нормали к поверхности (1). Нормаль n , образующая t и направляющая е

к поверхности корня зуба, а также его геометрические размеры показаны на рис. 1.

После преобразований уравнений равновесия корня зуба, описанных в работах [1, 16], получим систему однородных алгебраических уравнений относительно малых

поступательных перемещений е = (О, еу, О) следующего вида:

^U 0 = ( ^U 0 x , ^U 0 y , ^U 0 z ) и

углов

поворота корня зуба

"A lr T

											X
	' a 11	a 12	а„		а 44	a 45	а 46		1 а ' 4	a 15	а ' 6
А =	a 21	a 22	a 23	, В =	a 54	a 55	a 56	, Г =	a 24	a 25	a 26
	( а31	a 32	а 33 J		( a 64	a 65	а 66 J		( а 34	a 35	а 36 J

Здесь ay = a^  - коэффициенты, зависящие от физико-механических свойств и геометрических размеров периодонтальной связки; m = ( mx, my, mz ) = r x f - главный момент внешних сил; f = (f, f, f) - главный вектор внешних сил; r = (xy, yf, zf)

-

радиус-вектор; x_f , y^ и z_f - координаты точки приложения нагрузки. Выражения для коэффициентов a приведены в приложении.

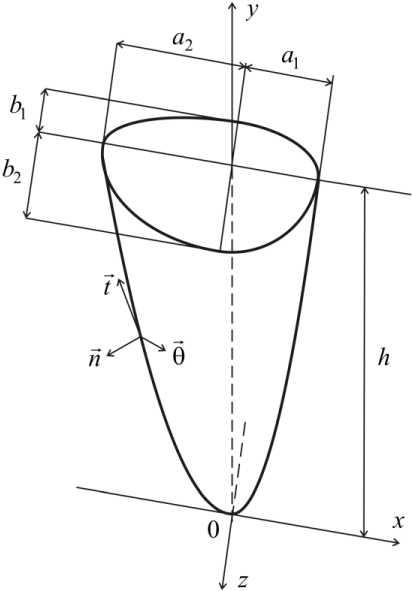
( x , y , z )

и

( n , t , б ) и

Рис. 1. Системы координат

геометрические размеры

асимметричного корня зуба, состоящего из четырех различных параболоидов

Решение системы (4) представим в матричном виде, предложенном в работе [11]:

(77 Л   fa

711 f

u 0      a

^Дт ^t

T где y - транспонированная матрица y .

Различные случаи симметрии

Модель корня зуба в форме параболоида с круговым сечением

Для корня зуба в форме кругового параболоида имеем b = a_x = a ₂ = b = b .

С учетом ненулевых коэффициентов системы (4) матрицы системы (5) принимают вид

'*" 0 0 1 Г k44 0 0 1 г 0 0 —k34 a = 0 22 0 , e= 0 k55 0 , 7 = 0 0 0 v 0 0 kll, v 0 0 k44 v v k34 0 0 a44                1                a11                1                a34

' 11                     2 , ^22            , ^44                     2 ,    55            ,    34                     2 ^.

a ll a 44 — ^a34          a 22          a ll a 44 — a 34          a 55          a ll a 44 — a 34

Матрица 5 , являющаяся симметричной частью матрицы уР ¹, представляет собой нулевую матрицу. Согласно [6, 11] в этом случае существует единый центр сопротивления корня зуба, координаты центра сопротивления определяются матрицей е (антисимметричной частью матрицы ур^{— 1}). Зуб принадлежит к типу ( 0,0,0 ) по классификации [11]. Соответствующее преобразование матриц (6) показывает, что координаты центра сопротивления равны ( 0,0, a₃₄/a ₁ J. Любая сила, линия действия которой проходит через эту точку, приводит к поступательному перемещению зуба.

В табл. 1 приведены значения ненулевых коэффициентов a . Радиус сечения корня на уровне альвеолярного гребня b = 3,9 мм, высота корня h = 13,0 мм; упругие свойства периодонтальной связки описываются константами E = 680 кПа, v = 0,49 [12, 15, 16], толщина периодонтальной связки 5 = 0,229 мм [12, 16].

С учетом данных табл. 1 координаты центра сопротивления равны ( 0;0; 8,431 ) мм.

Модель корня зуба в форме параболоида с эллиптическим сечением

В этом случае с коэффициентами

a , i , j = 1, 6, при a = a_x = a₂ и b = b = b₂

получаем следующие матрицы:

a =

^k 11 =

^k 55

I ⁰

a ₆₆

^a 11 ^a 66    ^a 16

, ^k 66 a ₅₅

0 )       ( к 44

0  , Р= 0

k ₃₃

I ⁰

, ^22           , ^33

a ₂₂

a ₁₁

2 ^a11 a 66   ^a 16

0 k ₅₅ 0

a ₄₄

a ₃₃ a ₄₄

—

2   , ^k 44

a ₃₄

00 ,

a ₃₃

a ₃₃ a ₄₄

—

2 , a ₃₄

^a 34                      ^a 16

'34                    2 , k16                       2 ■ a33 a 44 — a34           a11 a66 — a16

Матрица 5 является ненулевой и имеет вид

5= 0

r

0 г r13

0  0

0  0 J

_ _ ^a 16 ^a33 + ^a11 ^a 34 r 13          ~

2 a ₁₁ a ₃₃

Собственные числа и векторы этой матрицы

• 5 1,2 = r 3 , 5 э = 0, v = (VV 2,0,VV2 ) , V 2 = ( — VV2,0,VV2 ) , V 3 = ( 0, — 1,0 ) ■

Таким образом, корень зуба в форме эллиптического параболоида принадлежит к типу ( + , — , 0 ) по классификации [11]. Прямые поступательного воздействия расположены в плоскостях x = 0 и z = 0. Область сопротивления образуют точки р и P с координатами (0,0, — a.Ja. J и (0,0, a₃₄/a ₃₃) соответственно. Если линия действия силы расположена в плоскости x 0 y (или z 0 y ) и проходит через точку P (или P ), то зуб получает поступательное перемещение в плоскости x 0 y (или z 0 y ).

Таблица 1

Коэффициенты a _ij для модели корня зуба с круговым сечением

au = a 33, МН/м	a 22, МН/м	a 44 = a 66 , Н	a 55 , Н	a 16 =- a 34 , кН
5,363	0,833	443,031	1,967	–45,214

Таблица 2

Коэффициенты a _ij для модели корня зуба с эллиптическим сечением

a 11, МН/м	a 22, МН/м	a 33 , МН/м	a 44 , Н	a 55 , Н	a 66 , Н	a 16 , кН	a 34 , кН
5,043	1,090	6,997	578,901	6,137	445,565	–44,168	59,060

Значения коэффициентов системы (4) приведены в табл. 2. Малая полуось эллипса на уровне альвеолярного гребня b = 3,9 мм, a = .     , еп = 0,6 . Остальные et1

геометрические размеры корня зуба и постоянные упругости периодонтальной связки имеют прежние значения.

В соответствии с данными таблицы координаты точек P и P , образующих область сопротивления, равны (0; 0; 8,759) мм и (0; 0; 8,441) мм соответственно.

Модель корня зуба в форме составного параболоида с одной симметрии плоскостью

различными имеет одну

Для корня зуба, поверхность которого описывается двумя параболоидами, будем считать b = b = b2. В этом случае корень зуба плоскость симметрии z = 0. Матрицы системы (6) записываются следующим образом:

а =

f k» ^k 12

. 0

^k 12

If

^k11    k а ( a 26   a 22 a 66

0 '		Г 0	0	k 16
0	, Y =	0	0	k 26
k 66 ,		4 k 34	k 35	0

) , ^k12   ^k а ( a 12 a 66    a 16 a 26 ) , k 22    ^k а ( a 16

- a ll a 66 ) ,

k33   ke( a45   a44a55 ) , k44   k|3 ( a35   a33 a55 ) , k55   k₽( a34   a33 a44 ) , k45   kp( a33a45   a34a35 ) , k66   ka( a^   au a22 ) , k16   ka( a16a22 a12a26 ) , k26   kа( a11 a26   a12a16 ) , k34   k₽( a34a55   a35 a45 ) , k35   k₽( a35 a44   a34 a45 ) , kа   a22 ( a16

-

a 11 a 66 ) + ^a 66 a 12    ² a 12 a 16 a 26 + a 11 a 26 ,

^k p    a 44 ( a 35

-

a 33 ^a 55 ) + a 34 a 55   ^{2 a} 34 a 35 a 45 + a 33 a 45 ^.

Матрица 5

принимает вид

5 =

" 0

^, r¹³    2

1   a 16 a 22

² a ₁₂

^a12 a 26    a 34

a ₁₁ a ₂₂      a ₃₃

,

Г ₃ = “

23    ₂

Л ( Л Л

1   a ₁₁ a ₂₆

² a ₁₂

^a12 ^a16   ^a35

a ₁₁ a ₂₂      a ₃₃

.

Собственные числа и векторы этой матрицы

⁵ 1,2 = +

r 23 , ⁵ 3    ⁰ , v 1,2

^r 13   _, ^r 23   _{, 1  , v}

5 1,2 , 5 1,2 , J 3

=

— Г 23 ,1,0 .

^Г 13        у

Отсюда следует, что корень зуба в форме составного параболоида с одной плоскостью симметрии, так же как и симметричный корень зуба с эллиптическим поперечным сечением, принадлежит к типу ( + , — , 0 ) по классификации [11].

Плоскости, в которых расположены прямые поступательного воздействия, определяются следующим уравнением:

z ( ( y ^— y 2 )( x

—

^x 3 ) ^—( У ^— У 1 )( x

—

Областью сопротивления являются две точки: р (x3,0, y ) и р (x2,0, y2) , a16a22

y 1       2

^a 12

—

a 12 a 26             a 35           a 34

,   x 2            ,    ^y 2          , x 3

a ₁₁ a ₂₂

a ₃₃

a 12 a 16

2 a ₁₂

—

^{a 11 a 26} . Прямые поступательного

^a11 a 22

воздействия, проходящие через точку р и расположенные в плоскости z = 0, приводят к поступательному перемещению в этой плоскости. Прямые поступательного воздействия, расположенные в плоскости ( y — y ₂)( x — x ₃) — ( y — у_г )( x — x ₂ ) = 0 и проходящие через точку P , приводят к поступательному движению в пространстве. Точки P и P находятся на прямой, по которой пересекаются эти две плоскости.

Ненулевые коэффициенты a приведены в табл. 3. При их вычислении bb etX = 0,6,  ez2 = 0,2. Остальные

принимаем b = 3,9 мм, a_x = ,     ,   a ₂ = .      ,

V^{1— e}t1        71^— e 2

геометрические размеры корня зуба и постоянные упругости периодонтальной связки имеют прежние значения.

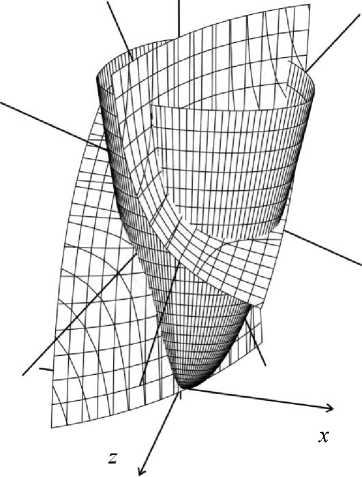
На рис. 2 показан корень зуба и плоскости, в которых расположены прямые поступательного воздействия (геометрические размеры корня зуба приведены выше, координаты точек P и P определены в соответствии с данными табл. 3).

Прямая AB (рис. 2, б ) является линией пересечения двух плоскостей, содержащих прямые поступательного воздействия. Через точку P в плоскости 1 проходят линии действия сил для поступательного перемещения в плоскости x 0 y , через точку P в плоскости 2 проходят линии действия сил для поступательного перемещения в пространстве. Точки P и P принадлежат прямой AB и имеют координаты ( 0,234; 0; 8,600 ) и ( 0,303; 0; 8,438 ) соответственно (значения координат приведены в миллиметрах).

Таблица 3

Коэффициенты a _ij для модели корня зуба с одной плоскостью симметрии

a 11, МН/м	a 22 , МН/м	a 33, МН/м	a 44 , Н	a 55 , Н	a 66 , Н
5,189	0,972	6,247	516,525	4,093	444,265
a 12 , кН/м	a 16 , кН	a 26 , кН	a 34 , кН	a 35 , кН	a 45, Н - м
–92,470	–44,639	1,022	52,703	–1,890	–17,526

Модель корня зуба в форме асимметричного составного параболоида

Если поверхность корня зуба описывается уравнениями четырех различных параболоидов, то все коэффициенты a, , i , j = 1, 6 являются ненулевыми. Также отличны от нуля все компоненты матриц решения (5) и матриц 5 и £ . Чтобы избежать громоздких выкладок, нахождение области сопротивления для асимметричной модели корня зуба выполним численно. Высота корня зуба h = 13,0 мм, полуоси b = 3,9 мм, b ₂ = 2,0 мм, a_Y =   . ^1   , a ₂ =   .  ²   , e_tX = 0,6, e_n = 0,75 , постоянные упругости для

• V^{1 -} e i      V^{1 -} e 2

периодонтальной ткани имеют прежние значения. Значения коэффициентов a , i , j = 1,6 приведены в табл. 4.

Собственные числа и векторы матрицы 5 имеют вид

• 5 «- 261,80 - 10 - 6 , 5₂ « 104,461 - 10 - 6 , 5₃ * 153,038 - 10 ^{- 6},

v « ( - 0,630; - 0,584; 0,514 ) , v « ( 0,717; - 0,691; 0,093 ) , v « ( 0,301; 0,427; 0,853 ) .

Отсюда следует, что асимметричный корень зуба принадлежит к типу ( + , + , - ) по классификации [11]. Областью сопротивления в этом случае является горловой эллипс однополостного гиперболоида

Р 11 x ² + p 22 z ² + p 33 y ² + P 12 xz + P 13 xy + p 23 zy + P i x + p 2 z + p 3 y + p 0 = 0 .        (7)

Коэффициенты a _ij в случае асимметричного корня зуба

y

a

Рис. 3. Прямые поступательного воздействия ( a ), проходящие через горловой эллипс однополостного гиперболоида (8), и область сопротивления ( б ) для асимметричного корня зуба с прямыми поступательного воздействия (масштаб по координатным осям приведен в миллиметрах)

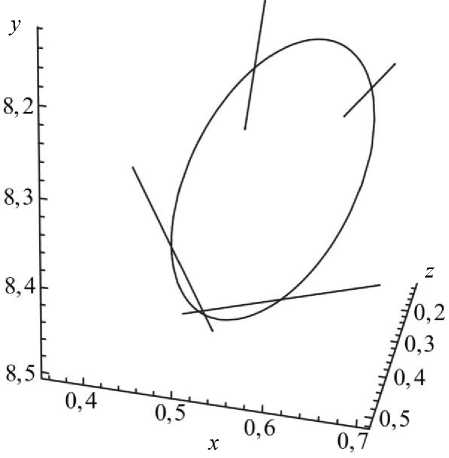
б

Таблица 4

a 11 , МН/м	a 22 , МН/м	a 33 , МН/м	a 12 , кН/м	a 23 , кН/м	a 13 , кН/м	a 34 , кН
3,849	0,629	5,832	–140,343	–273,895	97,168	47,783
a 44 , Н - м	Й 55 , Н - м	a 66 ,Н - м	a 45 , Н - м	a 46 , Н - м	a 56 ,Н - м	a 35 , кН
458,902	9,017	319,459	–33,957	–10,073	–16,324	–3,764
a 14, Н	a 15 , кН	a 16 , кН	a 24 , кН	a 25 , Н	a 26 , кН	a 36 , Н
877,467	1,781	–32,500	–2,346	109,886	1,462	–987,353

Таблица 5

Коэффициенты уравнения (7) однополостного гиперболоида

p 11	p 22	p 33	p 12	p 13	p 23	p 1	p 2	p 3	p 0
–2,117	1,126	0,401	33,338	–43,455	29,251	0,353	–0,262	0,008	–0,000087

Приближенные значения коэффициентов уравнения гиперболоида (7) приведены в табл. 5.

После приведения к каноническому виду уравнение (7) принимает вид z0 y0   x0

2 +   2      2    1 , az   ay

ax

где  aT * 0,126 мкм, a * 0,200 мкм, xy

a_z * 0,165 мкм. Координаты   ( x ₀, z ₀, y ₀)

выражаются через координаты ( x , z , y ) следующим образом:

x0 * -0,005 + 0,629x + 0,584y - 0,514z , y0 * -0,004 + 0,301x + 0,429y + 0,853z, z0 *-0,005 -0,717x + 0,691y-0,093z.

Образующие однополостного гиперболоида (7), проходящие через точки горлового эллипса, являются прямыми поступательного воздействия [6, 11]. На рис. 3 показаны корень зуба и область сопротивления (7), а также горловой эллипс с прямыми поступательного воздействия. Если линия действия нагрузки проходит вдоль прямой поступательного воздействия, зуб получает поступательное перемещение в пространстве.

Прямые поступательного воздействия, показанные на рис. 3, a и б , проходят через вершины горлового эллипса. Точки приложения нагрузок к корню зуба для его поступательного перемещения расположены на линиях пересечения однополостного гиперболоида и составного параболоида.

Заключение

• 1.    Области сопротивления для симметричных и асимметричных корней зубов, внешняя поверхность которых может быть описана одним уравнением параболоида, а также двумя или четырьмя уравнениями различных параболоидов соответствуют типам областей сопротивлений, определенных в работах [6, 11].

• 2.    Для корня зуба в форме параболоида с эллиптическим сечением, имеющим нулевой эксцентриситет, областью сопротивления является одна точка (единый центр сопротивления). Если эксцентриситет эллипса отличен от нуля, область сопротивления состоит из двух точек, расположенных на пересечении плоскостей симметрии, в которых лежат прямые поступательного воздействия. Расстояние между точками будет тем больше, чем больше эксцентриситет эллипса.

• 3.    Для корня зуба, состоящего из двух параболоидов с полуэллиптическим сечением и одной общей полуосью, одна из плоскостей, содержащих прямые поступательного воздействия, является плоскостью симметрии. Вторая плоскость с прямыми поступательного воздействия перпендикулярна этой плоскости, но располагается не вертикально. Эта плоскость у альвеолярного гребня наклонена в сторону полуэллипса с меньшим эксцентриситетом.

• 4.    Областью сопротивления асимметричного корня зуба, состоящего из четырех различных параболоидов, является горловой эллипс однополостного гиперболоида. Область сопротивления полностью расположена внутри корня. Прямолинейные образующие однополостного гиперболоида, проходящие через горловой эллипс, являются прямыми поступательного воздействия.

• 5.    Наибольшее расстояние между точками, ограничивающими область сопротивления для корня зуба в форме симметричного параболоида с эллиптическим сечением, составного параболоида с одной плоскостью симметрии и асимметричного составного параболоида, не превышает 0,3 мм. Для корней зубов указанной геометрической формы и корня зуба в форме кругового параболоида область сопротивления располагается на расстоянии, составляющем 64–65 % от длины корня зуба (если считать от вершины корня). С учетом малых размеров области сопротивления и ее приближенной локализации наиболее важным для оценки условий поступательного перемещения корня зуба представляется расположение прямых поступательного воздействия и координат точки приложения нагрузки.

Благодарности

Работа выполнена при поддержке программы научных исследований FP7 IRSES Marie Curie (грант № 610547 TAMER).

Приложение

Выражения для коэффициентов a_y ( E , v - модуль упругости и коэффициент Пуассона периодонтальной связки):

an=A Eff( n (k) (1 -2v)cos (a k)-(2 Hnk) (1 -v)+Gnk) (1 -2v)) sin (a k )^Fk, k=1 Fk a12 = a21 = A (1 - 2 v ) E fj (2vnXk) C0S (ak ) - Hkn(k) (1 - 2v) sin (ak 1^Fk , k=1 Fk ai3=a 31 =- A Eff( 2GvnXk)+Hk (1 -2v) nZk)) sin (a k) dFk, k =1 Fk aM = a4i =-AE ff^2vn(k)z cos (a) + (2Gkvn(k)y + 2GkH2vn(k)y +

14      41                        x                               x                      x k=1 Fk

+ H_k ( 1 - 2 v ) ( H 2 n ^{( k} ) y - n ^k ) z )) sin ( а Й dF_k , k            kz      y           k     k

a15 = a 51 = - AEff ((1 - 2v) n(k)Z cos (a k ) + ( Hk (nZk)X (1 - 2v) - 2 znXk) (1- v)) +

+Gk (2v( xn(k) + zn (k))-zn (k))) sin (a-)) dFk, a16

= a 61 = A E ff ( ( yn ( k ) ^{- 2 v} ( ^xnX^k ) ⁺ yn ^{( k} ) ) ) ^cos (^a k )^-

- (2 H_k ^k yn ( ^k ) (1 - v) + G_k ^k yn ( ^k ) (1 - 2v) + G_kH 2 yn ( ^k ) (1 - 2v) - k x           k z             kk z

-Hk (xnyk) (1- 2v)- 2G2УпХk) (1- v)))sin (ak ))dFk, a 22 = A Eff( 2 n (k ) (1 -v) COs (“ k )-(1 - 2v)( HknXk)+ GknZk)) sin (a k )^dFk , k=1 f a2k = a32 = AEff (nzk) (1 - 2v) COs (ak )- 2Gkvnkk) sin (ak )^Fk , k =1 Fk a24 = a42 = Aijj((ynzk)(1 - 2V)- 2znУк)(1 -V))cos (ak ) +

+(Hznk) (1-2v)-2 Gkynyk )v-Gk (2 Hkynyk )v -znzk) (1-2v)) sin (a k)) dFk, a 25 = a 2 = A Ll jj ((znxk) — xnk)) (1 — 2v) cos (a k ) + 2 n (k )v (Gkx - Hkz ) sin (a k )dFk ,

a26 = a62 = AL jj ((2xnyk) (1 - v) - ynXk) (1- 2v))cos (ak ) - k =1 f

a 33 = AL jj (n yk) (1- 2v)cos (a k)- (Hnk) (1- 2v)+2 GknZk) (1- v)) sin (a k ))dFk, k=1 Fk а 34 = a 43 = A Ljj(( yn yk) (1 - 2v)-2 zn k )v) cos (a k )-k =1 Fk

-(Hkynxk) (1- 2v)+ 2Gk3ynzk) (1- v)+ Gk (2Hkynzk) (1- v)- znyk) (1- 2v)))sin(ak))dFk, a 35   a 53