Обобщение метода Петрова-Галеркина для решения системы интегральных уравнений Фредгольма второго рода

Пастухов Ю.Ф. лицензируется под CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите

В работах [1], [2], [3] описана постановка задачи для интегрального уравнения Фредгольма второго рода и различные ее методы численного решения. Одним из важных методов является проекционный метод Петрова– Галеркина, применяемый для одного интегрального уравнения Фредгольма в конечномерных пространствах линейно-независимых координатных функций. Уравнение Фредгольма второго рода подробно изучено в работе [4], в частности, для малых значений λ и для больших значений параметра λ.

Однако при удачном выборе системы координатных функций применение проекционного метода Петрова–Галеркина не требует малости параметра λ (требуется проверка удаленности λ от всех собственных значений интегрального ядра [1], [2]).

В данной работе мы обобщили метод Петрова–Галеркина на систему интегральных уравнений Фредгольма. В последнее время уравнения Фредгольма второго рода активно применяются в конформных отображениях [5], в механике [6]. В работе [7] для численного решения уравнения Фредгольма с двойной точностью при небольших параметрах λ применен метод замены интеграла в матричной форме.

Постановка задачи

Рассмотрим систему линейных уравнений Фредгольма 2-го рода, которую будем решать проекционным методом Петрова– Галеркина. Метод решения одного интегрального уравнения Фредгольма (1) описан в работе [1], [2], [3].

b

• y ( x ) - 2 J K ( x , s ) y ( s ) ds = f ( x ) ,         (1)

a где: K(x,s) e C([a,b]x[a,b]) - непрерывная функция (кусочно-непрерывная на квадрате (x, s) e[a, b] x [a, b] - ядро интегрального уравнения Фредгольма (1)), f (x) e C[a, b] - заданная непрерывная правая часть уравнения (1), 2 - известный параметр. Обобщим уравнение (1) на случай m интегральных уравнений и m неизвестных квадратично-интегрируемых функций y, (x) e L2 [a, b], i = 1, m [1, 2]. Правые части уравнений f (x), i = 1, m и параметры 2i,j, i, j = 1, m в задаче (2) заданы. Число интегральных ядер Kt;(x,s) e C([a,b]x[a,b]),i,j = 1,m в системе интегральных уравнений (2) равно m2

.

m ^b

• У , ( x ) — X 2 J K i,j ( x , s ) y j ( s ) ds = f . ( x ), i , j = 1, m .   (2)

j = 1        a

Определение 1. Задачу (2), у которой интегральные ядра имеют только равные индексы i = j , назовем диагональной . Очевидно, что каждая неизвестная функция y ,. ( x ) в диагональной задаче входит только в свое i -е уравнение, а система интегральных уравнений разбивается на m независимых ур ав нений с разделенными функциями y_t ( x ), i = 1, m .

Например, явление квазиупругости в механике сводится к диагональной задаче из двух интегральных уравнений [8], в которой функции механического напряжения и относительной деформации связаны дополнительно линейным законом Гука.

Определение 2. Задачу (2), у которой интегральные ядра содержат произвольные индексы i <  j ( i >  j ) , назовем смешанной . Если при этом отсутствуют ядра K _;( x , s ) и параметры R, с равными индексами i = j , то задачу (2) назовем антидиагональной .

Сначала решим задачу (2) методом Петрова–Галеркина в общем виде. Затем в качестве частного случая рассмотрим анти-диагональную систему двух интегральных уравнений.

Как и в работе [1], выберем две системы линейно      независимых      функций

Ы^{x ) }} L, ^{ j , ^{( x ) }} n = i .

По первой системе координатных функций { ы ( x ) } ⁿ ₌₁ запишем разложение неизвестных функций решения y . ( x ), j = 1, m , для удобства добавляя каждый раз ф ункцию правой части системы (2) f ( x ), i = 1, m .

Решение системы уравнений (2) ищем в виде (3):

n

y ^{( x} ) = f ^{( x} ) + ^ C ^{Ы ( x}), i = 1, ^m , J = 1, n .   ⁽³⁾

j = i

Коэффициенты разложения C i , i = 1, m , j = 1, n в формуле (3) неизвестны ( n ■ m неизвестных). Подставим искомые функции y , ( x ) в систему интегральных уравнений (2):

n                mb f,(x)+£ СЫ(x)- £ 4, j Kj(x, s )l f(s)+£ Ck Ык(s) I ds=

J=1               j=1 a             к           к=1

n

= f i ^{( x} ) « R i ^{( x} ) = £ ^С Ы ^{( x} ) -

J = 1

mbn

• — £MKJx,s)\fj(s) + £СЫ(s)|ds, к = 1,n .(4)

J =1      a              к           к=1

В формуле (4) функция R ( x ), i = 1, m представляет собой невязку i -го уравнения в системе уравнений Фредгольма (2). П от ребуем ортогональности невязки R ( x ), i = 1, m всем функциям линейно-независимой второй системы:

J i ( ^x ) } ⁿ = 1 <  R i J i >= 0, i = 1, m, i = 1, n . (5)

Запишем формулу (5) - n ■ m условий более подробно с учетом формулы (4), в первой сумме заменим индекс j на k.

m

—

nb

£ Ск J Ык(x )Ji(x)dx— к=1

bb

£ R J J J ^{( x} ) K i , j ^{( x} , ^{s )} l f ^{( s} ) ⁺

n

£ С Ы ( s ) | dsdx = 0 о

j=1     а а                      к           к=1

£ Ск J Ык (xJ (x) dx—£ R £ Cj J J j (x)Kij (x, s Ы (s) dsdx = к=1 a m    bb

j = 1       ^к = 1      a a

= £ ^ j J J Jl (x)Ki, j (x, s) fj (s)dsdx, i, j = 1, m, к, l = 1, n .(6)

j = 1       a a

Введем в формуле (6) обозначения: b                       bb ак, i = J Ык (xJ (x) dx, j = J J Ji (x)Ki , (x, s Ы (s) dsdx a                       aa bb fj', l = J J J (x)K. J (x, s)f(s) dsdx, i, j = 1, m, к, l = 1, n .

aa

Тогда формула (6) примет вид n              j=m, к=n                 m                    ____ ____

£ с , , k a k,l — £ jj , к = £ j , ⁱ , i , j = 1, m ; к , i = 1, n .  (7)

к = 1                   j = 1, к = 1                       j = 1

В формуле (7) всего m ■ n условий для определения m ■ n элементов неизвестной матрицы коэффиц и ентов ра зл ожен и я. Коэффициенты a _k , _i ; к , i = 1, n , bj[ ; j , i = 1, m ; к , i = 1, n , f j , ⁱ найдены, а матрица параметров ^ ; i , j = 1, m задана в задаче (2). Система условий (7) содержит трехиндексные f ^{i , i} и четырехиндексные коэффициенты. По нижним индексам j , k ( j ) проводится суммирование.

Как частный пример задачи (2) рассмотрим антидиагональную систему двух интегральных уравнений Фредгольма с двумя неизвестными функциями u ( x ), v ( x ) :

b u (x) — R 2J K 2( x, s )v (s) ds = f (x), ba                               .     (8)

v ^{( x} ) ^{— R} 2,1 J ^k 2,1 ^{( x} , ^s ) u ^{( s} ) ^ds = ^f > ^{( x} )

a

Решение (8) ищем в виде (9)

u ( x ) = f i ( x ) + £ c fa j ( x ), j = 1

v ⁽ x ) = f 2 ⁽ x ) ⁺ £ ^C j ^j ⁽ x ) j = 1

Невязки системы (8) имеют вид

n

b

<           n

nn

R = £ Cfa ( x ) - Л и J K 1,2 ( x , s ) f 2 ( s ) + E CJ^J (s )

Аналогично, получим, используя систему (12):

' AC1 - 42 BC2 = 42 F2 5                                              , ac 2 - 4 d>c 1 = 4 F1

C² = A ¹ 4 2,1 F ¹ + 4j DC ¹) , AC ¹ - 4 ,₂ BC ² = 4₂ F ² о AC ¹ - 4 1,2 B ( A ¹ 4 2,1 F ¹ + 4д DC ¹ )) = 4 1,2 F ² о C ¹ = ( A - 4 4BA ^{- 1} D )^{- 1} 4 , ₂ F ² + 4₂4д ba ¹ F ¹ ) . (14)

j = 1

n

a

b

V           j = ¹

n

.

R 2 = £ Cfa ( x ) - 41 J K 2,1 ( x , s ) f , ( s ) + £ Cfa ( s )

j = 1

a             V           j = 1

В формулах (13), (14) элементы матриц A, B, D и векторов F1, F2 определяются формулами (11).

Рассмотрим численный пример

Условия ортогональности невязок имеют вид

< R₁, fo _t >= 0, k = 1, n ; < R₂, ^ _k >= 0, k = 1, n . (10)

u ( x ) - J xsv ( s ) ds = x ,

1                                                     , v (x) - J (x + s )u (s) ds = 2 x - 2/3

nb

Запишем 2 n условий формулы (10)

b

n

£ C ¹ J V k ( x > , ( x ) dx - 4 J K 4 x - s fo ( x ) ^f > ( s ) + £ C Jj s ) I dsdx = ⁰

i = 1

n

a

b

a

b

V           J = ¹

/           n

£ C j ¹' . ( x ^fa x ) dx — 4 J ^K 2/ x - sWt ( x ) ^{f (} s ) + £ C fa ^s ) dsdx = ⁰

1 = 1 a

a

V     -

Для упрощения последних формул введем обозначения:

b                       bb ak ,j = J fot (x )faj (x) dx, ft = J j K 2,1 (x, s м (x) f1 (s) dsdx a                       aa bb                              bb bt, j = JJ K 1,2(x, s fa (s 4k ( x ) dsdx, ft = JJ K1,2( x, s fo( x )f2(s )dsdx aa                              aa bb dkJ = J J K’1 (x, s)fa (s)fo (x)dsdx, t, j = 1, n .

aa

4 ,2 = 4 ,1 = 1, K I, 2 ( x , s ) = xs , K ₂ J ( x , s ) = x + s , f 1 ( x ) = x , f , ( x ) = 2 x - 2/3, a = 0, b = 1 .

Пример (15) имеет тот же алгоритм решения, что и задача (8). Вид функций f ( x ) = x , f ₂ ( x ) = 2 x - 2/3 показывает, что линейно-независимые системы состоят из двух функций:

{ ^ ( x ) = 1, fa ( x ) = x } , fo ( x ) = 1, ^ ₂ ( x ) = x } , m = n = 2 .

nn

£ a .  1 - Л* £ b C   4 f t²

j=1

nn

У a„,c 2 - 4 Y d r 1 = 4 f '

t,j j       2,1        t,j   j2,1 j =1

Система двух уравнений (11) допускает матричную запись и ее решение:

' ac ¹ - 4 ,2 bc ² = 4 ,2 f ²

5                                                     .

ac ² - 4 dc ¹ = 4 f ¹

Решая (12), получим такой результат c 1 = a -1 (4 2f 2+4 2bc 2), ac 2 - 4 dc 1 = 4 f 1 о ac 2 - 4 d (a-1 (4 2f 2 + 4 2bc 2 ))=4 F1 о

C ² = ( A - 4 4 ,2 DA ^{- 1} B )^{- 1} (4 , F ¹ + 4 4 ,2 DA ^{- 1} F ² ) . (13)

По формулам (11) находим матричные
элементы для СЛАУ:
1                                                           ______ at , j = J fo t ( x fa j ( x ) dx , k , j = 1,2 , 0
1                                          1 a 1,1 =| ^ i ( x 4 ( x ) dx = J dx = x ^ = 0                         0	1 ,
1                         1           X2 a i 2 = fo l ( xfa ( x ) dx = j xdx = — 0                  0        2		1 2	=	a 2	,1 ,
1                          1           %3 a 2 2 = J fo ( x ) fa ( x ) dx = j x2 dx =— 0                   0         3	1 = 0	1 з ,
11                                                                                          ________ b t,j = J J xs fa{ s fo ( x ) dsdx, t , j = 1,2 0 0	,
11                       11            s2 b 1=| j* xs fa ( s fo ( x ) dsdx =j j xsdsdx = — 11 00                   00          2		1 0	4 2	1 0	£ = 4,
11                      11 b ,2 = J J xs fa ( s ) fo ( x ) dsdx = J J xs 2 dsdx =- 0 0                                0 0		3 3	1 x2 0T		1 1 0 = 6
11                      11 bi, i = JJ xs fa ( s fo ( x ) dsdx = JJ x 2 sdsdx = - 0 0                               0 0		2 2	1 x 0	3 3	1 1 0 =

bi i = j \ xs^i ( s Ж ( x ) dsdx = J J" x² s² dsdx = “ ^,    00                        00               ³

d^ j = j j ( x + s M ( s Ж ( x ) dsdx, k , j = 1,2 , 00

x ³ 3

9,

C 1¹ = о, c 2 = 1, c 1² = 2, c 22 = 1

, подстановкой

^d 1,1

= jj ( x + s ) dsdx =

1                21

s   I  J I x x x s +— I dx = 1 — + —

о V

1        23

^d 1,2

s s   I , I x x x — +— | dx = 1 — + —

I = 1’

^d 2,1

= jj ( x + s ) xdsdx =

o V ²³ J o    V ⁴

1                  21               3

³ J o

12,

убеждаемся, что найденные коэффициенты 2

С 1 = 0, C 1 = 1, C² = j , C 2² = 1       удовлетворяют

СЛАУ (16).

Согласно формуле (3), решение задачи

(15) имеет вид

d 2,2

^f k ¹

^f 1¹

2 xs   I .    ( x x x s +— I dx = 1 — +—

JI о V

1           23

I = ’2’

= jj ( x + s ) sxdsdx = j l x ² — + xs— I dx = I + I b o          o V ²³ J o    V ⁶⁶ J o

11                          11

3,

= j j ( x + s Ж ( x ) f . ( s ) dsdx = j j ( x + s Ж ( x ) sdsdx, k = 1,2 ,

= jj ( x + s ) sdsdx =

f ¹ = jj ( x + s ) xsdsdx = j

1 I s2 s311, I x2   x I1

I x — + —| dx = 1— + -I = — ,

‘    3 Jo     V 4   3 Jo

2, xs31      I x3 x21

x I1 dx = I I1 = o V 2    3 Jo     V 6    6 Jo 3

0 V ²

2 ^s

f k = j j xw_k ( x ) f 2 ( s ) dsdx = jj xs p _k ( x ) ( 2 s — 2 / 3 ) dsdx, k = 1,2 ,

f ² =| [ xs (2 s — 2/3dsdx = | — — —

,    2 x x dx =---

V 6    6

f 2² = jj x ² s ( 2 s — 2/3 dsdx =

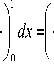
6 ^,

Используя найденные коэффициенты, составим СЛАУ (11):

n

n

I a k,j C j — A ; Z b k , j C 2 = 4 ,2 f k ², k , n = 1,2

j = 1

n

j = 1

n

о

Z a jj — 4 2,1 Z d k /1 = 4 2,1 f k ¹, k , n = 1,2

j = 1

j = 1

a 11 C 11 + a 12 C 1   ^{( ь} _п C 12 + b 12 C 2 ) = ^{f 2}

a ₂₁ C 1¹ + a ₂₂ C 2 — ( b ₂₁ C 1² + b ₂₂ C ₂2 ) = f 22 ' a 11 C 1² + a ₁₂ C 22 — ( d 11 С ¹ + d 12 C 2 ) = f'

„ C ²Г²-^       r¹^ f¹

a₂|C| + a 22 ^ 2 \d 21 C l + d 22 c 2 J— f 2

о

u ( x ) = f ( x ) + C 1 ^ ( x ) + C 1 m ( x ) = x + x = 2 x ,

2  2        ( 17)

V ( x ) = f > ( x ) + C 1 M( x ) + C 2 Ы x ) = 2 x " + j + x = 3 x

Подставляя численно найденные решения (17) в условие примера (15), получим, что

2 x — j xs 3 sds = 2 x — xs

3 x — j ( x + s )2 sds = 3 x-

^; 311 = ^x = ^f 1 ^{( x} )

—

2 2 xs +- s

,   2

= ^{2 x}  _;   ^f 2 ^{( x} )

численное решение (17) является точным в примере (15).

Замечание 1. В некоторых частных случаях, используя дополнительную информацию о правых частях задачи вида (2) или (8), точное решение задачи вида (2) или (8) можно получить с меньшим набором координатных функций. Найдем численное решение примера (18), используя по одной координатной функции (поскольку правые части (18) содержат всего одну координатную функцию степенного вида m ( x ) = x ж ( x ) = x . В этом случае матрицы A, B, D и векторы F¹, F² являются числами.

= x ,

1             ^o

1                                        , v (x) — j xu (s) ds = 2 x o

A ,₂ = 4,i = 1, K 1,2 ( x , s ) = xs, K 2,j ( x , s ) = x , f ( x ) = x , f ₂ ( x ) = 2 x , a = o, b = 1 .

^a 1,1

= j ^ i ( x ) ^ ( x ) dx = j x² dx = — =

C ¹ + 1 C ¹ -1 1 C ² + 1 Cl ¹I = 1

1 2   2 V 4   1 6   2 J 6

¹ C 1 + ¹ C 1 —[ ¹ C 2 + ¹ C ₂ ² 1 = ¹

2   1 3   2 V 6   1 9   2 J 9

о c 2 +1 Cl1 —I C1 + — C1 I = —

1 2   2 V 1    12   ² J 12

¹ C ² + ¹ C ₂² —[ — C 1 + ¹ C 1 1 = ¹

2   1     3   ² V 12    ¹    3    ² J 3

3 ^,

b_v = j j K ,² ( x ’ s M i ( s Ж ( x ) dsdx =

= j xxs • s • xdsdx= — — 33

di, i = j j K ₂ ,i ( x , s M ( s Ж ( x ) dsdx = j j

= 9’

x ³

x • s • xdsdx = —

¹ s ²

6 ^,

bb f2 = П K 1.2 (x ’ s )^‘ (x) f2 (s ) dsdx = aa

1 1

. 3

= j j( xs ) x 2 sdsdx = 2 — — 3„3

0 0

2 ?

bb fl1 =JJ K 2,1 (x - s >1( x ) f.(s ) dsdx = aa

11            10.2 V

С учетом формулы (3) получим невязку для каждой функции решения задачи (2) соответственно в случаях (18) и (19):

N ri(x) = У,(x) exact- У,( x) num = £ J/ x), i = 1 m ,   (20)

J = n + 1

®

r ⁽ x ) = У , ⁽ x ) exact ^- У ^{( x} ) num = £ J ⁽ x )> i = ¹ m •    ⁽²¹⁾

J = n + 1

= j j x • x • sdsdx = П s-x- 2

0 0

f 3         !

dx =| —| =-

1 ⁶ J 0    ⁶

•

Запишем СЛАУ, используя формулу (11), 4 ,2 = 4 = 1 .

1г1-1г2 -2

/11 С ( - b„С 1² = f ²    |з C ¹    9 C ¹ = 9

О С ² - d 11 C 1 = f   | 1 C 2 - 1 C 1 = 1

3    ¹      6    ¹      6

c 1 = 1, c 2 = 1 .

Если системы линейно-независимых функций { ^ ( x ) }Xр{ ^ ( x ) } '₌₁ являются полиномами, то, как показано в работах [1], [2], [3] они выбираются, начиная с самых грубых функций (дающих максимальный вклад погрешности без их использования), например, в виде степенных мономов ( n+1 функция в системе) U ( x ) = К 0 ( x ) = 1, ^ 1 ( x ) = Ы x ) = x ,-,

n ( x ) = К ( x ) = x n } •

Тогда невязки решения в формулах (20), (21) дают одинаковую асимптотику решения:

По формуле (9) получим

^

u ( x ) = f ( x ) + C ^ j ( x ) = x + 1 • x = 2 x , v ( x ) = f ( x ) + C 2 ^ ( x ) = 2 x + 1 • x = 3 x

Сделаем проверку:

1                           3|1

2 x - I xs 3 sds = 2 x - xs   = x = f ( x )

3 x - j x 2 sds = 3 x - ( xs ² ) ₀ = 2 x = f ( x ) 0

В примере (18) найденное численное решение u ( x ) = 2 x , v ( x ) = 3 x является точным. По сравнению с примером (15), в котором вычислено 16 интегральных коэффициентов, в примере (18), мы вычислили всего 5 интегральных коэффициентов, то есть в три раза меньше.

Замечание 2. Предположим, что точное решение задачи (2) имеет разложение по системе координатных функций в виде бесконечного ряда или с конечным числом слагаемых N>n , превышающим число координатных функций { ^ ( x ) } П ₌ р n <  N .

Тогда точное решение имеет вид [1], [2], [3]:

N

У Х x ) exact = ^{f (} x ) ⁺ £ ^C X⁽ x ^ i = ¹ m , j = ^{1 N (18)}

J = 1

или    y ( x ) exact = f, ( x ) + £ Wx ), i = 1, m , J = 1,2,3,- ⁽¹⁹⁾

J = 1

(           )

II r i II = I y exact ^- У num || = ⁰ 1 £ J ⁽ x ) I = ⁰ ( x " J i = ¹ , m •

V J = n + 1          )

Рассмотрим достаточные условия корректности алгоритма (13), (14) численного решения задачи (8).

Теорема 1. Достаточные условия корректности численного решения задачи (8). Пусть матрица A обратима (существуют матрица А ^-1 обратная к А) и выполнено условие 1 4 ,21 | 4 >,1|| рИИ <  q <  1 , тогда алгоритм (13), (14) корректен и верна оценка

I ⁽ A - 4,1 4 ,2 DA-¹ В )^-1| < Ы , q = 4 1,₂| p ₂j р -¹|²| ИИ J ( А - 4,Д ₂ ВА-¹ D )^{- 1}| <  Ы . (23)

Доказательство

Согласно формулам (13), (14) задачи (8)

C ¹ = ( А - 4 ,24,1 ВА -¹ D А ( 4 ,2 F ² + 4 ,24,1 ВА - ¹ F ¹) ,

C2 =(А - 4,14,2 ИА -1 В О F1 + 4,14,2 ИА-1 F2) векторы C1, C2 коэффициентов разложения функций решения u (x), v (x) по системе координатных функций {^,(x)}n=1 существуют тогда и только тогда, если существуют обрат- ные матрицы А 1 и (А - 4,24лВА1 D)1

( А - 4,1 4 ,2 ИА-¹ В )^{- 1} •

,

Матрица А обратима по условию теоремы 1, что обеспечивает существование векторов 4 1,2 F ² + 4 , ₂ Л _2ЛBA-¹ F ¹) , 4 F ¹ + 44 DA ^{- 1} F ² ) в формулах (13), (14) с конечной нормой 1 4 ,2 F ² + 4 ,₂ 4 BAF Ч < » ,| ^ 2,1 F ¹ + 4,1 4 ,2 DA ^' F ²| < ».

Отметим,        что        условие

| Ад 4 IIA   IbIIIIDI - q <1 является общим для матриц (A - 44BA-1D)-1 , (A - 44 2DA ' B)-' , поэтому достаточно доказать обратимость одной из матриц.

Так как матрица Z представима в виде произведения двух матриц

Z = A - 44 BA ¹ D = A ( I - 44 A ^{- 1} BA ^{- 1} D ) , то если матрица Z обратима, получим Z ^- = ( l - 4,2-4, i A ' BA ^- D ) 1 A ^- . Здесь I — единичная квадратная матрица размерности ( n х n ). По условию Теоремы 1 выполнено условие 1 4 ,21 4 2,111 A     |b |II| d |I - q <  1 , следовательно,

( I - 4 1,24д A-¹ BA -¹ D )^{- 1} = £ ( 4 ,2 Л 2Д ) k ( A -' BA ^{- 1} D ) k k = 0

^

Z ^{- 1} = I £ 4 1,24,1 ) k ( A ^{- 1} BA ^{- 1} D У I A ^{- 1} . k k = 0                           J

С учетом последней формулы и условия 14,2 4 |||A   |b||||d|| - q < 1 оценим по норме матрицу Z 1

^

||^Z -^{1 -}| £ 4 ,241Z⁽ A" ^{BA -1 D} ) k ||| A -*||^-k k =0                            J

4Я д у 44 1 A -fi b m 1 ' ) a 11k k = 0                              J J

“

-Is qk III A-'ll = k k=0 J

I A 11

' - q '

Теорема 1 доказана.

Сравним условия корректности в диагональной задаче (24) из системы уравнений Фредгольма второго рода с условиями корректности численного алгоритма для одного интегрального уравнения (частный случай системы уравнений (24) при i=m =1): b

У, ( x ) - 4 J K iii ( x , s ) y j ( s ) ds = f, ( x ), i = ', m •     (24)

a

Система (24) имеет решение и невязку:

n

У , ⁽ x ) = ^{f ( x} ) ⁺ £ C ^{4 ( x} ) ⁱ = ', ^m , J = ', ⁿ , j = '

Требуем ортогональности невязок всем n линейно-независимым функциям второй системы    4 ( x ) }4   <  R 4 >= 0, i = 1, m , l = 1, n

.)                      bb                I                    1

£ C J 4 (x4 (x)dx - 4 J JK,,- (x, s41 (x)| f (s) + £ C4 (s) |dsdx = 0, j ='    a                           aa ’               k          j='           J i = 1, m, j, l = 1, n n     b                         n     bb

£ Ci J 4 (x'4l (x)dx - 4., £ C'j J J Ki (x, s4 (x4 (s)dsdx = j='     a                                j='     a a bb

= 4.i J J Ki,i (x, s41 (x)fi (s)dsdx, i = 1, m, j = 1, n (25) aa b                     bb al.j = J 4(x4 (x)dx - 4 J J Ki,i(x,s4 (x4 (s)dsdx a                     aa i = 1, m; I, j = 1, n bb fi = 4.i J J Ki,i (x, s)4l (x)f (s)dsdx, i = 1, m, I = 1, n .

aa

Тогда формула (25) примет простой вид:

АС = F4 C = (A ) ^- ' F' , i = ', m .       (26)

В формуле (26) A¹ ( n х n ), i = 1, m матрица коэффициентов с номером i, C‘ ( n х 1), i = 1, m -вектор-столбец размерности n с номером i . F ' , i = ', m - вектор-столбец правой части в i -й строке системы интегральных уравнений (высоты n) . Все указанные коэффициенты определяются формулой (25). Как показано в работах [1], [2], [3], для одного интегрального уравнения Фредгольма в системе уравнений (26), решение существует и единственно тогда и только тогда, если det ( A ) * 0 , соответственно в (26) det( a' 4 0, i = 1, m , что дополнительно накладывает ограничения. Ограничения на элементы матриц A , i = 1, m , в том числе на величину параметров 4 , и норму интегральных ядер || K , ₍ .||, i = ', m .

Разобьем матрицу A ( n х n ), i = 1, m на разность двух матриц и введем обозначения:

b

bb

bij = J4(x4(x)dx = bд dij = JJK Xx,s4(x4(s)dsdx, a                            aa a‘ = b ,-44 ^ A = B-4,D,,i = 14m .   (27)

. j                   , j                   ,           . j                                                               , i

Докажем Теорему 2.

Теорема 2 (достаточные условия корректности алгоритма (25),  (26)). Пусть матрица B в (27) обратима и выполнены условия   |4, IBB 41 | D || - qi < 1, i = 1, m, max qi = q < 1 , тогда алгоритм (26) вычисления коэффициентов C, i = 1, m корректен.

Верны оценки:

I ( ^ fl <  t J, i = 1, m .         (28)

Доказательство

По условию Теоремы 2 матрица B обратима, тогда a = в - 4.d = в (i - \ вd ) i = 1,m.

Тогда формула (26) C‘ = ( A ) ' F‘ , i = 1, m корректна, если и только если обратимы матрицы

A = В ( I - A i, i B D_t} i = Г т ,

A ^ z i = в ( I - a , i B 1 D i ) z i ' = ( I - a , i B 1 D i )^{- 1} В 1 .

По условию Теоремы 2 A|||в ¹ |А 1|< qi <  1, имеем:

Z,  = ( I - A в D_t ) ^{- 1} В = I £ (а г В ' D_t У I В , i = r m .

i              i ’ i        i'            I k-A ‘i' J

Последнюю матрицу Z_t ^-1 оценим по норме

-»

М<Ш A , B -Hl в -Wz q j в - <

• < k=0                  J        V k=0

( -    \     „   ||в “Ml ____

• <| z q ^k I в-¹ = P , i = 1, m .

I k~0   J   11

Теорема 2 доказана.

По сравнению с одним интегральным уравнением Фредгольма второго рода в диагональной задаче с системой интегральных урав-нений(24) (Теорема 2) требуется не только обратимость матрицы B с одним условием |A||в'|||D || <  q <  1 , но и m неравенств (условий-ограничений | A ||В ¹1| Ц а 11 <  q_i , i = 1, m, max q_i = q <  1 ).

В работе получены основные результаты:

• 1)    Поставлена задача для системы интегральных уравнений Фредгольма второго рода с непрерывными ядрами на квадрате K i , j ( x , s ) e C ( [ a , b ] x [ a , b ] ), i , j = 1, m . Введено определение диагональной задачи и ан-тидиагональной задачи.

• 2)    Впервые для задачи общего вида (2) предложен алгоритм ее численного решения обобщенным проекционным методом Петрова–Галеркина (3)–(7). Идея состоит в требовании ортогональности m

невязок интегральных уравнений системы к n функциям второй линейнонезависимой системы { ^ ( x ) } ’₌₁ . Предложен алгоритм решения антидиагональной системы двух уравнений Фредгольма второго рода (8)–(14). Формулы (13), (14) матричного вида для коэффициентов разложения C 1 , C ² e R n решения u ( x ), v ( x ) по первой системе {^ ( x ) } А функций. Указана формула для невязки неизвестных функций между точным и численным решением.

• 3)    Используя алгоритм (8)–(14) численно решены два примера (15) и (17), в которых численные решения примеров совпали с точными решениями.

• 4)    Доказаны Теоремы 1, 2 (достаточные

условия корректности численных алгоритмов (13), (14) для антидиагональной задачи с двумя уравнениями Фредгольма и (25), (26) для диагональной задачи (24) общего вида).

Отметим также, что решение краевых задач в частных производных иногда сводится к решению интегральных уравнений [5], [6], [9]. Последние 10 лет активно изучаются уравнения с производными дробного порядка, сводимые к интегральным уравнениям [10].