Обобщение модели двойного сдвига для учета эффекта вязкости при плоско-деформированном состоянии

Модель двойного сдвига была предложена для описания движения гранулированных материалов [1] (также см. обзор [2]) и учитывает зависимость условия текучести от среднего напряжения и пластическую несжимаемость, характерные для этих сред (в дальнейшем эту модель будем называть оригинальной ) . Однако подобные свойства присущи и некоторым металлическим сплавам, хотя угол внутреннего трения (в терминологии механики гранулированных материалов) в этом случае достаточно мал [3–6]). Для авторов работы [4] это послужило основанием для применения модели двойного сдвига к описанию пластического течения металлических материалов. В публикуемой работе обобщенная модель двойного сдвига также распространяется на традиционные металлические материалы.

Оригинальная модель двойного сдвига может рассматриваться как обобщение классической теории идеально-жесткопластического материала, изложенной, например, в [7]. В частности, уравнения модели двойного сдвига при нулевом угле внутреннего трения сводятся к уравнениям теории идеально-жесткопластического материала. Свойством переходить в модель идеально-жесткопластического материала при обнулении некоторых параметров обладают и многие другие модели, предложенные для гранулированных материалов [2]. Оказалось, однако, что характер поведения решений, полученных по разным моделям, качественно различен и может не совпадать с соответствующим характером поведения идеально-жесткопластических решений [8–11]. При этом угол внутреннего трения может быть как угодно мал. Основным источником этого различия являются условия на поверхности максимального трения. В частности, при проскальзывании поле скорости в окрестности таких поверхностей, вычисленное в рамках модели идеально-жесткопластического материала [12], является сингулярным (эквивалентная скорость деформации стремится к бесконечности, то есть некоторые пространственные производные от компонент вектора скорости перемещения не существует). В приложениях невозможно указать точную границу, разделяющую области применения той или иной модели. Поэтому при обобщениях модели идеальножесткопластического материала с целью учета тех или иных особенностей сопротивления материала пластическому деформированию, желательно, чтобы качественное поведение решений не изменялось по сравнению с исходной моделью. Решения конкретных краевых задач [8, 10, 11, 13–16], а также общий анализ системы уравнений [17, 18] показывают, что поле скорости в решениях по модели двойного сдвига в окрестности поверхностей максимального трения является сингулярным при проскальзывании и его асимптотическое представление совпадает с полем скорости в решениях по модели идеально-жесткопластического материала. В связи с этим из всех других моделей, учитывающих зависимость условия текучести от среднего напряжения и влияние вязкости на сопротивление материала пластическому деформированию, в публикуемой работе за основу взята модель двойного сдвига. Определен класс вязкопластических моделей с условием текучести, зависящим от среднего напряжения, приводящих к решениям, качественное поведение которых вблизи поверхностей максимального трения совпадает с поведением решений для других моделей материалов [12, 17, 18].

Рассматривается задача плоско-деформированного состояния материала.

Уравнения модели двойного сдвига при квазистатическом плоском течении в декартовой системе координат приведены в [1]. В произвольной ортогональной системе координат ( O, а, в ) (см. рисунок) эти уравнения имеют вид:

д(HР°™ ) д(Hа^р )    5H 5H а              р да          др       ар др     вв да

д(HаО„ ) + д(Hв”а, ) + дH, _ дHа _ др         да      ав да    аа др

₂           12

( ° аа ^_ ^р ) ^{+ 4} ° ар    ⁺( ° аа ⁺ ^ рр ) sin Ф ^{_ 2 k} cos Ф ;

^ аа + ^З р _ 0 ;

2^ ар cOS 2у ^_ ( ^ аа ^_ ^ рр ) ^{sin 2}Ф + ^2sin ф ( ® ар ^{+ d} ф/ ^dt ) ^{_ 0} •

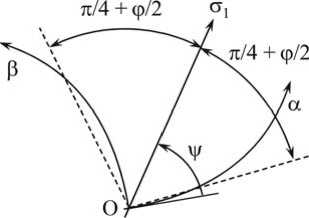
Произвольная ортогональная система координат ( O, а, в )

Здесь выражения (1) — уравнения равновесия, (2) — условие текучести Кулона-Мора, (3) — уравнение несжимаемости, (4) — уравнение связи напряженного и деформированного состояний, полученное из предположения, что деформация происходит за счет сдвига вдоль характеристических направлений уравнений (1) и (2) (эти направления показаны на рисунке пунктирными линиями). Кроме того, H _α и H _β — коэффициенты Ламе; σ _αα , σ _ββ и σ _αβ — компоненты тензора напряжения; ξ _αα , ξ _ββ и ξ _αβ — компоненты тензора скорости деформации; ω _αβ — компонента тензора вращения; ψ — угол между касательной к α -линии и направлением максимального главного напряжения σ ₁ , отсчитываемый от касательной против часовой стрелки (см. рисунок); d ] dt — полная производная по времени; ф — угол внутреннего трения; k — коэффициент сцепления (в терминологии механики сыпучих сред).

Зависимость компонент тензоров скорости деформации и вращения от компонент скорости u _α и u _β имеет вид [1]:

^{1 5} u а + u в   д Н а       ? = ^{1 5} u в +   u «   ^{5 Н} в

Н _а 5 а   Н _а Н _в 5 в , ^вв   Н _в 5 в   Н _в Н _а 5 а ,

25   = ^{1 5} u в + ^{1 5} u а - u а   ^{5 Н} а - u в   ^{5 Н} в

^4ав Н _а 5 а Н _в 5 в Н _а Н _в 5 в Н _а Н _в 5 а ,

2_Ю   = 1 5 и а __ 1_ ⁵ u в + и а   5Н а - u в   ^{5 Н} в

^Юав   Н _в 5 в   Н _а 5 а   Н _в Н _а 5 в   Н _в Н _а 5 а ^.

Отметим, что характеристики для уравнений (1), (2) совпадают с характеристиками для уравнений (3), (4), в которых компоненты тензоров скорости деформации и вращения должны быть исключены с помощью соотношений (5) [1, 13].

В модели двойного сдвига, предложенной для гранулированных материалов, ф и к — постоянные величины. При ф = 0 система уравнений (1)-(4) сводится к системе уравнений плоско-деформированного состояния идеального жесткопластического тела. При этом необходимо учитывать, что k — предел текучести при чистом сдвиге. Общепринятое обобщение идеально-жесткопластической модели, позволяющее включить в рассмотрение эффект вязкости, состоит в предположении, что предел текучести зависит от эквивалентной скорости деформации [19], которая при плоском течении определяется соотношением:

5 eq = 723 ( ^ 2а + ^ 5, + 2 . . )” = 2^3 ( ^а + 5 . j’’ = 2/73 ( . + ^ Г ' (6)

Последние два равенства являются следствием уравнения несжимаемости (3).

Для металлических сплавов угол ф мал, поэтому обобщение модели двойного сдвига, учитывающее эффект вязкости, заключается в предположении, что ф — постоянная величина, и k в уравнении (2) зависит от ξeq . Условию текучести (2) можно удовлетворить подстановкой соотношений oaa = ° (1 - sin Ф cos 2ф) + k cos Ф cos 2ф, opp = ° (1 + sin Ф cos 2ф) - k cos Ф cos 2ф, °ав = k cos ф sin 2ф -с sin ф sin 2ф,

из которых следует, что с = ( с_аа + с_рр ) /2.

Рассмотрим возможность возникновения поля скорости, приводящего к условию ^ eq >да вблизи определенных поверхностей. Только при его выполнении качественное поведение решений по новой модели может совпадать с качественным поведением идеально-жесткопластических решений. Очевидно, что сформулированное условие зависит от вида функции k ( £ _eq ) . В частности, если k ( £ _eq ) ^от при ^ _eq >да, то, как показано в [20, 21], для вязкопластических моделей с условием текучести, не зависящим от среднего напряжения, на поверхностях максимального трения, около которых в идеально-жесткопластических решениях обычно возникают сингулярные поля скорости, имеет место условие прилипания и поле скорости не является сингулярным. С другой стороны, для таких же вязкопластических моделей показано [22, 23], что сингулярные поля скорости возможны, если k ( £ _eq ) ^ k s = const при £ _eq >да. Кроме того, в [22] отмечается, что любые экспериментальные данные могут быть аппроксимированы с одинаковой точностью как зависимостью вида k ( ^ _eq ) ^ k s = const при £ _eq >да, так и зависимостью k ( £ _eq ) ^да при £ _eq >да. Поэтому здесь предположим, что k ( ^ _eq ) ^ k s = const при £ _eq ^ да , где k s — предел текучести материала при стремлении эквивалентной скорости деформации к бесконечности или напряжение насыщения. Такие зависимости сопротивления материала от эквивалентной скорости деформации имеют место при определенных условиях [24].

Подставляя (5) в (3) и (4), получим

1 5 u    1 5 u„   u„ d ln H   u 5 ln H

--°- +--^+—^--° + _i--H = 0 H _a da   H _e dp   H _e дв    H _a da

( cos 2ф - sin ф ) d u _p   ( cos 2ф + sin ф ) d u _a sin 2ф d u _a sin 2ф d u _p

H O             H p     ^F   HC     H _p "dp

u	f     d ln H	-- cos2ф ^a	. •    d H	, „ .    dф
	sin 2ψ		+ sin ф---—	+ 2sin ф—
H α	d a V	H p d P	H p d p	d a
u β	f      d H p cos 2ψ	. d In H + sln2 ф------	.    d H p + sin ф---—	э •    dф - 2sin ф—
H в	V       H a d a	d p	H a d a	d p

-

+ 2sin ф — = 0. d t

Рассмотрим краевую задачу, включающую закон максимального трения в качестве одного из краевых условий. Систему координат выберем так, чтобы эта поверхность трения совпадала с одной из координатных линий: либо a = 0, либо p = 0. В дальнейшем, в рамках одной и той же краевой задачи будем рассматривать одновременно оба эти случая (различия заключаются только в выборе системы координат). Предположим, что пластический материал в окрестности поверхности трения занимает область а > 0 (или в > 0 )• Сингулярные поля скорости, аналогичные случаю идеально жесткопластического материала, могут возникать, только если сдвиговая скорость деформации стремится к бесконечности при приближении к поверхности трения. Положим сначала, что поверхность трения совпадает с координатной линией а = 0. В этом случае компоненты вектора скорости и их производные по β ограничены на поверхности трения. Тогда из (5) следует, что условие | ^ар | ^” при а ^ 0 выполняется, если только |дир/да| ^да при а ^ 0. Далее, рассмотрим случай, когда поверхность трения совпадает с координатной линией в = 0. Теперь на поверхности трения ограничены компоненты вектора скорости и их производные по а, и из (5) следует, что условие |^а₽| ^ да при в ^ 0 выполняется, если только |диа/дв| ^ да при в ^ 0. Если условие |^ар| ^ да выполняется при приближении к поверхности трения, то такую поверхность будем называть поверхностью максимального трения. Так как на поверхности максимального трения выполняется условие | ди а /др| >да (или |д и в /5а| >да ), то коэффициент при соответствующей производной в уравнении (9) должен обращаться в нуль (иначе это уравнение не может иметь решения), а на поверхности максимального трения выполняется равенство:

cos 2* - sin Ф = 0         (а = 0)                                                  (10)

или cos 2* + sin ф = 0        (в = 0).                                                    (11)

Уравнения (10) и (11) выражают закон максимального трения для рассматриваемой модели материала. В таком же виде этот закон используется в модели двойного сдвига и может быть сформулирован для идеально жесткопластических материалов, хотя в последнем случае общепринятая формулировка имеет вид: т f = к , где т f — удельные силы трения при проскальзывании. Как следует из уравнений (10), (11) и рисунка, касательная к поверхности максимального трения совпадает с характеристическим направлением системы уравнений (1)–(4), а поля скорости получаются сингулярными, если поверхность максимального трения есть огибающая семейства характеристик. Отсюда следует математический смысл закона максимального трения: решение не может быть продолжено за поверхность максимального трения.

Для общего анализа свойств уравнений нет необходимости рассматривать оба условия (10) и (11), поскольку всегда можно выбрать систему координат так, чтобы выполнялось любое из них. Однако при решении конкретных задач более удобным может оказаться либо то, либо другое условие. Различие в формулировках (10) и (11) связано с тем, что угол ψ отсчитывается от α -линии. В дальнейшем, для определенности, будем считать, что поверхность максимального трения совпадает с линией в = 0, на ней выполняется условие (11). Таким образом, в случае проскальзывания имеем п ф

* = *„ = -+-.

Кроме того, в некоторой окрестности линии в = 0 систему координат всегда можно выбрать так, что линии в будут прямыми и H _р = 1 .

Воспользуемся символами порядка о и O [25], где o(av) — малые более высокого порядка, чем av, а O (av) — малые порядка sv. Асимптотическое поведение поля скорости, определяемое из решений системы уравнений (8), (9), будет совпадать с соответствующим поведением идеально жесткопластических решений [12], если и а = U0 + 2U1в12 + о (в12), в ^ 0,

где U ₀ и U 1 — некоторые функции, зависящие от а . Раскладывая сумму ( cos2y + sin ф ) в ряд в окрестности точки у = у w , получим:

cos2у + sin ф = - 2cos ф ( у - у _w ) + о ( у - у _w ) , у ^ у _w .

Без ограничения общности можно считать, что поверхность трения неподвижна и, таким образом, перемещение и в = 0 при в = 0. Все члены уравнения (9), за исключением второго, ограничены (это следует из ранее сделанного предположения об ограниченности компонент вектора скорости и их производных по α на поверхности трения). Значит, второй член тоже должен быть ограничен. Это возможно (см. (13), (14)), если у = У. + -nH— в1'2 + о (в12), U1 cosф        х 7

в ^ 0.

Асимптотическое представление компоненты скорости uβ вблизи поверхности максимального трения получается из (8) и (13) и имеет вид:

и в = V i в + V 2 в ³² + о ( в ³ 2 ) ,    в ^ 0 ,

где V ₁ , V ₂ — некоторые функции, зависящие от α . Положим, что зависимость k от ξ _eq при неограниченном возрастании эквивалентной скорости деформации принимает форму:

k = k s ^Ф( 5 eq ^ 0 ) = ^ks ^Ф ( n ) = k s [ 1 ^-ф » n - ^{Y + 0} ( П -^ ) ] ,    П >» .                  (17)

Напомним, что k ( ^ _eq ) ^ k s = const . Кроме того, здесь 4 0 — некоторая характерная скорость деформации, являющаяся параметром модели материала, ф » — безразмерный коэффициент, величина которого не оказывает влияния на качественное поведение решения, п — безразмерная скорость деформации, у > 0 и 5 >  0 — постоянные.

Убедимся, что разложение (15) и зависимость (17) совместимы с уравнениями равновесия (1). Подставляя (7) в (1) при H в = 1 , имеем:

+ H a

H α

sin ф cos 2 и ) + k cos ф cos 2 ф J

da d (k cos ф sin 2ф -a sin ф sin 2 и)

d e

. _ x d H.    _

+ 2 ( k cos ф sin2y - о sin ф sin2^ ) ^ p^- = 0,

2ф ) - k cos ф cos2y )

"dp                +

+ 2 ( о sin ф cos 2ф - k cos ф cos 2ф )

dH   d ( k cos ф sin2y - о sin ф sin2y )

—- +— ------------------ = 0.

d p

d a

Нормальные скорости деформации ограничены при приближении к поверхности максимального трения. Поэтому из (5) и (6) при p ^ 0 следует:

eq

∼

73~ *1

∼

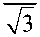
^d u a d p

Подставляя (13) в (19), найдем n=—=₽-1'2+o(в4,2), ₽>o.(20)

ξ0

Используя (17) и (20), получим

Ik = dk ^ = о (в”2), в > 0.(21)

da dn da

Таким образом, в уравнениях (18) все слагаемые ограничены, за исключением тех, которые содержат производные по p . Следовательно, последние также должны быть ограничены, то есть

d ( k cos ф sin 2 ф -a sin ф sin 2 ^ )

dp

= O ( 1 ) , p >  0;

d [a ( 1 + sin ф cos 2 ф ) - k cos ф cos 2 ф]

dp

= O ( 1 ) , p >  0.

Рассмотрим производную d k /dp . Выражение для нее получается из (17) и (20):

д k _ dk dp dp = d n dp

= о ( p - ^{1 +Y/ 2} ) , p> 0.

Подставляя (23) в (22), можно убедиться, что равенство (22) выполняется, если у >  2 . Из ограничения на величину у непосредственно видно, что предположение о том, что зависимость k ( n ) при n >^ представляется степенной функцией (уравнение (17)), не существенно, и более общая зависимость, при которой соотношения (22) выполняются, имеет вид:

— = A П - 2 + o ( п - 2 ) , П^” ,

где A — коэффициент, определяемый моделью материала, и возможно выполнение условия A = 0 .

Таким образом, асимптотическое поведение поля скорости вблизи поверхности максимального трения для новой модели качественно совпадает с соответствующим поведением для оригинальной модели двойного сдвига и, следовательно, для классической теории пластичности идеально жесткопластических материалов, если зависимость коэффициента сцепления от эквивалентной скорости деформации имеет вид (24). Форма этой зависимости при п < ” не играет роли, за исключением случая d—d п >  0. Поскольку из-за бесконечных значений эквивалентной скорости деформации, входящей в это соотношение, экспериментальное определение зависимости (24) не представляется возможным, то приведенный теоретический аргумент о совпадении асимптотического поведения решений с известными моделями выглядит обоснованным и его желательно учитывать при выборе той или иной зависимости — ( п ) . Отметим, что этот выбор никак не ограничивает поведение функции — ( п ) на любом заданном интервале изменения п , на котором могут быть получены экспериментальные данные. Однако использование зависимости (24) требует специальных численных алгоритмов, учитывающих сингулярный характер решений в окрестности поверхностей максимального трения.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-01-92011 ННС_а), Совета по грантам Президента РФ для ведущих научных школ (грант НШ-134.2008.1) и молодых российских ученых (грант МК-5157.2008.1).