Обобщение открытой космологической модели с излучением

В [1] для модели открытой Вселенной записаны отдельно решения для некогерентной пыли и равновесного излучения в синхронной системе отсчета в параметрическом виде, что несколько затрудняет исследование. Кроме того, каждое из упомянутых космологических решений уравнений тяготения справедливо для определенной области изменения временного параметра и не переходит одно в другое. При этом эти решения отвечают разным уравнениям состояния, то есть каждое из них описывает конкретную материальную среду. Поэтому вполне естественно стремиться получить космологическое решение для открытой Вселенной, которое было бы свободно от этих недостатков.

Найденные в работах ( [2]- [3]) точные космологические решения, могут служить такими примерами. Эти решения описывают для больших времен асимптотическое поведение пылевой материи (с давлением пыли pdust = 0) и равновесного излучения с уравнения состояния p _r&d = £rad/3 ( p rad —давление ii frad — 'Энергетическая плотность равновесного излучения).

Подход, использованный в ( [2]- [3]) связан, в частности, с [4], где метрика, конформная метрике Минковского (конформно-галилеева метрика), используется для описания открытой космологической модели Фридмана (с отрицательной скалярной кривизной)

ds2 = ехр(2о)8н" dx*dx",                                    (0.1)

г je а = o(S); S² = Bpv x^M x^v = t² - r²; Bpv = diag(1 ； —1; —1; —1); 〃， v = 0,1, 2, 3 ： скорость света 口 гравитационная постоянная Ньютона равны единице.

Система уравнений Эйнштейна

Gpv = Rpv - 2 gpv R = ^{— K}Tpv                             (、°- 2)

с тензором энергии-импульса идеальной жидкости (ТЭИ)

T^v = fuHuv + pbpv ,                                   (。- 3)

rje f — плотность эіі ( ?ргіш ： p — давление ： к — < ) пііштепповская гра.вігтатіііоішая постоянная, равная здесь 8п u_M = exp(b)bp, — 4-скоросіъ c u^U = 1; b^ = S,/ b^,” = u_MUv — gpv — 3-проектор на 3-простраііство. a bp”u* = 0, может быть сведена к системе 口 з двух уравнетшіі путем проектирования на временноподобную мировую линию и пространственноподобную поверхность, ортогональную временноподобному направлению:

³(² ! + ⑺ 2)

Kf • exp(2a);

- 2 (。〃 + 芳 +

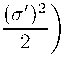
кр • exp(2a) 三 4h(S),

(0.4)

(0.5)

где штрих обозначает производную по переменной S, a h(S) является некоторой функцией, связанной с давлением.

В дальнейшем уравнение (0.4) будет служить определением плотности энергии. Уравнение (0.5) заменой а = 2 • ln(y) преобразуется в ура.віі ( ?іш ( ? типа Штурма-Лиувилля.

у" + 2 y' + h(S)y = 0,                                    (0-G)

S где у = y(S).

Проведение аналогии с движением частицы единичной массы для новой переменной x = 1/S в силовом поле [6],

F = -~тU = h(x)y 三 B2y, dy c B = const, по：зво,「яет переписать уравнение (0.6) в 巾0PMe уравнения для осциллятора у'' + B2 у = 0,(0-8)

где в дальнейшем штрих будет обозначать производную по переменной х.

Решение этого уравнения [2] может быть представлено в виде

у(х) = exp(a/2) = (l/cosao) • cos(Bx + a°) =，1 + (A/B)2 • cos(Bx + a°), rje tgao = A/B; A ii B - парам(?тры. свя：заішы(?. cootb(?tctb(?iiiio. с наблтодаемой плотиостьто веше-ства и равновесным излучением. Конформный множитель из (0.1) отвечает открытой Вселенной, заполненной веществом и равновесным излучением и связан с функцией у(х) как у4 = exp(2a) ([2]- [3]). При этом постоянная A входит в решение Фридмана для открытой модели Вселенной (см., [4]), которое может быть получено из (0.9) при B т 0, exp(2a) т ехр(2ағ)

(1-"

(0.10)

Уместно подчеркнуть, что метрика (0.1) в форме Фока может быть сведена к записи метрики в синхронной системе отсчета из [1], ds2 = dt2 — a(t)2(dx2 + shx2(d。2 + sinӨ2d^2)),

(0.11)

путем перехода в кинеметрическую систему отсчета [5]. Здесь t — временная переменная; а, х, Ө, ^ суть четырехмерные сферические координаты, где a(t) есть радиус кривизны Вселенной.

Кроме того, решение [2] в записи (0.9) можно связать с функцией Бесселя полуцелого порядка.

Такое обобщение проведено в работе [3].

1. Метод Дар бу

Воспользуемся методом Дарбу ( [7]; [8], с.176), чтобы получить обобщение решения [2]. Суть этого метода для уравнений типа уравнения Штурма-Лиувилля в применении к данной задаче состоит в следующем.

Без ограничения общности перепишем общее решение (0.9) уравнения (0.8) в виде

Ytotal(x)三 Y = Yo • Sin(Bx + 夕0), rj,e 夕o - новый сдвиг(})а：зы.

Возьмем одно из частных решений уравнения (0.8)

Ypartial (х)三 Y(x)= COS(B£X), rje £ — некоторая положительная постоянная.

Тогда уравнение

% + Q2(x) Y 三 ％ + [B2 + W(x)] Y = 0,(1-3)

обобщающее уравнение (0.8), имеет следующее общее решение:

Ytotal(x) = YX — Y • (ln Y)Xx, при этом функция W(x) обязана быть равной

W(x) = 2 • (ln Y) 厶 =-2B2e² sec²(Bgx)

(1.5)

2. Новое космологическое решение для открытой Вселенной

Применим описанный здесь метод Дарбу к решению [2]. В исходных обозначениях обобщение открытой Вселенной Фридмана на случай присутствия излучения представляет собой решение,

y(x) = УоВ (cos(Bx + go) + g sin(Bx + 屮。 )tg(gBx)),

(2.1)

уравнения

y 〃 + В²(1 - 2 g² sec²(gBx)) y = 0,

(2.2)

которое при g = 0 переходит в (0.8). цде уо — некоторая постоянная.

Естественное требование, накладываемое на полученное решение, - это асимптотическое прохождение данного решения через фридмаиовское (0.10) (S т х и ли x т 0). Это требование приводит к системе алгебраических уравнений на параметры решения:

УоВ cos(go) = 1;

(1 — g2) • УоВ sin(go) = A.

(2.3)

Отсюда получаем соотношение

tg ao tg(go) = 1 - g2， связывающее начальную фазу нового решения с начальной фазой решения [2].

С учетом (2.3) выражение (2.1) переписывается в виде, аналогичном записи (0.9),

(2.4)

y(x) = (1/cos go) • (cos(Bx + go) + g sin(Bx + go) tg(gBx)),

(2-5)

Ясно, что для найденного решения можно записать и новые результирующие распределения плотности энергии и давления вещества и излучения.

Перепишем гравитационные уравнения для плотности энергии и давления (0.4) и (0.5) через новые переменные y(x) и x :

KE (x)

^12Bx3 g^(x,g) y(x)^{4 f (x}, ^g)

5 — О；

(2-6)

4B2x2 ,

^Kp(x)= 而 ° - ^{2gsec (B} ⑵) '

(2-7)

где

g(x, g) = (g2 — 1) tg(Bx + go) + g tg(gBx) • f (x, g);

(2-8)

f(x,g) = 1 + gtg(Bx + go) • tg(gBx).                              (2-9)

Выражение для плотности энергии (2.6) при g = 0 совпадает с плотностью энергии в [2]:

KEBS (x)

12Bx³ …              …      、

—  4 tg(Bx + ao)(1 + Bx • tg(Bx + ao)

y(x)

(2.10)

и асимптотически (S т х и ли x т 0) превращается в сумму плотностей энергии вещества и излучения kebs (x) = KEdust + KE” = 12Ax3(1 + Ax) + B2x4 = 12A(1/S)3(1 + A/S) + B2(1/S)4.   (2.11)

Найденное давление (2.7) для асимптотики принимает вид кр(х) = 4B2(1 - e2)x4 = 4B2(1 - e2)(1/S)4                       (2.12)

ii при £ = 0 переходит в асимптотическое выражение для давления равновесного излучения prad в работе [2].

Введем функцию состояния, то есть функцию, которая в каждый момент времени представляет собой уравнение состояния, p — 1 Bx • (1 - £2sec2(B£x)) • f2(x, £) _=--:...-..:------:...------...-~

⑵ 13)

е 3 g(x,£) • (Bx • g(x, £) -f(x,£))

Функция в(х,£) 口 пределе £ т 0 переходит в 小 ункишо состояния для случая [2].

〜 八          、    1 Bx ctg(Bx + an)                           .    .

^{в( ， £)    eB}S( )   3(1 + Bxtg(Bx + a 。 ) ) '

которая, в свою очередь, при A = 0, то есть tga 。 = 0, (вещество отсутствует) асимптотически равна

B bS ^{(x) т} 3.

(2.15)

• 3.    Заключение

С помощью метода Дарбу ( [7]- [8]) получено новое космологическое решение для открытой модели Вселенной. Это решение является обобщением космологического решения, найденного ранее и описывающего открытую Вселенную с веществом и излучением (см. [2]), переходя в него для предельных значений параметров, входящих в полученное новое решение.