Задачи о расчете установившихся откликов линейных систем на периодические внешние воздействия традиционно занимают важное место в теоретической физике. В частном случае простейшего воздействия в виде гармонической функции откликом будет частотная характеристика системы, знание которой позволяет в рамках спектрального метода найти реакцию системы на воздействие произвольного вида. В случае систем, состояние которых описывается дифференциальными уравнениями в частных производных, периодические режимы будут порождать распространяющиеся в материальной среде волны той или иной природы.

Если иметь в виду потребности практики, то большое значение для проведения оценочных расчетов имеет теоретическое рассмотрение указанных волновых задач для областей с простой геометрией, а именно – для областей в виде шара, цилиндра, пластины и полупространства. В теории электромагнетизма здесь можно указать на задачу о расчете коэффициентов отражения и пропускания при падении плоской гармонической электромагнитной волны на однородную пластину [1, с. 581–585], на задачу о выводе формул для коэффициентов отражения и проникновения (формул Френеля) при падении такой же волны на

однородное полупространство [2, с. 162–172], а также на задачу для телеграфного уравнения при исследовании волн в конечных и полубесконечных линиях передачи [3, с. 557–568]; в теории тепломас-сопереноса – на статьи [4–6], где рассматривается сушка влажной пластины электромагнитными волнами при периодическом изменении интенсивности излучения; в теории теплопроводности – на классическое руководство по теоретической физике [7, с. 542–549], в котором исследуется прохождение тепловых волн сквозь пластину при гармонических граничных условиях 1-го и 3-го рода, и на монографию [8, с. 298–313], где при той же постановке проблемы исследуется еще и задача для полупространства, а также на известную в науке задачу Фурье о колебаниях температуры в поверхностном слое земной коры, вызванных сезонными изменениями температуры воздуха [9, с. 238–247]. Решения всех перечисленных выше задач находят важные применения на практике; в частности, решение задачи Фурье, которая ставится как задача для полупространства, принадлежит к числу основополагающих теоретических фактов в мерзлотоведении ( геокриологии ) и представляет собой важный инструмент при решении проблем метеорологии, климатологии и охраны окружающей среды, а также при строительстве зданий и развитии сельского хозяйства в области распространения мерзлых пород [10; 11]. Существенным

LM^^e © Афанасьев А.М., Бахрачева Ю.С., 2021

Воздушный поток с переменной во времени температурой

Влажный материал

7в(т),

О

Oto, J to ^ц

Потоки тепла и влаги с поверхности

Т ^х, т), U (х, т)

Волны температуры и влагосодержания

Рис. Обдуваемое воздушным потоком полупространство Fig. Airflow half space недостатком формул Фурье и вытекающих из них законов Фурье, который ограничивает применение содержащихся в них результатов для исследования проблем геокриологии, является то, что они не учитывают наличия в почве влаги, ее перемещения под действием градиентов температуры и влагосодержания и испарения в толще материала и с его поверхности. Исправление этого недостатка и является целью предлагаемой статьи. Применяя теорию тепломассопереноса А.В. Лыкова [8; 12; 13] к задаче для полупространства с периодически изменяющимися граничными условиями, мы получим формулы для асимптотических по времени полей температуры и влагосодержания, в которых движение влаги и ее превращения будут корректно учтены. Такая задача в теории тепло-массопереноса еще никем не рассматривалась.

U ( x , т ). Система уравнений и краевых условий для расчета этих функций будет иметь следующий вид [12; 14]:

дT     d 2 T r у д U  „ = a      +       ; 0 <  x < м ; дт      5 x 2    с дт	(1)
д U     d 2 U    ед 2 T  „ ---= a      + a 5---; 0 <  x <м ; дт m д x 2 m д x 2	(2)
д T / х Q ( т) + г ( 1 -y^ J ( тМ —( 0, т) ; x = 0;	(3)

J ^(т)= a ^{m P} dU ⁽ 0, ^{T) +5d} T ⁽ 0, ^{т) ; x} = ^0;

Q (0 = « w [ ^T ( 0’ т ) - T ] ;

J (Н [ P ( ^{T (0,} 0—Ф P ( T ) ] ;

P ( T ) = 6,03 ■ 10 ^{- 3} exp 173 T .

T + T 1

Соотношения (1) и (2) представляют собой уравнения распространения тепла и влаги в области, занятой материалом; уравнениями (3) и (4) задаются краевые условия на границе x = 0; формулами (5) и (6) определяются интенсивности тепло- и массообмена на этой границе (теплообмен по закону Ньютона и массообмен по закону Дальтона). В приведенных соотношениях: с, р, А, у, am, 5 - теплофизические характеристики материала, а именно – удельная теплоемкость, плотность в сухом состоянии, коэффициент теплопроводности, критерий испарения, коэффициент диффузии влаги, относительный коэффициент термодиффузии влаги; aw = А/(ср) - коэффициент диффузии тепла (коэффициент температуропроводности); г - удельная теплота парообразования воды; aw и am - коэффициенты тепло- и массообмена поверхности образца с воздушной средой; Р(Т) - функция Г.К. Филоненко, моделирующая зависимость относительного парциального давления насыщенного водяного пара от его температуры Т при общем нормальном давлении; Т1 = 238 °С – постоянная.

По причине, о которой будет сказано ниже, вводить в рассмотрение начальные условия для функций Т и U мы не будем.

• 2.    Постановка задачи об асимптотике полей тепломассопереноса

Будем считать, что при т < 0 температура материала и его влагосодержание имели постоянные по всему полупространству значения Т ₀ и U ₀, температура воздуха Т _в равнялась температуре материала Т ₀, а влажность воздуха ф была равна 1. Мы видим, что в таком состоянии система может находиться неограниченно долго, потому что все приведенные выше уравнения оказываются удовлетворенными, причем для интенсивностей тепломассообмена мы будем иметь Q = 0 и J = 0.

Пусть теперь, начиная с момента т = 0, температура воздуха Т _в начинает совершать малые колебания вблизи температуры Т ₀. При малых отклонениях температуры поверхности Т (0, т ) и температуры воздуха Т _в( т ) от фиксированной температуры Т ₀ зависимость (6) можно линеаризовать, разложив функцию Р ( Т ) в ряд Тейлора в окрестности точки Т q . Сделав это и приняв ф = 1, вместо исходной формулы (6) для интенсивности массообмена получим приближенную формулу

J ( т ) = а [ T ( 0, т ) - T ( т ) ] , (7)

dP где at =am dT (T0 )

– коэффициент массообмена по

перепаду температуры .

Представление функции J ( т ) в виде (7) превращает введенную нами систему уравнений в линейную систему, на что в дальнейшем мы будем существенным образом опираться.

Далее будем рассматривать случай, когда малые изменения температуры воздуха происходят по гармоническому закону

T B ( ^т ) = T 0 ^{+ А} T B sin ( ®^{т +} ^ в ) ,

где А T _B, to , v _B — заданные величины. Покажем, что тогда, рассматривая систему (1)–(5), (7), (8), мы можем поставить вопрос о нахождении решения этой системы вида

T ( x , т ) = T q + T ( x ) sin ( toт + v _t ( x ) ) , U ( x , т ) = U ₀ + U ( x ) sin ( toт + v u ( x ) ) ,

в котором и температура, и влагосодержание материала, также как и температура воздуха, совершают при каждом фиксированном x малые гармонические колебания вблизи равновесных значений Т0 и U0. Действительно, вычислив с помощью (9) и (8) разность [T (0, т)- TB (т)] и подставив ее в формулу (7), мы получим:

J ^(т) =

= a t [ T ( 0 ) sin ( toт +v _t ( 0 ) ) — А T _B sin ( toт +v _B )

Таким образом, функция J ( т ) оказывается гармонической. Аналогичным образом, на основании формулы (5), доказывается и гармоничность функции Q ( т ). Но ведь и все другие члены в уравнениях (1)–(4), в соответствии с (9), также будут гармоническими, и потому этим уравнениям можно будет попытаться удовлетворить, подобрав должным образом зависимости

^T ( ^x ) , U ( ^x ) , V t ( ^x ) , V u ( ^x )

в формулах (9). Выполняя такой подбор, которым мы и займемся ниже, мы должны учесть имеющие очевидный физический смысл условия на бесконечности :

T ( x ) ^ 0 и U ( x ) ^ 0 при x ^да . (11)

Сформулированная задача о подборе функций (9) относится к числу задач без начальных данных ; ее решение дает асимптотику полей Т и U при т ^ да .

• 3.    Постановка задачи для комплексов гармонических полей

Искомые функции нашей задачи Т ( x , т ) и U ( x , т ) определяются формулами (9). Введем вместо них новые искомые функции Т *( x , т ) и U *( x , т ) и, обращаясь к методу комплексных амплитуд , сопоставим эти новые функции с их комплексами T ( x ) и U ( x ) по следующим правилам:

' Т * ( x , т ) = Т ( x . т ) - T =

= T ( x ) sin ( toт +v _t ( x ) ) ^ T ( x ) =

_< = ^T ( ^x ) exp ( i v t ( ^x ) ) ;

U * ( ^x , ^т ) = U ( ^x , ^т ) ^- U 0 =

= U ( ^x ) ^sin ( ю^{т +} ^ и ( ^x ) ) o U ( ^x ) =

= U ( x ) exp ( i V u ( x ) ) .

Очевидно, что функции Т* и U* будут удовлетворять тем же уравнениям (1) и (2), что и функции Т и U. Исходя из этого и пользуясь правилами работы с комплексами, вместо указанных уравнений для Т* и U* получим уравнения для комплексов этих функций Т и U:

ito Т (л ) = aw ito и (x ) = a m

dT (x) ry . ' ( \

+ -1 i to U ( л ) ;

dx ² c

d ² U ( л ) dx ²

⁺ a m ⁵

d ² T ( л ) dx ²

Т ( x ) = Т exp ( ц х ) , U ( x ) = U exp ( ц л ) , (16) где Т , U , μ – комплексные постоянные ( метод Эйлера , [15]). Подставляя эти выражения для комплексов в (13), после сокращений получим квадратную систему линейных алгебраических уравнений для нахождения введенных постоянных:

Здесь мы имеем систему двух обыкновенных дифференциальных уравнений второго порядка относительно двух неизвестных комплекснозначных функций действительной переменной. Система линейная, однородная, с постоянными коэффициентами, неопределенная. Для выделения единственного решения этой системы обратимся к оставшимся уравнениям задачи. В области комплексов уравнения (3) и (4) будут выглядеть так:

(2 + - ( 1 -у ) J = Х % ( 0 ) ;

г        dU (гЛ х dT

^J = a m ^P[ И ⁽ 0 ^{) + 5} .. ⁽ 0 )

Образуя комплексы от обеих частей (10) и приравнивая их, с учетом первой из формул (12) получим

^J = « t [ ^Т ( 0 ) -^А Т ] ,

( a w ц ² - i ^to ) ^{Т +}— i ^{to U} = 0;

<^V              ’ c                                            (17)

I a _m 5ц ² T + ( a _m ц ² - i to ) U = 0.

Чтобы решение Т , U этой однородной системы было нетривиальным, ее определитель должен равняться нулю, что приводит к характеристическому уравнению

( a _w ц ² - i to )( a _m ц ² - i to)— ^m— Y i toц ² = 0.         (18)

Это уравнение четвертой степени относительно p, и оно является биквадратным. Раскрывая скобки и вводя новую безразмерную постоянную материала v = 1 f 1 + aw +6-Y У                          (19

• ² 1 a m    c J

  где А Т _в = А Т _в exp ( i у _в ) - заданное комплексное число. Аналогичным образом, обращаясь к формуле (5), для комплекса интенсивности теплообмена будем иметь

  
  

  приведем уравнение (18) к виду

  
  

  ц ⁴

  
  

  2v .    2

  --i toц

  
  

  to

  
  
  
  

  _-

  
  

  = 0.

  
  

  a w a m

  
  

  Q = a w [ ^Т ( ⁰ ) — ^{А Т} в ] ■

  
  

  Вводя новую переменную ^ = ц ² , перепишем это

  
  

  Подставляя полученные выражения для J и Q в (14), после преобразований получим систему двух

  
  

  уравнение так:

  
  

  уравнений следующего вида:

  
  

  ^ ²

  
  

  2 v

  
  

  = 0.

  
  

  a w a m

  
  

  ^Т ( о )

  
  

  е

  - - dT ( 0 ) = а Т ; a _e dx ^х

  
  

  Решая это уравнение, найдем, что

  
  

  ^Т ( 0 ) - О Т dUU ( 0 ) +5: ( 0 ) =А Т в . a t ^ и х         ла

  
  
  
  
  
  

  Л

  
  

  a w

  
  

  —

  
  

  N a m ^v 2

  
  
  
  
  
  

Здесь a _e =a _w + - ( 1 - y ) a _t — эффективная интенсивность теплообмена .

Построив общее решение системы (13), т. е. записав общие выражения для функций Т (л) и U (л), мы затем из системы (15), которая играет роль краевых условий, найдем входящие в эти об- щие выражения произвольные постоянные.

Вспоминая, что ^ = ц , получим в итоге для характеристического уравнения (18) четыре корня

• ^ц 1,2 , 3 , 4 = ±^1,2 ■

Отметим, что в последних двух формулах под z мы понимаем, как обычно, главное значение корня квадратного из комплексного числа z (Re zlz >  0).

Выполним теперь условие на бесконечности (11).

Согласно формулам (16), для их выполнения необходимо иметь Re μ < 0. Следовательно, с учетом свойства главного значения корня, из четырех корней характеристического уравнения нам по- дойдут только два корня ц1 2 =

^-J^ 1 , 2 , ^или

Ц 1 =

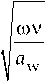
i +

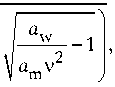
ц ₂ =

—

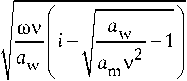
Подставляя эти значения в (15), получим систему линейных алгебраических уравнений для нахождения С _{1 2}:

X             X

I 1 Р 1 I T 1 C 1 + 1 1       ^ 2 I ^T 2 C 2 = ^{А Т} в ^;

V ^а е J k   ^а е    J

Используя найденные корни характеристического уравнения (18), вернемся к системе (17) и найдем коэффициенты Т и U . Поскольку определитель системы равен нулю, уравнения линейно зависимы, и значит, одно из них можно отбросить; оставшееся уравнение будет иметь бесконечно много решений, и потому одно из двух неизвестных можно положить равным любому числу. Имея это в виду, отбросим второе уравнение, а в первом уравнении положим U = 1. Тогда, приняв в этом уравнении сначала ц = р.^ а затем ц = Ц 2 , найдем сначала коэффициент Т ₁, а затем коэффициент Т ₂. Результат будет таким:

<

T 1 —

ci P /     , x

— P1 (1 + 5 T1) C1 + at

a _m P

+ ^T 2 — ^m- ^ 2 ( 1 + ^{5 T} 2 ) ^C 2 = ^A T B *

Определив отсюда С 1 2 и подставив эти коэффициенты в (22), будем иметь решение исходной задачи для комплексов, т. е. решение системы дифференциальных уравнений (13) с краевыми условиями (15). После этого останется только перейти от комплексов к оригиналам, т. е. представить полученные решения в виде (9).

Пример конкретного расчета по указанному алгоритму будет произведен в следующем пункте.

r Y

U = 1; T = —;--------------r i to.

,             ,      c ( i ^{to —} a w Ц 1 , 22 )

Подставляя сюда Ц 1 2 из (20), перепишем после преобразований эти формулы так:

U 1 , 2 = 1; T 1 , 2 = -------------\           •           (21)

^C (1 — v) + i v aw- — 1

⁽      )    4 a v²

m

Определив корни характеристического уравнения μ_{1, 2} и коэффициенты U _{1, 2}, Т _{1, 2}, мы тем самым построили фундаментальную систему решений ( T n exp ( ^ n x ) , U n exp ( ^ n x ) ) , n = 1, ²

для системы дифференциальных уравнений (13). Тогда общее решение этой системы в матричном виде будет выглядеть так:

T (x) ° (x)

= ^C 1 •

T • exp ( p 1 x ) exp ( p 1 x )

⁺ C 2 •

^T 2 • exp ( ^ 2 ^x ) exp ( ^ 2 x )

Здесь μ_{1, 2} вычисляются по формулам (20), Т _{1, 2} – по формулам (21), а С _{1 2} – произвольные постоянные.

Для нахождения постоянных С _{1 2} обратимся к краевым условиям (15). Используя (22), вычислим входящие в (15) величины:

T (0 ) = CT + C2 T2; e dx^ ( 0 ) = C1 T1^1 + C 2 T2^2;

"dx "⁽0 ) = ^C 1 ^ 1 ^{+ C} 2 ^ 2 .

5. Асимптотическое решение для математической модели тепломассопереноса с δ = 0 и γ = 0

Реализация описанного выше расчетного алгоритма представляет собой в общем случае непростую вычислительную работу, сложность которой зависит прежде всего от принятой математической модели тепломассопереноса. Здесь мы ограничимся расчетами в рамках одной из самых простых математических моделей, в которой полагают 5 = 0 (пренебрегают термодиффузией , т. е. движение влаги к поверхности происходит только за счет перепада влагосодержания) и у = 0 (пренебрегают внутренним парообразованием , т. е. превращение воды в пар происходит только на поверхности). Условия применимости такой упрощенной модели к задачам теории тепломассопереноса и анализ получаемых при сделанных приближениях решений можно найти в работах [4-6; 16]. Как видно из (1) и (2), уравнения для температуры и влаго-содержания в этом частном случае оказываются независимыми (связь между функциями Т и U осуществляется в этой модели только через граничные условия), что вносит существенные упрощения в алгоритм исследования процесса, а именно, – отпадает необходимость в использовании теории систем дифференциальных уравнений, на которую мы опирались в предыдущем пункте. Уравнения для комплексов (13) в принявших более простой вид условиях нашей задачи станут такими:

i to T ( X ) = a w

d ² T ( x ) dxx

i to U ( x ) = a m

d ² U ( x ) dx ²

Пользуясь методом Эйлера, найдем общие решения этих уравнений, удовлетворяющие условию на бесконечности (11). Они будут выглядеть так:

T ( x ) = C i exp ( ц 1 x ) , U ( x ) = C 2 exp ( ц ₂ x ) ,         (24)

где

Ц 1 =

—

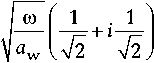
Ц 2 =

—

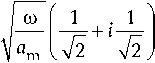
T ( x ) = C 1 exp ( ц 1 x ) =

= I ^C 11 exp ( i arg ^C 1 ) exp P w ( ^{1 +} i ) ^x ] ^

^ C 1 exp ( ^—P w ^x ) sin ( ^{toT +} arg C 1 ^—P w ^x ) .

Основную трудность, как это видно из формул (25) и (26), здесь представляет приведение к показательному виду комплексной постоянной С ₁, т. е. расчет модуля этой постоянной | С 1| и ее аргумента arg C ₁. Проделав такие расчеты и прибавив в соответствии с (12), к получившейся гармонической функции постоянную Т ₀, получим искомое асимптотическое решение для поля температуры:

а С 12 - произвольные постоянные. Для их нахождения воспользуемся краевыми условиями (15). Положив в них 5 = 0 и подставив в получившиеся уравнения найденные выше общие решения T ( x ) и U ( x ) , будем иметь:

C 1 — X С 1 Ц 1/ a e = А Г _в;

C 1 ^— a m P С 2 Ц 2/a _t =^А т ; .

Решая эту систему, после преобразований найдем:

^{А T}„ ^a

^{T ( x} , ^т) = ^T 0 ⁺ /            _{2         2} exp ^(—P w ^{x )х}

N ^(a e ^{+ X}P w ) ^+(XP w )               (28)

х sin

toT + ^B — arctg      w    —Pwx lae +XPw J

C =---^—,

1 — ХЦ 1 уa e

C ₂ = kC 1 ,

Если принять во внимание, как изменяется амплитуда этой синусоиды с изменением координаты x , то станет понятным, почему для величины P w мы применили указанное выше название.

Проделав аналогичные выкладки, для асимпто-

тического поля влагосодержания получим:

a^x где к =----- t .

W a w a m

Итак, решение нашей задачи для комплексов дается формулами (24), в которых коэффициенты определяются формулами (25) и (26). Отметим, что обращение в нуль знаменателя в первой из формул (26) исключено, потому что коэффициент Ц 1 является комплексным.

Теперь мы должны вернуться от комплексов (изображений) к исходным гармоническим функциям времени (оригиналам). В методе комплекс -ных амплитуд этот этап расчетов соответствует нахождению обратного преобразования Фурье при решении задач спектральным методом. Найдем сначала оригинал для комплекса T ( x ) . Введем предварительно новое обозначение. Постоянную μ₁ в формулах (25) запишем в виде

Ц 1 = —P w ( 1 + i ) ,                                      (27)

где P w = ^ «>Д2 a w ) - коэффициент затухания тепловых волн . Обратную величину A w = 1/ P _w назовем глубиной проникновения тепловых волн . Эти названия заимствованы из теории электромагнитных волн. Правомерность обращения к таким терминам будет обоснована ниже. Переход к оригиналу основывается на правиле образования комплексов (12) и осуществляется по следующей схеме:

^U ( x , ^Т ) = ^U 0 ⁺ I       k ^{А T B} ₂ ^a e        ₂ exp ( ^—P m x )

V( a e +^XP w ) + ( ^XP w )

х sin

toT + ^ в

—

arctg

f ^Xp w l^a e ^+XP w J

^— P m ^x

х

Здесь P m =^to/ ( 2 a m ) - коэффициент затухания для волн влагосодержания .

Формулы (28) и (29) и представляют собой решение поставленной в этом пункте частной задачи. Входящие в них коэффициенты затухания P w и P m являются функциями частоты to , а все другие коэффициенты - определенными выше постоянными.

6. Обсуждение результатов

Обсуждение проведем на примере поля температуры. Согласно формуле (28), если температура воздуха, обдувающего влажное полупространство, совершает вблизи фиксированной температуры Т ₀ малые гармонические колебания по закону (8), который характеризуется кроме значения Т ₀ еще и параметрами А T _B, to и ^ _в, то в установившемся режиме колебания температуры вблизи равновесного значения Т ₀ в любом месте полупространства оказываются также гармоническими функциями

времени, причем имеют место следующие закономерности:

• 1)    зависимость амплитуды этих колебаний Δ Т от частоты го и глубины x определяется формулой

A T а

A T = ,            e         exp ( -P w x ) ,

V ( « e +^₽ w ) 2 + ( ^₽ w ) ²

₽ w V ^Ю/ ^{( 2} a w ) ;

• 2)    время запаздывания At максимумов (минимумов) температуры в материале от соответству-

• ющих моментов для температуры воздуха изменяется в зависимости от глубины x следующим образом:

_Л 1 Я ^X₽w   I 1_R

^At = -arctg w   +-P_W ^x .

го      ( «e +xp _w J го

Законы с аналогичной формулировкой могут быть сформулированы и для поля влагосодержания (29).

Сформулированные нами законы изменения во времени полей температуры и влагосодержания в полупространстве с обдуваемой воздухом границей можно рассматривать как обобщение известных в литературе законов Фурье [9; 10], которые справедливы лишь в ситуации, когда, во-первых, материал полупространства не содержит влаги и, значит, рассмотрение ведется только для поля температуры; во-вторых, изменяется по гармоническому закону не температура воздуха, а температура границы полупространства (принимаются граничные условия не 3-го рода, а имеющие ограниченное применение при моделировании процессов тепломассопереноса граничные условия 1-го рода). Этими обстоятельствами существенно ограничивается область использования рассматриваемых в литературе законов Фурье для решения проблем геокриологии.

В статье был рассмотрен гармонический установившийся режим. Используя спектральный метод, предложенный алгоритм расчета можно без труда распространить и на периодические режимы произвольного вида.

В заключительной части статьи в качестве примера мы провели анализ процессов в полупространстве для простейшей модели тепло-массопереноса. Но на основе разработанного в статье алгоритма этот анализ можно применять и к другим типам краевых условий и уравнений распространения тепла и влаги, например, к моделям, используемым в теории двухфазной фильтрации [17].

Развитием предложенных здесь идей может быть построение аналогичных решений не для полупространства, а для пластины. Прохождение гармонических тепловых волн сквозь пластину (важная задача при исследовании теплоизолирующих свойств строительных конструкций) рассмотрена в монографии [7]. Мы планируем обобщить это решение, дополнив тепловые волны волнами влагосодержания. Задача для пластины является актуальной также и в теории электромагнитной сушки, где режимы с периодически изменяющейся интенсивностью излучения используют для организации «щадящих» режимов удаления влаги из термолабильных материалов [4-6]. Исследование таких режимов в теории сушки традиционно производят методом преобразования Лапласа; полученные этим методом решения имеют вид медленно сходящихся рядов и представляют собой для практики в общем случае незначительный интерес, так как с их помощью совсем непросто установить, как влияют на процесс сушки каждый из задающих ее условия параметров в отдельности [4; 13]. Эту проблему интерпретации решений можно устранить, если исключить из расчетов переходные режимы, т. е. начальные периоды сушки, и ограничиться исследованием только установившихся режимов. Правомерность пренебрежения переходными режимами в задачах сушки обосновывалась авторами ранее [18]. Несложно понять, что исследование установившегося режима и интерпретация полученного решения представляют собой намного более простые задачи, чем задачи, возникающие при исследовании процесса на всем его протяжении, включающем переходной режим, и такие расчеты могут быть выполнены по алгоритму настоящей статьи.

Заключение

В рамках теории тепломассопереноса А.В. Лыкова сформулирована краевая задача для расчета полей температуры и влагосодержания в однородном, содержащем влагу полупространстве, граница которого обдувается воздушным потоком. Теплообмен полупространства с воздушной средой происходит по закону Ньютона, а массо-обмен - по закону Дальтона. Методом комплекс -ных амплитуд решена задача об асимптотических распределениях температуры и влагосодержания в условиях, когда температура воздуха изменяется во времени по гармоническому закону. Построенное решение и следующие из него выводы являются обобщениями известных в литературе формул Фурье и законов Фурье, которые относятся к ситуации, когда материал, наполняющий полупространство, не содержит влаги, а по гармо- ническому закону изменяется не температура воздуха, а температура на границе. В рамках полученного общего решения построено частное решение для математической модели тепломассоперено-са, в которой не учитываются термодиффузия и внутреннее парообразование. Результаты работы могут быть использованы в геокриологии в качестве теоретического инструмента при моделировании сезонных колебаний теплофизического со- стояния почвы, что является важной задачей при планировании хозяйственной деятельности в области распространения мерзлых пород.

Финансирование

Исследование выполнено при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-48340015 р_а.