Обобщенное функциональное исчисление в векторных решетках

Пусть E — равномерно полная векторная решетка, x 1 , . . . , x N ∈ E. Изучение непрерывных положительно однородных функций ф : R N ^ R , для которых естественно можно определить ф(х 1 ,..., x n ) G E называем функциональным исчислением. В работе [7] было показано, что естественным образом определяется положительно однородная функция от элементов равномерно полной векторной решетки, если эта функция определена на коническом множестве конечномерного пространства и непрерывна на некотором подконусе последнего.

Цель данной работы — показать, что конструктивным образом можно определить положительно однородную функцию от элементов равномерно полной векторной решетки, если эта функция со значениями в произвольной f -подалгебре идеального центра определена на коническом множестве конечномерного пространства и непрерывна на на некотором его подмножестве. Эта конструкция обобщает аналогичные результаты из [4, 6, 7]. Изучение вышеназванных функций будем называть обобщенным функциональным исчислением . Также рассмотрена связь обобщенного функционального исчисления с двойственностью Минковского, на основе которой доказываются некоторые классические неравенства выпуклости.

2.    Вспомогательные леммы и определение

В этом параграфе дадим определение обобщенного функционального исчисления. Все рассматриваемые векторные решетки предполагаются архимедовыми.

Всюду далее E — равномерно полная векторная решетка, L — векторная подрешетка в E и Л — f -подалгебра в идеальном центре Z (E) с равномерной топологией. Норма

в Z (E) задается формулой ||nk := inf { A > 0 : | n | 6 AI } (n G Л), где I — тождественный оператор на E. Будем предполагать, что L является Л-модулем. Это означает, что пx G L для всех п G Л и x G L. Обозначим через Hom(L) и H _m (Л), соответственно, множество всех R -значных решеточных гомоморфизмов на L и множество всех R -значных мультипликативных решеточных гомоморфизмов на Л.

Следующая лемма играет важную роль при построении обобщенного функционального исчисления.

Лемма 2.1. Для любого ш G Hom(L) существует единственный ш G Н _т (Л) такой, что | ш | 6 1 , ш(пx) = Ш(п)ш(x) для всех п G Л и x G L. При этом Аш = ш для всех 0 < A G R и ш G Hom(L) .

C Если ш G Hom(L) равен нулю, то полагая ш(п) = 0 для всех п G Л, получим требуемое. Пусть 0 = ш G Hom(L). Билинейное отображение b : Л х L ^ R, действующее по формуле Ь(п, x) := ш(пx) для всех п G Л и x G L, является решеточным биморфизмом. Согласно [1, теорема 3.2] существуют решеточные гомоморфизмы S : Л ^ R и T : L ^ R такие, что ш(пx) = S(п) T(x) (1)

для всех п G Л и x G L. Взяв в качестве п тождественный оператор I на E , получим ш(x) = S (I)T(x). Отсюда, ввиду 0 = ш следует S (I) > 0 и T (x) = аш(x), где а = S (I) ^{- 1} . Положим по определению ш(п) := аS(п) для всех п G Л. Тогда из равенства T (x) = aш(x) и формулы (1) следует ш(пx) = S(п)аш(x) = Ш(п)ш(x) для всех п G Л и x G L. Покажем мультипликативность гомоморфизма ш. Пусть п,р G Л. Тогда ш((пp)x) = ш(пp)ш(x) для всех x G L. С другой стороны ш((пp)x) = ш(п(px)) = ш(п)ш(px) = ш(п)ш(p)ш(x) для всех x G L. Поскольку 0 = ш, выполняется равенство ш(пр) = ш (п)ш(р). Единственность ш также следует из равенства ш(пx) = ш(п)ш(x) для всех п G Л и x G L.

Покажем, что Аш = ш для всех 0 < A G R и ш G Hom(L). Предположим, что решеточный гомоморфизм ш G Hom(L) отличен от нуля, так как в противном случае доказывать нечего. Тогда Аш G Hom(L) и в силу определения Аш выполняются равенства Aш(пx) = Aш(п)Aш(x) = Aш(п)ш(Ax) для всех п G Л и x G L. С другой стороны, Aш(пx) = A(ш(пx)) = Aш(п)ш(x) = Ш(п)ш(Ax) для всех п G Л и x G L. Из условий ш = 0 и А > 0 выводим Аш = ш. Соотношение | ш | 6 1 следует из того, что ш (I ) = 1, а единичный шар в Л совпадает с порядковым интервалом [ — I, I]. B

Пусть x i ,..., x n G E не равны нулю одновременно. Символом Л h x _i ,..., x n i обозначим Л-модульную подрешетку в E, порожденную набором x := (x i ,..., x n ). Положим по определению

Л[ х ] := Л[x ₁ ,...,x _N ] := {(ш(x ₁ ),...,ш(x _N )) : 0 = ш G Hom(Л h x _i ,...,x _N i )}.

Лемма 2.2. Пусть S := { t G R N : | t 1 | + ... + | t _N | = 1 } , u := | x _i | + ... + | x _N | , Q := { ш G Hom(Л h x ₁ ,..., x n i ), ш(и) = 1 } и Q(x i ,..., x n ) := { (ш(x ₁ ),..., ш(x N )) : ш G Q } . Тогда Q(x i ,..., x n ) компактное множество в R N , S П Л[x 1 ,..., x n ] = Q(x i ,..., x n ) и Л[X 1 ,...,X N ] = U{AQ(x i ,...,X N ) :0 <А G R } .

C В силу того, что для каждого гомоморфизма ш G Hom(Л h x _i , ...,x n i ) выполняется равенство | ш(x i ) | + ... + | ш(x N ) | = ш(и) следует справедливость формулы S П Л[x _i ,..., x n ] = Q(x _i ,..., x n ). Проверим компактность Q(x _i ,..., x n ) в R N . Обозначим через L := Л h x i ,..., x n i и снабдим Q топологией, индуцируемой из R L . Тогда Q является компактным множеством в R L . В самом деле, замкнутость Q в R L очевидна.

Так как u сильная порядковая единица в L, то для каждого x ∈ L найдется такое число ^ x >  0, что | x | 6 ^ x u. Поэтому Q C II_xGl [— ^ x , ^ x ]. По теореме Тихонова П _xGl [— ^ x ,M x ] является компактным множеством в R L . Следовательно, Q является замкнутым подмножеством компактного множества. Заметим, что Q(x i ..., x n ) служит образом Q при непрерывном отображении ш ^ (ш(x ₁ ),..., ш(x N )) из R L в R N . Поэтому Q(x i ,..., x n ) — компактное множество в R ^N .

Справедливость формулы Л[x 1 ,..., x n ] = [J{AQ(x i ..., x n ) : 0 < A G R } следует из равенства Hom(Л h x ₁ ,..., x n i ) \ { 0 } = S { AQ : 0 < A G R } . B

Множество C C R N называется коническим, если AC C C для всех A > 0. Функция ^ : C ^ Л, заданная на коническом множестве C, называется положительно однородной, если ^(At) = A^(t) для всех A > 0 и t G C.

Пусть коническое множество C C R N содержит K. Символом H (C, K, Л) будем обозначать векторную решетку, состоящую из всех положительно однородных функций у : C ^ Л, непрерывных на K.

Определение 2.1. Пусть E — равномерно полная векторная решетка, Х 1 ,..., x n , y G E, Л — f-подалгебра в Z (E). Предположим, что K содержит ЛХ..., x n ] и ^ G H (C, K, Л). Будем писать у = ^, x i , ...,x n ), если выполняется равенство ш(у) = Ш(y(ш(x ₁ ),..., ш(x N ))) для всех ш G Hom(Л h x ₁ ,..., x n , y i ).

Всюду далее в этом параграфе будем предполагать, что x 1 , . . . , x N , y ∈ E и ϕ ∈ H(C, K, Л).

Лемма 2.3. Пусть у = ^( - , X i ,..., x n ) , L — некоторая Л-модульная подрешетка в E , содержащая у, X i ,..., x n . Тогда ш(у) = ш(y(ш(x ₁ ),..., ш(x N ))) для всех ш G Hom(L) .

C Пусть ш G Hom(L). Обозначим через ш ⁰ сужение ш на Л h x 1 ..., x n , y i . Предположим сначала, что ш(x _i ) = 0 для всех i = 1,..., N. Тогда ^(ш(х^),..., ш(x N )) = 0 и справедливы равенства ш(у) = ш ⁰ (у) = ш ⁰ (^(ш ⁰ (х ₁ ),..., ш ⁰ (x n ))) = ш ⁰ (^(ш(х ₁ ),..., ш(x N ))) = 0 = ш(^(ш(х ₁ ),...,ш(x N ))). Пусть теперь ш(х ^ ) = 0 для некоторого j G { 1,...,N } . Тогда в силу леммы 2.2 выполняются равенства ш(п)ш(х ^ ) = ш(пх ^ ) = ш ⁰ (пх ^ ) = ш ⁰ (п)ш ⁰ (х ^ ) = ш ⁰ (п)ш(х ^ ) для всех п G Л, поэтому ш = ш ⁰ . Следовательно, ш(у) = ш ⁰ (у) = ш ⁰ (^(ш ⁰ (х ₁ ),..., ш ⁰ (x _N ))) = ш(^(ш(х ₁ ),..., ш(x _N ))). B

Лемма 2.4. Существует единственный элемент у G E такой, что у = ^( - , х ₁ ,..., x n ) .

C Предположим, что для некоторых у, У 1 G E выполняются у = ^, x i , ...,x n ) и y ₁ = ^( - , x i ,..., x n ). Обозначим через L := Л h x ₁ , ...,x n , у,у^. В силу леммы 2.3 справедливы равенства ш(у) = ш(y(ш(x _i ),...,ш(x N ))) = ш(y _i ) для всех ш G Hom(L). Поскольку в L имеется сильная порядковая единица, то по теореме Крейнов — Какутани L C C(Q), где Q — подходящий компакт. Следовательно, Hom(L) различает точки из L, что влечет справедливость леммы. B

Лемма 2.5. Пусть подмножество G C Hom(Л ( x 1 ,..., x n , y i ) различает точки из Л h x i ,...,X N , y i . Если для всех ш G G выполняется равенство ш(у) = w(y^(x i ),... ,ш(x N ))) , то у = ^( - ,X i ,... ,x n ) .

C Введем обозначения u := | x i | + ... + |x n | + | у | , L := Л h x ₁ ,..., x n , y i , Q := { ш G Hom(L) : ш(и) = 1 } и Q 0 := Q П G. Так как Hom(L) \ { 0 } = S { AQ : 0 < A G R } , то в силу леммы 2.1 и положительной однородности у достаточно установить ш(у) = ш(y(ш(x ₁ ),..., ш(x N ))) для всех ш G Q. По условию леммы Q 0 различает точки из L, и для всех ш G Q 0 справедливо равенство

ш(у) = ш(y(ш(x 1 ),... ,ш(xN))).

Снабдим 9 топологией поточечной сходимости, индуцируемой из R L . Тогда 9 замкнуто в R L и L является векторной подрешеткой в C (9). Так как и сильная порядковая единица в L, то для каждого x G L найдется такое число ц _х >  0, что | x | 6 ^ x u. Поэтому 9 С П _X£l [— M x , M x ]- По теореме Тихонова H_xgl [— M x , M x ] является компактным множеством в R L . Следовательно, 9 — компактное множество. По теореме Вейерштрасса L плотна по норме в C(9). Поэтому в силу [5, лемма 1.2] L порядково плотна в C(9). Отсюда вытекает плотность множества 9 0 в 9. Действительно, если это не так, то по лемме Урысона существует ненулевая функция x : 9 ^ [0,1], обращающаяся в нуль на 9 0 . В силу порядковой плотности L в C(9) подберем x g G L + так, чтобы 0 = x g 6 | x | . Тогда ш(x g ) = 0 для всех ш G 9 0 , что противоречит условию 9 0 различает точки из L.

Покажем, что для произвольного ш G 9 выполняется равенство (2). Возьмем сеть (ш _а ) С 9 0 , сходящуюся к ш. Тогда ш _а (пx) ^ ш(пx) для всех п G Л и x G L. Полагая в этом соотношении x = и, ввиду леммы 2.1 получим ш _а (п) ^ ш(п) для всех п G Л. Полагая п = I , из последнего соотношения вытекает

||Ш а - ш | ^ 0.

Если ш( | x 1 | +... + |x n | ) = 0, то ввиду формулы (3), непрерывности у и леммы 2.1 следует справедливость соотношений

| Ш а (^(Ш а (x i ), . . .,Ш a (x N ))) - Ш^Ш^ т ), . . . ,ш(x N ))) | 6 ^| Ш a (y(Ш a (X 1 ), . . . ,Ш а (x n ))) - W а (ю(ш(x 1 ), . . . ,ш(x N ))) + ^| Ш a (y(ш(X 1 ), . . . , Ш(X N ))) - w(^(x i ), . . . , ш(x N ))) ¹

6 ||y(Ш a (X 1 ), . . .,Ш a (x N )) - ^(ш(X 1 ), . . . ,ш(x N ))|| + ^Ш а — Ш^ ^||y(ш(X 1 ), . . . , ш(x N )) || ^ 0.

Мы получили, что ш _а (у) ^ Ш(y(ш(x 1 ),..., ш(x N ))). С другой стороны, по определению топологии на 9 верно ш _а (у) ^ ш(у), поэтому ш(у) = w(^(w(x i ),..., ш(x N ))).

Покажем, что ш( | x 1 | + ... + |x n | ) не может равняться нулю. В самом деле, если ш( | x ₁ | + ... + |x n | ) = 0, то ш( | у | ) = ш(и) = 1. Поэтому для любого 0 < е < 1 найдется индекс а д такой, что ш _а (у) > 1 — е для всех а > а д . Отсюда, ввиду формулы (2) ш _а (^(ш _а (x i ),..., ш _а (x n ))) > 1 — е, что влечет ш _а ( | x ₁ 1 + ... + |x n | ) = 0 для всех а > а д . Обозначим через x g := | x _i | + ... + |x n | . Тогда в силу положительной однородности у выполняются соотношения

1 — е < Ш а (у) = Ш а (^(Ш а (x i ), . . . ,Ш а (x N )))

Ш а (x g ) Ш а

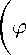
/ Ш а (X 1 )      Ш а (x N )

VШ а (x g ) ’ . . . ’ Ш а (x g )

для всех а > а д . Так как ю непрерывная функция и ( ^{Ш а ( х} 1 ) ,.    ^( x N ) j g S : = {t G

\ ^a \ ^x 0 )          ^ а \^х 0 ) j                I

RN : |ti| + ... + |tN| = 1}, то из компактности S и формулы (4) следует существование числа M > 0, удовлетворяющего неравенству

1 — е < Ш а (у) 6 M • Ш а (x g )

для всех а > а д . Переход к пределу в последнем неравенстве влечет 1 — е 6 Mш(x g ) = 0 — противоречие. Следовательно, формула (2) справедлива для всех ш G 9. B

Лемма 2.6. Пусть L _i — Л -модульная подрешетка в E , x i ,..., x n , y G L _i и Hom(L _i ) различает точки из L i . Если равенство ш(у) = Ш(ю(ш(x 1 )’..., ш(x N ))) выполняется для всех ш G L _t , то y = ^( ’ , x i , • • •, x n ) .

C Пусть L := Л h x ₁ ,..., x n , y i . Обозначим через G := {ш^ : ш E Hom(L ₁ ) } . Тогда G разделяет точки из L и справедливо равенство ш(у) = w(y(ш(x 1 ),..., ш(x N ))) для всех ш E G. По лемме 2.5 y = у ( • , x ₁ ,..., x n ). B

3.    Основной результат

Далее мы сформулируем результат, в котором устанавливается Л-модульный гомоморфизм из класса H(C, K, Л) в E. Образ этого гомоморфизма равномерно замкнут и конечно порожден, если f -подалгебра Л замкнута по норме.

Обозначим символом F ( • , х ) множество всех функций у E H(C, K, Л), для которых существует у( ^ , x 1 ,...,X N ) E E .В силу леммы 2.4 существует отображение b : у ^ у( ^ , x 1 ,... ,x n ) из F ( • , х ) в E . В векторной решетке H (C, K, Л) введем структуру модуля над кольцом Л следующим образом:

⁽ⁿ^^{)(t) :}= ^п ◦ y^(t), ⁽⁵⁾

где п E Л, у E H (C, K, Л), t = (t ₁ ,...,t _N ) E C . Введем функции dt i E H (C, K, Л) (1 6 i 6 N ) по формуле dt i (t) = t i l , где t = (t ₁ , ...,t N ) E R N . Обозначим через e := | dt i | +... + | dt N | E H (C, K, Л). Из положительной однородности следует H (C, K, Л) е-равномерно полно и e(t) = \\t\\I для всех t E R N .

Определение 3.1. Пусть E, F — векторные решетки, Л, Л ⁰ — f -подалгебры соответственно в Z(E ) и Z (F), । : Л ^ Л ⁰ — мультипликативный порядковый изоморфизм. Будем говорить, что решеточный гомоморфизм h : E ^ F Л-модульный, если выполняется равенство h(пx) = lп(hx) для всех п E Л и x E E . При отождествлении Л с Л ⁰ будем писать h(пx) = п(hx) для всех п E Л и x E E .

Лемма 3.1. Множество F ( • , х ) является Л-модульной решеткой и отображение b : у ^ у (> x ₁ ,..., x n ) является Л-модульным решеточным гомоморфизмом из F ( • , х ) в E таким, что b(dt i ) = x i для всех i = 1,2,..., N .

C Возьмем У 1 ,У 2 E F ( • , х ), и пусть У 1 = У 1 ( ^ ,Х 1 , ...,x N ) и У 2 = у 2 ( • ,x i , ...,x n ). Обозначим через L := A ( x 1 ,..., x n , У 1 , y 2 i . В силу леммы 2.3 для всех ш E Hom(L) справедливы равенства ш(у ₁ ) = ш(^ 1 (ш(x ₁ ),..., ш(x N ))) и ш(у ₂ ) = w(y ₂ (ш(x ₁ ),..., ш(x N ))). Складывая эти равенства, получим ш(у ₁ + y ₂ ) = ш[(у ₁ + У 2 )(ш(х 1 ),...,ш(x N ))] для всех ш E Hom(L). Отсюда, в силу леммы 2.6 y 1 + у 2 = (у 1 + у 2 )( • ,x 1 ,..., x n ). Аналогично можно показать b(y 1 V ^ 2 ) = b(y ₁ ) V b(y ₂ ) и b(Ay ₁ ) = Ab(y ₁ ) (A E R ). Докажем, что b Л-модульный гомоморфизм. Возьмем п E Л, у E F( • , х ) и пусть y = b(y). В силу мультипликативности ш имеем ш(пу) = ш(п) • ш(у) = ш(п) • Ш(y(ш(x ₁ ),...,ш(x N ))) = ш[(пy)(ш(x ₁ ),..., ш(x N ))] для всех ш E Hom(Л h x ₁ ,..., x n , y i ). Следовательно, применив лемму 2.6, получим пу = (пy)( • ,x ₁ ,... ,x n ), что означает п( Ь (^)) = Ь (пу) . B

Лемма 3.2. Л-модульная решетка F ( • , х ) е -равномерно замкнута в H (C, K, Л) , где е = | dt 1 | + ... + | dt N | .

C Пусть последовательность (yn)neN из F(•, х) сходится к у E H(C, K, Л) с регулятором е. Тогда yn := b(yn) (n E N) будет r-фундаментальной последовательностью в E с регулятором u := b(e) = |x11 + ... + |xn|. В силу полноты E существует y E E такой, что yn → y с регулятором u. Пусть L обозначает идеал в E , порожденный элементом |y| + u. Тогда последовательность (yn)neN содержится в L и Hom(L) различает точки из L. Для каждого ш E Hom(L) выполняется ш(уп) ^ ш(у). В свою очередь, в силу леммы 2.3 ш(уп) = ш(yn(ш(x1),..., ш(xN))) для всех n E N, и так как yn ^ у в каждой точке из конического множества C, то ш(уп(ш(x1),..., ш(xN))) ^ ш(у(ш(x1),..., ш(xN))). Таким образом, ш(у) = ш(у(ш(x1),...,ш(xN))) для всех ш Е Hom(L). В силу леммы 2.6 y = у(> xi,... ,xn), т. е. у Е F(•,х). B

Теорема 3.1. Пусть E — равномерно полная векторная решетка, Л — f -подалгебра в Z(E ) , x i ,...,x n Е E . Предположим, что K С R N содержит Л[x 1 , ...,x N ] . Тогда отображение b : у ^ у( • ,X 1 ,...,x n ) единственный Л-модульный решеточный гомоморфизм из H (C, K, Л) в E такой, что b(dt i ) = x i (1 6 i 6 N ) . Более того, b(H(C, K, Л)) содержится в u-равномерном замыкании Л-модульной подрешетки, порожденной x ₁ ,..., x n , т.е. b(H(C, K, Л)) С Л ( х 1 ,..., x n i, где замыкание вычисляется в E равномерно относительно u = | x i | + ... + |x n | . Если Л замкнута по норме в Z(E ) , то b(H (C, K, Л)) = A ( x 1 ,...,x N ) .

C Предположим сначала, что K = Л[ х ] и C = Л[ х ] U { 0 } . Пусть F n является Л-модульной подрешеткой в H(C, K, Л), порожденная функциями dt i ,... ,dt N , т. е. F n : = Лhdt ₁ ,... ,dt N } . Покажем, что гомоморфизм b : F( • , х ) ^ E из леммы 3.1 распространяется на H(C, K, Л). Для этого в силу леммы 3.2 и соотношения F n С F ( • , х ) достаточно доказать e-равномерную плотность F n в H(C, K, Л), где e = | dt i | +.. . + | dt N | .

По лемме 2.2 множество P := Л[x1,..., xn] П S, где S := {t Е RN : ||t| = 1}, компактно в RN. Ввиду положительной однородности каждая функция из H(C, K, Л) однозначно определяется своими значениями на P. Поэтому H(C, K, Л) отождествляется с C(P,Л). В силу [5, предложение 2.1] существует компакт Q и решеточный изоморфизм ст из Л на плотную по норме векторную подрешетку в C(Q), при котором мультипликативная единица I Е Л переходит в тождественную единицу 1q. Отсюда в силу [3, теорема 2.58] выполняется равенство ст(П1 О П2) = ст(П1) • ст(п2) (6)

для всех П 1 ,П 2 Е Л. Построим отображение v : C(P, Л) ^ C(P х Q) по формуле v(у)(p, q) := ст(у(p))(q) для всех (p, q) Е P х Q. Тогда v является инъективным решеточным гомоморфизмом, и ввиду формулы (6) выполняется равенство

v(пу)(p, q) = ст(п)(q) • v(у)(p, q) (7)

для всех п Е Л, у Е C(P, Л) и (p, q) Е P х Q. Так как v(e) есть тождественная единица на P х Q, то e-равномерная плотность F n в C(P, Л) следует из плотности по норме v (F n ) в C(P х Q). Покажем, что v (F n ) удовлетворяет всем требованиям теоремы Стоуна — Вейерштрасса (см., например, [10, теорема 2.1.1]). Так как e = | dt 1 1 + ... + | dt N | Е F n и v(e) = 1 р _xq следует v (F n ) содержит константы. Пусть (p, q ₁ ), (t,q ₂ ) Е P х Q. Если p = t, то p j = t j для некоторого j Е { 1,... , N } . Тогда ввиду ст(1) = 1 q выполняются равенства v(dt j )(t, q ₁ ) = ст(t j I)(q ₁ ) = t j = p j = v(dt j )(p, q ₂ ). Если q ₁ = q ₂ , то ввиду плотности ст(Л) в C(Q) найдется элемент п Е Л такой, что ст(п)(q 1 ) = ст(п)^). Тогда в силу (7) будут справедливы соотношения v(ne)(t,q ₁ ) = ст(п)(q ₁ ) • 1 = ст(п)(q ₂ ) = v(ne)(t,q ₂ ). Мы получили, что v (F n ) удовлетворяет всем требованиям теоремы Стоуна — Вейерштрасса, поэтому v (F n ) плотна по норме в C(P х Q), что влечет e-равномерную плотность F n в C(P, Л). Таким образом, F( • , х ) = H(C, K, Л). Равномерная плотность F n в C(P, Л) также влечет b(H(C, K, Л)) С Л h x ₁ ,..., x n i .

Покажем единственность гомоморфизма b Пусть T : H (C, K, Л) ^ E — Л-модульный решеточный гомоморфизм и T (dt i ) = x i для всех i = 1, 2,... , N. Тогда множество G := { у Е F n : Ь (у) = T(у) } является Л-модульной подрешеткой в F n , содержащей dt i (1 6 i 6 N). Следовательно, F n = G ив силу плотности F n в H (C, K, Л) получим T = b

Покажем справедливость равенства b(H (C, K, Л)) = Л ( x ₁ , ...,x n i при условии, что Л замкнута по норме в Z (E). Включение С установлена выше. Так как образ b(H(C, K, Л)) содержит х 1 ..., x n , является модулем над Л и равномерно полон (см. [9, теорема 59.3]), то b(H(C, K, Л)) D Л ( x 1 ,..., x n i . Таким образом, мы доказали теорему для C = Л[ х ] U { 0 } .

Возьмем теперь произвольное коническое множество C С R N , содержащее K . Обозначим через C 1 := Л[ х ] U{ 0 } . Оператор сужения р : у ^ v\c 1 осуществляет Л-модульный решеточный гомоморфизм из H(C, K, Л) в H(C, Л[ х ], Л). Поэтому, b о р — требуемый Л-модульный гомоморфизм. B

Предложение 3.1. Пусть E, F — равномерно полные векторные решетки, i : Л ^ Л ⁰ — изоморфизм f -алгебр Л С Z(E ) и Л' С Z (F) , h : E ^ F — Л-модульный решеточный гомоморфизм. Предположим, что x 1 ,...,x N Е E , Л[x ₁ ,...,X N ] С K и у Е H (C, K, Л) . Тогда Л ' [h(x 1 ),..., h(x N )] С A[x 1 ,..., x n ] и справедливо равенство

h(^, 1 ,... ,x n )) = i о ^( - , h(x i ),..., h(x N )). (8)

C Положим y i := h(x i ) (i = 1,...,N), u := \ x 1 \ + ... + \x n | . Возьмем 0 = ш Е Нош(Л ' (у ₁ , ...,y N i ). Тогда ш := ш о h е Hoш(Л ( x ₁ ,...,x N i ) и поэтому Л ' [h(x ₁ ),..., h(x N )] С Л[x ₁ ,..., x n ]. Отсюда видно, что i о ^ е H(C, K, Л ' ).

Предположим, что h(u) = 0. Тогда в силу теоремы 3.1 ^( - ,x i , ...,x n ) принадлежит главному идеалу E _u в E, порожденному элементом u. Следовательно, h(^( - , x i , ...,x n )) = 0. С другой стороны, hx = 0 для всех i = 1,...,N, поэтому i о ^( - , h(x 1 ),..., h(x _N )) = 0.

Пусть h(u) = 0. Из леммы 2.1 известно, что ш Е Н _т (Л ⁰ ) и w = ш о h е Н _т (Л). Покажем, что w(in) = ш(п) для всех п Е Л. Действительно, пусть п Е Л. Тогда по лемме 2.1 ш(lп(hu)) = Ш(lп)ш(hu) = Ш(lп)ш(u). С другой стороны, в силу Л-модульности h следует ш(lп(hu)) = ш(h(пu)) = ш(пи) = ш(п)ш(и). Отсюда, так как cW(u) = 0, выводим

w(in) = ш(п) (п Е Л). (9)

Положим x := у( - , x i ,... ,x n ), y := i о ^( . , y_b... ,y N ), и пусть ш Е Hoш(A ⁰ ( y,y 1 ,... ,y N > ). Тогда ш := ш о h е Hoш(Л ( x,X 1 , ...,x n i ), и ввиду (9) выполняются равенства ш(у) = w(i о у(ш(у 1 ),..., ш(y N ))) = Ш(y(Ш(x ₁ ),..., lD(x n ))) = ш(x) = ш(hx). Следовательно, так как Hoш(A ⁰ ( y,y 1 ,..., y N i ) различает точки, y = h(x). B

Замечание 3.1. В условиях предложения 3.1 при отождествлении Л с Л ' формула (8) примет вид h(^(> x 1 ,..., x n )) = ^( - , h(x 1 ),..., h(x N )).

4.    Метод огибающих

В этом параграфе покажем, что обобщенное функциональное исчисление позволяет перенести двойственность Минковского на Л-модульные решетки.

Пусть E — равномерно полная векторная решетка, x 1 ,..., x n Е E, Л — f-подалгебра в Z (E), K — замкнутый конус в R N , содержащий Л[x 1 ,...,X N ]. Обозначим через H v (K, Л) (H ^ (K, Л)) множество всех сублинейных (суперлинейных) непрерывных операторов из K в Л, L( R N , Л) — пространство линейных операторов из R N в Л. Пусть ( п, •i обозначает линейный оператор t ^ ( п, t i = P N=1 t _i п _i из R N в Л, где t = (t 1 ,..., t N ) Е R N , п = (п..., П N ) Е Л ^N . Ясно, что отображение п ^ ( п, •i осуществляет решеточный изоморфизм из Л ^N на L( R N ,Л).

Для сублинейного оператора у : K ^ Л U {+^} (суперлинейного оператора ф : K ^ Л U {-го}) положим по определению ду : = {п Е ЛN : h', ti 6 y(t) (t Е K)},

дф := {п Е Л ^N : ( п,^ >  y(t) (t Е K)}.

Следующая лемма используется в доказательстве основного результата параграфа. Заметим, что если Q — компакт и Л С Z (C(Q)), то в силу [3, теорема 2.62] Л С C(Q).

Лемма 4.1. Пусть Q — произвольный компакт, x i , ...,x n Е C (Q) , Л С C (Q) , Л[x ₁ ,...,X N ] С K и у Е H (C, K, Л) . Тогда у( - , x i , ...,x n ) Е C (Q) и справедливо равенство у( - , x _i ,..., x n )(q) = y(x _i (q),..., x n (q))(q) для всех q Е Q.

• <1 Пусть E u обозначает порядковый идеал в C (Q), порожденный элементом u : = | x i | +... + |x n | . Тогда E u равномерно замкнут в C (Q) относительно u и является модулем над Л (см. [3, теорема 2.62]). Поэтому из теоремы 3.1 получим у( - , x 1 ,..., x n ) Е E u .

Всякий элемент q Е Q отождествляется с решеточным гомоморфизмом ш _q Е Hom(E u ) по формуле ш _q (x) := x(q) (x Е E u ). Пусть q Е Q и u(q) = 0. Тогда из леммы 2.1 выводим n(q)u(q) = ш _q (пи) = f q (n)u(q) для всех п Е Л. Сократив на u(q), получим n(q) = f q (п) (п Е Л). Отсюда из определения у( - , x _i ,..., x n ) следует у( - , x _i ,..., x n )(q) = f q (у(> x i ,.. .,x n )) = Ш у (y(f q (x i ),..., f q (x n )) = y(x i (q),..., x n (q))(q).

Пусть теперь u(q) = 0. Тогда x(q) = 0 для всех x Е E _u . В частности, у( - , x i ,..., x n )(q) = 0. С другой стороны, ввиду положительной однородности у следует 0 = y(x _i (q), ..., x _N (q))(q). Таким образом, у( - , x _i ,..., x _N )(q) = y(x _i (q), ..., x _N (q))(q) для всех q Е Q. B

Теорема 4.1. Пусть E — равномерно полная векторная решетка, x _i ,... , x n Е E, у Е H ^ (K, Л) и ф Е Н д (К, Л) . Тогда справедливы равенства