Обобщенное интегро-дифференциальное неравенство Виртингера

Интегро-дифференциальные неравенства, связывающие интегралы от функции и ее производных, давно привлекали внимание исследователей. Одним из наиболее известных является классическое неравенство Виртингера

2 п             2 п

| x 2( t) dt > | x 2( t) dt, справедливое для всех таких функций, что 2п

| x ( t ) dt = 0. Хорошо известно также анало- 0

гичное неравенство bb

| x&(t ) dt >  у | x ²( t ) dt             (1)

aa для функций с условием x(a) = 0. Оно спра-

”

ведливо при всех у <  у = ------у . Константа

4( b - a)²

у здесь точная, т. е. не может быть увеличена. Позднее Левин [1] при целых m >-2 нашел точную константу для более общего неравенства bb

| ;&( t ) dt >  у | ( t - a ) ^mx ²( t ) dt .

aa

Для интегро-дифференциального неравенства вида bb

| x 2 ( t ) dt >  у | | x & t ) x ( t )| dt        (2)

aa с условием  x (a) = 0 точная константа

У =7— b - a

Для неравенства (1) и функций с условиями на концах промежутка x ( a ) = x ( b ) = 0,

п2     « a « наилучшая константа у = —--— может быть получена, например, методами классического вариационного исчисления. Для неравенства (2) с этими условиями наилучшая константа 4

у =---- была найдена в работах [3,4].

b - a

В работе Troy [5] получены оценки у, при которых выполняется более общее неравенство bb

| x 2 ( t ) dt >  у | t^p\x& ) x ( t )| dt        (3)

aa при условии x(a) = 0 (а также при условиях x (a) = x (b) = 0), и поставлен вопрос о точности найденных констант.

aa обобщающему неравенства, рассмотренные ранее в работах [1–5]. В ней получены достаточные условия справедливости неравенства (4), а в некоторых случаях, в том числе для неравенства (3), получены точные оценки.

Применяемые ниже методы основаны на редукции интегро-дифференциального неравенства (4) к задаче минимизации квадратичного функционала b

J ( z ) = j ( z ( t ) - ( Kz )( t ) ) z ( t ) dt ^ min . a

Функционал J рассматривается в гильбертовом пространстве     L₂     функций

z :[ a , b ] ^ R , суммируемых с квадратом на промежутке [ a , b ]. Линейный интегральный оператор K : L ₂ ^ L₂ является самосопряженным и ограниченным. Ясно, что либо минимум функционала J равен нулю и достигается на решениях уравнения z = Kz , либо функционал J на множестве L неограничен снизу. Как известно, минимум функционала J равен нулю, если, и только если, все точки спектра оператора K не превосходят единицы. Всюду ниже в качестве оператора K выступают интегральные операторы с неотрицательным ядром. В этом случае минимум существует тогда и только тогда, когда норма (спектральный радиус) оператора K не превосходит единицу [11] .

Отметим сразу, что вычислить норму (спектральный радиус) этих интегральных операторов удается в исключительных случаях. Однако эти случаи представляют особый интерес, именно они позволяют получать точные условия справедливости неравенства (4).

• 1.    Неравенство с условием x ( a ) = 0

Пусть функции p, q :[a, b] ^ R измеримы и неотрицательны на [a, b], причем bb        (        b        ^2

J ( t - a ) p ( t ) + qq ( s ) ds a       i t         )

dt <^ .

Множество

Отметим прежде всего то, что на пространстве W функционал

b

равенством

b

J ( x ) = j ( x &( t ) - 2 p ( t ) x& ) x ( t ) - q ( t ) x ²( t ) ) dt .

a

Лемма 1.1 . Неравенство (4) справедливо для каждого x g W_a тогда и только тогда, когда решением вариационной задачи

J ( x ) ^ min, x ( a ) = 0,

является нулевая функция x = 0 .

Доказательство. Если x = 0 не является решением задачи (5), то функционал J отрицателен для некоторой функции x₀ g W_a . Так как I ( x ₀) <  J ( x ₀) <  0, то неравенство (4) не выполнено для функции x .

J ( x ₂) = I ( x ₂) <  I ( x ) <  0.

Обозначим через

b

⁽ K b z ⁾⁽ t ) = j Kb ⁽ t , s ) z ⁽ s ) ds

a интегральный оператор с симметричным и неотрицательным ядром b

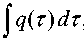
K b ( t , s ) = t

t

b

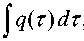
a < s < t < b, a < t < s < b.

Оператор K : L ^ L ограничен вполне непрерывен, так как

и

b

vraisup p ( t ) + J q ( s ) ds <  l ^ [ a , b ] I                ,               )

t

b - a ’

b

||K b ||²<  2 J ( t - a ) p ( t ) + a        I

b

t

Ж .

Теорема 1.1 . Неравенство (4) справедливо для всех x е W_a тогда и только тогда, когда || K _b 11 < 1 .

Доказательство. Задачу (5) подста-t новка x(t) = J z(s) ds редуцирует к задаче a b

J ( z ( t ) - ( K_bz )( t )) z ( t ) dt ^ min . a

Следовательно, задача (5) разрешима тогда и только тогда, когда \\К_Ь || < 1 . Но в силу леммы 1.1 это условие эквивалентно справедливости неравенства (4) при всех x е W_a . Оценивая норму оператора K , получаем

Следствие 1.1. Если

то неравенство (4) справедливо для всех x ^{е W} a .

Вышеприведенные следствия определяют достаточные условия справедливости неравенства (4). Отметим, что, внеся в (4), например, x ( t ) = t - a , можно также получить необходимое условие справедливости неравенства (4): b

J ( t - a ) ( 2 p ( t ) + ( t - a ) q ( t ) ) dt <  b - a . a

x (a) = 0, имеет только нулевое решение.

Доказательство. Пусть x - решение

b        (

J ⁽ t ^- a ) p ⁽ t ) + a        \

bb                             i

J q ( s ) ds dt < — , 2

задачи     (7).     Сделав

t

подстановку

t

то неравенство (4) справедливо для x ^{е W} a .

Следствие 1.2. Если

b

x ( t ) = J z ( s ) ds , получим, что z = A K_bz . Если

всех

a неравенство (4) справедливо,

то в силу теоре-

vraisup ( t - a ) p ( t ) + J ( p ( s ) + ( s - a ) q ( s ) ds <  1, t e [ a , b ]

t

то неравенство (4) справедливо для всех ^{x е} W_a .

Следствие 1.3. Если функция b

p ( t ) + J q ( s ) ds не возрастает на промежутке t

b

[ a , b ] и J ( p ( t ) + ( t - a ) q ( t ) ) <  1, то неравенство a

(4) справедливо для всех x е W_a .

Следствие 1.4. Если функция p абсо-b лютно непрерывна, функция p (t) + J q(s) ds не t

мы 1.1 K_b ||< 1 , отсюда)| z || < 2||z ||. Следовательно, если z ^ 0 , то Л > 1 . С другой стороны, если при всех Л е [0,1) задача (7) имеет только нулевое решение, это означает, что все собственные значения (точки спектра) оператора К_ь не превосходят единицы. Из теоремы 1.1 следует справедливость неравенства (4).

В случае, если функция p абсолютно непрерывна на [ a , b ], то задачу (7) можно записать в виде

b

Х( t ) = Л ( p ( b ) x ( b ) + J ( q ( s ) - p ( s )) x ( s ) ds ) , t

убывает на промежутке [ a, b ] и p (b) <—-— , b - a то неравенство (4) справедливо при всех x е Wa.

Из неравенства (6) получаем

Следствие 1.5. Если

x ( a ) = 0.

Следствие 1.6. Если функция p абсолютно непрерывна на [ a , b ] и b

(b - a) p (b) + J (s - a) | p (s) - q (s) | ds < 1, a то неравенство (4) справедливо для всех x e Wa .

Доказательство. Для решения задачи (7) справедлива оценка

b

| x ( t ) | < Л ( ( b - a ) p ( b ) + J ( s - a ) | p ( s ) - q ( s ) | ds ) •

a max | x (t) |.

t е [ a , b ]

Отсюда следует, что при Л е [0,1) эта задача имеет только нулевое решение.

Теорема 1.3 . Пусть функция p абсолютно непрерывна на [ a , b ]. Тогда неравенство (4) справедливо для всех x е W_a тогда и только тогда, когда при всех Л е [0,1) краевая задача

x ( t ) = Л ( ]p ( t ) - q ( t )) x ( t ), x ( a ) = 0,

,x ( b ) = Л р ( b ) x ( b ) имеет только нулевое решение.

Особый интерес представляют случаи, когда обыкновенное линейное однородное дифференциальное уравнение второго порядка (8) можно проинтегрировать. Тогда можно получить точные условия справедливости неравенства (4). Несколько таких случаев рассмотрим ниже.

I. Постоянная функция p ( t ) - q ( t ) = h .

Общее решение задачи (8-9) равно x (t) = <

csh JhA(t - a), c(t - a), h = 0,

c sin л/-hЛ (t - a),  h < 0, где c - произвольная постоянная. Из условия (10) следует, что неравенство (4) справедливо тогда и только тогда, когда bb

Jxc2 (t) dt > y J (2(t - a) | x(t)x(t) | +rx2 (t)) dt aa при всех x е Wa справедливо тогда и только тогда, когда

+-Р cth¹ d , ( b - a )²

Y <         t,

⁷    ( b - a )²

r - 1      2 I --7

------ ctg² T- d , ( b - a )

где d = y (1 - r )( b - a ).

r < 1, r = 1,

1 <  r <  1 +--- ^П-^ ,

4( b - a )² y

Признак 1.2. Неравенство bb

J xc2 (t) dt > y J (2(b -1) | x(t)x(t) | +rx2 (t)) dt aa при всех x е Wa справедливо тогда и только тогда, когда y <—---лг---г 4(b - a)2(1 + r)

• II.    Степенная   функция     р > - 2,

p ( t ) - q ( t ) = h ( t - a ) ^P .

Общее решение задачи (8-9) равно

2 Л h     J+p\

x ( t ) = cP - al j (----- ( t - a ) ² ) при h > 0

P + 2 P ^{+ 2}

(Iv - модифицированная функция Бесселя I рода), и x(t) = c^t - a J j (        (t - a) 2 )

P + 2   P ^{+ 2}

Jh cth Th(b - a), 1 p (b) <[-----, b - a

h = 0,

при h <  0 ( J_v - функция Бесселя I рода).

- -h ctg 4~ h ( b - a ),

-

п² 4( b - a )²

< h <  0.

Для неравенства

(2) (здесь 2 p ( t ) = y ,

q ( t ) = 0, h = 0) это условие принимает вид 2

Y < y =----. Напомним, что ранее точность b - a этой константы установил P.R.Beesack [2]. В случае p (t ) = 0, q(t) = y , h = -y получаем

_     п2

точную константу y = ^^-- у

в неравенстве

Виртингера (1).

Отметим два следствия.

Обозначим через i_v ( m ) наименьший положительный корень функции

I v ^{n ) - (}1 ^{- m )} I v + 2 ^{n )} = 2? I v + 1 ^{n ) + m I} v + 2 ^{n )},

а через J_v ( m ) - наименьший положительный корень функции

^J v ⁽ П ) + ^{(1 - m ) J} v + 2 ⁽ П ) = ^ ^J v + 1 ⁽ П ) ^{+ m J} v + 2 ⁽ П ).

Тогда получим, что неравенство (4) справедливо при всех x е W_a тогда и только

тогда, когда

- J¹^ ⁽ . p ( ^b ) ) <  «TT a S^{2 h} <  р + 2                      ^{( P + 2)}

< i 2 р + 3 ( h ( _b P _a) P +1 ^{p ( b ) ).}

р + 2

Условие (12) является точным. Достаточные условия справедливости неравенства

Признак 1.1. Неравенство

(4) на пространстве W можно получить, например, из неравенства (6):

2     2( b - a ) ^{ц + 1} hp ( b ) ₊(b - a)^ ^    1

ц + 3       ( ц + 2)( ц + 3)  ( b - a )²

Приведем некоторые следствия.

⁽ Ц ^{+ 2)2} i 2 2 ц + 3

ц + 2

Y ц + 1 ^- }

Признак 1.3. Неравенство

J x ² ( t ) dt >  Y J ( t - a ) m ( 2( t - a )| x ( t ) x ( t ) | + rx ² ( t ) ) dt

2(ц +1)(b - a)ц+2, b - a ’

⁽ ц ^{+ 2)2} j 2 2 ц + 3

ц + 2

^ц >- 1,

№ -^{- 1},

a

a

при всех x g W_a справедливо тогда и только тогда, когда

_ j2    (m+n < 4(b - a)m+2    < /2    / m+1 \ j-2m^( d )< (m + 2)2 Yd "i-( d ), m+2                                   m+2

где d - m + 1 - r .

Обозначим через i наименьший положительный корень функции I , а через j – наименьший положительный корень функции J_v .    Отметим, что      i_v - i_v (1) - i_{v 4} (0),

j ; - j ; (1) - j ; - 1 (0).

В случае p ( t ) - 0, q ( t ) - y ( t - a ) ^m и целых m > - 2, рассмотренном ранее в работе [1] (см. также [11, с.437]), получим

Признак 1.4. Неравенство

b

b

-

2( ц + 1)( b - a ) ^{ц + 2},

- 2 <  ц < - 1.

В случае полуцелого индекса, т. е. при 4  8  12

ц - 0,-—,-—, ——,... функции Бесселя можно выразить через элементарные функции. Отсюда, в частности, получаем ряд точных кон-2п2    2.87845768

стант: y  ---1т ~i— ,

¹   ( b - a )²      ( b - a )²

где

„          n ²

cth ^ 1 - П 1 , Y 1 ----------2

- 3    6( b - a ) 3

1.64493407

( b - a ) 3

;

Y з ^-

J &(t ) dt >  y J ( t - a ) m x ²( t ) dt

Y 5 ^- 7

2 n²

15( b - a ) 5

2 ? 25

1.315947254

2 ;

( b - a ) 5

1.15375592

22 ,

35( b - a )⁷     ( b - a )⁷

a

a

где

справедливо тогда и только тогда, когда

П ₅ - наименьшее положительное

- 7

реше-

( m + 2) 2 j² m + 1

_Y <--------- m + 2

4( b - a ) m ^{+ 2}

.

Признак 1.5. Если bh p (t) + [ q (s) ds  ------(t - a)ц+1, t         ц+1

то неравенство (4) справедливо тогда и только тогда, когда

ние уравнения tg n - п , 2п ²₇

- 7      1.05452260

^Y_ 7 ^-            2 ~           2    ’

-⁹   63( b - a )⁹     ( b - a )⁷

где п 7 — наименьшее положительное

- 9

реше-

- j²     <  4( b - a ) ^{ц +} 2 h <  i 2

- ц ³   ( ц + 2) 2      - ц ³.

Рассмотрим теперь более подробно частный случай p ( t) - ^Y ( t - a) ^{ц + 1}, q ( t ) - 0, ко-

торый исследовался ранее в работе [5] лучшая константа y^+i в неравенстве

. Наи-

j x ² ( t ) dt >  y J (t — a ) ^{ц +} 1 1 x ( t ) x ( t ) | dt

b

b

3 n ние уравнения tg п ----- х •

3 - п

Как известно, lim j- - 1 [10, с.192]. От ; ^^ю ;

сюда предельным переходом при ц ^- 2 из полученного выше значения для y^h получа-1

ем y 1 - — .

^{- 1}   2

Если функции Бесселя не являются элементарными, наилучшую константу y^ 1мож-но оценить снизу. Оценивая спектральный радиус оператора K , получаем:

a имеет вид

a

1) Y u + i >

² л/ и ⁺ 2 ( b - a ) ^{U + 2}

(получив в работе[5]

эту оценку, Troy поставил вопрос о точности этой константы. Однако ясно, что, кроме случая и = - 1, она точной не является);

2) Y u + i >

2    <  ( и + 2)( и + 3)(2 и + 5) V⁴

( b - a ) ^{и + 2} 1         и + 7         >

Можно также получить оценку точной константы

Y u + i сверху: Y u + i -

(1 + 2 +U )² 2( b - a ) ^{и + 2}

• III.    Степенная функция со  сдвигом

• p) ( t ) - q ( t ) = h ( t - т ) ^U , т <  a .

Общее решение уравнения (8) равно

U + 2

x ⁽ t ) = tJ -^ T ⁽ C i I ^( U h ⁽ t ^{- т} ) ² ) ⁺

U + 2

U + 2

+ C , K _J U f( t - т )- )),

U + 2

(Kv - модифицированная функция Бесселя II рода), если h > 0, и x(t) = 4Г^ (Ci J^(^u+f

U + 2

( t - T )^T ) +

U + 2

___        U + 2

+ c , Y J^l ( t - т )- )),

U + 2

( Y — функция Бесселя II рода), если h <  0.

Обозначим через k_v (u , ю ) наименьший положительный корень функции

I V + 2 ^(u п ) ^K v ⁽ П ) ^- I v ⁽ П ) ^K v + 2 ^(u П ) ^-

• ^{(i -} ® )⁽ I V + 2 ^(u П ) K v + 2 ⁽ П ) ^- I V + 2 ⁽ n ) K v + 2 ^(u П й и через y „ (u , ю ) - наименьший положительный корень функции

• ^J v + 2 ^(u п ^)Y v ( П ) ^{- J} v ⁽ П ) ^Y v + 2 ^(u п ) ⁺

• ^{(i - ю )(} J v + 2 ^(u П ^)Y v + 2 ⁽ n ) ^- J v + 2 ⁽ n ) Y v + 2 ^(u П ))•

Тогда получаем, что неравенство (4) справедливо тогда и только тогда, когда

• V 2 ff a         U + i   ^V⁴( ^Ь - т ) ^{U + 2 h}-

• -y-2u+3 ((ТГ) 2 , hb :,  P(b)) -   (U + 2)2   -

  /      ^U+2                 \

• - k_ ⁽ ( e ) ■ . h^ p ( b ) )

U + 2

Отметим некоторые частные случаи, соответствующие полуцелому индексу функций Бесселя.

Если и = - 4, то k ₅ (u , ю ) является наи

- 2

меньшим положительным корнем уравнения

П      п ² ю + 3            .

cth(u - 1) п =-- , а y ₅ (u , ю ) - уравне-

3 п        - 2

ния ctg(u - 1) п = ^^ ³.

3 п

Если и = 0, то k ₃ (u , ю ) является наи

• - 2

меньшим положительным корнем уравнения cth(u - i) n = -пю , а y ₃ (u , ю ) - уравнения

• - 2

ctg(u - i) n = пю .

• 4          ,,

Если и = —, то k j (u , ю) является 3

наименьшим положительным корнем уравне-

И ю -1 -u п2ю       „, ния cth(u - 1)п = —-----;------, а y i (u ,ю) - n(й ю -u - ю)-2

уравнения ctg(u - 1) п =

• 1    - ю - u п²ю п (й + ю - u ю )

Если и = —, то kj (u , ю) является наи-5

меньшим положительным корнем уравнения cth(u - 1) п =

3(1 - ю )(3 - 3u п ² + u ² п ²) - п ²(3 + u ² п ²)ю

3п((1 - ю)(3й -u 2п2 - 3) -u п2ю), а yj (u ,ю) - уравнения ctg(u - 1)п =

= 3(1 - ю )(3 - u ² п ² + 3u п ²) + п ²(3 - u ² п ²) ю . 3 п ((1 - ю )(3й + u ² п ² - 3) + u п²ю )

Введем обозначения:  kv (u ) = kv (u ,1), yv(u ) = yv(u ,1).

Признак 1.6. Если b_h

P(t) + J q(s) ds = —(t- т)U , то неравенство (4) справедливо тогда и только тогда, когда

^- y ² 2 и + 3

U + 2

^(ь ■h - ( и + 2) 2

,        ^{U +2} \

^{- k 2} 2 и + 3 ⁽ (H) ² ).

U + 2

Выпишем также некоторые достаточные условия справедливости неравенства (4). Из следствия 1.5 получим p (b)--- ((b - т)"+1 - (a - т)"+1) < —.

* +1                     b - a

Из следствия 1.2 получаем h < 0, p (b) - -h- (b - т)"+1 +

* +1

h       ( b - т ) * ^{+ 2} - ( a - т ) * ^{+ 2}     1

( * + 1)( * + 2)         b - a          b - a

• IV. Степенная функция со сдвигом p ( t ) - q ( t ) = h ( т - 1 ) * , b <  т .

Общее решение уравнения (8) * + 2

x ⁽ t ) = 4 -4 ⁽ cI ^(^^ ^{( т -} t ) ² ) ⁺

* + 2

• *+2

+ c , K _А( « ( т - t )- )),

* + 2

если h > 0, и  *

x(t) = ^/г-7(cJ_l(2*+F (т - t)2

* +2

* + 2

+ c 2 Y Л^ т - t *)), * + 2 если h < 0.

Отсюда получаем, что неравенство (4) справедливо тогда и только тогда, когда - У : * > ( (Э) ⁺ • - 7 7 * 7+1 p ( ^b ) ) <  ⁴ 7 /2 ^h <

/       * ⁺²                   \

• < ^ =* . , ⁽ ( а ) 2 . - т т т -^+т p ( ь ) ) •

* + 2

	s p ( s ) + J q ( т ) d т
Ka ( t , s ) = •	a t p ( t ) + J q ( т ) d т a

a <  s <  t <  b , a <  t <  s <  b .

Теорема 2.1. Неравенство (4) справедливо для всех x e W^b тогда и только тогда, когда || к “ ||< 1.

Теорема 2.2. Неравенство (4) справедливо для всех x e W^b тогда и только тогда, когда при всех Л e [0,1) задача t

x(t) = Л(J(p(s)x(s) - q(s)x(s))ds - p(t)x(t)), a x (b) = 0 имеет только нулевое решение.

Теорема 2.3. Пусть функция p абсолютно непрерывна на [ a , b ]. Тогда неравенство (4) справедливо для всех x e W^b тогда и только тогда, когда при всех Л e [0,1) краевая задача

x ( t ) + Л ( p ( t ) + q ( t )) x ( t ) = 0, x ( b ) = 0,

x ( a ) + Л p ( a ) x ( a ) = 0 имеет только нулевое решение.

• I.    Постоянная функция p ( t ) + q(t ) = h .

2. Неравенство с условием x ( b ) = 0

Неравенство (4) на пространстве W b справедливо тогда и только тогда, когда

Интегро-дифференциальное неравенство (4) с условием x ( b ) = 0 рассматривается полностью аналогично.

Обозначим через W^b пространство таких абсолютно непрерывных функций x :[ a , b ] * R , что .x e L₂ и x ( b ) = 0.

Пусть функции   p,   q:[ a, b] * R измеримы и неотрицательны на [ a, b ], причем bt j (b -1)(p (t) + J q (s) ds )2 dt < да. aa

Ядро      интегрального      вполне непрерывного    оператора    Ka : L2 * L2

определим равенством

Th ctg Jh ( b - a ),

p(a) Я     -—, b -a_____ 4~h cth ^-h(b - a),

< — ^П-- 4( b - a )²

h = 0,

h <0.

II.  Степенная функция

* >  - 2,

p ( t ) + q ( t ) = h ( b - 1 ) * .

Неравенство (4) на пространстве W ^b справедливо тогда и только тогда, когда

i2„    (*+

- ² * ^{+ 3}     h ( b - a ) * ^{+ 1}

* + 2

p(a )) < 4

(b - a ) *+2 (* + 2)2

h <

',   ,( * +1—

- ² * ^{+ 3}     h ( b - a ) * ^{+ 1}

* + 2

p(a)).

III. Степенная функция со сдвигом p ( t ) + q ( t ) = h ( т - 1 ) ^А , b <  т .

Неравенство (4) на пространстве W ^b

справедливо тогда и только тогда, когда

А + 2                    (⁺-лУ ^{+ 2}

- k\^з( ) 2 ,-- p ( a)) <  4 ^Т a ) ₇ h <  - 2 ³ vV r ^- а/    , h ( т - a ) А + 1      "      ( а + 2)²

А+ 2

< У 22 А+з(( %)“, -       p (а)).

——— ⁴    '        h (т - а ) ^А

А + 2

IV. Степенная функция со сдвигом p ( t ) + q ( t ) = h ( t - т ) ^А , т <  a .

Неравенство (4) на пространстве W ^b справедливо тогда и только тогда, когда

,     ,   , А + 2      .               (⁺-rV ^{+ 2}

- k \_u+?((— ) 2 ,   ^{А +}\, p ( a )) < 4 ⁽ a ^T ) , h <

- г^ vy a ^- t)    , h ₍ a - T ) ^{А +1}^V V     ( А + 2)²

А + 2

У ²2 А + з ( ( т )“, - ^А + т p ( а )).

h ( a -т ) ^А

А + 2

Отметим, что Q = maxmin(||K 11,1 KclI) = c e[ a, b ] 11 II II mi"maxK UKclb'

Теорема 3.1. Неравенство (4) справедливо для всех x e W b тогда и только тогда, когда Q <  1.

Доказательство. Пусть неравенство (4) справедливо для любой функции x e W^b . Покажем, что тогда

J x ²( t ) dt >  J ( 2 p ( t )| x ( t ) x ( t ) | + q ( t ) x ²( t ) ) dt

* c

* c

a

a

для любой функции x e W_a или же

J x ² ( t ) dt >  J ( 2 p ( t )| x ( t ) x ( t ) | + q ( t ) x ²( t ) ) dt

b

b

* c

* c

для любой функции x e W^b . Предположим, найдутся две такие функции x_a e W_a и x_b e W^b , что

3. Неравенство с условиями

x (0) = x (b) = 0

J x ²⁽ t ) ^dt <  J ^{( 2} p ⁽ t ^)| x a ⁽ t ) ^x a ⁽ t ) ^{1 +} q ⁽ t ) x ²⁽ t ) ) dt ^,(14)

* c

* c

Обозначим через W b пространство таких абсолютно непрерывных     функ ций x:[ a, b ] ^ □ , что x e L2 и x (a ) = x (b ) = 0.

Пусть функции  p, q:[ a, b ] ^ □ измери мы и неотрицательны на [ a, b ], причем

J ( t - a ) ( p ( t ) + J q ( s ) ds ) ² dt + at bt

J ( b - 1 ) ( p ( t ) + J q ( s ) ds ) ² dt < » cc при каждом c e [ a , b ].

Рассмотрим неравенство (4) в пространстве W_b . Разобьем промежуток [ a , b ] на отрезки [ a , c ] и [ c , b ] и сведем таким образом неравенство (4) к задаче (5) на промежутке [ a , c ] и к аналогичной задаче на промежутке [ c , b ] .

Так как величина Ц к Ц не убывает и непрерывна по c , || ^^c || не возрастает и непрерывна по c , причем || K _a || = || K b ||=0, то существует такая точка c ' e ( a , b ), что Q% c -11=1 K 'I I-

a

b

a

b

J ^x 2 ⁽ t ) dt <  J ⁽ 2 p ⁽ t ^{)| x} b ⁽ t ) x b ⁽ t )^{| +} q ⁽ t ) ^{x 2(} t ) ) ^dt .⁽¹⁵⁾

c

c

Если x_a ( c ) = 0 и x_b ( c ) = 0, то для функции

^{x (} t ) = *

ство

x„ ( t )

——, t e [ a , c ], x a ( c )

справедливо неравен-

^7), t e [ c , b ],

I ^x b ^{( c} )

bb

Jx2(t)dt < J(2p(t)| x(t)x(t) | + q(t)x2(t))dt, aa что приводит к противоречию. Если же xa (c) = 0 , то это неравенство справедливо для

М  f xa (t)’    t e[a, c], Ы функции x(t) = *                 И наконец,

[ 0,          t e [ c , b ].

если xb (c) = 0, то оно справедливо для функ-f0,         t e[a,c], ции x(t) = *                  Итак, выполня-

[ x b ( t ),      t e [ c , b ].

ется хотя бы одно из неравенств (14), (15). Тогда в силу теорем 1.1 и 2.1 Q =1 \^K. -1=1 K ^-||< 1'

Пусть теперь Q <  1. Тогда для любого x e W^b в силу теорем 1.1 и 2.1 справедливы неравенства (14) и (15). Складывая эти неравенства, получаем (4).

Следствие 3.1. Если cc maxmin(J (t - a)(p(t) + J q(s)ds)2 dt, ce[ ab1            a                             t bt

J(b - t)(p(t)+J q(s) ds )2 dt) < -, cc то неравенство (4) справедливо для всех x e Wb.

Следствие 3.2. Если max min c e[ a, b ]

c

( vraisup(( t - a ) p ( t ) + J ( p ( s ) + ( s - a ) q ( s )) ds ), ‘ e[ a , c ¹                                                 t

t vraisup((b -1)p(t) + J (p(s) + (b - s)q(s)) ds)) < 1, te[c,b 1                                                c то неравенство (4) справедливо для всех

X e W .

Следствие 3.6. Если функция p абсолютно непрерывна и c max min((c - a)p(c) + [ (s - a) | p (s) - q(s) |ds, ce[a,b1                                      J

a

(b - c) p (c) + J (b - s )| p (s ) + q (s ) | ds ) < 1, c то неравенство (4) справедливо для всех x e W.

Отметим, что, положив, например, в (4)

^{x (} t ) = *

Следствие 3.3. Если

c max min(vraisup(c - a)(p(t) + J

c e[ a , b 1                    t e [ a , c 1

t

t vraisup( b - c)(p (t) + J q (s ) ds )) < 1, t e[ c, b 1                               c

то неравенство x e W .

(4) справедливо для всех

Полагая в

следствии 3.3 c = — ( a + b ), 2

получаем

t - a ,

b - 1 ,

. г a + b t el a ,-------

,2

a + b

],

, можно получить

, b ],

также необходимое условие справедливости неравенства (4):

a + b

J ( t - a ) ( 2 p ( t ) + ( t - a ) q ( t ) ) dt + a

b

+ J ( b - 1 ) ( 2 p ( t ) + ( b - 1 ) q ( t ) ) dt <  b - a .

a + b

Рассмотрим теперь некоторые простые частные случаи.

I. p ( t ) = y , q ( t ) = 0.

Из формул (11) и (13) получаем

Y < y =----. Напомним, что константа y b - a была ранее получена Olech [3], Opial [4].

Следствие

3.4. Если a+b

max(vraisup(p (t) + [ q(s)ds), г +b,                  .

t e[ a,—1                  t vraisup(p(t) + J q(s)ds)) < ——, t e[ a ', b 1            a+b                 b - a то неравенство (4) справедливо для x e W.

всех

Из 3.4 получаем

Следствие 3.5. Если a+b

2b vraisup p (t) + max( J q (s) ds), J q (s) ds) <-----, te[ a.b 1                     Ja              a + b               b - a то неравенство (4) справедливо для всех X e W.

• II.    p ( t ) = 0, q ( t ) = y .

Из формул (11) и (13) получаем, что n

Y <  y =------ y . Эта константа получена ра-

( b - а )²

нее с помощью методов классического вариационного исчисления.

• III.    p ( t ) = y ( t - a ) , q ( t ) = 0 (или

p ( t ) = Y ( b - 1 ), q ( t ) = 0).

Из формулы (11) получаем, что 2

i ₃

Y <---2-y (здесь корень функции Бесселя

( c - а )

i , ~ 1.199678640является решением уравне- ^- 2

ния п = cthn). Из формулы (13), что arcctg2 (i )

Y < ——---рт²— . Таким образом,

У <  г =

( i з + arcctg( i 3 )) 2

__22__

( b - a )²

3.589314557

( b — a )²

если чаи.

m <  0 . Отметим некоторые частные слу-

IV. p ( t ) = y ( t - a ), q ( t ) = y r, 0 <  r <  1,

При m = -

(или p ( t ) = y (b - 1), q ( t ) = y r , 0 <  r < 1).

Пусть 0 - наименьший положительный корень уравнения 0 = V r - 1 ctg 4r - 1 0  при

вид

— з2

точная константа имеет

1.457960692

^Y           2 ~           2

3( b - a )³      ( b - a )³

,

r >1, 0 = 1 и 0 - положительный корень уравнения    0 = 71 - r cth 71 - r 0    при

0 < r < 1. Из формулы (11) следует,  что у <---r—7. Из формулы (13) получаем, что

( c - a )

где 3 = cth( 3 - ^П ) » 2.09138281.

При m = - — точная константа имеет вид

з2

1.015760115

2z 0

arcctg² ( ^r )

у <-------- ^1^{+ r} .

(1 + r )( b - c )²

Отсюда

I 71 + r0r + arcctg(

V                 V1 + r J

Y < Y =

(1 + r )( b - a )²

Отметим, что при r = 1

G/2 + arcctg )

2     2.807336637

У <  У =----------^---~--------;--

2( b - a )²          ( b - a )²

^Y             2 ~            2     ,

15( b - a )⁵     ( b - a )³

где 3 3 cth( 3 - п ) = 3 ² + 3, 3 « 3.90338337 .

Y

В сингулярном случае q (t) =----(или t - a

Y q (t) =----) имеем b -1

b

a

b ₁

\1 X ( t ) x ( t ) | dt a t ^- a

bb

(f x ² ( t ) dt >  y[ -----1 x ( t ) x ( t ) | dt )

^{J             J} b - 1

a

a

V. p ( t ) = y ( t - a ) m , m >- 1, q ( t ) = 0 (или

при всех x g W« ,

11 если y < —. Константа — 22

p ( t ) = y ( b - 1 ) ^m , m >- 1, q ( t ) = 0).

Из формулы (12) следует, что

■ 2      _< , Ym ⁽ c ^- a ) m +¹ z -2

^J - 2 m + 1 “      ( m + 1)²    “- ²

m +1            \        '              t

Аналогично имеем

Y m ( c - a ) ^{m + 1} ( m + 1)²

( m +1 A b - a

⁽ c - a ) I - ⁴

y 2 m + 1

m + 1

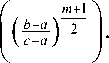
Обозначим через y - ¹ и k ^- функции, обратные к функциям y , k соответственно. Тогда

⁽ m ^{+ 1)2} i 2 m + 1⁽ У '2 m + 1 ⁽ i 2 m + 1 ^{) ) 2}

у у  ____________ m +1 ______ m +1 ____ m +1 _____

• ^Y~^Y~         4 m ( b - a ) ^{m + 1         ,}

если m >  0 , и

( m + 1) 2 j 2m, ( k ^- 2 . „ ( j 2 . + 1 ) ) 2

—___ m + 1 ______ m + 1 _____ m + 1 _____

• ^У~^У~           4 m ( b - a ) ^{m + 1}         ’

здесь точная.