Обобщенное представление динамического гашения колебаний как дополнительной обратной связи

Динамическое гашение колебаний является достаточно известным и распространенным способом изменения динамических свойств систем в задачах защиты от вибраций машин, приборов и оборудования. Многие вопросы, значимые для практики, представлены в работах [1 ^ 4 ]. Вместе с тем в методических подходах, связанных с выбором параметров динамических гасителей, возникает ряд проблем, которые требуют внимания и учета особенностей построения виброзащитной системы (ВЗС) с точки зрения учета ее структуры, числа степеней свободы, соотношения форм движения по отдельным степеням свободы. В таких случаях свойства динамического гашения колебаний проявляются опосредованно, через возникающие дополнительные связи, изменяющие предварительно выбранные значения параметров, рекомендуемых в упомянутых выше работах.

I. Постановка задачи

Постановка задачи исследования основана на представлении о возможности построения динамического гасителя колебаний в ВЗС как введения в механическую колебательную систему любой сложности дополнительной обратной связи [4]. Такие приемы основаны на использовании методов структурной теории виброзащитных систем (ВЗС) и позволяют достаточно просто создавать алгоритмическую базу для расчетов режимов динамического гашения. Используя идеи, изложенные в работе [1], рассмотрим систему с двумя степенями свободы (силы сопротивления полагаются на предварительном этапе малыми) цепного типа, для которой на рисунке 1 а приведена расчетная, а на рисунке 1 б - структурная схемы эквивалентной в динамическом отношении системы автоматического управления [4].

:^k ,

Q

z 1

k

k

У ,

k

m ,

: k ,

У 2

mp

m 2 P

m

' ^k 1

z

■ 1

Q

У 1

-1

а

б

Рис. 1. Расчетная (а) и структурная (б) схемы виброзащитной системы с динамическим гасителем

На рисунке 1 объект защиты имеет массу m 1 , а динамический гаситель - соответственно m 2. В системе рассматривается силовое - гармоническая сила приложена к объекту защиты, а также кинематическое возмущение z 1 , определяемое гармоническим движением основания. Система координат у 1 и у₂ связана с неподвижной системой отсчета. Приведенные на рисунке 1 а, б схемы носят обобщенный характер, что позволяет по отдельности исследовать типовые ситуации.

II. Некоторые типовые случаи динамического гашения колебаний

Простейший пример динамического гашения колебаний представлен в работе [1] и соответствует набору параметров: P * 0 , z i = 0, k i = 0, к 2 * 0 , что принято на расчетной и структурной схемах виброзащитной системы, как показано на рисунке 1 а, б. В данном случае объект защиты массой m 1 может совершать независимое движение, т.е. имеется циклическая координата, определяющая некоторое установившееся движение. Динамический гаситель массой m 2 обеспечивает колебательные движения относительно установившегося движения; к объекту защиты массой m 1 приложена гармоническая сила Q = Q 0 sin rot . Делая ряд структурных преобразований, можно получить структурную схему виброзащитной системы (ВЗС), отражающей специфику рассматриваемого примера (рис. 2).

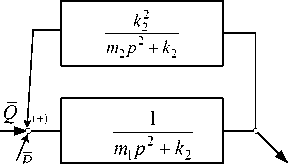
Рис. 2. Структурная схема ВЗС при установившемся движении объекта защиты

У 1

Передаточная функция ВЗС (см. рис. 2) в этом случае принимает вид

W_v = I¹ =

1 Q

2 . , m 2 Р + к 2

⁽ m 1 р ² + к 2 ⁾⁽ m 2 р ² + к 2 ) ^- к 2

или

W = y- = , ¹ p   p ² [

m 1 Р ² + к 2 _______ 2

m 1 m 2 p + к 2 ( m 1 + m 2

Из (2) определяется (член знаменателя перед скобкой - р² ), что ВЗС участвует в двух движениях: одно характеризуется циклической координатой (некоторое установившееся движение); второе инициируется гармонической силой P , при этом соответствующая передаточная функция записывается так:

W2 = 21 =     m 2 Р 2 + k2

^p m 1 m 2 p ² + к 2 ( m 1 + m 2 )

.

Используя (3), найдем, что ВЗС будет иметь частоту собственных колебаний 2 ₌ k 1⁽ m + m 2 ) ^го соб                 ’

m 1 m 2

а также частоту динамического гашения

„ 2   = k 2

® дин

.

m 2

Амплитудно-частотная характеристика ВЗС, соответствующая выражению (3), приведена на рисунке 3.

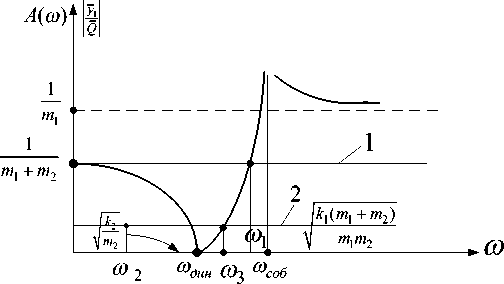
Рис. 3. Амплитудно-частотная характеристика ВЗС при установке динамического гасителя на объекте, совершающем некоторое независимое движение

Отметим, что в рассматриваемом примере режим динамического гашения предшествует резонансу; в зарезонансной области амплитуда колебаний y i стремится к установившемуся значению —, т.е. зависит от массы объекта защиты. m i

• III.    Динамическое гашение как задача управления

Физический смысл передаточной функции (3) заключается в определении динамической податливости объекта при действии силы Q [1]. Выражение для амплитудно-частотной характеристики (АЧХ) можно получить, используя (3):

( к2 — m2® 2 )

A ( ® ) = ------¹ ------2 .                                    ⁽⁶⁾

^ [ ( m i + m 2 ) k 2 - m i m 2 ® ² ]

На рисунке 3 отмечен ряд характерных особенностей АЧХ: при ® ^ 0 : A (0) ^------- ;

m i + m 2

при ® ^да- A (®) ^ —; в дорезонансной области имеется зона с ниспадающими ветвями АЧХ, mi что представляет интерес для реализации режимов динамического гашения. Если провести на рисунке 3 параллельную линию 1, что соответствует ординате 1   , то из выражения (6) можно mi + m 2

получить значение частоты

2 2 k ₂ ( m + m ₂) ® = —-—¹--—,

m i (2 m i + m 2 )

.

которое определяет частотный интервал 0 — ® , при нем податливость ВЗС будет равна------- m i + m 2

Если ввести параметр a, определяющий значение податливости меньшее, чем -------, что соот- mi + m 2

ветствует на рисунке 6 линии 2, то можно получить значения частот ® 2 и ® 3 , определяющих соответствующий интервал частот эффективной работы гасителя. В этом случае необходимо решить алгебраическое уравнение

2х2Г 2     2, х21

( ® ) I m 2 — a ( m i m 2 ) 1 +

+ ® 1 2 a k 2 m i m 2 ( m i + m 2 ) — 2 k 2 m 2 1 +

, 2      2 z             x 2,2

+k2 — a (mi + m2) k2 = 0, полученное из (3) при a <

m i + m 2

Выражения (7), (8) могут быть использованы для выбора рациональных параметров ВЗС, исходя из соображений, что m 2 » 0,15 ^ 0,20 m i [1].

• IV.    Особенности в задаче управления колебаниями

Введение динамического гасителя в виде присоединения к объекту дополнительной массы m 2 и упругого элемента с жесткостью k 2 приводит к изменению структуры и динамических свойств исходного объекта, что можно обобщить следующим образом.

• 1.    Если до введения дополнительной связи объект защиты, находящийся под действием силы P _, имел передаточную функцию

• 2.    При таком представлении ВЗС введенный динамический гаситель реализуется в виде дополнительной положительной обратной связи с передаточной функцией колебательного звена

• 3.    Второй типовой случай соответствует классической схеме динамического гашения колебаний при силовом, а также при кинематическом возмущениях, основными своими фрагментами представлен в работе [5]. В нашем случае такому примеру соответствуют расчетная и структурная схемы на рисунке 1 а , б при следующих параметрах: к 3 = 0, k i * 0, к 2 * 0 , z i * 0 , P * 0 . Преобразованной соответствующим образом расчетной схеме соответствует структурная схема на рисунке 4.

  

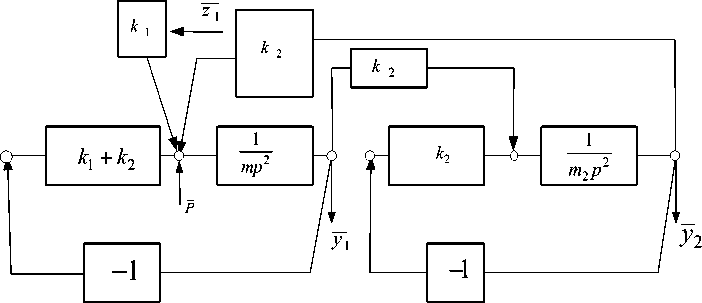
  Рис.4. Структурная схема динамического гасителя колебаний: m 1 – масса объекта защиты; m 2 – масса динамического гасителя

  
  

W = И = -Ц,                                (9)

P m1 p где p = jm — переменная Лапласа, то после введения дополнительной связи передаточная функция

ВЗС, включающей в свой состав объект защиты, будет определяться из структурной схемы эквивалентной в динамическом отношении (САУ), приведенной на рисунке 3. При этом упругий элемент k 2 входит в структуру парциальной системы ВЗС, содержащей объект защиты, а передаточная функция парциальной системы принимает вид

W ' =

m i p + к 2

k 2²

.

доп m 2 P + к2

Режим динамического гашения в системе по координате y ₁ обеспечивается на частоте, определяемой выражением (5). На этой частоте дополнительная обратная связь приобретает бесконечно большое значение коэффициента усиления звена.

Как следует из рисунка 4, виброзащитная система состоит из двух парциальных систем. В первую входит объект защиты массой m1 и два упругих элемента с жесткостями k1 и k2 . Вторая состоит из элемента массой m2 и упругого элемента k2. Приведенная схема ВЗС показана на рисунке 5, где введенный динамический гаситель представлен в первой парциальной системе как дополнительная обратная связь с передаточной функцией колебательного звена из элементов k2 и m2 .

Передаточная функция ВЗС при силовом возмущении имеет вид

W1 = 21 =__________m 2 P 2 + k 2___________;

p ⁽ m l p ² + k i + k 2 ⁾⁽ m 2 p ^{2 + k} 2 ) - ^k 2

при кинематическом возмущении -

W2 = 21 =_________k1( m2 p 2 + k2)_________.

z l ⁽ m i p ² + k i + k 2 ⁾⁽ m 2 p ^{2 + k} 2 ) - ^{k 2}

Из выражений для передаточных функций (12), (13) можно найти частоту динамического гашения:

®Дин = — ’ m 2

что совпадает с выражением (5) для первого типового примера. Частоты собственных колебаний ВЗС определяются из частотного характеристического уравнения:

m1 m 2 p 4 + p 2(k1 m 2 + k2 m 2 + k1 m1) + k k2 = 0.

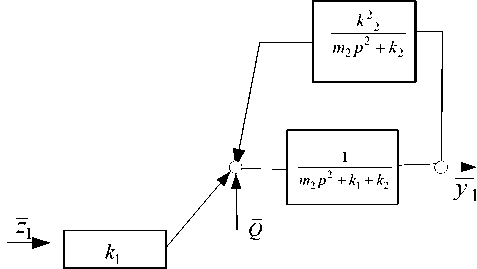
Рис. 5. Детализированная структурная приведенная схема динамического гасителя

Амплитудно-частотная характеристика ВЗС приведена на рисунке 6.

Кривая 1 ( А 1 ( щ ) ) отражает изменения динамической податливости при действии внешней силы P , тогда как A ₂( ю ) показывает, как изменяется величина коэффициента передачи амплитуды колебаний Z 1 на объект защиты m . Частоты собственных колебаний в обоих случаях возмущения совпадают, так же как и частоты динамического гашения. Области эффективной работы динамического гасителя колебаний могут быть найдены аналогичным, что и для первого случая, приемом, это позволяет определить соответствующие границы частотных интервалов ^ ^ — б/ъ .

Таким образом, введение динамического гасителя как обратной дополнительной связи принимает соответствующую форму на структурной схеме (рис. 8 б) цепи с передаточной функцией

W =____'____ ,                                                     (16)

m 2 p ² + k 2

что совпадает со схемой на рисунке 2. Вместе с тем характер связей внутри ВЗС меняется. Так, в парциальной системе, включающей объект защиты, появляются упругие элементы с жесткостями k 1 и k 2 . При этом передаточная функция парциальной системы принимает вид

W =     ₂ ¹ ------,                                             (17)

m 1 p ² + k 1 + k 2

что отражает при формировании структуры парциальных систем, связанных с объектом защиты, некоторые общие свойства. Последнее заключается в том, что объект защиты в свой состав включает не только упругий элемент гасителя - k ₂ , но и упругую связь объекта защиты с конструктивной основой ВЗС через элемент с жесткостью k ₁ .

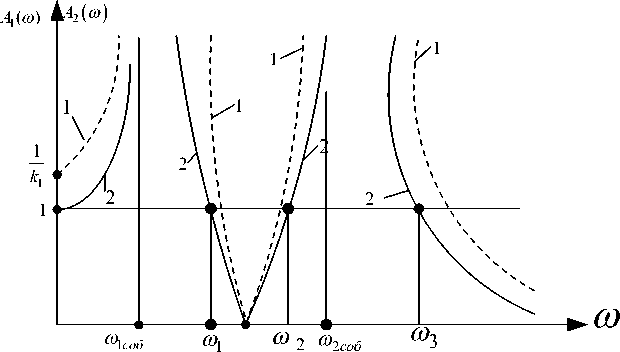
Рис. 6. Амплитудно-частотные характеристики ВЗС для подпружиненного объекта защиты:

A i ( to ) — кривая 1 соответствует (12); A 2 ( to ) — кривая 2 соответствует (13)

• V.    Возможности развития подхода

Усложнение связей объекта защиты массой m1 с конструктивной основой ВЗС можно отра- зить на примере системы с тремя степенями свободы, как это показано на рисунке 7а. Структурная схема виброзащитной системы, соответствующей расчетной схеме на рисунке 7, имеет вид, как

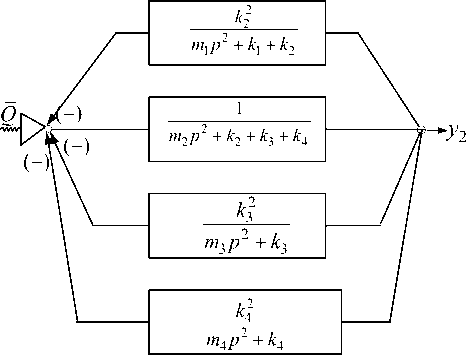
б

Рис. 7. Расчетная (а) и структурная (б) схемы для системы с тремя степенями свободы

показано на рисунке 7 б .

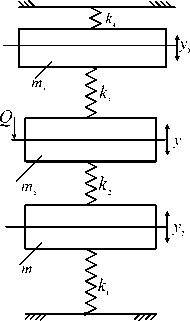
а

Передаточная функция ВЗС при внешнем воздействии Р , как следует из рисунка 7, имеет вид

W = yl =

P

2   22

( m i p + k i + k 2 )( m 3 p + k з )( m 4 p + k 4 )

( m i p 2 + k i + k 2 )( m 2 p 2 + k 2 + c + k 3 + k 4 ) — k 2

.        2 ' ( m 3 p +

—

+ k 3 ) — ( m i p ² + k i + k 2 ) k 3;( m 4 p ² + k 4 )

— ( m 3 p + k 3 )( m i p + k i + k 2 ) k 4 .

Знаменатель (18) представляет собой характеристическое уравнение, из которого могут быть определены частоты собственных колебаний.

Что касается режимов динамического гашения, то в данном случае из (18) следует, что их может быть три, что определяется следующими выражениями:

2       к д •    2        ^к 3 •    2       к + ^k 2

®\ дин =    ; ® 2 дин =     ; ® 2дин =      ^2.                                     (1 ⁹⁾

m ₄           m ₃             m ₁

Реализуемость совместных режимов динамического гашения, например ю 1 _дин = ю _2дин или ^Ю 1 дин = ^ю 2дин = ^ю 3дин , требует отдельного рассмотрения с привлечением информации о значениях частот собственных колебаний, которые также могут совпадать с частотами динамического гашения колебаний.

• VI.    Заключение

Присоединение динамического гасителя к объекту защиты в виде свободного тела или элемента некоторой конструкционной основы в рамках структурной теории виброзащитных систем [4] может рассматриваться как введение в структуру ВЗС дополнительных положительных обратных связей. Передаточные функции таких связей формируются колебательными структурами, характер которых определяется особенностями парциальных систем, включающих объект защиты. Формирование дополнительной связи требует учета конструктивных особенностей объекта защиты и учета возможностей появления дополнительных режимов динамического гашения. Структурные схемы ВЗС и технология их построения предполагают возможности введения параллельно упругим элементам, связанным с объектом, элементарных звеньев других типов.