Обобщенный закон Хаббла в реляционном подходе

В настоящее время теоретическая физика исследует мир в рамках трех парадигм: теоретикополевой, геометрической и реляционной. Первая в настоящее время является доминирующей, объектом исследования ее теорий являются поля (как материи, так и переносчиков взаимодействий) на фоне априорно заданного классического пространства-времени. В основе геометрической парадигмы лежат представления об искривленном пространстве-времени и производных из него физических объектах, в ее рамках работает общая теория относительности (ОТО) и смежные с ней теории. Реляционная парадигма сегодня менее известна, однако ее истоки лежат в работах Г. Лейбница, Э. Маха и других мыслителей, а созданием теорий на ее базе занимались Р. Фейнман, Я. И. Френкель, А. Фоккер, Ф. Хойл, Д. Нарликар и ряд других физиков-теоретиков (см. напр. [1, 2] ).

В основу реляционной теории кладутся три взаимосвязанных аспекта [3, с. 16]: 1) реляционный под-ходк природе пространства-времени (вторичность по отношению к более фундаментальным закономерностям микромира), 2) описание взаимодействий в рамках концепции дальнодействия, 3) обусловленность локальных свойств материи глобальными свойствами всего окружающего мира (принцип Маха). Авторы, следующие реляционному подходу в ХХ веке, принимали во внимание не все указанные аспекты, в частности, игнорировали первый. По этой причине их теории носили эклектичный характер и оказывались недостаточно обоснованными.

Общепринятая космологическая модель ΛCDM, претендующая на полное описание Вселенной как целого, основана на фридмановских решениях уравнений Эйнштейна, то есть строится в рамках геометрической парадигмы. В ней возникает ряд проблем, связанных с необходимостью введения в теорию ненаблюдаемых видов материи, таких как темное вещество и темная энергия. На настоящий момент нет прямых свидетельств реального существования этих субстанций, а само их наличие в теории ставит меж-парадигмальные вопросы об их физической природе и микроскопической структуре, решение которых в рамках теории поля пока не находит существенного успеха. Напомним, что в случае с темной энергией также остается нерешенной проблема сильного несовпадения плотности энергии вакуума в теории поля, с которой связывается космологическая постоянная, и соответствующей величины плотности темной энергии, оцениваемой в геометрической парадигме.

Когда появляются подобные вопросы, затрагивающие основы мироздания, необходимо обращаться к самым фундаментальным представлениям и смотреть на возникшие проблемы с разных сторон, соот- ветствующих разным физическим парадигмам. Исходя из этого, в данной работе исследуется реляционное описание космологических эффектов и на этой основе предлагается обойти типичные для двух других парадигм проблемы космологических моделей.

В задачи реляционной космологии прежде всего входит описание известных модельно независимых наблюдений. Основным таким наблюдением является космологическое красное смещение, проявляющееся в сдвиге спектров далеких астрономических объектов в длинноволновую область. Экспериментально установлен следующий закон для величины красного смещения [4, с. 55]:

"0Г1 /     a н 2 г²

г

* + 2 依 ^{+ 2)}-＞ ，

где Но — постоянная Хаббла, значение которой на сегодняшний день составляет [5] Но = 73.24 士 км/с

^{1 . 74} Мпк^,

а до — так называемый параметр замедления, который в ACDM модели связывают с про явлением ускоренного расширения Вселенной, его современная оценка [6] до = —0.53+°'17. В рамках реляционного подхода предлагается последовательное обоснование этого закона и предпринята попыт- ка оценить названные космологические параметры.

2.    Принципы бинарной предгеометрии

Поскольку реляционный подход к мирозданию пока недостаточно широко известен, кратко изложим его основные положения и главные следствия.

• 1.    В реляционном подходе пространство-время рассматривается как абстракция от системы отношений (расстояний, интервалов) между событиями (объектами). Согласно этой точке зрения, должны рассматриваться лишь переходы между некими начальными и последующими состояниями систем. Это означает задание двух множеств состояний (элементов) и числовых (вещественных или комплексных) отношений между ними. В классической теории это интервалы, а в квантовой теории – амплитуды вероятностей переходов.

• 2.    Между всеми парами элементов двух множеств устанавливаются отношения, образующие мировую матрицу.

• 3.    Постулируется, что вводимые отношения не произвольны, а удовлетворяют некому алгебраическому закону ①①連),связывающему отношения между г элементами первого множества и s элементами второго множества.

• 4.    Самым существенным образом используется свойство фундаментальной симметрии, означающее, что закон удовлетворяется для любых г и s элементов из данных множеств.

• 5.    В работах группы Ю. И. Кулакова [7, 8] были найдены все возможные законы для вещественных отношений, а в работах [9, 10] они были обобщены на случай комплексных отношений — была развита теория бинарных систем комплексных отношений (БСКО), названная бинарной предгеометрией.

• 6.    Было показано, что от теории бинарных систем отношений путем своеобразной “склейки” элементов двух множеств можно перейти к теории систем отношений на одном множестве элементов, которые оказались соответствующими известным видам геометрий с симметриями.

• 7.    В рамках данного подхода было показано, что элементы теории БСКО ранга (3,3) описываются 2-компонентными спинорами, что после своеобразной “склейки” элементов приводит к унарным геометриям в 4-мерном пространстве-времени с сигнатурой (+----). Таким образом, на основе БСКО ранга

• 8.    Бинарная предгеометрия обосновывает два вида представлений: координатное (пространственно-временное) и импульсное (пространство скоростей). Дело в том, что элементы каждого множества в бинарной предгеометрии характеризуются параметрами, определяемыми через отношения к эталонным элементам другого множества. Но поскольку каждое множество является предыдущим к последующему и одновременно последующим к некому предыдущему, то каждый элемент характеризуется двумя наборами параметров. Параметры, определяемые из отношений к эталонным элементам в про-

• шлом, естественно считать прообразами координат пространства-времени, а параметры, определяемые отношениями к эталонным элементам будущего, — считать прообразами компонент скоростей или импульсов. Такое свойство называется двойственностью БСКО.

• 9.    В рамках бинарной предгеометрии на основе БСКО более высоких рангов (4,4) и (6,6) строится теория, в которой всякий переход между двумя состояниями одной системы должен сопровождаться неким переходом между двумя состояниями какой-то другой системы. На общепринятом языке это соответствует процессам излучения (поглощения) одной системой и поглощения (излучения) другой системой.

• 10.    На основе алгебраических соображений бинарной предгеометрии строится теория атомов, соответствующая общепринятой квантовой механике.

3.    Реляционно-статистическая парадигма

(3,3) можно обосновать происхождение как размерности, так и сигнатуры наблюдаемого классического пространства-времени.

Бинарная предгеометрия, охарактеризованная выше, является лишь предгеометрией, поскольку на ее основе строятся лишь прообразы общепринятых классических пространственно-временных отношений. Аналогичное можно сказать и про понятия из физики микромира. В предгеометрии микрочастицы описываются лишь наборами комплексных чисел (компонентами спиноров), тогда как в квантовой механике частицы описываются комплексными (спинорными) функциями. Для перехода от бинарной пред-геометрии к общепринятым понятиям необходимо учесть (осмыслить) следующие 5 видов соображений.

• 1.    Прежде всего, следует учесть принцип Маха, причем в более широком смысле, нежели его формулировал А. Эйнштейн. Напомним, Эйнштейн его понимал как обусловленность значений масс и инерции глобальными свойствами окружающего мира (Вселенной). Однако, в работах ряда авторов, в частности Р. Фейнмана и Дж. Уилера [11] принцип Маха трактовался шире. В их работах было предложено устранить опережающие взаимодействия путем учета влияния со стороны всего окружающего мира на две взаимодействующие частицы (системы). При этом, заметим, речь шла об устранении именно электромагнитных опережающих воздействий. Будем трактовать принцип Маха как обусловленность локальных свойств рассматриваемых систем глобальными свойствами окружающего мира.

• 2.    Другой вид соображений известен как идея о макроскопической природе пространства-времени. Так, П. К. Рашевский в своей классической монографии “Риманова геометрия и тензорный анализ” писал: «Между тем трудно сомневаться в том, что макроскопические понятия, в том числе и наши пространственно-временные представления, на самом деле уходят своими корнями в микромир. Когда-нибудь они должны быть раскрыты как некоторый статистический итог, вытекающий из закономерностей этого мира - далеко еще не разгаданных - при суммарном наблюдении огромного числа микроявлений» [12, c. 258]. Близкую точку зрения высказывал американский физик-теоретик Е.Дж. Циммерман. Можно еще привести высказывания в этом же духе Р. Пенроуза и других авторов. Однако, как правило, авторы не указывают конкретную природу суммируемых факторов.

• 3.    Напомним соображения, высказанные рядом авторов по поводу статистической природы квантовой механики. Так, А. Эйнштейн писал: «Тот факт, что квантовая механика позволяет столь просто получить выводы, касающиеся прерывных переходов (кажущихся) из одного общего состояния в другое, не давая фактически представления об отдельных процессах, связан с другим фактом, а именно, что теория в действительности оперирует не с отдельной системой, а с ансамблем систем» [13, c. 55]. Близких взглядов придерживались Л. И. Мандельштам, Д. И. Блохинцев и ряд других авторов. Однако в этих работах либо не указывается, что собой представляет квантовый ансамбль, либо бывает трудно полностью согласиться с предложенными вариантами.

• 4.    К четвертому типу соображений отнесем фейнмановскую интерпретацию сущности принципа Гюйгенса. В своих “Фейнмановских лекциях по физике” Фейнман писал: «Дифрагированная волна выглядит так, как будто источником служит дырка в экране. Мы должны выяснить причину этого явления, ведь на самом деле именно в дырке нет источников, нет никаких зарядов, движущихся с ускорением» [14, c. 98]. И он дает ответ на этот вопрос, показывает, что на самом деле следует суммировать отношения между источником и реальными атомами решетки плюс отношения между атомами в решет-

• ке и точками на экране. Оказывается, в итоге получается тот же результат, но с обратным знаком: «Знак нас не интересует, поскольку обычно имеют дело с интенсивностью, пропорциональной квадрату поля». Однако при этом возникает вопрос: названные отношения только ли влияют на результат конкретного эксперимента, или играют еще какую-то роль? Если играют какую-то роль, то нужно будет иметь в виду, что вокруг нас имеется “море” испущенного излучения. . .

• 5.    Далее приведем соображения, высказанные в диспутах в Ленинградском политехническом институте на рубеже 20-х — 30-х годов. На этих диспутах, в которых участвовали виднейшие физики страны, обсуждался вопрос о выборе одной из двух концепций - близкодействия или дальнодействия. Основными докладчиками были Я. И. Френкель, который отстаивал концепцию дальнодействия, и В. Ф. Миткевич, выступавший сторонником концепции близкодействия. Миткевич задал Френкелю ключевой вопрос: Пусть излучатель А испустил фотон, который через десять лет поглотит система В. «А в промежутке в течение десяти лет, где находится излученная энергия, где находится физический агент, который должен в конце концов воздействовать на приемник В?» [15, с. 55]. Френкель, отвечая Миткевичу, говорил, что энегию испущенного фотона можно считать распределенной во всем пространстве. Этот ответ был не в полной мере соответствующим реляционному подходу, поскольку в нем пространство время не является самостоятельной категорией, а выводится из более фундаментальной категории отношений.

4.    Энергия излучения и прообраз закона Хаббла

Практически все упомянутые авторы рассуждали, считая априорно заданным пространство-время. Однако, поскольку в реляционном подходе нет самостоятельной категории пространства-времени, а вместо него выступает совокупность отношений между материальными объектами (зарядами), кроме того имеется “ море ” испущенного, но еще не поглощенного электромагнитного излучения, то возникают веские основания высказать идею, совмещающую в себе все пять упомянутых видов идей: следует считать, что испущенное, но еще не поглощенное электромагнитное излучение участвует в формировании самой идеи пространственно-временных отношений. Более того, можно высказать даже еще более сильное утверждение, что именно испущенное, но еще не поглощенное электромагнитное излучение, ответственно за формирование понятий классического пространства-времени [3] .

Неким подкреплением данной идеи может служить мысль, высказанная в середине ХХ века нидерландским математиком Д. Ван Данцигом: « Можно считать метрику описанием некоторого “ нормального ” состояния материи (включая излучение) и дать ей статистическую интерпретацию, как некоторое усреднение физических характеристик окружающих событий, вместо того чтобы класть ее в основание всей физики » [16] . Ван Данциг явно называл факторы, которые « обуславливают стремления к построению более реалистичной модели физики, так называемой “ модели вспышек ” , где материя представляется в виде конечного числа конечных групп элементарных событий, называемых вспышками, где конечные группы представляют импульс энергии, а также пространственно-временные отношения » . Эта идея созвучна сформулированной выше, если под вспышками понимать испущенное, но еще не поглощенное электромагнитное излучение.

Применим изложенные соображения реляционно-статистической парадигмы к описанию космологии. Во Вселенной, как системе большого числа массивных излучателей и поглотителей, сказанное выше приводит к двум следствиям:

• 1.    Относительно любого наблюдателя все окружающие его объекты должны восприниматься, как обладающие некой дополнительной энергией.

• 2.    Наблюдаемые расстояния до окружающих объектов, вообще говоря, отличаются от классических (архимедовых).

В контексте первого следствия можно говорить о распределении испущенной энергии по всем возможным поглотителям. Таким образом, наблюдаемым поглотителям будут приписываться некоторые скорости, направленные в сторону от наблюдателя (поскольку реальное поглощение всегда приводит к отталкиванию). Более конкретно это означает, что плотность энергии электромагнитного излучения должна совпадать с плотностью энергии наблюдаемого “расширения” Вселенной, по крайней мере в той области, где закон Хаббла линеен. В предыдущей работе авторов [17] было показано, что эти величины действительно совпадают в указанной области. Здесь мы лишь кратко напомним полученный результат.

Полная плотность электромагнитного излучения определяется двумя факторами: реликтовым излучением и прочим излучением звезд. На основании данных телескопа “ Планк ” [18] о температуре реликтового излучения величина первого вклада вычисляется с большой точностью:

£ ,е(

P rel = . 2

^4cq = (4 . 644 ± 0 . 004) X 10 - 34 二, С 3                                см 3

где ст = 5.6686 X 10 ^{- 5}

эрг · с · К ⁴ _–

см ²

всех звезд во Вселенной известна с [19, c. 371]:

постоянная Стефана-Больцмана. Плотность энергии излучения меньшей точностью. Впервые ее оценку произвел А. Эддингтон

„ . 8 . 58 ^{X 10 - 34} 焉.

В итоге, полная плотность энергии излучения во Вселенной может быть оценена величиной

г

^{P rad} = ^{P rel} + ^{P star} - ^{32 X 10}    см 3 .

Теперь оценим энергию “ расширения ” материи во Вселенной. На основании современных наблюдательных данных мы можем с достаточной уверенностью рассуждать о плотности материи и ее движении лишь в ограниченном объеме пространства (в котором закон Хаббла линеен). По результатам Supernova Cosmology Project [20] это ограничение соответствует красному смещению, начинающемуся с ， ° 〜 0.1. Скорости разбегания галактик и их скоплений в этой области существенно меньше релятивистских, поэтому энергию можно выразить формулой:

Е = / 三 dV = 4 亓 / 户呼办 =2^р _т Я 2 Я ⁵ ,

где скорость определяется законом Хаббла 。 = %『 .Будем учитывать только наблюдаемую материю, для которой отношение плотности к критической составляет Q ^ = 0 . 0456 士 0 . 0016 [21] . Заметив, что из закона Хаббла R/Rh = z, находим для плотности энергии расширения:

Р енр = 10 ^z 2 ^Q b 8|| ^- (1.2 士 0.31) ^{X 10 - 33} см 3 , (6)

где G = 6.672 X 10 ^{- 8} гравитационная постоянная Ньютона.

Таким образом, плотность энергии расширяющейся Вселенной ( 6 ) совпадает с плотностью энергии электромагнитного излучения ( 4 ), что подтверждает справедливость данной выше реляционной интерпретации процесса космологического “ расширения ” Вселенной.

Этот результат можно представить иначе, проведя обратное рассуждение: вычислить параметр Хаббла из условия равенства суммарной энергии излучения энергии наблюдаемого “ расширения ” в заданном объеме. Тогда % оказывается равным:

% = /0ІГ - 2.34 X 10 ^{- 18} с ^{- 1} - 72.21 Мк.

Однако заметим, что условие равенства энергий предполагает усреднение по довольно большому объему наблюдаемого пространства, и из него нельзя получить закон Хаббла как таковой. Для того, чтобы это сделать, нужно рассматривать энергию испущенного, но не поглощенного излучения, в ограниченном объеме между наблюдателем и наблюдаемым гравитационно-связанным объектом (галактикой или скоплением галактик).

5.    Линейный закон Хаббла

Пусть наблюдаемый объект имеет поперечный размер Аг, массу М и находится на расстоянии г от наблюдателя. В соответствии со сказанным выше, средний импульс испущенного, но не поглощенного излучения, приходящийся на площадку Аг ² , будет равен:

^{rad > =}3 ^ =3 …* 『 •

Тогда в нерелятивистском приближении, которго вполне достаточно для г < 0.1, наблюдаемая скорость удаления объекта от наблюдателя будет

V

pradcAr2

----------------r.

3М ,

а его красное смещение

г

p ,od Ar ² 3M "

то есть линейно по r в ведущем порядке. Причем, коэффициент перед расстоянием

P rad c Ar» 3М

三 Я(М, Ar),

зависящий как от плотности излучения, так и от характеристик наблюдаемого объекта, должен быть близок к параметру Хаббла Я ° .

Оценим величину Я(М, Ar) для среднего скопления галактик, имеющего поперечный размер Ar t 10 26 см и массу М t 10 47 г. Будем иметь:

Я(М, Ar) t 1.3 X 10 - 18 с ^{- 1} ,

что по порядку совпадает с ( 7 ). Поэтому можно ожидать, что при усреднении по всем скоплениям галактик, скорости которых далеки от релятивистских, окажется

<Я (М, Ar) > 〃 , △ 『 = Я о .

Это означает, что параметр Хаббла в космологическом смысле представляется как результат усреднения по всем гравитационно-связанным объектам в большом объеме Вселенной, но так же имеет смысл и для каждого из них в отдельности.

6.    Нелинейная часть закона Хаббла

Для объектов с г > 0.1 мы уже не можем строго следовать рассуждениям, используемым в предыдущем параграфе, главным образом потому, что скорости “ убегания ” приближаются к релятивистским. Для того, чтобы, следуя реляционному подходу, получить закон Хаббла за пределами указанной области, обратимся ко второму следствию в начале четвертого параграфа и еще одной важной идее.

Пространственные координаты, которые получаются в теории БСКО, являются компактифицированными (с точностью до целого числа длин волн). На основе идей, описанных в параграфе 3 можно сделать вывод, что компактификация устраняется учетом всей совокупности вкладов испущенного, но не поглощенного излучения. Свойство двойственности БСКО, описанное в п. 8 параграфа 2 позволяет высказать гипотезу, что поскольку в пространстве скоростей существует предельное значение – скорость света с, то при конечном числе излучателей-поглотителей пространственные координаты во Вселенной могут быть так же ограничены неким предельным расстоянием.

Данная гипотеза дает обоснование идее П. К. Рашевского, сформулированной им в статье “О догмате натурального ряда” [22], где он указал, что нет никаких оснований полагать, что «пересчеты как угодно больших расстояний в физическом пространстве и т.п. должны подчиняться существующим схемам натурального ряда и числовой прямой». Идея приобрела конкретную реализацию в работах В. Л. Рвачева [23, 24], где был введен измененный закон суммирования расстояний, который соответствовал релятивистскому закону сложения скоростей:

о

r * 1 + r * 2 =

L * 1 + Г * 2 1 + Q ² Г * 1 Г * 2

где 1 /q = R 0 — максимальное расстояние. При этом, функция, осуществляющая отображение из поля с максимальным расстоянием в поле действительных чисел (г = т(г * ) : R т R) представляется в виде

丁 (г * ) = In ^{- 1}

1 + Q

1 - Q

In (

1 + Qr *

1 - Qr *

)•

На этой основе Рвачев построил так называемую неархимедову арифметику, заменив все операции релятивистскими, ввел элементарные функции в неархимедовых числах, определил производные и интегралы. И, что наиболее важно для нас, Рвачев показал, что во Вселенной с неархимедовыми расстояниями, удаленные объекты автоматически будут иметь красное смещение в своих спектрах [24] .

Для вычисления космологического красного смещения будем использовать технику Рвачева, более подробно описанную в работе [25] . Рассмотрим излучение, испущенное наблюдаемым объектом 6 на расстоянии г * от наблюдателя. Пусть А ₁ — длина волны испущенного излучения. Тогда в точке, где находится наблюдатель а, она будет равна Л ₂ = т(г * + А ₁ ) — т(г * ) ( Рис. 1 ).

При А ₁ 《 г * отношение 人 ₂ /Х ₁ переходит в производную функции т:

1 + 2 = А 2 = R* ^{+А 1 ) — Т}О т т ‘ (г * ). ^А 1               ^А 1

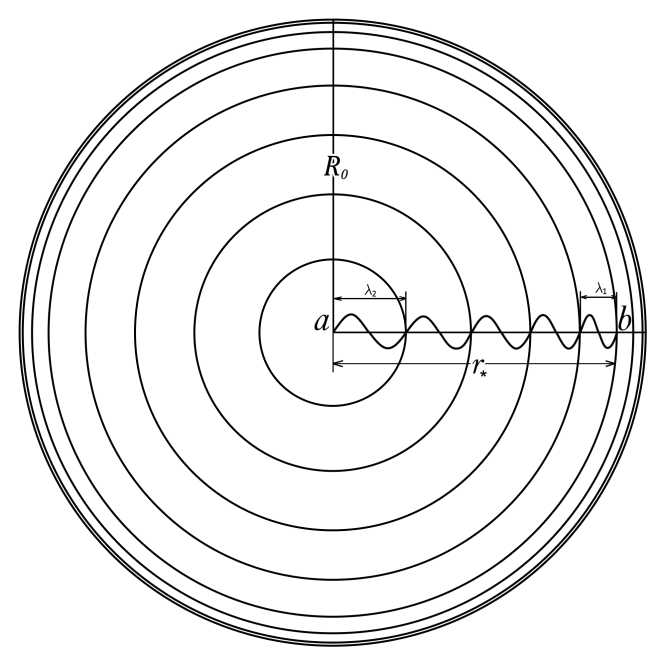
Рис. 1. Вселенная с точки зрения наблюдателя а

Нетрудно убедиться, что производная равна т '"т—1^ •

С точностью до членов второго порядка по г * /А о для красного смещения получим

N = 丁 ' (г * ) — 1

,

где мы учли, что при г * 《 冗 о можно заменить г * на г. То есть в ведущем порядке космологическое красное смещение, обусловленное указанной неархимедовостью расстояний, оказывается квадратичным по г.

7.    Оценка параметра замедления

Остается вопрос, каким должно быть максимальное расстояние 冗 о ? На первый взгляд, можно было бы взять в качестве этой величины радиус Хаббла Rh = с/Н о t 1.3 х 10 ²⁸ см. Однако, как мы выяснили ранее, линейный закон Хаббла, содержащий Н о , выполняется в ограниченной области пространства, а квадратичная часть, полученная в этом пункте, имеет смысл для всей наблюдаемой Вселенной и на больших расстояниях вносит решающий вклад. Поэтому более естественным представляется выбор другой величины.

Поскольку масса наблюдаемой Вселенной (масса метагалактики) конечна, то соотношение Маха задает конечный гравитационный радиус

2GM

Модельно-независима я3 оценка этой массы составляет M 〜 10 56 г [26] , поэтому гравитационный радиус R g t 1.5 х 10 ²⁸ см. Он имеет тот же порядок, что и R h , но, вообще говоря, не совпадает с ним, а содержит некоторую поправку. Выбор R g в качестве максимального расстояния наиболее естественен, поскольку эта величина определяется всей наблюдаемой материей, а не привязывается к какому-либо ограниченному объему. Кроме того, это в полной мере согласуется с неотъемлимой частью реляционного подхода — принципом Маха.

Теперь сравним формулу ( 18 ) при R 。 = R g с квадратичной частью закона ( 1 ) и найдем параметр замедления:

Q o t 2

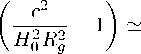
— 0.5,

что хоть и не является точным результатом, но оказывается близко к наблюдаемому значению [6]

g o = — 0.53 - 0 . 13 .

8.    Обсуждение и выводы

В рамках реляционного подхода удается обосновать обобщенный закон Хаббла ( 1 ) и сделать оценки космологических параметров ( 7 ) и ( 20 ), которые совпадают с данными наблюдений и при этом не требуют введения в теорию ненаблюдаемых видов материи.

Таким образом, реляционный подход оказывается весьма перспективным не только для описания процессов, происходящих в микромире (см., напр. [3, ч. III]), но и позволяет довольно точно описывать наблюдаемые эффекты в масштабе Вселенной.

Напомним, что в данной работе все оценки проводились на основе усредненных данных об излучении и веществе во Вселенной, то есть, в частности, полагалось, что все расстояния декомпактифициро-ваны, а использование модифицированных координат Рвачева, фактически, осталось необоснованным. В этой связи заметим, что аппарат БСКО представляет возможность такого обоснования (а быть может и уточнения) и позволяет более последовательно построить модель, которая бы адекватно описывала наблюдаемое космологическое красное смещение, основываясь на рассмотрении элементарных процессов испускания и поглощения электромагнитного излучения атомами. Однако это является более сложной задачей, и настоящая работа показала, что есть все основания приступить к ее решению.

Тем не менее, по итогам данной работы возникает ряд вопросов об интерпретации полученных результатов и/или экспериментальных данных. Главным вопросом является: действительно ли Вселенная расширяется, или эффект ее расширения следует считать кажущимся наблюдателю? В параграфе 4 рассмотрен усредненный вклад в красное смещение испущенного, но не поглощенного излучения, который соответствует импульсному каналу БСКО, и поэтому обычно интерпретируется как эффект Доплера. Однако, этот эффект не является наблюдаемым в явном виде, поскольку “ наблюдение ” всегда означает “ поглощение ” , а вклад процессов поглощения должен соответствовать координатному каналу, то есть приводить к изменению наблюдаемых координат объектов. В итоге, следуя приведенным рассуждениям, оказывается невозможным из наблюдений установить, приводит первый вклад к реальному расширению или нет.

В этой связи следует напомнить, что первая космологическая модель, полученная Эйнштейном на базе частного решения его уравнений, была статической. Кроме того, Вселенная в ней обладала конечной массой и имела радиус а = 2GТИ/ттс ² [27, с. 121]. Известно, что Эйнштейн, находясь под влиянием взглядов Спинозы, считал, что Вселенная существует вечно. В частности, по этой причине он на первых порах отвергал нестатические космологические решения, полученные А. А. Фридманом. Аббат Леметр обратил внимание на соответствие начальной сингулярности в решениях Фридмана иудейско-христианским представлениям о творении мира Богом. По свидетельству историков физики [28] , А. Эддингтон, которому Леметр изложил свои взгляды, ему сказал, что, может быть, так рассуждать и можно, но « Ваша идея отвратительна » .

Необходимо отметить связь примененных в данной работе неархимедовых координат г * с измененными координатами, использованными в работе М. Ю. Ромашки [29] . В этой работе они вводятся, следуя тем же идеям Рашевского и Рвачева, при построении реляционного варианта модифицированной ньютоновской динамики (MOND) для описания наблюдаемых кривых вращения галактик. При этом удается не только полностью исключить темную материю из описания экспериментальных данных, но и получить правильный закон отклонения лучей света удаленными галактиками и их скоплениями. Введенная связь измененных координат с обычными архимедовыми отличается от указанной здесь в формуле ( 15 ), хотя имеет схожие асимптотики. Несомненно, такая взаимосвязь представляет большой интерес, кроме того, она ставит вопросы о новой интерпретации с позиций реляционного подхода константы ускорения а ° , обнаруженной в MOND. Как пишет автор MOND М. Милгром [30] « Это приблизительно то ускорение, которое нужно объекту, чтобы разогнаться от состояния покоя до скорости света за время существования Вселенной. Также оно близко к недавно обнаруженному ускорению Вселенной 4» .

За рамками настоящей работы остается еще много вопросов современной космологии.