Обобщённое контактное число плоскости для нескольких слоёв

Семейство шаров в R называется упаковкой, если никакие два из них не имеют общих внутренних точек, но могут касаться друг друга. В данной статье мы ограничимся лишь конечными упаковками дисков единичного диаметра и соответственно будем опускать уточнение «единичного диаметра».

Одним из понятий, связанных с локальной структурой упаковки шаров, является контактное число. Напомним, что контактным числом пространства R называется наибольшее число d-мерных шаров одинакового размера без общих внутренних точек, которые могут касаться данного шара того же радиуса.

Легко заметить, что контактное число плоскости равно 6. Одним из классических вопросов математики является задача о 13 сферах, сформулированная в споре между Исааком Ньютоном и Дэвидом Грегори. Вопрос заключается в том, равно ли контактное число трёхмерного пространства 12 или 13. Впервые эта задача была решена К. Шютте и Б. Л. Ван дер Варденом в [3], где они показали, что контактное число трёхмерного пространства есть 12.

Л. Фейеш Тот и А. Хеппеш [5] рассмотрели обобщение задачи о контактном числе. Пусть дан шар и семейство шаров того же размера, касающихся исходного. Добавим ещё одно

семейство шаров того же размера, касающихся хотя бы одного из уже имеющихся. Никакие два шара в полученном наборе не могут пересекаться по внутренности. Найти наибольшее число шаров Тд, не считая исходного, в полученном наборе. Фейеш Тот и Хеппеш доказали некоторые нижние оценки для Т2, Т3 и Т4; в частности, что Т2 = 18. 3. Фюреди и П.А. Лёб [2, последний абзац раздела 6] приписывают Л. Фейеш Тоту и А. Хеппешу следующую гипотезу: Всякая подобная конфигурация для трёх слоёв на плоскости содержит не больше 36 дисков, не включая исходного. Эта гипотеза доказана в [4].

Введём формальные определения. Для любых двух дисков А и В унаковки Р назовём контактним расстоянием между А и В такое наибольшее п, что найдётся последовательность дисков Do, Di, ..., D_n Е Р, для которой А = Do, В = D_n, и любые два диска D— и Di касаются друг друга. Скажем, что упаковка Р имеет контактний радиус п, если найдётся такой диск D Е Р, который мы будем называть неходким, что контактное расстояние между диском D и любым друг им диском из Р не превосходит п. Обозначим через /(п) наибольшее возможное число дисков в упаковке с контактным радиусом п.

Гексагональная упаковка дисков даёт нижнюю оценку /(п) > 3п(п + 1) + 1, см. рис. 1. Поскольку контактное число плоскости равно 6, мы имеем /(1) = 7. Согласно [5], имеет место равенство /(2) = 19. Также известно [4], что /(3) = 37. Мы докажем следующую теорему.

Теорема 1. /(п) = (1 + о(1))

2тт ₉ —= п².

V3

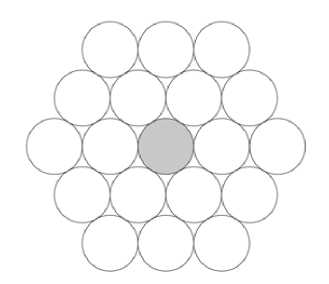
Рис. 1. Пример гексагональной упаковки с двумя слоями

В следующей секции сначала покажем справедливость приведённой верхней оценки на /(п). Затем введём определение (а, Ь)-меяъниуи и, наконец, покажем, как с помощью мельниц построить упаковки, дающие желаемую нижнюю оценку обобщённого контактного числа.

2.    Асимптотически наибольшая упаковка2.1.    Верхняя оценка

Рассмотрим произвольную упаковку Р_п с контактньім радиусом п. Будем считать, что её исходный диск находится в начале координат. Тогда легко видеть, что для всякого диска D Е Р_п с центром с выполнено |с| < п. В самом деле, если (0 = со,сі,...,с_п = с) есть последовательность центров дисков Р_п, где любые два соседних диска касаются друг друга, то п

|с| = |с - 0\ < ^ \с - Ci-1\ = п.

i=1

Таким образом, размер упаковки Р_п ограничен сверху наибольшим числом точек, которые можно расположить в круге радиуса п таким образом, чтобы все расстояния между точками были не меньше 1.

Теорема 2. (Олер, [1, Теорема 1]). Пусть Х — выпуклое компактное подмножество плоскости. Обозначим через Р (X) и А(Х ) соответственно периметр и площадь X. Обозначим через р(Х ) размер наибольшеео подмножества в X, в котором любые две точки находятся на расстоянии хотя бы 1. Тогда

р(Х ) <^—-А(Х ) + 1 Р (Х) +1. V 3         ²

Из теоремы 2 следует, что

УР4 <  —= • "//² + | • 2ттп + 1 = (1 + о(1)) • V 3       ²

^п2. Va

Ниже мы построим упаковки размера (1 + о(1)) • 2ттп2/V3.

2.2.    Мельницы

Для произвольного ненулевого вектора г будем обозначать через СгДг) единичный вектор того же направления, то есть

Сгг(г) = j^.

Пусть а > 3 и Ь > 1 — два натуральных числа. Рассмотрим следующую упаковку: - а дисков расположены по кругу таким образом, что любые два соседних диска касаются друг друга. Более точно, центры этих дисков находятся на окружности радиуса 1/(2 sin(7г/а)) и делят эту окружность на равные дуги. Обозначим через о центр данной окружности. Назовём эти а дисков центральными.

• -    Рассмотрим произвольный центральный диск D. Обозначим его центр через с и положим г = Сгт(с — о). Добавим ещё (Ь — 1) диск с центрами в точках с + г, с + 2г, ... , с + (Ь — 1)г. Все аЬ дисков, которые были построены до этого момента, будем называть каркасом. Набор {с + гг : 0 <  г < Ь} будем называть лучом каркаса, соответствующим диску D.

• -    Пусть сі — центр одного из центральных дисков Di, а с2 — центр другого центрального диска D2, следующего за первым против часовой стрелки. Как и в предыдущем пункте, положим гі = сИ'г(сі — о) и Г2 = Сгг(с2 — о). Обозначим через S область, ограниченную четырёхугольником с вершинами в сі, с2, с2 + (Ь — 1)г2, сі + (Ь — 1)щ. Неформально говоря, S есть пространство между двумя соседними лучами каркаса.

Обозначим через П2 вектор, отличающийся от г2 поворотом на тт/3 по часовой стрелке. Для всякой пары целых чисел (г,з ) обозначим dij = с2 + гг2 + 3U2. Если выполнены следующие условия:

• •    г > о,

• •    з > 1,

• •    г + з< ь — 1,

• •    dij G S,

• •    диск единичного диаметра с центром в dij не пересекается ни с каким диском каркаса, то добавим единичный диск с центром в dij в упаковку.

2.3.    Построение желаемой упаковки

Множество дисков, добавленных на этом шаге, вместе с лучом каркаса, соответствующим диску D2, назовём лопастью, соответствующей диску D2. Добавим аналогичные наборы дисков для каждой пары соседних центральных дисков.

Полученную упаковку, состоящую из а центральных дисков, других а(Ь — 1) дисков каркаса и оставшихся дисков всех а лопастей, будем называть (а, Ь)-мелъницей. На рис. 2 можно увидеть некоторые примеры мельниц.

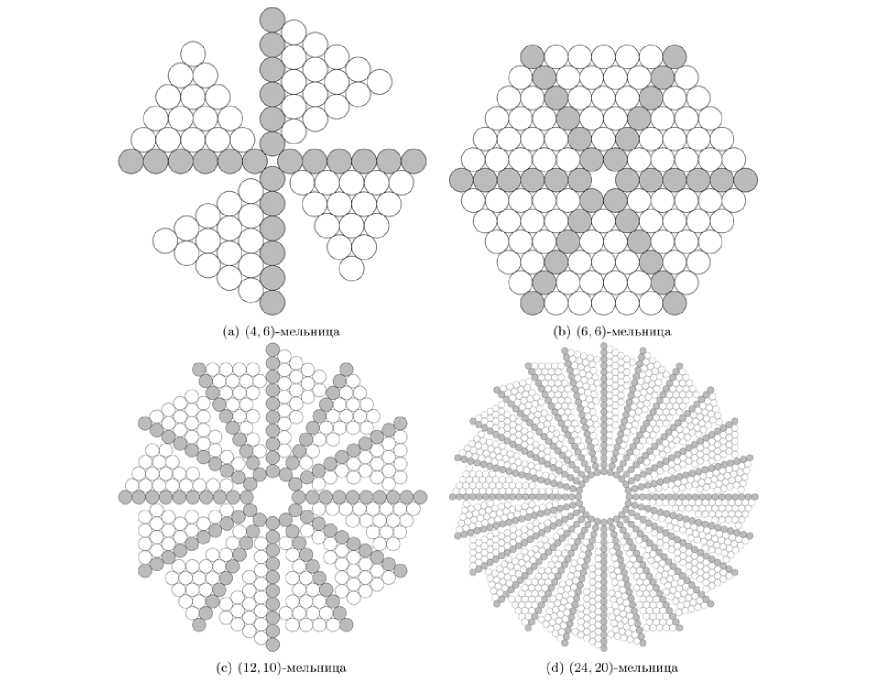
Рис. 2. Примеры мельниц. Для наглядности каркас окрашен в серый цвет

Рассмотрим произвольное п > 36. Возьмём ([уДДп — [уДJ)-мельницу в качестве упаковки 'Р,,: исходным диском этой упаковки назначим любой из центральных дисков мельницы. Мы утверждаем, что такая упаковка удовлетворяет нашим требованиям. Для удобства положим а = [y^J и b = п — а (таким образом, наша упаковка есть (а, b)-мeльницa).

Утверждение 1. В упаковке Р_п от исходного диска можно дойти до любого другого за п шагов.

Доказательство. В самом деле, от всякого центрального диска можно дойти до любого диска соответствующей ему лопасти не более чем за b шагов, по построению лопасти. От исходного диска можно дойти до всякого центрального диска не более чем за а шагов (и даже за (a/2j), поэтому от исходного диска можно дойти до любого другого не более чем за а + b = п шагов.

2л 9

—= п2.

Д3

Утверждение 2. |Р_П| = (1 + о(1)) •

Замечание Неформально говоря, это утверждение следует из того, что построенная упаковка состоит из лопастей, каждая из которых есть оптимальная упаковка некоторой области, и суммарная площадь таких областей есть (1 + о(1))лп².

Доказательство. Докажем, что каждая лопасть содержит (1 + о(1)) • —=п^3/2 дисков.

Пусть Di и D2 — два центральных диска, идущих подряд в таком порядке; их центры — соответственно ci и С2, и век торы щ и V2 определены так же, как и при построении лопасти, соответствующей диску D2. Как и при построении лопасти, обозначим через S четырёхугольник с вершинами в ci, С2, С2 + (b — 1)г?2, ci + (b — 1)щ.

Пусть p = С2 + (Ь — 1)^2. Рассмотрим следующий треугольник:

△ pqr = {ж 6 S : Zс₂pж < тг/3, dist(rr, [с1, С1 + (Ь — 1)v1 ]) > 1}.

Здесь через dist(p, s) обозначено расетояние от точки р до отрезка s. Обозначим оставшиеся вершины этого треугольника таким образом, чтобы сторона pq лежала на отрезке [С2, С2 + (Ь — 1)^2]: СМ. рис. 3.

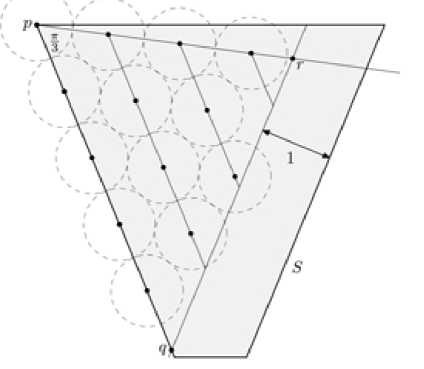
Рис. 3. Оценка, числа, дисков в лопасти

Пусть 7 = л/а. В частности. углы четырёхугольника S при сі іі С2 равны г/2 + 7.

Поскольку |с і — С2І = 1, легко убедиться, что

Sin 4       7

|q — С2| = 9----7------ = 7(1 + 0(1)) = °(1),

2 cos 7 cos 7   4

и, следовательно,

|Р — q| = (1 + о(1))|Р — С2| = (1 + о(1))(Ь — 1) = (1 + о(1))Ь.

Далее, поскольку векторы r — q и щ параллельны, получаем, что Zrqp = 2тг/а. Таким образом, если Һ есть длина высоты треугольника pqr. опущенная на сторону pq. то

һ =—74-27=d+"(и) 7=а+"а»—. ctg 1 + ctg 24 ctg 24 ^а

Проведём в треугольнике pqr отрезки, параллельные стороне pq, начиная с самой стороны pq, с промеж утками V3/2, как на рис. 3. Заметим, что для каждого такого отрезка длины I лопасть содержит хотя бы ^IJ дисков с центрами на этом отрезке, поскольку Zrqp = 2л/а <  л/3. и каждая тонка этого отрожа. представимая в виде С2 + 2^2 + JU2 из построения лопасти, удовлетворяет необходимым неравенствам на г и j' а конец каждого такого отрезка, лежащий на стороне pr, является центром диска, вошедшего в лопасть. Таким образом, число дисков, принадлежащих этой лопасти, не меньше, чем

⌊︁√2ℎ3⌋︁ ∑︁ г=0

Һ — г^2^ Һ

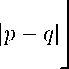
^⌊︁√ 2ℎ ₃ ^⌋︁

≥∑︁ г=0

Һ

-

7 V3Z ^г 21^1

Һ

≥

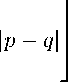
> (1 + "(1)) ?Һ •

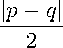
= (1 + "(1)) ^щСс "f1»

2лЬ2

V3>a

Таким образом, суммарное число дисков есть

,         , .. 2тгЬ2 .         . .. 2тгп2

(1+ О(1))— = (1 + 0(1))-^ , что и требовалось.

Таким образом, утверждения 1 и 2 показывают наличие упаковки Р_п, удовлетворяющей желаемой нижней оценке, и завершают доказательство теоремы 1.

Работа поддержана программой «Ведущие Научные Школы», грант НШ-775.2022.1.1.

Автор благодарит Андрея Купавского за упрощение конструкции, Александра Полянского за бесчисленные обсуждения и Андрея Сергунина за помощь в первом построении упаковки, лучшей, чем гексагональная.