Обоснование целесообразности выравнивания интервалов движения пассажирских транспортных средств регулярного сообщения на дублирующих участках

Вводная часть

Задача снижения количества и интенсивности использования личных легковых автомобилей довольно продолжительное время стоит на политической повестке дня многих стран из-за негативного воздействия автомобилизации на окружающую среду, человека и его здоровье [1– 3]. Достигается такое снижение посредством того, что водители начинают использовать более экологичные, экономичные и безопасные способы передвижения, как правило пассажирский транспорт регулярного сообщения. За по- следние годы проведено много научных исследований, целью которых является установление факторов, влияющих на выбор вида транспорта для поездок. Многие из этих исследований были сосредоточены на влиянии мер так называемой мягкой транспортной политики. Их цель – переориентировать владельцев автомобилей использовать для передвижения на иной вид транспорта. При этом цель достигается только путем убеждений и предоставления информации об экологически безопасных альтернативах, в первую очередь об услугах общественного транспорта [4, 5]. В то же время доказано, что если существующий уровень обслуживания на общественном транспорте не может конкурировать с автомобилем, то эффективность такой мягкой транспортной политики для уменьшения использования личных автомобилей ограничена [6, 7]. Следовательно, чтобы добиться более значительного сокращения количества автомобилей и частоты их использования, необходимо улучшать услуги общественного транспорта. Одним из способов повышения качества работы общественного пассажирского транспорта является опрос его пользователей – пассажиров с дальнейшей реализацией разработанных на его основе мероприятий.

Такой опрос был поведен в г. Гомеле (Республика Беларусь). Подробно реализация этапов его проведения изложена в [8], а результаты обобщены в [9–13]. На рисунках 1 и 2 соответственно приведены распределения частот предложений по совершенствованию транспортной системы г. Гомеля респондентов редко и часто пользующихся общественным транспортом.

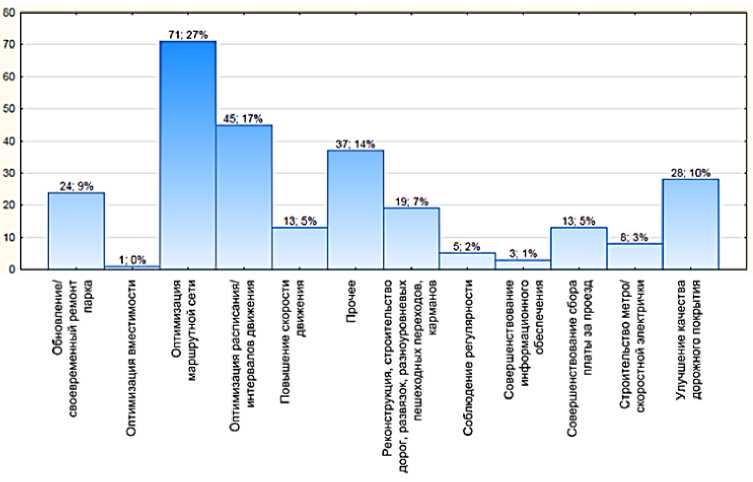
Рисунок 1 - Распределение предложений респондентов, редко пользующихся услугами общественного транспорта, по вопросу улучшения качества его работы

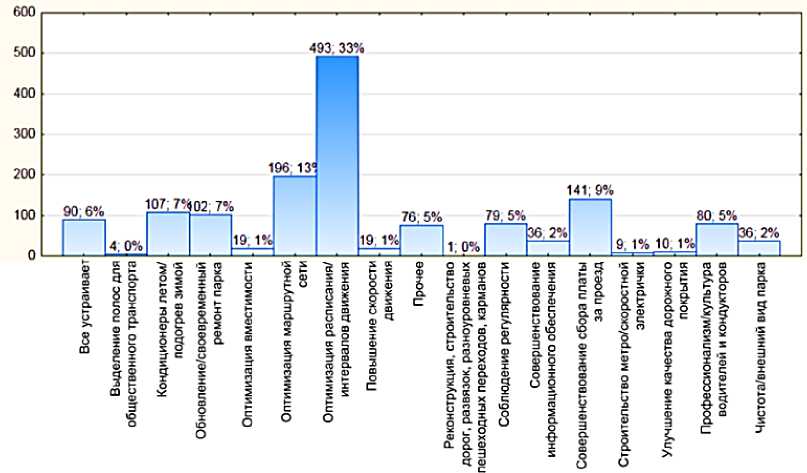
Рисунок 2 - Распределение предложений респондентов, часто пользующихся услугами общественного транспорта, по вопросу улучшения качества его работы

Рисунки 1 и 2 показывают, что наиболее значимым критерием для обеих категорий пользователей общественного транспорта являются вопросы оптимизации интервалов (расписания) движения. При этом следует иметь в виду, что категория предложений «Оптимизация интерва-лов/расписания движения» является обобщающей. Внутри этой категории респонденты предлагали различные обобщенные (например, «увеличить частоту работы автобусов») или конкретные (например «пустить дополнительный рейс по маршруту № 19, что бы успевать на работу на 6 утра») предложения. Для систематизации таких предложений респондентов внутри самой многочисленной их категории «Оптимизация интервалов/расписания движения», все они были сгруппированы по следующим подкатегориям:

• -    раньше начинать / позже заканчивать работу на линии;

• -    выровнять интервалы на дублирующих участках;

• -    согласовать расписание с вокзалами, предприятиями;

• -    уменьшить интервал движения.

На рисунке 3 приведено распределение ответов по этим подкатегориям суммарно для тех, кто часто и редко пользуется общественным транспортом.

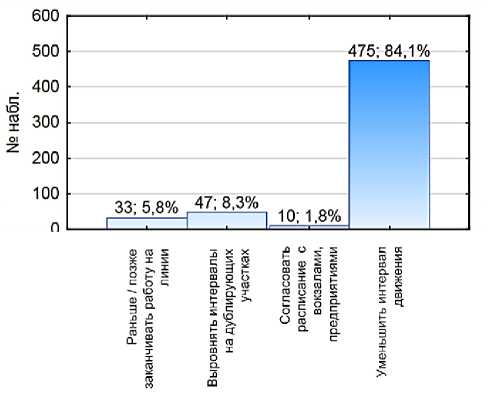
Рисунок 3 – Распределение ответа «Оптимизация интервалов/расписания движения» по подкатегориям

Из рисунка 3 видно, что наибольшее число пожеланий респондентов (84 %) относятся к уменьшению интервала движения, т.е. более частому движению пассажирских транспортных средств, что обеспечит пассажирам уменьшение времени ожидания на остановочных пунктах. Решение такой задачи на практике автобусов (троллейбусов), что неизбежно приведет к росту затрат на функционирование системы общественного транспорта. Такой рост крайне нежелателен в сложившихся условиях бюджетного финансирования работы общественного транспорта.

В тоже время представляется, что решение второй по значимости и приведенной на рисунке 3 проблемы (выровнять интервалы на дублирующих участках) в определенной степени позволит решить и вопрос уменьшения интервала движения (рисунок 4). Таким образом, цель данной работы – обосновать целесообразность выравнивания интервалов движения пассажирских транспортных средств на дублирующих участках маршрутной сети.

Основная часть.

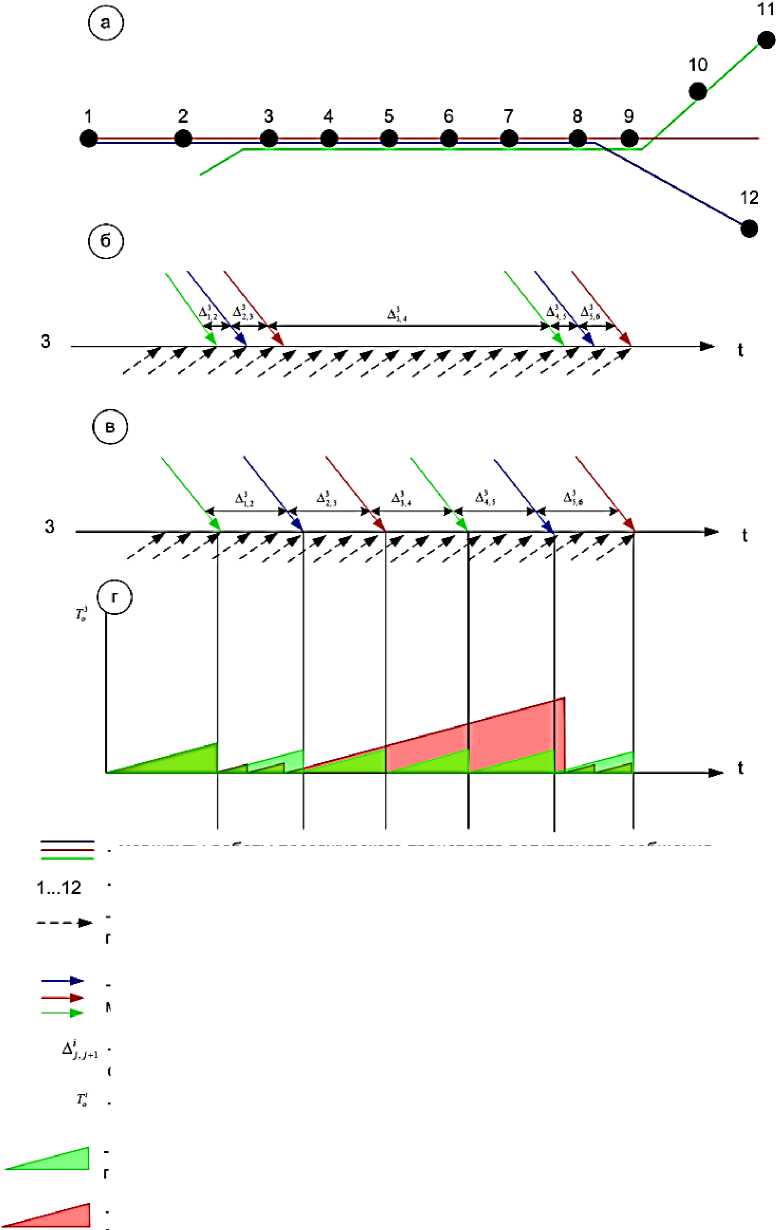
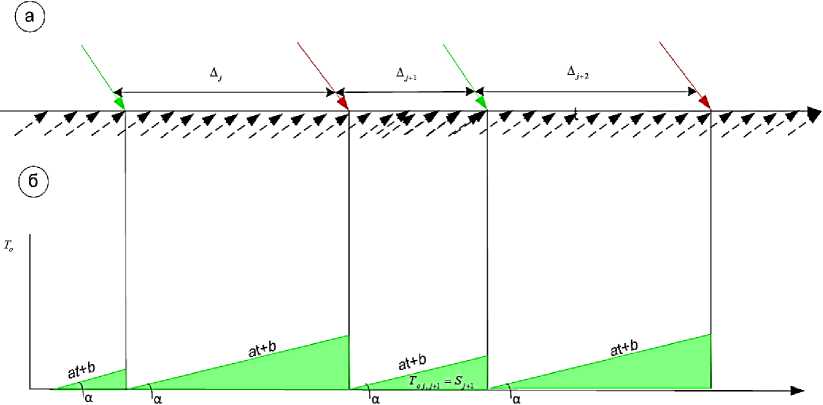
На рисунке 4, а приведена схема маршрутной сети, состоящая из трех маршрутов. На участке от 2 до 8 остановочного пункта два маршрута друг друга дублируют. Часть пассажиров, которые совершают посадку в k-м остановочном пункте (k е [2;7]) и пункт высадки которых l (l6 [3,8]) могут пользоваться для осуществления поездки транспортным средством любого из этих маршрутов. Аналогично и для участка от 3 до 8 остановочного пункта, по которому проходит три маршрута пассажирского транспорта.

На рисунке 4, б показано время прибытия на остановочный пункт 3 маршрутных транспортных средств трех проходящих через эту остановку маршрутов при несогласованном интервале их прибытия. В этом случае интервалы времени между прибывающими друг за другом маршрутными транспортными сред-

AL ствами ( j-j+1) не равны.

На рисунке 4, в показано время прибытия на остановочный пункт 3 маршрутных транспортных средств трех проходящих через эту остановку маршрутов при согласованном интервале их прибытия. В этом случае интервалы времени между прибывающими друг за другом маршрутными транспортными сред-д 3

ствами ( ^{j , j + 1}) равны между собой.

Для ситуации, изображенной на рисунке 4, б средний интервал движения будет равен k - I

_  ZA з Н, +1

. 3 н        j = I

A = -------- --- предполагает выпуск на линию дополнительных

k - ¹ . Где ^{A 3} " - математическое ожидание (среднее) интервалов прибытия маршрутных транспортных средств на остановочный пункт 3 при несогласованном расписании; k –

количество прибытия маршрутных транспортных средств всех маршрутов на остановочный A 3 H А пункт 3 за период времени Т; j,j+1 - интервал между j и j+1 транспортными средствами, пребывающими на остановочный пункт 3 при несогласованном расписании.

Для ситуации, изображенной на рисунке 4, в средний интервал движения будет равен k - I

_  za з с j +1

а 3 с = ——    —- k -1  . Где А с - математическое ожида ние (среднее) интервалов прибытия маршрутных транспортных средств на остановочный .  3 с

^А пункт 3 при согласованном расписании; ^{j , j + 1} -интервал между j и j+1 транспортными средствами, пребывающими на остановочный пункт 3 при согласованном расписании.

Поскольку в выражении ^{А 3} н и ^{А 3} с числитель равен одному и одному числу - периоду времени Т, и ра вн ы з наменатели, то можно утверждать, что ^{А 3} н = ^{А 3} с . То есть средние интервалы прибытия маршрутных транспортных средств на остановочный пункт в случае их согласованного или несогласованного прибытия будут равны.

На рисунке 4, г показано как изменяется время ожидания пассажирами на остановочном пункте при ожидании прибытия маршрутных транспортных средств при их согласованном (зеленый цвет) и несогласованном (красный цвет) прибытии. Очевидно, что угол наклона прямой к горизонтальной оси t показывает скорость накопления пассажиров на остановочном пункте. Зависеть эта величина будет от интенсивности прибытия пассажиров на остановочный пункт. Причем, чем выше интенсивность прибытия, тем больше угол наклона прямой к оси t . Также очевидно, что суммарное время ожидания пассажирами, прибывшими на остановочный пункт после отъезда рейса j и успевшими на рейс j + 1 ( Т о* ' * ^{+ 1}) будет равно площади соответствующего треугольника ( Sj +1 на рисунке 5).

Очевидно, что сумма времени ожидания пассажирами, которые могут ехать на любом из рассматриваемых маршрутов, на данном остановочном пункте и в данный интервал времени будет равна сумме всех площадей таких треугольников, т.е.

k - 1                k - 1               k - 1 I

• Т = у Т . = У 5 . =у - h b . оs               оj               оi                  j j

• j = ।            j = ।           j = । ²                     (1)

где к - количество прибытия пассажирских транспортных средств на данный остановочный пункт в рассматриваемый период времени, к >  2;

• h₁ - высота треугольника j;

• 6. - длина основания треугольника j.

• 6.    = ^j . ^j

А

При этом очевидно, что н, = А j tg а. Учитывая то, что, константа линейного уравнения показывает тангенс угла наклона этой прямой к оси абсцисс, можно записать tg а = а, где a - константа при переменной, описывающей интенсивность прибытия пассажиров на остановочный пункт. Тогда высота треугольника будет равна hj = а j a.                 (2)

Тогда выражение (1) примет вид:

Т о- = I Z I а ^А * ^А * = - Z | ^А 2                             ⁽³⁾

В случае, когда время прибытия транспортных средств разных маршрутов на один и тот же остановочный пункт не согласовано, интервалы прибытия будут раз н ыми и их значения

А = А ± a .        — будут определяться как j      А, где А - сред ний интервал прибытия пассажирских транспортных средств на рассматриваемый остановочный пункт в рассматриваемый период времени; aА - среднеквадратическое отклонение интервалов прибытия пассажирских транспортных средств на рассматриваемый остановочный пункт в рассматриваемый период времени. Тогда выражение (3) можно переписать в следующем виде:

k - I a

Т о- =- Х ( ^А± a А )            (4)

• ²   , = i

Очевидно, что при согласованном времени прибытия маршрутных транспортных средств на остановочный пункт среднеквадратическое отклонение интервалов прибытия будет равно нулю. Также, выше было показано, что математическое ожидание величины времени между прибытиями пассажирских транспортных средств на остановочный пункт не зависит от согласованности такого прибытия. Таким образом, доказав, что k -1                               k-1  

• - Z ( А± a А )² >  - Z ( А )² .     (5)

• 2 j = 1                         2 j = i

Можно доказать, что при согласованном прибытии пассажирских транспортных средств на остановочный пункт (когда интервалы между последовательно прибывающими транспортными средствами равны) суммарное время ожидания пассажирами на остановочном пункте будет меньше, чем при несогласованном прибытии. После упрощения выражение (5) можно записать в следующем виде:

a ( к - 2) -2    -        .

-----------( Д + 2 Д ст _к + ст „  +

ДД

Д - 2 Дст , + д

^ст Д ) >

a (к - 1) -2 ---------Д , 2

После упрощения добных можно получить:

и приведения по-

2       2             “2

2( к - 2)( Д + ст Д ) >  ( к - 1) Д ,

- маршруты работы пассажирского транспорта регулярного сообщения

- время ожидания пассажирами на остановочном пункте I, чел-мин

- время ожидания пассажирами на остановочном пункте при равных интервалах прибытия общественного транспорта

- прибытие на остановочный пункт маршрутных транспортных средств разных маршрутов

- время ожидания пассажирами на остановочном пункте при разных интервалах прибытия общественного транспорта

- интервал между транспортными средсствамиу иу+1, пребывающими на остановочный пункт /

- остановочные пункты

- прибытие на остановочный пункт пешеходов, успевающих к отправлению пассажирского транспортного средства

Рисунок 4 - Механизм снижения максимальных интервалов между прибывающими на остановочный пункт маршрутными средствами: а - схема маршрутной сети; б - неравномерные интервалы; г - равномерные интервалы; д - время ожидания пассажирами

---** - прибытие на остановочный пункт пассажиров

—► - прибытие на остановочный пункт маршрутных транспортных средств разных

|> маршрутов

-""' । - время ожидания пассажирами на остановочном пункте at+b - прямая показывающая интенсивность прибытия пассажиров на остановочный пункт

Рисунок 5 - Параметры, влияющие на величину времени ожидания пассажирами прибытия маршрутного транспортного средства: а – прибытие-отправление маршрутного транспортного средство на остановочный пункт; б – время ожидания пассажирами

Результаты

Из выражения (7) видно, что:

1 Для любого k > 3 будет справедливо не- равенство 2(k  2) > (k 1).

2 Для любых ¹ и ° ¹

будет справедливо

неравенство

²            2

( а + ° а ) >  а

Таким образом можно утверждать, что наименьшие потери времени пассажирами при ожидании прибытия маршрутных транспортных средств наблюдаются при равных интервалах движения между следующими друг за другом маршрутными транспортными средствами. Также видно, что с ростом среднеквадратического отклонения в интервалах времени между прибытиями пассажирских транспортных средств на остановочный пункт будет расти время ожидания пассажирами. Из этого следует, что при составлении расписания движения пассажирского транспорта нужно стремиться к минимизации разброса в величине интервалов между пребывающими друг за другом маршрутными транспортными средствами. Т.о. до- казано, что выравнивание интервалов на дублирующих (совместных для разных маршрутов) участках позволит обеспечить удовлетворение потребностей пассажиров, выявленных при проведении опроса (рисунок 3) в части уменьшения интервала движения.

Для оценки эффекта от оптимизации интервалов движения пассажирских транспортных средств регулярного сообщения на дублирующих участках предлагается использовать два показателя:

• 1    Абсолютное снижение времени ожидания пассажиром прибытия пассажирского транспортного средства:

а T = У ( Т - Т ₉.)

а ^ os 1 i os2i' , мин(8) i=i где o – количество остановочных пунктов в населенном пункте, для которого производится оптимизация интервалов движения;

• 1    – индекс, показывающий время ожидания пассажиром прибытия пассажирского транспортного средства до оптимизации расписания;

  2 – индекс, показывающий время ожидания пассажиром прибытия пассажирского транспортного средства после оптимизации расписания.

  2. Относительное снижение времени ожидания пассажиром прибытия пассажирского транспортного средства:

  
  

  o

  Δ T =

  отн

  i = 1

  
  

  ( Т ,   - Т ,

  os 1 i         os 2i

  
  

  Т

  os 1 i

  
  

  ■, %.

  
  

  После подстановки выражения (4) в уравнения (8) и (9) и их упрощения можно получить:

  
  

  ----2

  Л T a = a (k - 2)(( Л ,

  
  

  -

  
  

  -----2

  Л 2

  
  
  
  

  ²)) .

  
  

  этих коэффициентов принимаются равными единице. В результате этого возможны ситуации, когда ранг дублирующих участков будет одинаков (рисунок 6). Из рисунка 6 видно, что на представленном фрагменте маршрутной сети есть два дублирующих участка. На первом дублирующем участке три остановочных пункта, через которые проходят четыре маршрута. На втором дублирующем участке – три маршрута проходят через четыре дублирующих участка. Применение выражения (12) со значениями k оп и k м равными единице в данном случае даст одинаковые значения рангов обоих дублирующих участков, что не позволит обоснованно принять очередность оптимизации интервалов на них.

  
  

  Л T = 1 -

  отн

  
  

  -----2

  ^Л 2   +

  
  

  ^ Л 2

  
  

  Л ²   ,           2

  ^Л 1   + ^ Л 1

  
  

  Обсуждение и заключение

  В данной публикации показано, что выравнивание интервалов движения пассажирских

  
  
  

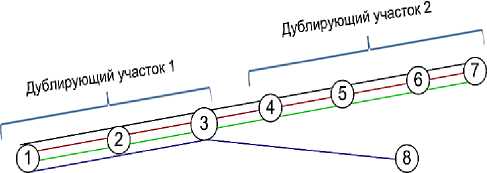
  Рисунок 6 – Пример фрагмента маршрутной сети

  
  

  транспортных средств приводит к сокращению времени ожидания их пассажирами. Для реализации такого выравнивания разработана и апробирована на ряде городов методика оптимиза-

  
  

  ции интервалов движения пассажирских транспортных средств регулярного сообщения [14– 16]. Эта методика предусматривает выделение в рассматриваемом населенном пункте дублиру-

  
  

  ющих участков, их ранжирование в порядке убывания значимости каждого из них, и после-

  
  

  дующую оптимизацию интервалов движения на каждом таком дублирующем участке, начиная с наиболее значимого, решением оптимизационной задачи о назначениях. При этом для ранжи-

  
  

  рования используется следующий показатель:

  
  

  R i = Q оп i

  
  

  ∙ k оп + Q м i ∙ k м .

  
  
  
  

  где

  
  

  i – номер дублирующего участка;

  
  

  R – значимость дублирующего участка,

  
  

  Q оп – количество остановочных пунктов в дублирующем участке,

  Q м – количество маршрутов в дублирую-

  
  

  щем участке,

  k оп – коэффициент значимости остановочных пунктов,

  k м – коэффициент значимости маршрутов.

  Очевидно, что в выражении (12) коэффициенты k оп и k м оценивают важность количества

  
  

  Кроме того, при апробации разработанной методики оптимизация велась для всех дублирующих участков населенного пункта. В тоже время очевидно, что при сдвиге интервалов в результате оптимизации, расписание меняется не только на данном дублирующем участке, где проводится оптимизация, но и на остальных участках, по которым проходят маршруты, вошедшие в дублирующий участок. В таких условиях можно предположить, что максимальное снижение времени ожидания пассажирами на остановочном пункте в целом для всего города будет достигнуто раньше перебора всех дублирующих участков.

  Таким образом дальнейшие научные исследования направления в данной сфере можно сформулировать следующим образом:

  • 1    Обоснование значений коэффициентов k оп и k м .

  • 2    Расчет итогового эффекта после оптимизации интервалов на каждом дублирующем участке и выбор варианта, обеспечивающего максимальное снижение времени ожидания пассажирами на остановочном пункте.

  
  

  остановочных пунктов и количества маршрутов соответственно. В настоящее время значения