Обоснование использования функций отклика при формализации задач экономического управления регионом
Автор: Лапшина М. Л., Лукина О. О., Горбунов В. В.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Экономика и управление
Статья в выпуске: 2 (84), 2020 года.
Бесплатный доступ
В настоящее время, в условиях самоизоляции, органы управления разного уровня, все большее внимание уделяют возможности использования экономических возможностей региона, с целью принятия наиболее адекватных управленческих решений, с наименьшими финансовыми потерями. На примере задач регионального развития показывается возможность практического использования функций отклика для координации экономических решений, позволяющей на основе свойств этих функций строить модель, дающую возможность анализировать объективные предпосылки координации планов в системе. Такая модель напрямую определяется целями согласования. Получение лучшего в каком-то смысле решения обязательно включает элементы координации. В экономических задачах это означает учет лимитированности природных ресурсов, созданных фондов и доступных капитальных вложений, трудовых ресурсов, способности к выживанию природы и т. д. Для учета таких факторов часто нужны достаточно громоздкие модели, описывающие специфику соответствующих отраслей народного хозяйства, промышленности, конкретных регионов. Согласование же решений, основанных на подобных моделях, представляет собой суперзадачу, которая сталкивается с проблемами размерности, разрывности и т.д. Поэтому необходим достаточно простой и универсальный способ приближенного согласования встречающихся на практике экономических (и аналогичных) задач. Работа состоит из 3-х частей: 1 - анализ существующих подходов в предметной области, 2 - непосредственная формализация исходной задачи, с обоснованием возможности использования имитационных моделей, использующих функцию отклика, 3 - основные выводы с их экономической интерпретацией. В работе представлен обзор литературных источников в предметной области, а также дана экономическая интерпретация полученных результатов.
Модель, оптимизационная задача, ресурсы, согласование, отрасли
Короткий адрес: https://sciup.org/140250932
IDR: 140250932 | УДК: 360 | DOI: 10.20914/2310-1202-2020-2-213-221
Текст научной статьи Обоснование использования функций отклика при формализации задач экономического управления регионом
Любое оптимальное решение означает согласование степени достижения цели с располагаемыми ресурсами. В этом смысле использование методов математического программирования можно рассматривать как инструмент согласования решений, в котором значимость всех ресурсов одинакова: нехватка любого из них ограничивает рост функции цели независимо от ценности ресурсов, суммы затрат по его дополнительному привлечению и т. д.
Большое распространение получили и методы согласования многоуровневых (в основном, двухуровневых) задач – декомпозиционный и синтетический, или композиционный. Основой первого служит разбиение общей модели системы на относительно независимые блоки в соответствии с принятой иерархией. Построение декомпозиционных схем начинается обычно с решения задачи верхнего уровня. Вырабатывается единый, поступающий «’сверху” сигнал, используя который можно получить несвязанные задачи, например, с модифицированными локальными целевыми функциями. Существует ряд модификаций этой схемы, базирующихся либо на конечных процедурах линейного программирования, либо на применении методов возможных направлений. Среди приближенных методов можно выделить процедуры, использующие функции отклика.
Например, в [1] ставилась задача согласования отраслевых планов размещения производства, для решения которой строилась так называемая функция отказа, показывающая изменение (приращение) отраслевых издержек при отказе от лучшего, с точки зрения отрасли, варианта размещения предприятия в данном пункте.
В дальнейшем алгоритм, построенный с помощью функций отклика как обобщенного описания реакции объекта на изменение внешних условий, был предложен в [2–3], где также рассматривалась задача размещения предприятий разных отраслей в составе промузла. Для увязки отраслевых решений предлагалось исследовать зависимости минимумов отраслевых издержек от мощностей предприятий в данном промузле. Приближенное построение таких зависимостей проводилось с использованием двойственных оценок отраслевых планов. Тогда задача сводилась к нахождению минимума суммы этих функций для всех отраслей и промузлов с учетом общесистемных ограничений. Задача решалась методом динамического программирования. Однако возможности этого метода сужаются с увеличением числа ресурсных ограничений. Дальнейшая разработка данного подхода рассмотрена в [4].
В последнее время функция отклика применяется многими исследователями проблем согласования экономических решений. Так, в [5–6] функции отклика вводятся как элемент имитационных систем, необходимый для формирования задачи согласования. При этом требуются сведения о функциях материальных издержек, капитальных и трудовых затрат и т. д. Все они имеют своим аргументом производственные задания по выпуску продукции и, с точки зрения имитационного подхода, являются функциями отклика подсистем нижнего уровня на координирующий сигнал, поступающий от управляющей системы верхнего уровня.
В [7] построение функций отклика основано на методике планирования эксперимента. Аппроксимация этих функций представляет собой уравнения многофакторной регрессии.
Рассмотренные примеры вычисления и применения функций отклика объединяются общей схемой [11]. Согласование решений в системе моделей с помощью функций отклика разбивается на два этапа. Сначала одновременно во всех подсистемах проводятся вариантные расчеты и строятся функции отклика. Затем в координирующем блоке модели отдельных блоков заменяются на их функции отклика и рассчитывается оптимальное решение системы.
Формализованное представление задачи
Ниже под функцией отклика понимается некоторое обобщенное описание реакции объекта на изменение внешних условий. Если отдельный блок системы описывается оптимизационной моделью, то функцией отклика может служить последовательность значения функционала при варьировании тех или иных параметров модели.
Рассмотрим систему, состоящую из нескольких независимых блоков (скажем, моделей, описывающих отдельные отрасли экономики региона). Пусть каждая из отраслевых задач ( k = 1,..., K ) описана оптимизационной моделью:
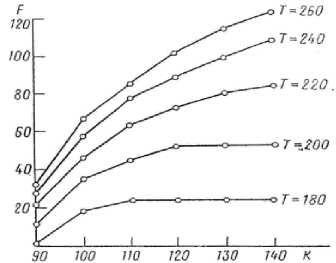
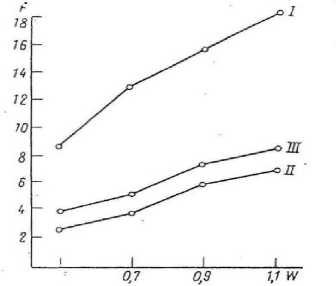
Найти max fk (Xk ), Xk e Bk, G^Xk ) < Rik , где X – вектор состояния подсистемы k, например, вектор выпуска продукции отрасли k; B – множество допустимых состояний блока k, определяемое его внутренними технологическими и ресурсными возможностями; G (Xk) < R - зависимость состояния отрасли от внешних условий, например, от наличия общесистемных ресурсов, R, i =1,..., m, ^R^ k В линейных и линейно-целочисленных задачах, которыми может быть описано большинство практических проблем оптимизации в экономике, функции fi (Xk) и Gi (Xk) удовлетворяют условиям выпуклости или по крайней мере монотонности. Общесистемные ресурсы (капитал, труд, вода) могут служить теми параметрами, которые являются аргументом функции отклика блока к на изменение общих условий функционирования системы [12]. Для построения функции отклика необходимо: исследовать область изменения каждого из параметров и их совокупности (область допустимости {Rk}); определить значения функционала задачи во всех или хотя бы в некоторых точках указанной области. Каждый из параметров Rk может меняться от наименьшей величины, ниже которой задача становится несовместной, до наибольшей, когда ее превышение уже не улучшает функционал. Поэтому область изменения параметров представляет собой параллелепипед в т-мерном пространстве параметров Rk< Rk< Rk, где Rk, Rk - минимальное и максимальное значения Rk .. Для приближенного описания функции отклика строится сетка изменения параметров, т. е. для каждого R k задается шаг его изменения ARk, величина которого выбирается эмпирически в зависимости от особенностей задачи. Проводя серию решений оптимизационной задачи (1) в точках построенной сетки, получим некоторую аппроксимацию функции отклика. Такая аппроксимация правомерна, если у функции отклика нет локальных оптимумов. Для многоэкстремальных задач этот подход также может быть использован, но необходима следующая “страховочная” процедура: а) на основе имеющейся исходной информации надо проанализировать сравнительную эффективность вариантов, входящих в решения, и определить разницу между наиболее и наименее эффективными из них; б) наряду с найденным оптимальным решением для данной точки сетки нужно исследовать и другие структурно отличные решения, значение функционала которых отличается не более, чем на величину вышеуказанной разницы, и найти лучшее из них. Но эта процедура требует увеличения времени расчетов и может быть оправдана лишь при желании получить весьма точное решение. Тем не менее, с ее помощью можно построить приближенные функции отклика для всех блоков системы. Напомним, что цель построения функций отклика состояла в том, чтобы на их основе сформулировать модель, описывающую процесс координации планов в системе. Модель координационной задачи зависит от цели согласования [13]. Если речь идет об оптимальном распределении общесистемных ресурсов между отраслями регионального хозяйства, то задача сводится к нахождению оптимума глобальной целевой функции k Ф = max £ fk (Ri ). R- k=1 Воспользуемся следующим приближенным методом нахождения оптимума. Рассматривая каждое значение функции отклика и сам вектор параметров как вариант развития отрасли k, можно сформулировать задачу целочисленного программирования, позволяющую выбрать наилучшее сочетание вариантов для всех блоков системы, с точки зрения общего функционала. Сформулируем более точно координационную задачу. Найти max V fkxkl xki i, k при V ajkxk.< rj,jeJ, i, k J 0 Vxk- = 1xk- =ъ * e Ik I1 k e K, где f k - значение функции отклика отрасли k для варианта i распределения ресурсов, i e Ik, aijk - величина ресурса j в варианте i для отрасли к, j e J, г e I, k e K, xki - целочисленная переменная, характеризующая выбор варианта i для отрасли к; R; - общесистемное ограничение на потребление ресурса j. В силу приближенности задания функций отклика, решение этой задачи будет также приближенным, причем точность его зависит от выбранной области допустимости параметров и “мелкости” сетки точек, аппроксимирующих эту область. Ясно, что выбор более мелкой сетки, увеличивая точность решения, приводит к росту размерности координирующей задачи. Выход может быть найден в построении итеративного процесса следующего вида. Как первое приближение к оптимуму примем решение координационной задачи с относительно “крупной” сеткой изменения параметров. На следующей итерации процесса в качестве области допустимости параметров для каждого блока берется окрестность решения, полученного на предыдущем шаге. В этой новой, более узкой, области повторяются расчеты по той же схеме, но с более мелкой сеткой, т. е. с уменьшенным шагом изменения параметров. Снова строятся функции отклика каждого блока системы в окрестности точки, которая выбиралась как наилучший вариант развития отрасли в координационной задаче. Таким образом, в окрестности первого приближения – более точное описание функций отклика. Ставится новая координационная задача, размерность которой не будет чрезмерно увеличиваться, так как область изменения параметров ограничена окрестностью первого приближения. Решение новой задачи дает более точное приближение к оптимуму системы. Затем процесс повторяется. Признаком прекращения итераций может служить повторение или близость решений на соседних шагах процесса. Особенности решаемых задач Разработка достаточно универсального приближенного метода согласования экономических решений вызывалась необходимостью практического решения задач координации решений в системе моделей регионального развития. Эта система изначально строилась с использованием следующих принципов. 1. Описание с помощью математических моделей всех основных сторон социальноэкономической активности в регионе. 2. Реализация модульного принципа построения системы с возможностью изменения ее структуры в зависимости от специфики проблем конкретного региона. 3. Применение для описания отдельных секторов региональной экономики обобщенных (унифицированных) моделей, позволяющих решать подавляющее большинство возникающих в этих секторах проблем. Возможность “настройки” таких моделей на особые, редко встречающиеся ситуации, путем их соответствующего дополнения и расширения. 4. Ориентация на максимальную автоматизацию подготовки исходной информации, проведения расчетов и анализа полученных решений. Исходным этапом разработки системы является создание отдельных ее блоков – моделей различных секторов региональной экономики. Остановимся подробнее на этом этапе. К настоящему времени разработано множество отраслевых моделей: производственных и производственно-транспортных, статических и динамических, одно- и многопродуктовых. Каждая из таких моделей “нацелена” на решение специфических проблем конкретной производственной системы и отражает ее наилучшим образом. Как правило, построенные для определенных отраслей модели используются либо одноразово, либо для решения одних и тех же задач через определенные промежутки времени. Применение таких моделей для каких-либо измененных задач требует значительных затрат времени на их модификацию. Большое распространение получило также создание “гибридных” моделей, разрабатываемых для решения проблем, возникающих на стыке интересов разных секторов экономики. Такая модель “вырезает” из каждого сектора лишь некоторую часть, непосредственно связанную с рассматриваемой проблемой. В качестве примеров можно привести ряд задач на стыке сельского и водного хозяйства [8], промышленности и строительства [9], промышленности и охраны окружающей среды [10]. Возможность их повторного применения, по-видимому, также мала из-за их существенной привязанности к конкретным условиям. Вышесказанное предопределило появление иного подхода к моделированию отдельных секторов регионального хозяйства. Суть его заключается в том, чтобы, не пытаясь конкурировать со специальными задачами развития отдельных производств, а ограничиваясь рамками только рассматриваемого производства (без элементов “гибридного” подхода), создать наиболее общую задачу развитиям размещения отрасли. Одна из первых попыток построения модели такого рода для сельскохозяйственного сектора была предпринята в конце 1970-х годов в Международном институте прикладного системного анализа [11]. Эта модель позволяла: выбирать специализацию сельского хозяйства региона, одновременно анализировать проблемы животноводства и растениеводства, описывать возможную трансформацию земель, выявлять необходимость мелиорации, учитывать севообороты, кормовые рационы в животноводстве и т. д. Таким образом, она была достаточно общей, чтобы в рамках системы региональных моделей учитывать проблемы развития сельского хозяйства. Идейным ее аналогом применительно к промышленности является унифицированная модель развития и размещения промышленного производства [12]. Она позволяет: рассматривать одно- и многопродуктовые системы, применять целочисленное и непрерывное описание производства, учитывать в модели транспорт и потребление готовой продукции (с элементами взаимозаменяемости), описывать варианты развития производства (реконструкцию и новое строительство), т. е. любую проблему развития промышленного сектора региональной экономики. Уже в процессе работы над системой региональных моделей появилась необходимость в обобщенной модели регионального водоснабжения. И хотя специфика водных систем делает эту задачу достаточно сложной, все же при некоторых допущениях удалось создать модель, учитывающую все возможные источники водоснабжения: несколько водотоков, внутрирайонное перераспределение воды, строительство искусственных водохранилищ и каналов, сезонные колебания потребности в воде, контроль за качеством поставляемой воды и т. д. Ясно, что в описываемой системе метод согласования решений должен быть достаточно универсальным и быстрым для того, чтобы работать в “связке” с большеразмерными задачами отдельных секторов региональной экономики. Первая проверка метода согласования была проведена на экспериментальной системе моделей, разработанной для “условного” региона [13]. Информация, используемая в моделях, также условна, однако основана на реальных соотношениях, нормативах и прочих показателях, характерных для региональной экономики. Упрощенный вариант системы, применяемый для эксперимента, состоит из следующих блоков: сельское хозяйство, промышленность и водное хозяйство. Все задачи базируются на пространственном, а не точечном описании объекта. Регион делится на 4 подрайона с относительно однородными условиями [14]. Основными варьируемыми параметрами в системе являются величины общих для региона ресурсов: капитала, воды и труда. Схема связей в системе показана на рисунок 1 Рисунок 1. Схема связей в экспериментальной системе моделей: 1 – координационный центр, 2 – сельское хозяйство (линейная модель, 200x100), 3 – промышленность (линейно-целочисленная модель, 75x25), 4 – водное хозяйство (линейноцелочисленная модель, 100x50); а – капитальные вложения, b – трудовые ресурсы, с – водные ресурсы, d – прибыль, е – затраты Figure 1. Relationship diagram in the experimental model system: 1 – coordination center, 2 – agriculture (linear model, 200x100), 3 – industry (linear integer model, 75x25), 4 – water management (linear integer model, 100x50); а – capital investments, b – labor resources, с – water resources, d – profit, e – costs Не все связи в системе одинаково значимы. Расчеты показали, что недопотребление в промышленности в рассматриваемом случае постоянно и им можно пренебречь; можно не учитывать и трудозатраты на водоснабжение, так как они невелики и не оказывают влияния на остальные отрасли. Для проверки точности приближенного метода естественно сравнивать результаты с точным оптимумом системы. Для данного экспериментального примера он может быть получен как решение задачи, объединяющей все три блока с общими ограничениями и явным выражением горизонтальных связей. Матрица “обшей задачи” состоит из отраслевых задач с внесенными в них следующими изменениями: 1. локальные ограничения по труду и капиталу заменяются общими; 2. вводятся переменные связи между сельскохозяйственной и водной задачами; это – объемы водопотребления на сельскохозяйственные нужды в отдельных подрайонах в сезоны “пиковой” нагрузки (летний и весенний полив); 3. применяется общий критерий оптимальности – максимум дохода от производственной деятельности региона. Ниже описывается итерационный процесс согласования решений. I итерация. Работа алгоритма начинается с построения функций отклика каждого блока. Проводя серию расчетов по модели при изменении величин основных варьируемых параметров, получаем последовательность оптимальных решений задач. Модель сельского хозяйства Модель линейного программирования размером 200x100 описывает основные структурные характеристики отрасли: развитие растениеводства и животноводства; использование земель разного качества, формирование кормовой базы, условий севооборота. Рассматриваются различные специализации в животноводстве; по каждой из них предусмотрены две технологии: обычная и интенсивная, отличающаяся затратами труда, воды, капитальных вложений, а также и результатами их применения. В растениеводстве также две технологии – поливная и бесполивная. Затраты на выращивание продукции без полива выше, так как отсутствие воды компенсируется другими агротехническими мероприятиями. Расходы на развитие мелиорации учитываются в отрасли водоснабжения. Для получения функции отклика проведены серии расчетов при изменении параметров трудовых ресурсов (Т), объема капитальных вложений (К) и объема годового водопотребления (W). Отправная точка расчетов: Т=180 тыс. чел., К=90 млн р., W=0,5 млрд м3/г. Это – минимальные величины ресурсов, ниже которых нет допустимого решения задачи. Шаг изменения параметров был выбран эмпирически и составил примерно 10% первоначального значения. Далее расчеты проводились до момента насыщения, когда дальнейшее увеличение параметра не дает существенного изменения функционала. Характеристики изменения параметров показаны в таблице 1. Таблица 1. Характеристики изменения параметров Table 1. Characteristics of parameter changes Параметр | Parameter Интервал | Interval Шаг | Step Изменения | Changes Т, тыс. чел. T, thousand people 100–260 20 К, млн р. K, million rubles 90–140 10 W, млрд м3/г W, billion m3/ year 0,5–1,1 0,2 В указанных точках получены значения функционала задачи, которые и представляют собой функцию отклика блока “сельское хозяйство”. Эта функция нелинейна. По каждому виду ресурсов происходит “насыщение”, если два других ресурса фиксированы. Вид функции для W = 0,5 представлен на рисунке 2. Кроме функции отклика, расчеты дают возможность определить внутрирайонное распределение водных ресурсов для сельского хозяйства. Как показали расчеты, функция отклика водной задачи существенно зависит не только от общей нагрузки на регион, но и от того, как она распределена по водотоку. Водное хозяйство Модель частично целочисленная, размерности 100x50, учитывает все основные факторы и объекты водной системы региона: внутригодовую неравномерность стока, строительство каналов, водохранилищ, очистку воды от загрязнения. Регион поделен на четыре водохозяйственных участка. В нашем “условном” регионе основная нагрузка на водную систему связана с сельским хозяйством, поэтому варьируется параметр W, который принимает значения 0,5; 0,7; 0,9; 1,1. Однако, как указывалось, на изменение функционала водной задачи оказывает влияние не только общая величина водопотребле-ния, но и распределение нагрузки по водохозяйственным участкам. Например, потребление воды на четвертом участке связано с дополнительными затратами на строительство водовода; потребление в первом участке также менее выгодно, так как в верховье реки сток меньше, чем ниже по течению и т. д. Исследования показали, что приближенно варианты распределения нагрузки могут быть описаны как следующие стратегии: I – равномерное распределение нагрузки по участкам; II – равномерное распределение на первом – третьем участках, а на четвертом – лишь небольшое водопотребление; III – “блокируются” первый и четвертый участки, нагрузка распределяется на втором и третьем. Рисунок 2. График функции отклика блока “Сельское хозяйство”: F – целевая функция, млн р.; К – капитальные вложения, млн р.; Т – тыс. человек Figure 2. Graph of the response function of the “Agriculture” block: F – objective function, mln rub.; K – capital investments, mln rub.; T – thousand people Решение задачи с разными стратегиями и различным уровнем годового недопотребления дает картину изменения функционала – функцию отклика блока “водное хозяйство” (рисунок 3). Рисунок 3. График функции отклика блока “Водное хозяйство”: F – функционал, млн р.; W – водопотребление, млрд м3; I–III – стратегии Figure 3. Graph of the response function of the “Water Management” block: F – functional, million rubles; W – water consumption, billion m3; I–III – strategies Промышленность Блок промышленности включает описание трех видов условной продукции с различными типами производства. Один из них представлен непрерывной переменной и позволяет осуществлять прирост мощностей любой величины в пределах потребности, два других – целочисленные, причем по второму виду имеется дискретный набор мощностей, а по третьему – предусмотрен лишь один типовой объем. Рассмотрен выбор технологий (более или менее трудоемких и капиталоемких), а также выбор размещения предприятий по четырем районам. Варьировались параметры Т и К; по параметру W расчеты не проводились, так как анализ показал, что в этой постановке задачи варьирование водопотребления не оказывает влияния на решение задачи. Диапазон изменения трудозатрат – от 95 до 135 тыс. человек. Капитальные вложения изменялись от 700 до 750 млн р. Функция отклика носит существенно нелинейный характер; изменение функционала (приведенных затрат) происходит скачкообразно (таблица 2). На основе полученных функций отклика строится задача целочисленного программирования для согласования решений отдельных блоков. Ее матрица схематично представлена в таблице 3. Переменные принимающие значения нуль и единица, дают возможность выбрать вектор значений параметров К, Т и W, и соответствующее значение функции отклика f (K, T, W) при заданных общих ресурсах К, Т и W. Число уравнений координационной задачи – это число варьируемых ресурсов плюс число блоков в системе; количество переменных определяется суммой рассматриваемых вариантов для всех блоков. Таблица 2. Скачкообразное изменения функционала Table 2. Hopping functional changes К, млн р. К, mln rub. Т, тыс. чел. Т, thousand people 95 105 115 125 135 700 * * * 86 86 710 * * 87 83 83 720 * 88 83 83 83 730 * 84 83 83 83 740 85 84 83 83 83 750 85 84 83 83 83 – несовместное решение | incompatible solution Таблица 3. Матрица согласования решений отдельных блоков Table 3. Matrix of coordination of decisions of individual blocks Функционал f (K, T, W) (функции отклика блоков) | Functionality (block response functions) OQ W a о к D ° л> 8 s CD £ К К • S О Sc Хи X2 i Хз i Варианты решений задачи | Options for solving K T W Сельскохозяйственной | Agricultural Промышленности | Industry Водной | Water 1 1… 1 < 1 1 1… 1 < 1 1 1… 1 < 1 В нашей задаче для блока сельского хозяйства было 104 варианта, для промышленности – 10, для водного хозяйства – 12. Решение координационной задачи дает оптимальный вариант распределения ресурсов между блоками системы при данной точности описания функций отклика. Сравнение полученного решения с точным оптимумом системы (решением общей задачи, которая была описана выше) показывает, что первая итерация дает лишь грубое приближение к оптимуму: разница функционалов составляет примерно 10% (таблица 4). II итерация. Для продолжения итерационного процесса необходимо уменьшить область изменения параметров и шага по каждому из них. Правила построения новой “сетки” изменения параметров сводятся к следующему. 1. Исследование функции отклика проводится в окрестности точки, выбранной в качестве оптимума на предыдущей итерации. Например, для блока “сельское хозяйство” в качестве 2. Для области изменения выбирается интервал между соседними точками “сетки” изменения параметров на предыдущей итерации. В нашем примере из сетки изменения параметров выбрана область: Т = 100 - 200, K = 100-110-120; W = 0,5 -0,7 . 3. Выбор нового шага изменения параметров – эмпирический. Полученный интервал делится на отрезки более мелкие, чем на итерации I. отправной точки берется оптимальное решение на итерации I: TI = 180, KI = 110, WI = 0,5. В нашем примере: Т: 180–185–190–195– 200; К: 100–105–110–115–120; W: 0,5–0,55–0,6– 0,65–0,7. Построение функций откликов происходит так же, как на итерации I. В сельскохозяйственной задаче одновременно определяются и объемы потребления воды, которые служат основой для построения стратегий водопотреб-ления в водной задаче. Поскольку на первой итерации была выбрана вторая стратегия водопотребления, то именно она будет использоваться в дальнейшем. Исходя из полученных функций отклика строится новая координационная задача. Решение ее существенно отличается от оптимума, рассчитанного на итерации I (таблица 4). Это главный признак, указывающий на необходимость продолжения итеративного процесса. III итерация. Анализ оптимального решения показывает, что основные изменения произошли в блоке сельского хозяйства: выбран вариант K=110, Т=185, W=0,5, т. е. изменилось значение параметра T. Следовательно, на итерации III необходимо построить новую “сетку” по параметру Т. Интервал изменения – окрестность точки Т: 183–184–185–186–187. В остальных блоках функции отклика вычислялись аналогично предыдущей итерации. После этого была построена новая координационная задача и найдено оптимальное решение. Значение функционала на III итерации не изменилось. Таким образом, итеративный процесс нахождения приближенного решения можно закончить. В таблице 4 приводятся данные, позволяющие сравнить решения, получаемые на последовательных итерациях. Сопоставление функционалов приближенного и точного решений показывает, что погрешность составляет менее 0,4%. Таблица 4. Сводная итоговая таблица Table 4. Summary table Показатели | Indicators Координационная задача Coordination task Общая задача (точное решение) General task (exact solution) I II III Значение функционала F | Functional value F -64,05 -56,87 -56,87 -56,60 Ресурсы в том числе по блокам: Resources including by blocks Т 280 280 280 280 К 880 880 880 880 Сельское хозяйство | Agriculture Функционал F | Functional F 23,5 30,68 30,68 30,68 Ресурсы | Resources Т 180 185 185 185,01 К 110 110 110 110,01 Промышленность | Industry Функционал F | Functional F -85 -85 -85 -85 Ресурсы | Resources Т 95 95 95 94,99 К 740 745 747 739,90 Водное хозяйство | Water industry Функционал F | Functional F -2,55 -2,55 -2,55 -2,17 Ресурсы | Resources Т 0 0 0 0 К 9,3 9,3 9,3 7,3 Заключение Экспериментальные расчеты свидетельствуют о том, что использование изложенного метода обладает рядом преимуществ по сравнению с точными методами согласования. К ним можно отнести: ─ возможность работы с разнообразными, достаточно крупными задачами, описывающими реальные экономические объекты; ─ учет нескольких параметров, выступающих в качестве глобальных ресурсов в системе при нахождении согласованного решения; ─ относительную простоту алгоритма, использование уже отработанных стандартных процедур оптимизации отдельных блоков, стандартных пакетов оптимизации; ─проведение многовариантных расчетов, разработки различных сценариев развития региональной экономики.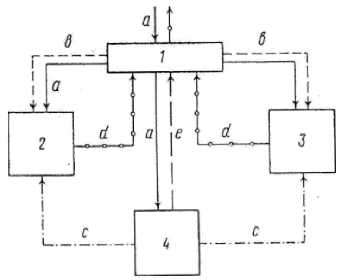
Список литературы Обоснование использования функций отклика при формализации задач экономического управления регионом
- Шелобаев С.И. Математические методы и модели. М.: ЮНИТИ, 2018. 217 с.
- Баканов М.И., Мельник М.В., Шеремет А.Д. Теория экономического анализа: 5е изд., перераб. и доп. М.: Финансы и статистика, 2017. 194 с.
- Васин А.А., Морозов В.В. Теория игр и модели математической экономики. М.: МАКС-Пресс, 2015. 207 с.
- Дубина И.Н. Математические основы эмпирических социально-экономических исследований. Барнаул: Изд-во Алтайского университета, 2016. 184 с.
- Таха X.Л. Введение в исследование операций. М.: Вильямс, 2015. 273 с.
- Хили Дж. Статистика: Социологические и маркетинговые исследования. СПб.: Питер, 2005. 193 с.
- Нестеров Ю.Е. Введение в выпуклую оптимизацию. М.: МЦНМО, 2016. 225 с.
- Лапшина М.Л., Лапшин Д.Д., Князев А.В., Писарева С.В. и др. Моделирование ситуации неплатежей на основе средств дифференциального исчисления в системе интеграции предприятий // МОИТ. 2019. Т. 7. № 3 URL: http://moit.vivt.ru
- Лукина О.О. Инновационная деятельность как сложная система функционирования и развития хозяйствующих субъектов // Экономика и предпринимательство. 2017. № 8 (2). С. 711-714.
- Измаилов А.Ф., Третьяков А.А. 2регулярные решения нелинейных задач. Теория и численные методы. М.: Лань, 2019. 218 с.
- Волошин Г.Я. Методы оптимизации в экономике. М.: Дело и Сервис, 2017. 184 с.
- Sine W.D., Mitsuhashi H., Kirsch D.A. Revisiting Burns and Stalker: Formal structure and new venture performance in emerging economic sectors // Academy of management journal. 2006. V. 49. № 1. P. 121-132.
- Kim K., Park J.H., Prescott J.E. The global integration of business functions: A study of multinational businesses in integrated global industries // Journal of international business studies. 2003. V. 34. № 4. P. 327-344.
- Davila A., Foster G., Li M. Reasons for management control systems adoption: Insights from product development systems choice by early-stage entrepreneurial companies // Accounting, Organizations and Society. 2009. V. 34. № 3-4. P. 322-347.


