Обоснование эмпирической формулы Пустовойта-Дьякова, определяющей оптимальный фенотип подсолнечника по урожайности
Автор: Григулецкий В.Г.
Рубрика: Селекция и семеноводство сельскохозяйственных растений
Статья в выпуске: 1 (185), 2021 года.
Бесплатный доступ
В статье используются результаты полевых опытов А.Б. Дьякова за 1960-1968 гг., выполненных во ВНИИМК под руководством академика В.С. Пустовойта. Особое внимание уделено результатам изучения влияния густоты стояния растений на урожайность подсолнечника и продолжительность роста растений. Для описания зависимости урожайности подсолнечника от площади питания растения ранее (академик Пустовойт В.С. и Дьяков А.Б., 1967 г.) предложено использовать эмпирическую формулу, учитывающую площадь питания ( х ), предельно возможный урожай растения ( А ), действие факторов роста ( с ) и параметр ( b ), определяющий часть площади питания растения подсолнечника, не оказывающую влияние непосредственно на урожай семян. Кривые урожайности подсолнечника, построенные по предложенной эмпирической формуле для 250 опытов, удовлетворяют условию 5%-ного уровня существенности. Применение эмпирической формулы позволило исследовать многие практические вопросы селекции и физиологии подсолнечника. Учитывая основные положения математической биофизики и математической теории борьбы за существование, установлено обыкновенное дифференциальное уравнение первого порядка для описания относительной скорости изменения урожая растения (уравнение П.Ф. Ферхюльста). На основе решения этого уравнения (с соответствующими начальными условиями) получена новая строгая аналитическая формула для определения урожая растения, учитывающая перечисленные выше факторы. В статье проведены расчеты, показывающие хорошее соответствие данных, получаемых по эмпирической формуле Пустовойта-Дьякова и по новой формуле: различие составляет менее 10 %. Эту формулу можно использовать при исследовании и решении разных вопросов физиологии растений (не только подсолнечника) и при оптимизации агротехнических мероприятий. Проведенный анализ позволил строго доказать и обосновать справедливость эмпирической формулы Пустовойта-Дьякова, определяющий оптимальный фенотип подсолнечника по урожайности.
Урожайность, подсолнечник, полевые опыты, площадь питания, эмпирическая формула, дифференциальное уравнение, общий интеграл, скорость роста, предельно возможный урожай
Короткий адрес: https://sciup.org/142229245
IDR: 142229245 | УДК: 633.854.78:582.683.2 | DOI: 10.25230/2412-608X-2021-1-185-3-9
Текст научной статьи Обоснование эмпирической формулы Пустовойта-Дьякова, определяющей оптимальный фенотип подсолнечника по урожайности
Введение. В 1960–1968 гг. под руководством академика В.С. Пустовойта на полях отдела селекции Всесоюзного научно-исследовательского института масличных культур (ВНИИМК) А.Б. Дьяков выполнил фундаментальные исследования физиологических особенностей высокомасличных сортов подсолнечника [1; 2].
Экспериментальная база ВНИИМК была расположена на третьей террасе реки Кубань. Почва – западно-предкавказ-ский выщелоченный чернозем, отличающийся тяжелым механическим составом, чрезвычайно большой мощностью гумусового горизонта (150–200 см) и невысоким содержанием гумуса в верхних слоях. Обеспеченность калием хорошая, азотом и фосфором – средняя.
В качестве объектов исследования служили сорта масличного подсолнечника селекции ВНИИМК и других учреждений. При подборе сортов стремились к тому, чтобы различия по изучаемым признакам были максимальными, а различия по прочим признакам, особенно тем, которые связаны с масличностью семян и урожаем, – минимальными. Изучаемые признаки в значительной степени зависят от длины вегетационного периода, поэтому сравнивались между собой только сорта, близкие по продолжительности вегетации.
В диссертации А.Б. Дьякова [1] впервые доказано экспериментально, что 4
урожай масла в подсолнечнике повышается не в результате увеличения площади листьев или продолжительности их работы, а за счет повышения средней интенсивности фотосинтеза. Кроме того, в этой работе А.Б. Дьякова [1] впервые доказано экспериментально очень сильное влияние густоты стояния растений на продолжительность жизни подсолнечника. Установлено, что при обычной густоте стояния растений подсолнечника сорта ВНИИМК 8931 (40 тыс. раст./га) к моменту полной спелости семян почти все листья отмирают, а при увеличенной площади питания (10 тыс. раст./га) часть средних и все верхние листья остаются зелеными даже после того, как полностью созревают семена. Увеличение площади питания явно повлияло на размеры и внешний вид корзинок и семян, повысилась интенсивность накопления масла и, особенно, не жировых веществ семян.
Анализ результатов полевых опытов за 1963–1968 гг. показал, что фактические данные по урожайности ( у ) подсолнечника не согласуются с результатами расчетов по известной эмпирической формуле Э.А. Митчерлинха:
y = л ( 1 - 10 - cx ) , (1)
где А – предельно возможный урожай;
с – коэффициент действия факторов роста;
х – площадь питания растения [2].
Вместо формулы (1) предложено использовать следующую зависимость:
y = a [ 1 - 10 - c ( x - b ) ] , (2)
где b – постоянный коэффициент (соотношение (2), стр. 72 [2]).
Специально отмечается «необходимость введения параметра «b», свиде-тельствущего о том, что часть площади питания растений подсолнечника не ска- зывается непосредственно на урожае семян» ([2], стр. 72).
По данным опыта 1966 г., величины А , с и b оказались равными:
А = 138; с = 1,3; b = 0,05
и можно записать формулу:
у = 138 [1 -10-1,3( х-0,05)]. (3)
На рисунке 1 показаны кривые урожайности подсолнечника, построенные по формуле (3) при 5%-ном уровне существенности при 250 опытах.
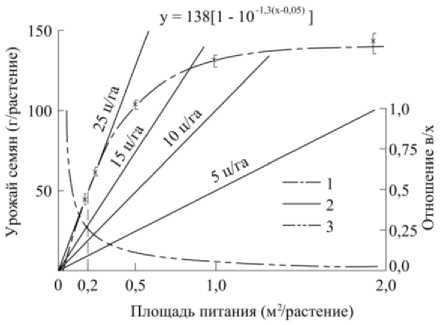
Рисунок 1 - Зависимость урожая семян от площади питания растений подсолнечника [2]:
1 - линия регрессии урожая семян (г/растение) на площадь питания;
2 - линии равного урожая семян (ц/га);
3 - доля «физиологически недействующей» на урожай площади питания (отношение в/х). ( Доверительные интервалы показаны на
5%-ном уровне существенности при п = 250) (Дьяков, 1969 г.)
Результаты расчетов по формуле (2) (и в частности формула (3) использовались в статьях [3; 4] и монографии [5]. При характеристике особенностей взаимоотношения растений в посеве ([5], стр. 35-37), специально отмечается, что «обеспеченность растений подсолнечника факторами внешней среды определяется не только почвенно-климатическими и погодными условиями, но в значительной мере взаимовлиянием их в посеве, конкуренцией между ними за свет, воду, усвояемые соединения азота, фосфора и другие факторы роста. Чем менее загущен посев, тем в более благоприятных условиях развивается каждое растение, тем полнее реализуется их потенциальная урожайность: больше закладывается цветков в корзинке, ниже пустозерность, крупнее семена. Однако представление о том, что максимальный урожай посева может быть достигнут только при наилучшем удовлетворении потребностей и полной реализации потенциальной продуктивности каждого растения, является ошибочным.
По мере уменьшения густоты стояния возрастает освещенность растений подсолнечника, но снижается продуктивность использования света посевом, а при улучшении условий азотного питания урожай семян на одно растение повышается, но в расчете на единицу количества азота уменьшается.
Чем больше влаги содержится в почве, тем выше урожай семянок и вегетативной массы, но тем менее продуктивно расходуется вода растениями подсолнечника. То же самое наблюдается и при изменении обеспеченности растений остальными факторами внешней среды, кроме температуры.
А для сельскохозяйственного производства несравненно более важной задачей является получение максимального урожая с каждого гектара пашни, чем реализация потенциальной урожайности каждого растения.
Поэтому высокоурожайным с производственной точки зрения может быть только такой посев, в котором каждое растение получает недостаточное количество факторов внешней среды и не имеет условий для реализации всех своих возможностей, однако с единицы площади при этом собирают наивысший урожай. Судя по снижению масличности семян, снабжение растений подсолнечника азотом улучшается при увеличении площади питания одного растения до 2 м2, а наи- высший урожай с единицы площади посева достигается при площади питания одного растения, равной 0,18–0,25 м2, когда вес семян с одного растения в среднем в 2,5–3 раза меньше максимально возможного. Следовательно, в оптимальном по густоте посеве каждое растение подсолнечника получает в 8–10 раз меньшую площадь питания, чем нужно для удовлетворения всех его потребностей.
При чрезмерном загущении урожай семян подсолнечника с гектара также снижается.
Установлено, что зависимость величины урожая семян на одно растение ( у ) от размера площади его питания ( х ) описывается уравнением (2), где параметр А определяет максимально возможный урожай на растение, параметр с определяет действие факторов роста, а параметр b равен части площади питания, соответствующей количеству факторов внешней среды, расходуемых на создание вегетативной массы растений и не влияющих непосредственно на урожай семян.
Специально отмечается, что по мере загущения посева усиливается конкуренция между растениями, вынуждая их все более продуктивно использовать факторы среды для образования урожая семян. Но одновременно пропорционально числу растений на гектаре увеличивается непродуктивное расходование факторов среды на образование вегетативной массы. Когда доля непродуктивно используемой площади питания составит более 25 % (отношение b > 0,25 ), дальнейшее x загущение посева подсолнечника приведет к снижению урожая семян с гектара. Например, чем гуще посев, тем большая часть запасов влаги расходуется до цветения.
Из вышеизложенного следует, что взаимное угнетение растений в результате конкуренции и недоразвитие части зало-жившихся элементов структуры урожая является обязательным условием высоко- продуктивных посевов подсолнечника. При равномерном размещении растений их взаимное угнетение начинается не сразу после появления всходов, а тем позже, чем реже посев. Для условий Краснодара показано, что в оптимальном по густоте посеве взаимное угнетение растений начинает отрицательно влиять на увеличение их сухого веса только с фазы бутонизации. Оказалось, что объясняется это конкуренцией между корневыми системами, а не между надземными органами» (рис. 2.
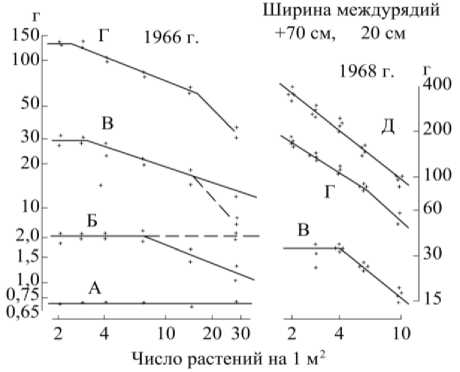
Рисунок 2 – Зависимость сухого веса надземных органов (г/растение) от густоты стояния растений подсолнечника.
Фазы: А – всходы; Б – 8 настоящих листьев; В – появление соцветия (бутонизация);
Г – цветение; Д – налив семян (Дьяков, 1969 г.)
Формула (3) использовалась при выборе оптимального фенотипа подсолнечника и изучении продукционных процессов в агроценозах с целью реализации полной потенциальной продуктивности [6].
А.Б. Дьяков отмечает, что многие агротехнические приемы влияют на формирование урожая подсолнечника посредством изменения конкурентных взаимосвязей между растениями.
Например, при внесении высоких доз удобрений значительно усиливается накопление биомассы посевами подсолнечника в фазе бутонизации. Однако ослабление конкуренции за элементы минерального питания приводит к усилению конкуренции за влагу, в результате чего урожай семянок может оказаться сниженным при высоком урожае общей биомассы ([6], стр. 52–53).
Обоснование эмпирической формулы (2).
Воспользуемся классической математической моделью внутривидовой конкуренции биологических популяций, предложенной П.Ф. Ферхюльст (Par P.-F. Verhulst) в 1838 г. [7; 8]. Применение и обобщение этой модели относительно к взаимодействию растительных сообществ дано в ранее опубликованных работах [9; 10].
Учитывая результаты полевых опытов [1; 2; 3; 4; 5; 6] и следуя А.Б. Дьякову, принимаем следующие обозначения: у – урожайность семян (г/раст.);
х – площадь питания растения (м2/раст.).
Как это принято в математической биофизике [8] и математической теории борьбы за существование [9; 10; 11], запишем основное дифференциальное уравнение для относительной скорости изменения урожая растения:
dy
4- = aУ-вУ , dx
P - постоянный коэффициент, учитывающий действие лимитирующих факторов на относительный рост урожая растения;
К – постоянный коэффициент, определяющий «емкость среды» и равный значению максимального урожая семян растения.
Коэффициенты a , P , r, K взаимосвязаны между собой: a = r и a = P К .
Отметим, что первый член уравнения (4) определяет относительную скорость роста продуктивности растения, пропорциональную урожайности, т. е. это – потенциальная скорость роста урожайности.
Второй член уравнения (4) отражает внутривидовую конкуренцию растений и он определяет относительную скорость торможения урожайности растения.
Коэффициенты a и P (как и параметры a , К) зависят от окружающей температуры, освещенности, субстратов питания растений и т. д.
Для решения дифференциального уравнения (6) принимаем «начальные» условия вида:
У(xo ) = Уо, (7)
или:
dy = (a-PУ )у, dx
х 0 , у 0 – постоянные, определяющие «начальную» площадь питания ( х 0 ) и «начальный» урожай ( у 0 ) растения.
или, окончательно:
dy I 1— = ry I 1 dx I
—
y
K
Решение уравнения (6), удовлетворяющие условиям (7) [11; 12] можно записать в виде:
a , P , r, K - постоянные коэффициенты.
Физический смысл постоянных коэффициентов a , P , r , K уравнений (4)-(6) заключается в следующем:
a - постоянный коэффициент, определяющий относительный рост урожая подсолнечника без учета лимитирующих факторов ( a = r );
У(x ) = —
1 +
K
( _^Уо
А
у K - Уо у
( „ A 4°y
V K - у о J
er ( x - x о )
.
exp[r (x - x0)]
Легко проверить, что при х = х 0 , имеем
У(хо ) = Уо.
Формулу (8) можно записать в виде:
y ( x ) = K
1 4 1
I к - y o J
exp [ r ( x - x 0 ) ]
Формулу Пустовойта-Дьякова (2) мож- но записать в виде:
y (x )= A 11-ry " ’ ioc(x-b)
В частном случае, учитывая, что In 10 * 2,303 и 10 ' е2,303 для опытных данных 1966 г., когда получены значения [2]:
х0 = 0,05; А = К = 138; r = с = 1,3, можно записать эмпирическую формулу
Пустовойта-Дьякова в виде:
y = 138 ^ 1 -
exp [ 2,994 ( x - 0,05 ) ]
и новую формулу в виде:
y = 138 ^ 1 -
1 + exp [ 2,994 ( x - 0,05 ) ]
Ниже в таблице приведены результаты расчетов по формулам (11) и (12).
Таблица
Результаты расчетов продуктивности растений подсолнечника в зависимости от площади питания по разным формулам
|
№№ п/п |
х (м2/раст.) |
Формула (11), г/раст. |
Формула (12), г/раст. |
|
1 |
0,5 |
102,1 |
109,5 |
|
2 |
0,6 |
111,4 |
115,7 |
|
3 |
0,7 |
118,3 |
120,8 |
|
4 |
0,8 |
123,4 |
124,8 |
|
5 |
0,9 |
127,2 |
127,9 |
|
6 |
1,0 |
130,0 |
130,4 |
|
7 |
1,1 |
132,0 |
131,4 |
|
8 |
1,2 |
133,6 |
133,7 |
|
9 |
1,3 |
134,7 |
134,8 |
|
10 |
1,5 |
136,2 |
136,2 |
|
11 |
2,0 |
137,6 |
137,6 |
Данные таблицы показывают хорошее соответствие результатов расчетов по эмпирической формуле Пустовойта-Дьякова (11), которая установлена по экспериментальным наблюдениям 250 опытов при 5%-ном уровне существенности и по новой формуле (12), которая определена как решение задачи Коши для классического уравнения П.Ф. Ферхюльста.
Выводы . 1. Обоснована и строго доказана справедливость эмпирической формулы Пустовойта-Дьякова, определяющая оптимальный фенотип подсолнечника по урожайности.
-
2. Проведены расчеты, показывающие хорошее соответствие данных, получаемых по эмпирической формуле Пусто-войта-Дьякова и новой формуле: различие составляет менее 10 %.
-
3. Полученную новую формулу можно использовать при исследовании и решении разных вопросов физиологии растений и оптимизации агротехнических мероприятий.
Список литературы Обоснование эмпирической формулы Пустовойта-Дьякова, определяющей оптимальный фенотип подсолнечника по урожайности
- Дьяков А.Б. Физиологические особенности высокомасличных сортов подсолнечника // Автореф. дис. ... канд. биол. наук. -Краснодар: Кубанский сельскохозяйственный институт, 1966. - 18 с.
- Дьяков А.Б. Характер зависимости урожая семян от площади питания растений подсолнечника // Бюл. НТИ по масличным культурам ВНИИМК. - 1969. - Март. -С. 71-75.
- Пустовойт В.С., Дьяков А.Б. Урожайность подсолнечника и пути ее повышения в процессе селекции // Селекция и семеноводство. - 1971. - № 1. - С. 25-30.
- Пустовойт В.С., Дьяков А.Б. О селекции подсолнечника на содержание белка в семенах // Вестник сельскохозяйственной науки. - 1972. - № 7. - С. 11-15.
- Подсолнечник: монография / Под общ. ред. акад. В.С. Пустовойта. - М.: Колос, 1975. - 591 с.
- Дьяков А.Б. Физиология подсолнечника. - Краснодар: ВНИИМК, 2004. - 76 с.
- Par P. -F. Verhulst. Notice sur la loi que la population suit dans son ac-croissement // Correspondance Mathema-tique et Physique. -Paris, Leipzig, 1838. - Vol. X. - P. 113-121.
- Ризниченко Г.Ю. Математические модели в биофизике и экологии. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 184 с.
- Григулецкий В.Г. Математическая модель взаимодействия растительных сообществ. Часть I // Московский экономический журнал. - 2018. - № 5: -[Электронный ресурс]. - Режим доступа: https://qje.su/ekonomicheskaya-teoriya/mos-kovskij -ekonomicheskij -zhurnal-5-2018-85.
- Григулецкий В.Г. Математическая модель взаимодействия растительных сообществ. Часть II // Московский экономический журнал, 2018, № 5: - [Электронный ресурс]. - Режим доступа: https://qje.su/ekonomicheskaya-teoriya/mos-kovskij -ekonomicheskij -zhurnal -5-2018-86.
- Вольтерра В. Математическая теория борьбы за существование. - Москва-Ижевск.: Институт компьютерных исследований, 2004. - 288 с.
- Григулецкий В.Г., Ященко З.В. Высшая математика для экономистов. - Краснодар: КубГАУ, 2001. - 632 с.


