Обоснование параметров компьютерной модели сельской электрической сети 0,4 кВ в MATLAB Simulink

Введение.

В настоящее время математическое, а на его основе компьютерное моделирование режимов работы электрических сетей является одним из наиболее достоверных инструментов их изучения. Наиболее популярной программой для изучения режимов работы электрических сетей является MATLAB Simulink. Программа используется для решения большого набора задач, связанных с электрическими сетями, электроэнергетикой. Так, в работе [1] разработана модель электрической сети для питания железнодорожных составов от кольцевой сети постоянного тока, запитанных от двух тяговых подстанций 110/3,3 кВ. В работе [2] произведено исследование аварийных режимов работы электрической сети 10 кВ и приведены осциллограммы двухфазного и трехфазного коротких замыканий, а также однофазного замыкания на землю. Общим для вышеуказанных работ является отсутствие обоснования параметров моделей, что не позволяет сделать вывод о точности и достоверности полученных результатов моделирования, так как авторами используются стандартные значения блоков моделирования, которые заданы по умолчанию в программном комплексе. Такой подход может давать значительные погрешности при отличии технических характеристик исследуемых элементов электрической сети и предзаданных в программном комплексе.

Значительное количество работ, например, [3-6], в которых применена программа Matlab Simulink, связано с моделированием работы фотоэлектрических установок (ФЭУ) и выдачи ими мощности в сеть. Это позволяет получать вольтамперные характеристики солнечных панелей, исследовать графики выдачи мощности в зависимости от солнечной инсоляции, анализировать температуру солнечных панелей за время эксплуатации, исследовать загрузку трансформатора при работе сетевой солнечной электростанции с сетями среднего класса напряжения и выявлять экономическую эффективность применения ФЭУ.

Цель работы заключается в обосновании параметров элементов компьютерной модели сельской электрической сети 0,4 кВ, выполняемой в прикладной программе MATLAB SIMULINK.

Материалы и методы исследования.

На рисунке 1 представлен общий вид разработанной компьютерной модели электрической сети 0,4 кВ в программе MATLAB SIMULINK.

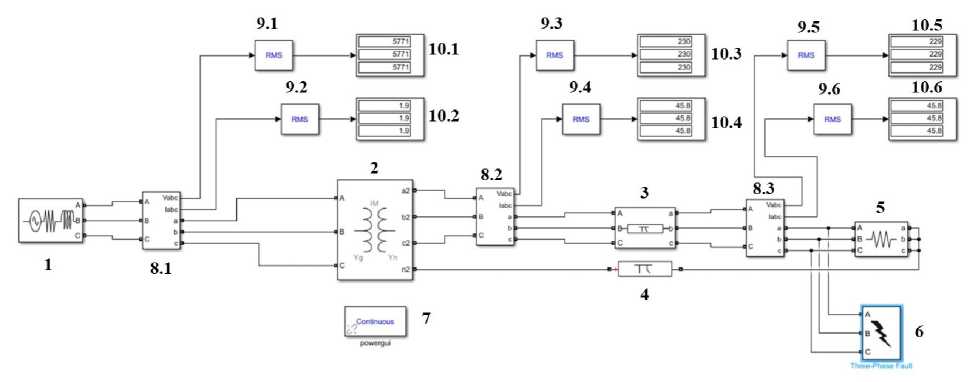
Рисунок 1 – Общий вид компьютерной модели сельской электрической сети 0,4 кВ: 1 – трехфазный источник с номинальным напряжением 10 кВ; 2 – двухобмоточный силовой трансформатор 10/0,4 кВ; 3 – модель фазных проводов линии электропередачи 0,4 кВ; 4 – модель нейтрального провода линии электропередачи; 5 – модель нагрузки 0,4 кВ; 6 – блок моделирования коротких замыканий; 7 – блок PowerGui; 8.1, 8.2, 8.3 – трехфазные блоки измерения токов и напряжений; 9.1, 9.2, 9.3, 9.4, 9.5, 9.6 – блоки вычисления среднеквадратичного значения; 10.1, 10.2, 10.3, 10.4, 10.5, 10.6 – дисплеи

При обосновании параметров элементов компьютерной модели сельской электрической сети 0,4 кВ частично использовались положения источников [7, 8].

Результаты и обсуждение.

Энергосистема 1 моделируется с помощью стандартного блока «Three-Phase Source» библиотеки Three-Phase Electrical [9]. Блок характеризуется следующими параметрами. Первым параметром является конфигурация источника, т.е. связь трех внутренних источников напряжения, среди которых можно выбрать схему соединения звезда (Y) и звезда с нейтральным проводом (Yn). В нашем случае была выбрана схема соединения в звезду (Y), так как она является характерной для электрических сетей среднего напряжения 6-35 кВ с изолированной нейтралью. Для следующего параметра междуфазного напряжения источника принимаем значение 10 кВ, а параметр начального значения угла напряжения фазы А принимаем равным 0 градусов, при этом параметр частоты, значение которой равно 60 Гц, меняем на стандартную для электрических сетей РФ – 50 Гц.

Следующий параметр задает сопротивление источника питания. Его численное значение определим согласно ГОСТ 28249-93 «Короткие замыкания в электроустановках.

Методы расчета в электроустановках переменного тока напряжением до 1 кВ» по формуле

(1):

Хс —

^U ср . НН ²

^ кз

^U ср . НН ²

V3-I к . ВН "U ср . ВН

(Ом),

где – U ср.НН среднее номинальное напряжение сети, подключенной к обмотке низшего напряжения трансформатора, 400 В;

U ср.ВН - среднее номинальное напряжение сети, к которой подключена обмотка высшего напряжения трансформатора, 10000 В;

I к.ВН - действующее значение периодической составляющей тока при трехфазном КЗ у выводов обмотки высшего напряжения трансформатора, кА. В качестве данного значения примем 1 кА, так как данные токи характерны для электрических сетей 6-10 кВ среднего класса напряжения, питающих сельских потребителей [10];

S k - условная мощность короткого замыкания у выводов обмотки высшего напряжения трансформатора, МВА.

Таким образом, сопротивление системы составляет:

Х с = _R иср™, ²   = 0,009 (Ом).                        (1)

Vd4 к . вн -U ср . вн

Следующим параметром необходимо задать индуктивность системы. Она рассчитывается по формуле (2) [7]:

^Lc = ^ ^                    (2)

где f – номинальная частота источника питания, 50 Гц;

π – число Пи, 3,14;

R c – активное сопротивление энергосистемы, Ом;

K – отношение индуктивного сопротивления энергосистемы к ее активному сопротивлению, о.е., которое рассчитывается по формуле (3) [7]:

К =   = ^к (о.е.),                                   (3)

R_c ln (К уд -1) ^{v л                                           v 7}

где K уд – ударный коэффициент, значение которого для распределительных электрических сетей 0,4 кВ принимаем равным 1,369 о.е. [11].

С использованием указанных положений определим значение индуктивности системы по формуле (2):

L = ^K_:^Rc = ₃.10 -5 (Гн).

^С 2lff

При этом индуктивность системы также можно выразить из формулы (4)

теоретических основ электротехники с учетом значения сопротивления энергосистемы, полученного по формуле (1) [12]:

X_L = 2л • f • L (Ом) (4)

В данном случае при принятии значения X L равным X c , расчеты позволяют выявить, что значение L составит 2,86∙10^-5 Гн. Таким образом, разность результатов составляет 4,6%. Для компьютерной модели будет использовать значение, полученное по формуле (2).

Еще одним параметром источника питания является базисное напряжение, предзаданное в программе значение которого составляет 25000 В. Оно используется для моделирования коротких замыканий. В разрабатываемой модели сельской электрической сети 0,4 кВ будем использовать значение 10000 В. Последним параметром трехфазного источника питания (энергосистемы) является тип источника. Для модели будет использоваться тип swing, который обеспечивает выработку активной и реактивной составляющей мощности, что не позволяют сделать другие типы источников.

Двухобмоточный трансформатор 2 моделируется с помощью блока «Three-Phase Transformer Inductance Matrix Type (Two Windings)» библиотеки Three-Phase Electrical [13]. Изначально необходимо задать следующие параметры. В качестве конструкции был выбран бронестержневой тип трансформатора с 5 стержнями, при этом для схем соединения обмоток со стороны высшего и низшего напряжения была задана звезда/звезда с нейтральным проводом (Y/Yn).

На следующем этапе необходимо задать параметры трансформатора. В качестве номинальной частоты элемента задаем значение 50 Гц, а номинальную мощность принимаем равной 250 кВА. В целом, трансформаторы мощностью 250 кВА широко распространены и их количество в электросетевой организации филиале ПАО «Россети Центр»-«Орелэнерго» составляет 802 единицы от общего количества электроустановок 6206, т.е. 13% [14]. Использование данной номинальной мощности трансформатора также позволит сопоставить результаты моделирования с другой математической моделью [15], расчетными методами и данными практической эксплуатации сельской электрической сети 0,4 кВ [16]. Для номинальных значений междуфазных напряжений сторон высшего и низшего напряжения задаем значения 10000 В и 400 В, соответственно.

Определим сопротивление трансформатора, приведенное ко вторичной обмотке по формуле (5) [7]:

2 т нн = —— = 0,64 (Ом),                       (5)

S Т.nom – номинальная мощность силового трансформатора, 250 кВА.

На следующем этапе необходимо задать активное сопротивление первичной и вторичной обмоток в относительных единицах. Оно определяется по формуле (6) [7]:

R 1 е = R ^ . е = ^е- =      (о.е.),                           (6)

2       2 2т .нн где RT – активное сопротивление трансформатора. Ом.

Активное сопротивление трансформатора рассчитывается по формуле (7) [7]:

R_t = ж.-и5™ = 0,₀095 (Ом),                    (7)

St . пот где ∆PКЗ – потери короткого замыкания, 3700 Вт, согласно [17];

U НН.nom – номинальное напряжение низшей обмотки трансформатора, 400 В;

S Т.nom – номинальная мощность силового трансформатора, 250 кВА.

В дальнейших расчетах потребуется полное сопротивление трансформатора, которое рассчитывается по формуле (8) [7]:

2_т = и кз% , и ннлголп. = 0,0288 (Ом),                      (8)

Таким образом, сопротивления первичной и вторичной обмоток в относительных единицах, согласно формулы (6):

R 1 - е - = R ⁰ - е = - ти_ = 0,0074 (о.е.).

² *^ т . нн

Также необходимо задать следующие паспортные параметры. Это ток холостого хода в процентах от номинального IXX% и потери холостого хода ∆Pxx. Принимаем данные значения равными 1,7% и 560 Вт, соответственно [17].

Следующим параметром, который необходимо определить, является индуктивное сопротивление трансформатора в относительных единицах, которое определяется по

формуле (9) [7]:

Х ое = ^г т -к т = 0,0425 (о.е.).

ZT. нн

Особенностью модели трансформатора в программной среде Simulink является то, что в ней необходимо задать параметры нулевой последовательности трансформатора для расчета несимметричных режимов работы. Первым из них является ток холостого хода нулевой последовательности I 0xx% в процентах от номинального. Изначально определим численное значение тока холостого хода нулевой последовательности I 0xx по формуле (10) [7]:

= и   ^т ф ) = ₉₀₆ (A),

Uлл        f                       X / '

JrM где X0 – реактивное сопротивление трансформатора нулевой последовательности, значение которого для ТМ-250-10/0,4 кВ Y/Yн составляет 0,235 Ом;

R 0 – активное сопротивление трансформатора нулевой последовательности, значение которого для ТМ-250-10/0,4 кВ Y/Y н составляет 0,097 Ом;

U нн.nom(ф) – номинальное фазное напряжение низшей обмотки трансформатора, 230 В.

При этом номинальный ток низшей обмотки силового трансформатора определим по формуле (11) [12]:

1нн.пот

S _т     _ 250^10 3

Va^u нн .пот ^_ Va^400

361 (А),

где S T – номинальная мощность силового трансформатора, 250 кВА;

U нн.nom – номинальное напряжение низшей обмотки трансформатора, 400 В.

Исходя из этого, ток холостого хода нулевой последовательности I 0хх% определим по формуле (12) [7]:

1 охх% = "Г^ " 100 = 251 (%).                     (12)

1 нн .п.от

Следует отметить, что значением по умолчанию является 100%, что позволяет сделать вывод об адекватности полученного численного значения, ввиду совпадения порядков расчетного и исходного значений.

Следующим параметром, который необходимо определить являются потери холостого хода нулевой последовательности, Р₀, обусловленные протеканием тока намагничивания нулевой последовательности. Они определяются по формуле (13) [7]:

Ро = Io2-Ro = 79211 (Вт) (13)

Последним параметром трансформатора, который необходимо задать является реактивное сопротивление нулевой последовательности в относительных единицах. Оно рассчитывается по формуле (14) [7]:

Х Ое' = = 0,37 (о.е.). (14) ^z T. нн

По умолчанию прикладная программа устанавливает это значение равным 0,03 о.е. Задание параметров модели трансформатора на этом завершено.

Фазные провода линии электропередачи 0,4 кВ 3 моделируются с помощью блока «Three-Phase PI Section Line», а нейтральный 4 моделируется с помощью блока «PI Section Line» библиотеки Three-Phase Electrical [18-19]. В качестве параметров в обоих блоках изначально необходимо задать частоту – 50 Гц. Далее для обоснования параметров провода примем, что сельская электрическая сеть 0,4 кВ выполнена проводом А-35 в связи с тем, что среди голых неизолированных проводов он является наиболее распространенным в сельских

электрических сетях 0,4 кВ по сравнению с другими марками и сечениями проводников; в отдельных линиях его протяженность может достигать до 50% от суммарной протяженности линии [20]. Следует отметить, что параметры провода задаются следующими характеристиками: активным сопротивлением прямой и нулевой последовательности (Ом/км), индуктивностью прямой и нулевой последовательности (Гн/км), емкостью прямой и нулевой последовательности (Ф/км).

Согласно [21] провод А-35 имеет следующие технические характеристики: активное сопротивление прямой последовательности (r 1уд ) – 0,868 Ом/км; активное сопротивление нулевой последовательности (r 0уд ) – 3,472 Ом/км; реактивное сопротивление прямой последовательности (x 1уд ) – 0,301 Ом/км; реактивное сопротивление нулевой последовательности (x 0уд ) – 1,204 Ом/км.

Индуктивность прямой последовательности рассчитывается по формуле (15) [7]:

L i уд = ^[ 4 + ^] • ¹⁰³ = ⁹⁹ • ^10-5 (Гн/км),              (15)

где μ 0 =4π∙10^-7 Гн/м – относительная магнитная проницаемость вакуума;

μ – относительная магнитная проницаемость материала проводника, которая для меди и алюминия составляем 1 Гн/м;

D ср – среднегеометрическое расстояние между фазными проводниками, которое вычисляется по формуле (16), или принимается равным 40 см по данным учебных пособий таких ученых, как И.А. Бузко, Т.Б. Лещинская, Олин Д.М., Попов Н.М.

R – радиус провода, который для провода А-35 составляет 0,375 см.

Dср = V/Dab • Dac • DBC (см).(16)

где D AB , D AC , D BC – расстояния между фазными проводами, см.

Индуктивность нулевой последовательности рассчитывается по формуле (17) [7]:

Loуд = ^[f + ln^^] • 103 = 109 • 10-5 (Гн/км),(17)

где D срN – среднегеометрическое расстояние между фазными проводниками и нулевым прводником, которое вычисляется по формуле (18), см:

Dсрn = VDan • Dbn • DcN = 68 (см).(18)

В свою очередь, расстояния D AN , D BN были рассчитаны как гипотенузы прямоугольного треугольника исходя из типового проекта трехфазной воздушной линии электропередачи 0,4 кВ с 4-мя неизолированными проводами «Унифицированные деревянные опоры ВЛ 0,4 и 6-10 кВ для особогололедных районов и районов с повышенными скоростями ветра. Выпуск I. Деревянные опоры ВЛ 0,4 кВ. Серия 3.407-118. Утверждены и введены в действие Минэнерго СССР с 1 июля 1976 г. Решение №102 от 13 мая 1976 г.» (рисунок 2).

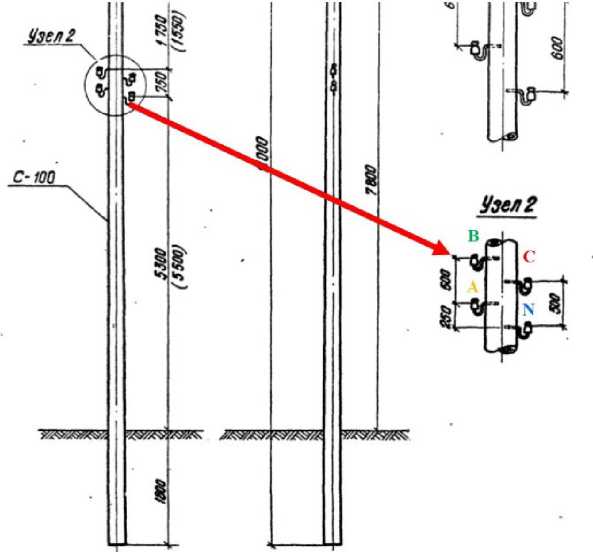
Рисунок 2 – Схема расположения проводов на промежуточной опоре воздушной линии электропередачи 0,4 кВ с 4-мя голыми проводами

Емкость линии прямой и нулевой последовательности линии электропередачи 0,4 кВ рассчитывается по формулам (19) и (20) [7]:

С1уд = “А^ = 12 • 10-9 (Ф/км);                  (19)

18-ln-^

С о уд =--- А = 10 • 10^-9 (Ф/км).                  (20)

18-ln

Последним параметром воздушной линии электропередачи 0,4 кВ является протяженность в километрах (L), которая в разрабатываемой модели будет варьироваться в разных пределах в зависимости от исследуемых режимов работы электрической сети.

Нагрузка (5 – рисунок 1) моделируется блоком Three-Phase Series RLC Branch [22], параметрами которого являются сопротивление в Омах, индуктивность в Генри, емкость в Фарадах.

Повреждения в разрабатываемой модели сельской электрической сети 0,4 кВ моделируются с использованием блока Three-Phase Fault (6 – рисунок 1) [23]. Блок позволяет моделировать разные виды повреждений путем выбора поврежденных фаз и земли (отмечать повреждения между элементами: фазой А, фазой В, фазой С и землей). Первым его параметром является время коммутации, позволяющее выбрать интервалы аварийного режимы за время моделирования. Это позволяет как получить осцилограммы нормального рабочего режима, переходящего в аварийный, так и исследовать установившийся аварийный режим работы электрической сети. Следующим параметром блока является сопротивление в точке повреждения, которое с учетом отечественного опыта расчета токов короткого замыкания можно назвать сопротивлением дуги, оно задается в Омах. Также в блоке задается сопротивление земли в Омах, необходимое для моделирования несимметричных аварийных режимов. Блок также позволяет задавать параметры сопротивления и емкости при обрыве провода на землю в электрической сети среднего класса напряжения с изолированной нейтралью. При этом данные параметры в разрабатываемой модели использоваться не будут.

Блок powergui (7 – рисунок 1) является системным и предназначен для отображения графического интерфейса пользователя, без него моделирование запустить невозможно [24].

Для измерения используются блоки Three-Phase V-I Measurement 8.1, 8.2, 8.3. Блоки позволяют измерять значения токов и напряжений в разрабатываемой модели сельской электрической сети 0,4 кВ [25].

Вычисление действующих значений токов и напряжений осуществляется с помощью блока «среднеквадратичное» 9.1-9.6, который определяет среднеквадратичное значение электрического параметра за период моделирования [26]. Единственным параметром блока, который необходимо задать, является частота электрической сети 0,4 кВ, равная 50 Гц для разрабатываемой модели.

Для отображения результатов моделирования используются блоки «дисплей» 10.110.6, который отображает значения электрических параметров, характерных для заданного режима работы сельской электрической сети 0,4 кВ [27]. Единственным параметром блока является формат отображения данных, который в используемой модели был задан в формате короткого, то есть в формате округления измеренного значения до тысячных.

В разрабатываемой модели сельской электрической сети 0,4 кВ также можно использовать и другие блоки для моделирования работы коммутационных аппаратов, возобновляемых источников энергии, параллельной работы нескольких трансформаторов, работы электрических машин как при их питании от трансформатора, так и параллельно с сетью. Они будут описаны в дальнейшем при исследовании отдельных режимов работы сельской электрической сети 0,4 кВ.

Заключение.

Обзор литературы выявил актуальность компьютерного моделирования электрических сетей в прикладной программе Matlab Simulink. В работе произведена разработка и обоснование параметров математической модели сельской электрической сети 0,4 кВ в Matlab Simulink. Разработанная модель позволит провести комплексное исследование режимов работы сельских электрических сетей 0,4 кВ, в том числе при использовании в них фотоэлектрических установок, средств секционирования.

https://docs.exponenta.ru/physmod/ sps/powersys/ref/threephaseseriesrlcbranch.html?ysclid=lmyli12dy0762208114          (accessed