Обоснование применения цилиндрического кейджа после вентральной декомпрессии при дегенеративных стенозах поясничного отдела позвоночника

Ââåäåíèå. В течение 10 лет в вентральной декомпрессии успешно используются цилиндрические титановые кейджы при дегенеративных стенозах поясничного отдела позвоночника, и отсутствие обоснования к его использованию, подвело нас к проведению математического моделирования с использованием методов конечных элементов. За период с 2004 по 2011 год нами было проопери- ровано 92 больных с дегенеративным стенозом поясничного отдела позвоночника и 52 больных - с «синдромом неудачно оперированного позвоночника». Оперативное вмешательство выполняли по методу Доценко-Загороднего с использованием цилиндрических имплантатов. Подробно данная методика описана в результатах работы Доценко В.В. с соавторами [1].

Целью данной работы является обоснование применения цилиндрического кейджа при вентральной декомпрессии с использованием конечно-элементного моделирования напряженно-деформированного состояния (НДС) изучаемой биомеханической системы (БМС). При исследовании элементов биомеханических систем приходим к задаче анализа напряженно-деформированного состояния пространственных конструкций, состоящих (с точки зрения механики деформированного твердого тела) из областей, занимаемых массивными телами, оболочками, нитевидными телами и т. д. К первым относятся тела опор (титановый кейдж, трабекулярная костная ткань). К оболочечным можно отнести боковую поверхность опоры, нижнюю и верхнюю замыкательные пластины. Нитевидные элементы могут использоваться при моделировании связок, мышц и т.д. [2].

Элементы биомеханических систем имеют сложную геометрическую форму и сложные законы нагружения, в связи с чем для определения их НДС необходимо привлекать численные методы. В частности, наиболее развитым в настоящее время для решения задач такого класса является метод конечных элементов [6], который и предложен для анализа НДС исследуемых элементов БМС.

МКЭ является мощным современным средством приближенного решения разнообразных задач математической физики, ориентированным на эффективное использование компьютеров. В задачах теории упругости он позволяет распространить принципы расчета систем на случай непрерывных тел и сложных конструкций. Для него характерны: широкий диапазон применимости, инвариантность по отношению к конструкции и механическим характеристикам материалов, простота учета взаимодействия конструкции с внешней средой.

Все программные продукты, реализующие МКЭ, используют его как метод, заложенный в программу SOLVER („решатель”), являющуюся основной составной частью продукта. Можно выделить программные продукты, являющиеся своего рода мировыми стандартами в рассматриваемой области: MSC/ NASTRAN, ANSYS, COSMOS/M, ABAQUS.

Однако при всех возможностях МКЭ, он является приближенным сеточным методом.

Точность результата МКЭ зависит от многих факторов: адекватности биомеханической модели условиям работы реальной конструкции, выбранного типа конечного элемента, формы и количества КЭ, на которые разбита модель. Поэтому знание теоретических допущений, принятых при моделировании конкретной задачи биомеханики, а также характеристик конечных элементов, предлагаемых в программных комплексах, необходимо для получения достоверного результата.

В современной трактовке МКЭ является приближенным вариационным методом. Суть метода заключается в дискретизации системы путем разбиения на конечные элементы, характеризуемые узлами, формой и числом степеней свободы. При этом осуществляется переход от системы с бесконечным числом степеней свободы к системе с конечным их числом. Все задаваемые нагрузки, геометрические и физические характеристики, начальная деформация при этом подходе сводятся к узлам [5].

С учетом многообразия типов конструктивных частей исследуемой биомеханической системы при использовании метода конечных элементов приходим к решению глобальной системы разрешающих уравнений МКЭ. При их формировании исходим из следующих гипотез:

• 1.    В первом приближении материал костных тканей, диска, связок и т.д. моделируется изотропным (или ортотропным) однородным материалом с известными физико-механическими характеристиками.

• 2.    Рассматриваются малые деформации и малые перемещения исследуемых объектов, в силу чего справедлив закон Гука для описания поведения материала.

• 3.    Контактное взаимодействие элементов исследуемой системы при соблюдении условий положительного давления в сопряжении элементов исследуемой биомеханической системы моделируется двусторонней связью сопряженных поверхностей.

Весь цикл исследований элементов биомеханической системы можно и необходимо разбить на отдельные этапы. При этом для определения напряженно-деформированного состояния элементов биомеханических систем, образуемых сегментами позвоночника с цилиндрическим кейджем, с целью до- стоверного моделирования НДС необходимо учитывать: сложность геометрической формы элементов БМС, которая представляет собой пространственную конструкцию, состоящую из разнородных по своей природе элементов; сложность объекта исследований как биомеханической системы взаимодействующих и взаимосоприкасающихся элементов; многообразие режимов эксплуатации и условий нагружения; сложные и резко отличающиеся физико-механические свойства элементов БМС [3].

Все перечисленные факторы в совокупности приводят к формулировке исходной задачи как пространственной задачи для БМС сложной структуры при воздействии на нее в общем случае набора пространственных сил. В связи с этим необходимо решить следующие задачи: сформулировать задачу определения НДС сегментов позвоночника и ци-

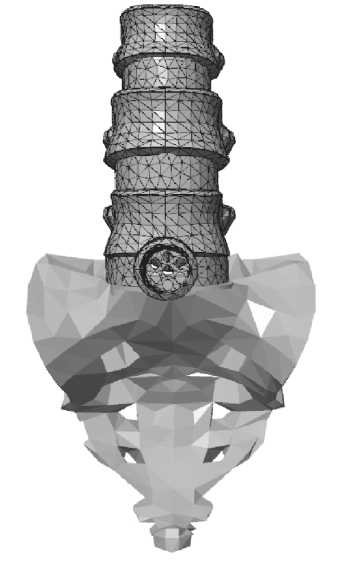
Рис. 1.

Таблица 1

Свойства материалов биомеханической системы

Название материала Модуль упругости, МПа Коэффициент Пуассона Трабекулярная ткань 67 0,2 Кортикальная ткань 3500 0,3 Фиброзное кольцо 100 0,3 Nucleus Pulposus 1 0,45 Титан 1,02е+5 0,3 линдрического кейджа как составных элементов биомеханической системы; провести дискретизацию задачи; разработать общую схему решения задачи определения напряженно-деформированного состояния элементов биомеханической системы; разработать дискретную модель исследуемой БМС; провести расчет НДС элементов биомеханической системы при варьировании основных параметров, сделать анализ результатов и выработать конкретные рекомендации, в данном случае - по обеспечению стабильности крепления и снижению травматичности при использовании цилиндрических кейджей. Рассмотрим этапы решения задачи.

• 1.    Расчетная схема биомеханической системы. В качестве базовой расчетной схемы рассмотрим систему, представленную на рис. 1.

• 2.    Конечно-элементная модель исследуемой биомеханической системы создается на основе геометрической модели сегмента позвоночника L3-S1, созданной в CAD-системе SolidWorks. Сама конечно-элементная разбивка осуществлена в системе MSC/NASTRAN.

На сегмент позвоночника из одного элемента цилиндрического кейджа действует тестовая система силовых факторов: вертикальное усилие и изгибающий момент в сагиттальной плоскости. Данная система сил соответствует системе сил, прикладываемых при расчетно-экспериментальном исследовании НДС элементов биомеханических систем в работах [4]. Свойства материалов представлены в табл. 1. Геометрические параметры элементов исследуемой системы приведены на рис. 1. Все фигурирующие на рис. 1 параметры сегмента L5-S1 поясничного отдела позвоночни- ка являются заданными в процессе каждого исследования.

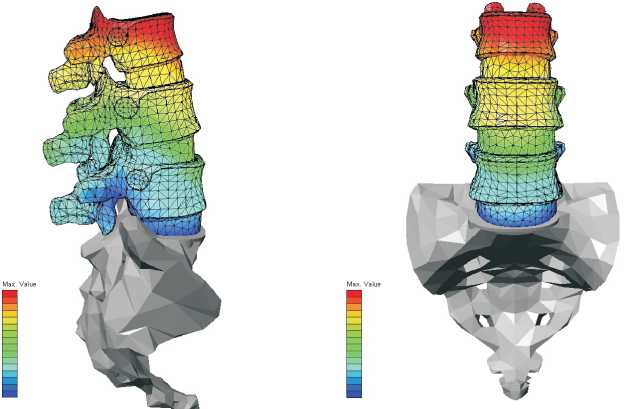
Рис 2. Расчет модели позвоночника в нормальных условиях

Расчеты показывают, что максимальное перемещение возникает в верхнем позвонке, минимальное перемещение – в нижнем позвонке.

Из расчетов видно, что несмотря на то, что нагрузка на позвоночник дается такая же как и в случае с позвоночником без импланта, самое большое перемещение возникает в ниж-

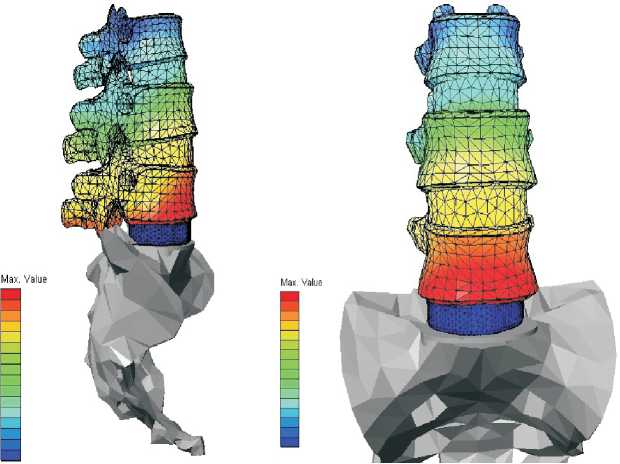
Рис. 3. Расчет модели позвоночника с расклинивающим межтеловым имплантом (сравнение).

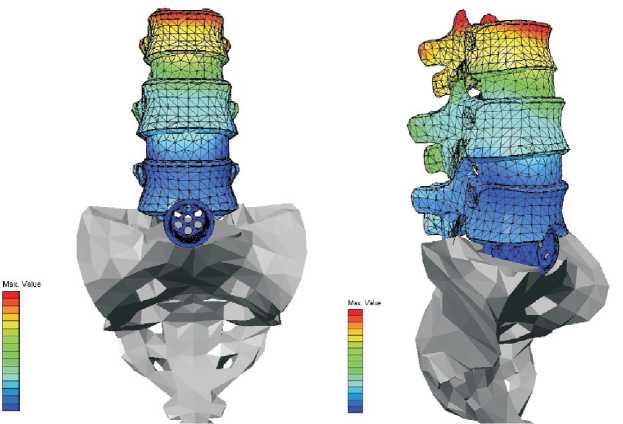
Рис. 4. Расчет модели позвоночника с одним кейджем

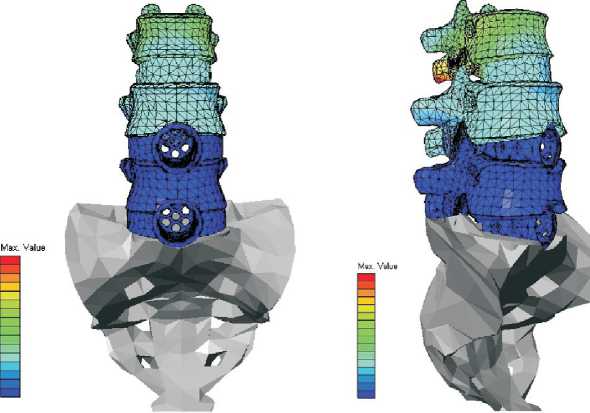
Рис. 5. Расчет модели позвоночника с двумя кейджами нем позвонке. Это происходит из-за вбивания импланта, т.е. межтелового расклинивающего корпородеза, при этом позвоночник, находящийся над имплантом перемещается вверх (рис. 3). Необходимо учитывать, что на позвоночник сверху давит сила и снизу (от импланта) происходит сжатие (перегрузка) межпозвоночных дисков, что приводит к дегенерации вышележащих дисков.

Из расчета видно, что позвоночник с кейджем испытывает практически такие же перемещения (равномерные), что и позвоночник без имплантата (рис. 4). Значения отличаются из-за того, что вместо нижнего диска вворачивается кейдж, который не сжимается и не перемещается, в отличие от естественного диска. Данный метод более предпочтителен, поскольку, в отличие от метода с имплантатом, на позвонки действует только нагрузка сверху (как и в здоровом позвоночнике), что не ведет к деградации вышестоящих дисков.

Такой же эффект мы можем видеть при использовании цилиндрических титановых кейджей при двухуровневом поражении (рис. 5).

В наших наблюдениях после проведенной операции вентральной декомпрессии с использованием цилиндрических титановых кейджей в течение 10 лет, на основании отдаленных результатов, а также рентгенологических, КТ и МРТ данных, мы пришли к выводу, что за счет адекватной декомпрессии путем краевой резекции прилегающих тел позвонков с созданием резервного пространства для нервных корешков, использование данных имплантов не приводит к ожидаемому восстановлению высоты межтелового пространства. При изучении отдаленных результатов с использованием цилиндрических титановых имплантов при схожих патологиях было установлено, что развитие проблем на смежных уровнях ПДС уменьшается в разы. Это объясняет тот факт, что мы отмечали единичные случаи повторного обращения больных с этой проблемой. Как объясняются такие результаты?

Была выдвинута гипотеза, которая нашла отражение в математическом обосновании к применению цилиндрического титанового имплантата при вентральном доступе к поясничному отделу позвоночника. Мы считаем, что сагиттальный баланс – это изменяе- мая величина в течении жизни, которая зависит от образа жизни человека, его веса, состояния мышечной структуры и естественного процесса старения.

В наших наблюдениях мы можем хорошо видеть как изменяется сагиттальный баланс в течение жизни, но не факт, что изменения сагиттального баланса в процессе жизнедеятельности и старения человека приведут к дегенеративному стенозу позвоночного канала. Вместе с тем, активное вмешательство в сагиттальный баланс путем восстановления высоты межтелового пространства приведет к его дисбалансу, неоправданной и чрезмерной его нагрузке в смежных сегментах, которые не заставят себя долго ждать и приведут к прогрессированию дегенеративно-дистрофического процесса не только ближайшего смежного уровня ПДС.

Исходя из вышесказанного, применяемый нами метод вентральной декомпрессии с применением цилиндрического титанового импланта позволяет сохранить измененный сагиттальный баланс, не вступает в конфликт со смежными уровнями ПДС, препятствуя прогрессированию дегенеративно-дистрофического процесса в выше- и нижележащих сегментах. В дальнейшем, за счет созданного резервного пространства после проведенной декомпрессии позвоночного канала, он может взять на себя нагрузку, проседая с образованием естественного корпородеза между телами позвонков. Именно поэтому мы считаем обоснованным применение цилиндрического титанового кейджа при вентральной декомпрессии в лечении дегенеративных стенозов поясничного отдела позвоночника.