Обоснование схемы активного фильтра гармоник на основе гибридного каскадного инвертора

В настоящее время перспективным средством повышения качества электроэнергии (КЭ) являются активные фильтры гармоник (АФГ), в которых применяются запираемые полупроводниковые приборы. При соответствующем законе управления осуществляется генерирование управляемых высших гармоник в противофазе с фактическими гармониками полупроводниковых преобразователей, что позволяет получить практически синусоидальную форму напряжения сети.

На рис. 1 показана блок-схема базового активного фильтра гармоник, который подключен параллельно с системой шин низкого напряжения 0,4 кВ с целью фильтрации высших гармоник напряжения и тока, вызванных нелинейной нагрузкой.

Рис. 1. Блок-схема базового активного фильтра гармоник

В данной статье предложена схема активного фильтра гармоник на основе гибридной топологии многоуровневых инверторов, позволяющая обеспечить нормативные показатели качества электроэнергии в системе электроснабжения при наличии нелинейной нагрузки.

Гибридная топология многоуровневого инвертора

Одним из достоинств многоуровневого инвертора по сравнению с двухуровневым заключается в том, что в схеме возможно получить высокое напряжение на выходе, используя стандартные низковольтные полупроводниковые элементы, такие как IGBT-модули, не прибегая к необходимости высоковольтных дорогостоящих полупроводников. Другим преимуществом многоуровневого инвертора является многоступенчатость кривой выходного напряжения, что позволяет уменьшить содержание высших гармоник в кривой выходного напряжения. С увеличением количества уровней уменьшаются ступени выходного напряжения и улучшается его качество [1].

Многоуровневые топологии можно разделить на три основные категории: с фиксированной нейтральной точкой, с плавающими конденсаторами и многоуровневый каскадный инвертор [2]. С увеличением количества уровней в инверторе усложняется схема, увеличивается количество полупроводниковых ключей. Поэтому представляют интерес топологии, которые позволяют получить увеличение уровней напряжения с уменьшением количества полупроводников, повысить производительность и надежность системы [3].

Гибридная топология заключается в том, что в гибридном каскадном инверторе несколько ячеек инвертора разных типов соединены последовательно в каждой фазе. Эти инверторные ячейки обычно представляют собой стандартные низко- уровневые инверторы, такие как однофазный инвертор по схеме H-моста, двухуровневый инвертор и трехуровневый инвертор с фиксированной нейтральной точкой (NPC) [4]. Иными словами, гибридные топологии – это топологии многоуровневых инверторов, основанные на применении существующих топологий для отдельных ячеек инвертора. Такое построение многоуровневого инвертора позволяет уменьшить содержание высших гармоник в выходном напряжении без увеличения количества силовых устройств [5–9].

Каждый силовой модуль этой гибридной структуры может работать при определенном напряжении постоянного тока и частоте переключения, что позволяет повысить эффективность работы инвертора. Использование ШИМ для управления инвертором позволяет:

• а)    работать с более низкими частотами преобразования [10, 11];

• б)    обеспечить селективное исключение низкочастотных составляющих в спектре выходного напряжения [12, 13];

• в)    минимизировать коэффициент гармоник тока [14], напряжения [15];

• г)    минимизировать потери в двигателе [16];

• д)    минимизировать среднеквадратичное отклонение напряжения от желаемой формы [17].

Топология, обсуждаемая в этой статье, представляет собой гибрид трехуровневого инвертора с фиксированной нейтральной точкой (NPC) и двухуровневого инвертора (H-мост), соединенных последовательно.

Схема однофазной двухуровневой ячейки H-моста показана на рис. 2а. В этой схеме выходное напряжение Va имеет два значения: +VDC и –VDC. Для получения уровня напряжения +VDC должны быть включены ключи S1 и S4; для получения уровня напряжения –VDC должны быть включены ключи S2 и S3.

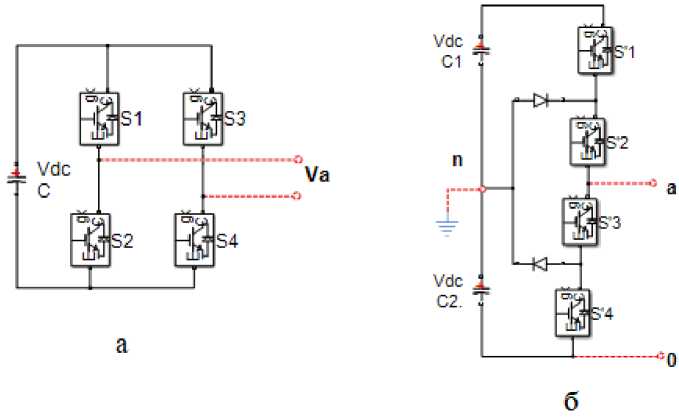
Рис. 2. Топологии однофазных двухуровневой ячейки H-моста (а) и трехуровневой инверторной цепи с фиксированной нейтральной точкой (б)

Трехуровневый инвертор с фиксированной нейтральной точкой для одной фазы показан на рис. 2б. Схема содержит два последовательно соединенных конденсатора C1 и C2. Средняя точка двух конденсаторов n может быть определена как нейтральная точка. Выходное напряжение Van между точками a и n имеет три состояния: –VDC, 0 и +VDC. Для получения уровня напряжения +VDC должны быть включены ключи S'1 и S'2; для получения уровня напряжения –VDC должны быть включены ключи S'3 и S'4; для получения уровня напряжения 0 должны быть включены S'2 и S'3.

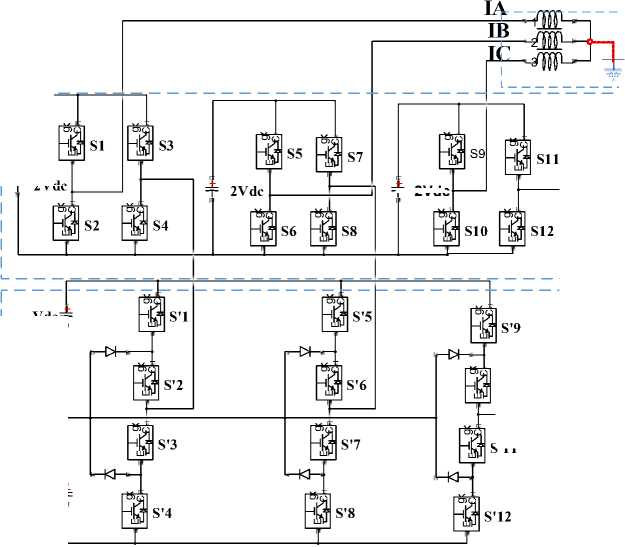
На основе однофазных схем, приведённых на рис. 2, получим трехфазную структуру гибридного инвертора, показанную на рис. 3. В каждой фазе имеется восемь полупроводниковых ключей. Управляющие импульсы на 8 ключей фазы A, фазы B и фазы C подаются со сдвигом фазы на 120 эл. градусов к соответствующей клемме затвора.

В табл. 1 приведены состояния ключей S и S' для одной фазы напряжения U 0A нагрузки инвертора в случае предлагаемой топологии гибридного инвертора. На рис. 4 показаны графики последовательности состояния ключей S и S' во времени и соответствующие им уровни напряжения нагрузки для одной фазы напряжения U_0A в случае предлагаемой топологии гибридного инвертора.

Предложенная топология гибридного инвертора позволяет получить 9 значений фазного напряжения нагрузки и тем самым получить кривую выходного напряжения, близкую к синусоиде. Это делает возможным снижение частоты переключения и снижения скачков напряжения на силовых компонентах.

2Vdc

2Vdc

S'10

Vdcт

Vdc. т

N ! трехфазная

Г" нагрузка

S'11

2- уровневый мост

3-уровневый инвертор

Рис. 3. Трехфазная структура гибридного инвертора, основанная на предлагаемой топологии

Таблица 1

Состояния ключей S и S' для одной фазы напряжения нагрузки инвертора в случае гибридного инвертора

№	Выходное напряжение 1 фазы (U 0A )	S1	S2	S3	S4	S'1	S'2	S'3	S'4
1	4Vdc	1	0	0	1	1	1	0	0
2	3Vdc	1	0	0	1	0	1	0	0
3	2Vdc	0	1	0	1	1	1	0	0
4	Vdc	0	1	0	1	0	1	0	0
5	0	0	1	0	1	0	0	1	1
6	–Vdc	0	1	1	0	0	1	0	0
7	–2Vdc	0	1	1	0	0	0	1	1
8	–3Vdc	1	0	0	1	0	1	0	1
9	–4Vdc	1	0	0	1	0	0	1	1

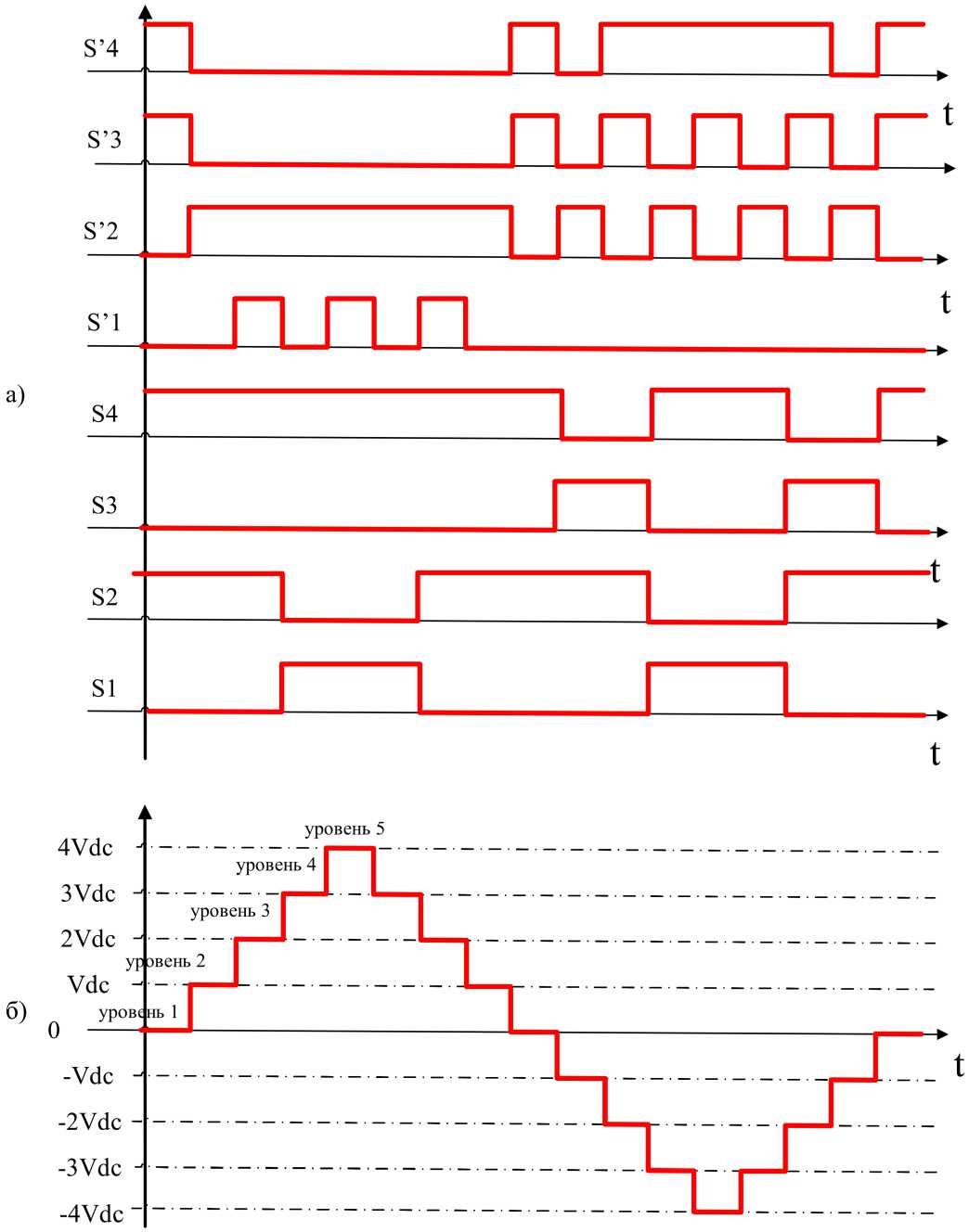
Рис. 4. Последовательность состояния ключей S и S' во времени (a) и соответствующие им уровни напряжения нагрузки для одной фазы U 0A в случае гибридного инвертора (б)

Алгоритм оптимизации напряжения инвертора

Алгоритм оптимизации напряжения инвертора должен обеспечивать поддержание баланса источников напряжения постоянного тока и устранять генерацию синфазного напряжения [9, 18], под которым понимается напряжение между нейтралью источника постоянного тока (точка 0) и нейтралью нагрузки (точка N «земля» нагрузки).

Для управления гибридным инвертором в составе активного фильтра гармоник в работе предложен метод широтно-импульсной модуляции (ШИМ) несущей. Метод широтно-импульсной модуляции используется для уменьшения синфазного напряжения, коммутационных потерь, минимизации гармоник тока и гармоник напряжения [14, 15], получения близкой к синусоидальной волны напряжения и волны тока.

На рис. 5 показана схема подачи управляющих сигналов на полупроводниковые ключи, где ξ x … (x = фаза a, фаза b, фаза c) – управляющий сигнал. Данный управляющий сигнал модулируется в соответствии с алгоритмом, приведённым на рис. 6, и далее сравнивается с треугольной несущей для генерации управляющих импульсов, которые включают или выключают ключи на IGBT-транзисторах (S… и S'…).

На рис. 6 показана блок-схема алгоритма ШИМ, на основе которого осуществляются модуляция управляющих сигналов ξx и затем сравнение их с треугольной несущей для генерации последовательности импульсов, включающих или отключающих 24 полупроводниковых ключа (S…, S'…) в соответствии с табл. 1 и рис. 4.

На блок-схеме алгоритма ШИМ сигнал Vx (x = a, b, c) является напряжением обратной свя- зи от измерительного трансформатора нагрузки [18]:

Va = VAcos 9;

Vb =VBcos( 9 -y);

Vc=Vccos( 9 -y).

Сигнал обратной связи по напряжению нагрузки V x изменяется в зависимости от нагрузки, колеблющейся во времени.

треугольный носитель

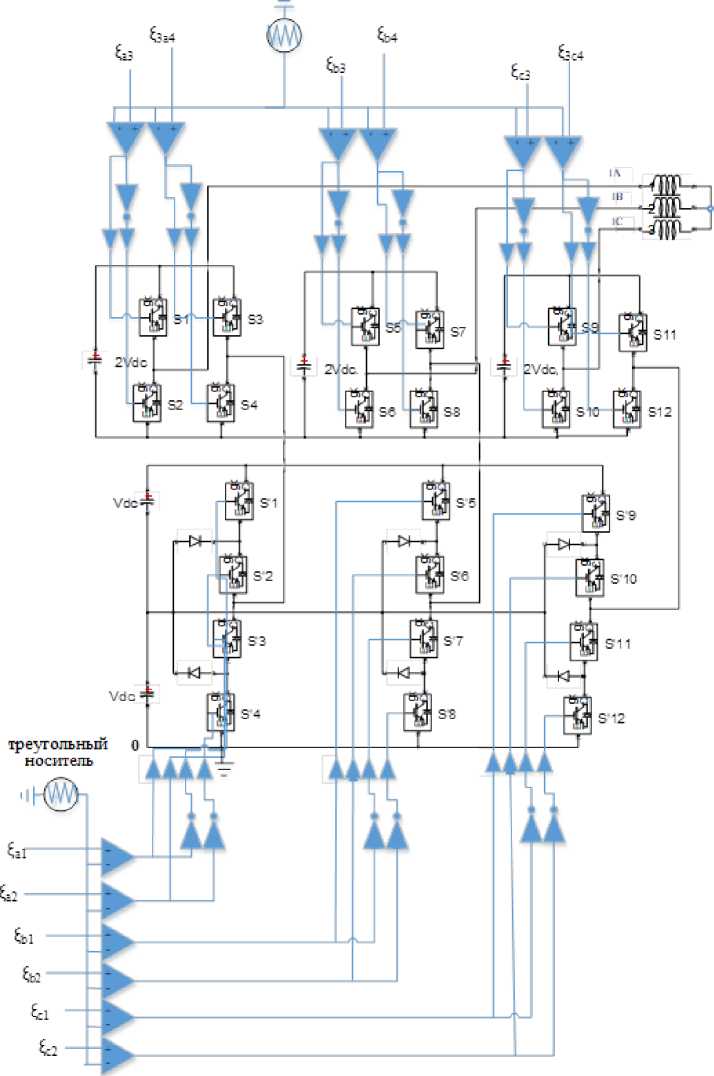
Рис. 5. Схема подачи управляющих сигналов ξx… на полупроводниковые ключи (IGBT-транзисторы)

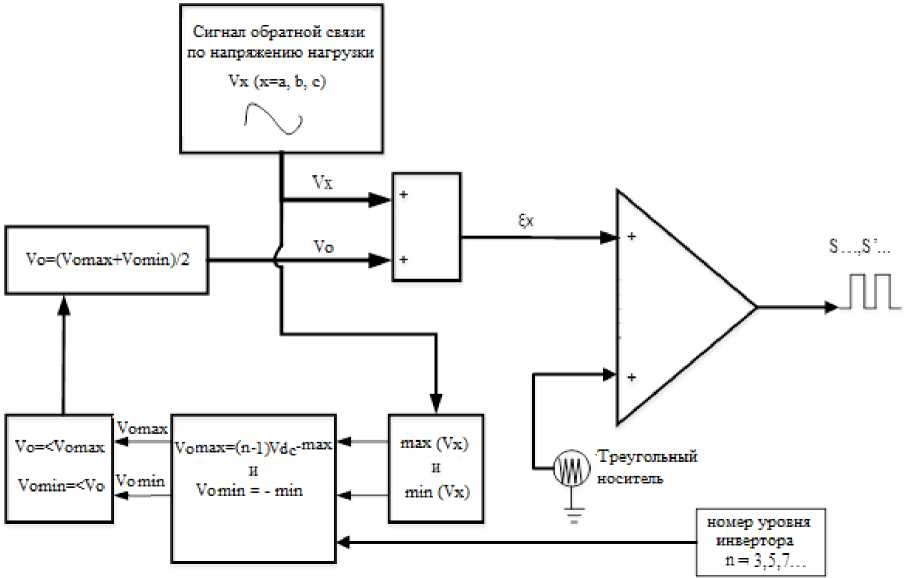
Рис. 6. Блок-схема алгоритма ШИМ на основе несущей для гибридного каскадного инвертора

и, в

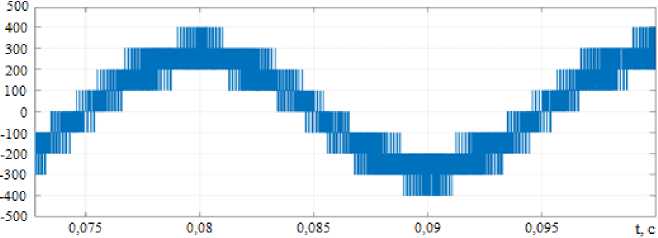
Рис. 7. Выходное напряжение инвертора U0A при отсутствии сигнала V 0 (а) и его наличии (б)

Управляющий сигнал ξx (0 ≤ ξx ≤ 1) равен

^Х = Vx + Vo, где сигнал V0 – синфазное смещение напряжения.

Добавление сигнала V0 к управляющему напряжению Vx позволяет получить сбалансированное, близкое к синусоиде выходное напряже- ние инвертора U0A. Сигнал ξx сравнивается с треугольной несущей (фиксированная установка) для переключения полупроводниковых приборов IGBT.

Значение V 0 находится следующим образом.

Определим величины max и min как макси- мальное и минимальное значения для трехфазных напряжений:

max = max(Va, Vb);

min = min(Va, Vb, Vc).

Запишем неравенство

V^o min — V O — V Omax ,

где Vomax = (n - 1)Vdc - max;    Vomin = -min;

n – номер уровня инвертора; Vdc – напряжение конденсатора постоянного тока.

Отсюда находим V 0 :

у _ (X omax lX omin )

Vo =         2        .

Номер уровня инвертора n = 3, 5, 7…, так как многоступенчатая гибридная инверторная структура генерирует уровни напряжения n > 3 и не содержит четные числа уровней напряжения.

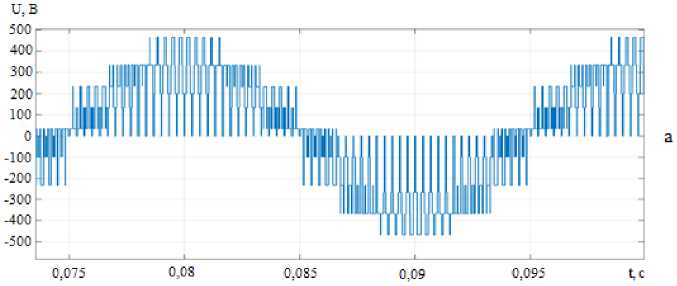
На рис. 3 представлена трехфазная 5-уровневая гибридная инверторная структура на основе предложенной топологии, следовательно, n = 5. На рис. 7 приведены формы выходного напряжения инвертора V0a с одинаковой нагрузкой при отсутствии сигнала V₀ (рис. 7а) и при его добавлении к управляющему напряжению Vx в соответствии с алгоритмом на рис. 6 (рис. 7б). Сравнение выходных напряжений инвертора для этих двух случаев позволяет сделать вывод о том, что добавление сигнала V 0 приводит к сбалансированному выходному напряжению, форма которого близка к синусоидальной.

Модель АФГ и результаты моделирования

Для изучения свойств предложенной структуры АФГ на основе гибридной топологии многоуровневого инвертора и алгоритма его управления разработана модель с использованием пакета MATLAB и его инструментов Sim Power System и Simulink.

На рис. 8 приведена модель трёхфазной системы электроснабжения с нелинейной нагрузкой при включении АФГ. В качестве нелинейной нагрузки взяты частотно-регулируемые электропри- воды общей мощностью 1007 кВт, получающие питание от шин 0,4 кВ. Основу модели АФГ представляет рассмотренный ранее гибридный 5-уровневый каскадный инвертор с использованием ШИМ. Активный фильтр подключен параллельно нелинейной нагрузке.

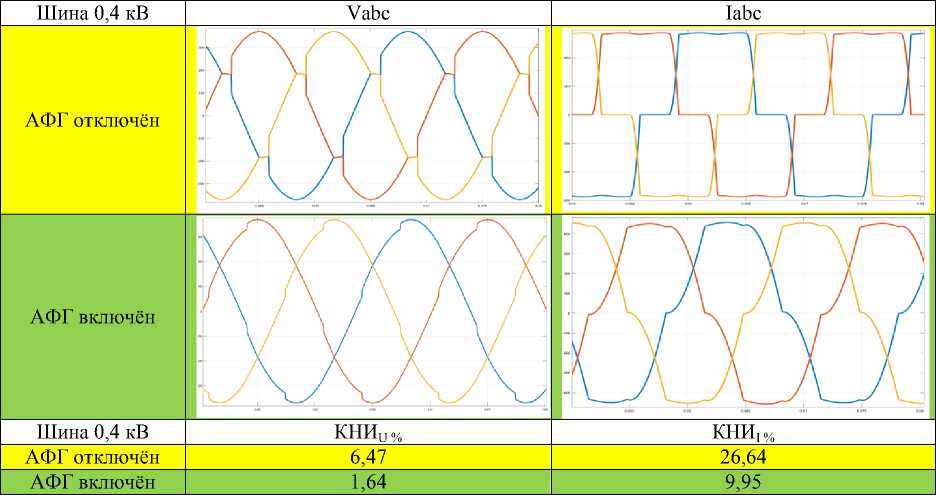
Результаты моделирования приведены в табл. 2, где показаны формы кривых фазных напряжений и токов на шинах 0,4 кВ, а также значения коэффициентов нелинейных искажений напряжения КНИU и тока КНИI для этих кривых при отсутствии и включении АФГ.

На основе анализа результатов, приведённых в табл. 2, сделаны следующие выводы.

При наличии нелинейной нагрузки и отсутствии АФГ формы кривых напряжений и токов существенно отличаются от синусоидальной. Коэффициент нелинейных искажений напряжения на шине низкого напряжения 0,4 кВ равен КНИ_U = 6,47 %. Коэффициент нелинейных искажений тока КНИ_I = 26,64 %. Данные значения существенно превышают допустимые пределы КНИ_U ≤ 5 %, КНИ_I ≤ 20 %, установленные международным стандартом IEEE ST519-2014 [19].

При наличии нелинейной нагрузки и включении АФГ формы кривых напряжений и токов приближаются к синусоидальной форме. В этом случае коэффициент нелинейных искажений напряжения на шине низкого напряжения 0,4 кВ уменьшился с 6,47 до 1,64 %. Коэффициент нелинейных искажений тока уменьшился с 26,64 до 9,95 %. Данные значения меньше допустимых норм, установленных международным стандартом IEEE ST519-2014 [19].

Таким образом, АФГ на основе 5-ступенчатого гибридного инвертора при управлении методом широтно-импульсной модуляции ШИМ является эффективным средством фильтрации высших гармоник на шинах низкого напряжения 0,4 кВ при наличии нелинейной нагрузки.

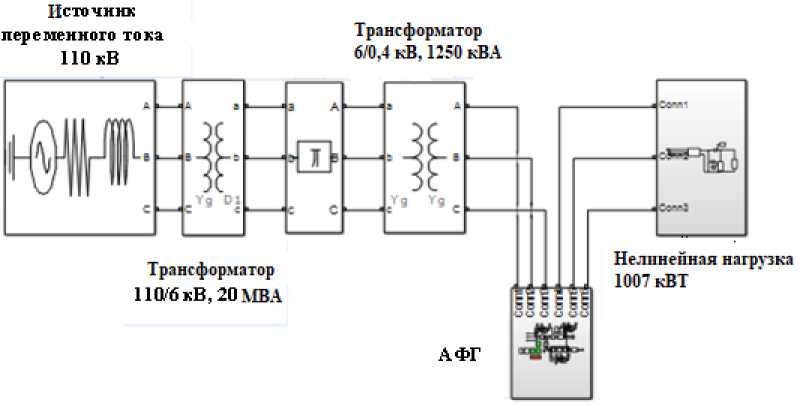
Рис. 8. Модель системы электроснабжения с нелинейной нагрузкой при включении АФГ

Таблица 2

Результаты моделирования

Заключение

П ре дл ож ена с х е м а а кт ивно го фил ьтра га рм оник на основе 5-ст у пенча т ого гибри дного и нв е ртора при у пра в л ени и м е тодом широтно -импульсной м од у л яц и и ШИ М д л я с ис те м эл е к трос на б ж ения 0,4 к В п ри не линей ной на гр узке .

В ы п о л н е н о мо д е л и р о ва ни е эле к т ри ч ес ки х си стем с нел и не й ной н агр узкой . Р е з у л ьтаты м оде л ир ован ия п оз в оли л и оц е н и ть эффе кт ивнос ть пр именения активн о г о ф и л ьтра га рм оник д ля у лучшения качества электроэнергии.

А н а ли з р ез у ль т ат о в мо д ел и р о в ан и я п о к азал, чт о п р и н али ч и и н е ли н е й но й н аг р у зк и и о тс у т ствии АФГ ко э ф ф и ц и ен т ы нели н ейн ы х и с кажени й нап р я жен ия и т о к а н а ш и не н и зк о г о н ап р я жен и я 0,4 кВ пр евы шаю т д о пу ст и мы е п р ед елы, у стано влен н ы е междун ар о д н ы м стан д ар т о м I E EE ST519-2014.

Включение активного фильтра гармоник при наличии нелинейной нагрузки приводит к существенному уменьшению уровня высших гармоник напряжения и тока на шине низкого напряжения 0,4 кВ по сравнению со случаем отсутствия АФГ. Коэффициенты нелинейных искажений напряжения и тока не превышают допустимых пределов, установленных международным стандартом IEEE ST519-2014.

Результаты моделирования позволяют сделать вывод, что разработанный активный фильтр гармоник на основе 5-ступенчатого гибридного инвертора при управлении методом широтноимпульсной модуляции ШИМ является эффективным средством фильтрации высших гармоник на шинах низкого напряжения 0,4 кВ при наличии нелинейной нагрузки.