Обоснование учета силы аэродинамического сопротивления при движении частиц по наклонной полке пневматического сепаратора

Фракционирование полидисперсного материала по крупности в пневматических сепараторах осуществляется под действием массовых сил гравитации и инерции и сил сопротивления движению частиц на пересыпных полках и в пространстве между ними.

Если при свободном движении двухфазной среды определяющим фактором разделения ее по размерам или плотности является взаимодействие сил гравитации и аэродинамического сопротивления, то при движении частиц по наклонной поверхности добавляется сила сопротивления движению или сила трения о поверхность полки.

Существует мнение, что сила трения движения частицы по плоскости в спокойной газовой среде во много раз превосходит силу аэродинамического сопротивления и последней можно пренебречь [1–4].

В случае если поверхность обдувается встречным газообразным потоком, аэродинамическое сопротивление частиц в расчетах, наоборот, учитывается [5, 6].

Таким образом, обсуждение данного вопроса является актуальным и востребованным.

Методы и принципы исследования

Рассмотрим пневматический сепаратор с обратным потоком воздуха через решетку [7, 8], предназначенный, например, для фракционирования материала размером 50–1000 мкм. Части-– 143 – цы разделяемого материала движутся сверху вниз по решетке, образованной параллельными пластинами с длиной полки до 100 мм, мелкие фракции при пересыпке с полки на полку захватываются потоком внутрь аппарата, крупные разгружаются с нижней ее части. Расстояние между жалюзи намного превышает размер частиц, воздушный поток входит без поворота, поэтому у поверхности пластин скорость потока можно считать близкой к нулевой.

Так как частица движется по наклонной полке, проецируем имеющиеся силы на ось, параллельную плоскости движения. Дифференциальное уравнение примет вид:

m — = ^ “ ^) ^s’^{na _} ^p ^_ Fc                                (1)

где m – масса шарообразной частицы; v – скорость ее движения по полке; G – сила тяжести; A – сила Архимеда; F тр – сила трения движения частицы по полке; F с – сила аэродинамического сопротивления; α – угол наклона полки.

После преобразований dv   p4 — p                  3v2 p

^r = g——sma-fgcosa-Q-——.                  (2)

at р_ч                          4 cl р_ч

Здесь g – константа ускорения свободного падения; ρ – плотность дисперсионной среды; ρ_ч – кажущаяся плотность частиц; f – коэффициент трения частицы по полке; d – диаметр шарообразной частицы.

Коэффициент аэродинамического сопротивления для переходной зоны чисел Рейнольдса можно вычислить по зависимости [9].

C_d = — (0,92 + O,147Re⁰'⁵⁵) ' .                                       (3)

Re

Согласно [6] даже сферические частицы имеют трение качения с проскальзыванием. Для частиц, отличающихся по форме от шара, трение о наклонную поверхность имеет сложный физический характер. Будем считать, что коэффициент f в уравнении (2) – это некоторый обобщенный коэффициент трения частицы о поверхность полки, включающий как трение качения, так и трение скольжения.

Результаты математического моделирования

Определяющим фактором процесса фракционирования частиц в жалюзийном сепараторе является их начальная скорость схода с полки в движущийся газовый поток. Ее можно рассчитать, решая уравнение (2) численными методами, например Рунге-Кутты с начальными условиями: t = 0; x = 0; v = 0. Угол наклона полки 45 градусов к горизонту, длина полки 100 мм. Проведенные расчеты показали, что в исследуемом диапазоне параметров:

50 ≤ d ≤ 1000 мкм, ρ ч = 2600 кг/м³, ρ = 1,2 кг/м³, f = 0,15 при угле наклона полки 45 градусов к горизонту скорость частиц увеличивается с длиной пробега по наклонной полке увеличивается, причем для тонких фракций она выходит на постоянное значение (рис. 1).

Если не учитывать аэродинамическое сопротивление частиц, уравнение (2) можно решить в явном виде

(Рч~ Р\ v = gt------sin a — f cos a I;(4)

У 0- (—--—f

• 2 V P4/

На рис. 1 зависимость скорости частиц, рассчитанной без учета сопротивления газовой среды от длины полки, обозначена цифрой 6. Эта кривая инвариантна к размеру частиц, а конечная скорость схода частиц с полки длиной 100 мм составляет около 1,08 м/с.

Для частиц 1000 мкм (линия 5) расчетная скорость их движения с учетом сопротивления воздуха составляет около 1,06 м/с, что сопоставимо с кривой 6. Чем меньше размер частиц, тем больше это различие. Это связано с тем, что, например, для частиц с размером 50 мкм (линия 1) установившаяся скорость движения 0,117 м/с становится на длине полки около 10 мм, для частиц с диаметром 200 мкм (линия 3) постоянная скорость устанавливается на длине более 1500 мм, а для частиц крупнее 1000 мм – более 17000 мм.

На рис. 2 представлена зависимость относительного отклонения скоростей частиц при сходе с наклонной полки длиной 100 мм, рассчитанных с учетом силы сопротивления газовой среды и без ее учета от величины коэффициента трения частицы о поверхность полки.

Как видно из графика, для исследуемого диапазона параметров относительное отклонение для частиц 1000 мкм при учете и без учета сопротивления газовой среды составляет около 3 % при изменении коэффициента трения частиц о поверхность полки до 0,75 и в дальнейшем монотонно возрастает до 10 %. Для других фракций наблюдается похожий характер, при этом

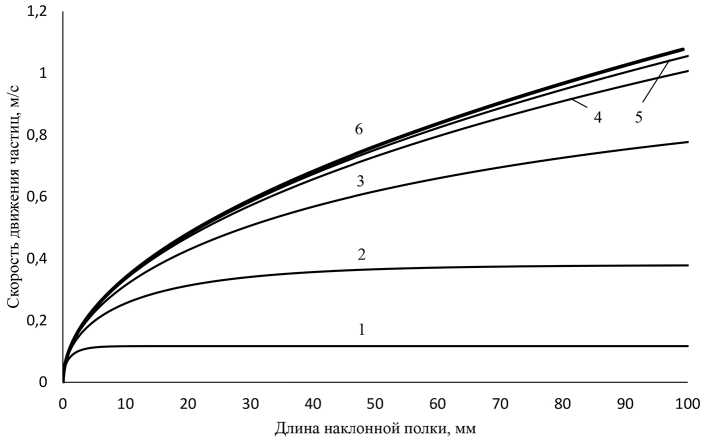
Рис. 1. Изменение скорости движения частиц при движении по наклонной полке c учетом коэффициента аэродинамического сопротивления: 1 – d = 50; 2–100; 3–200; 4–500; 5–1000 мкм; 6 – скорость движения частиц любого размера без учета сопротивления среды

Fig. 1. Change in the velocity of particles when moving along an inclined shelf taking into account the coefficient of aerodynamic drag: 1 – d = 50; 2–100; 3–200; 4–500; 5–1000 microns; 6 – the speed of movement of particles of any size without taking into account the resistance of the medium

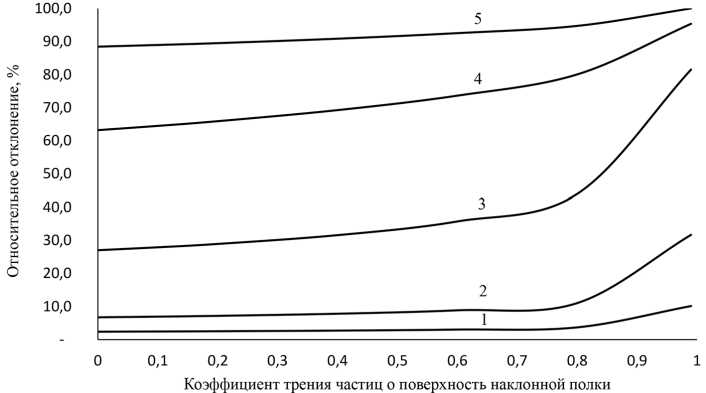
Рис. 2. Изменение относительного отклонения скоростей частиц при сходе с наклонной полки длиной 100 мм, рассчитанных с учетом силы сопротивления газовой среды и без ее учета от величины коэффициента трения частицы о поверхность полки: 1 – d = 1000; 2–500; 3–200; 4–100; 5–50 мкм

Fig. 2. Change in the relative deviation of particle velocities when descending from an inclined shelf with a length of 100 mm, calculated taking into account the resistance force of the gas medium and without taking it into account from the value of the coefficient of friction of the particle on the shelf surface: 1 – d = 1000; 2–500; 3–200; 4–100; 5–50 microns относительные отклонения тем выше, чем меньше размер частиц. Если не учитывать сопротивления газовой среды для частиц 50 мкм, относительная погрешность в расчетах скоростей составит до 100 %.

Выводы

В инженерных расчетах технологического оборудования, в котором осуществляются процессы движения частиц сыпучего материала по наклонным поверхностям, можно не учитывать аэродинамическое сопротивление газовой среды для частиц крупнее определенного размера. Так, для воздушного сепаратора с наклонной решеткой [7] таким размером являются частицы крупнее 1000 мкм. Для более тонких фракций частиц учет сопротивления газовой среды является необходимым условием.

Относительная погрешность в расчетах при игнорировании силы сопротивления газовой среды увеличивается с уменьшением размера частиц, причем с ростом абсолютного значения коэффициента трения частиц о поверхность наклонной полки относительные погрешности возрастают еще больше.

Проведенные в данной работе вычисления относятся к шарообразным частицам, несомненно, возникает интерес, какие будут отличия в расчетах для сыпучих материалов, не имеющих сферической формы.