Обоснование выбора конструкции питателя роторного снегоочистителя, исходя из условий эксплуатации
Автор: Алешков Денис Сергеевич, Корчагин Павел Александрович, Тетерина Ирина Алексеевна, Хирьянов Евгений Викторович
Рубрика: Расчет и конструирование
Статья в выпуске: 2 т.23, 2023 года.
Бесплатный доступ
Проектная деятельность в области машиностроения должна быть обеспечена наличием относительно простых соотношений, на основании которых можно делать выводы об эффективности, ресурсном состоянии или о вариантах применения рабочих органов строительно-дорожных машин. Наличие таких показателей дает возможность делать обоснованный выбор в пользу той или иной конструктивной схемы, геометрических и кинематических параметров рабочих органов машин, в том числе роторных снегоочистителей. Таким образом, задача, поставленная при проведении исследования, в первую очередь, заключается в необходимости оценить возможность обоснования эффективности внедрения и применения каких-либо конструкторских решений на ранних стадиях проектирования машин, что, в свою очередь, подразумевает решение таких вопросов, как обоснование показателей, на основе которых будет даваться оценка об эффективности и описание механизма получения их расчетных значений. В результате проведенных исследований были получены аналитические выражения вырезаемых объемов снежной массы горизонтальной и вертикальной фрезами питателя роторного снегоочистителя. Произведена оценка времени транспортирования вырезанной снежной массы. Показана степень влияния ряда конструктивных и технологических параметров на величину вырезаемой снежной массы и время ее транспортирования. В результате исследований определена область значений, в которой длина траектории вырезания снежной массы для горизонтальной фрезы меньше длины траектории вырезания снежной массы для вертикальной фрезы.
Снегоочиститель, ротор, снежный массив, питатель, эффективность, конструктивные параметры, технологические параметры
Короткий адрес: https://sciup.org/147240894
IDR: 147240894 | УДК: 629.464.4 | DOI: 10.14529/engin230204
Текст научной статьи Обоснование выбора конструкции питателя роторного снегоочистителя, исходя из условий эксплуатации
Проведенные ранее исследования позволили сформировать ряд критериев высшего и низшего уровней, исходя из которых, можно судить об эффективности работы строительно-дорожной машины [1–3]. Из общей группы критериями высшего уровня можно считать: экономическую эффективность, удельную энергоемкость, потребляемую мощность и производительность. Кроме этого, введено понятие четвертого измерения - времени работы элемента рабочего оборудования, которое является неотъемлемой частью критериев высших иерархических уровней [2, 4, 5]. Использование критериев высшего иерархического уровня обладает существенным недостатком, связанным со сложностью их определения, а именно, с решением сложных уравнений динамики рабочего органа и большими затратами машинного времени, либо с существенной трудоемкостью при проведении экспериментальных исследований [1, 6].
Большинство критериев нижнего иерархического уровня не позволяют в полной мере оценить перспективность конструкции роторного снегоочистителя. Кроме этого, выбор основных конструктивных и технологических параметров питателя роторного снегоочистителя в существующих методиках базируется на эмпирических формулах, которые в ряде случаев не позволяют оценить в полной мере роль того или иного параметра в общей эффективности питателя [7, 8].
Таким образом, представляет определенный интерес наличие относительно простых показателей, на основе которых можно было бы судить о техническом совершенстве разрабатываемой конструкции роторного снегоочистителя.
Основная часть
Для суждения о степени эффективности конструкции питателя роторного снегоочистителя воспользуемся кинематическими уравнениями, описывающими движения произвольной точки кромки ленты фрезы горизонтального и вертикального питателя роторного снегоочистителя [9].
Данные уравнения представим в параметрическом виде в системе координат, представленной на рис. 1, 2 и 3 соответственно.
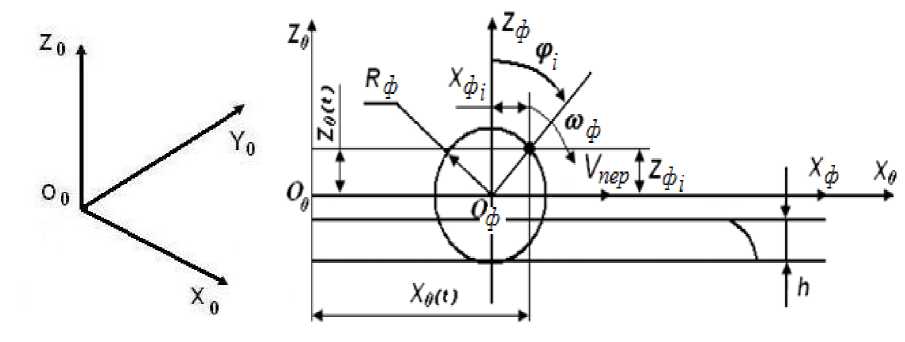
Рис. 1. Расчетная схема для определения траектории движения i -й точки фрезы в плоскости X 0 O 0 Z 0 (вид сбоку)
На расчетной схеме по определению траектории движения i -й точки фрезы в плоскости X 0 O 0 Z 0 (см. рис. 1): R ф - радиус фрезы питателя; h - толщина снежного покрова; Vnep - поступательная скорость роторного снегоочистителя; Ю ф - угловая скорость вращения фрезы питателя роторного снегоочистителя; Х ф, , у ф - координаты положения i- й точки фрезы в системе координат Х ф 0 ф 2 ф [10-12].
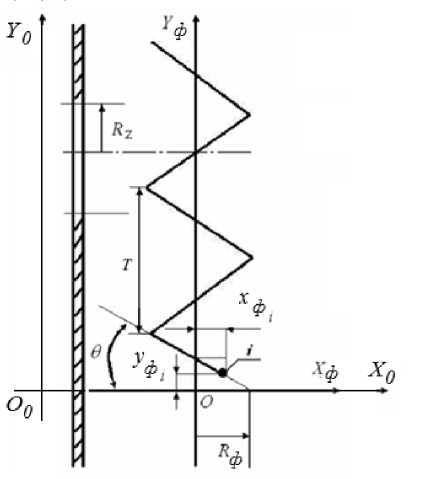
Рис. 2. Расчетная схема для определения траектории движения i -й точки фрезы в плоскости X 0 O 0 Y 0 : 6 - угол захода ленты фрезы, град;
T – шаг винтовой линии ленты фрезы;
R z - радиус загрузочного окна
Уравнение траектории произвольной точки горизонтальной фрезы после ряда преобразований имеет вид [13, 14]:
V nep ’ y 0 i
x =-------+ R - sin-
0i R - to - tg6
ф
y
0 i
R-to -tg6
•
Соответственно, уравнение траектории движения наружной кромки вертикальной режущей полосы в плоскости O0Х 0 Y 0 будет иметь вид:
Vпер x = ——arccos
0 i to
ф
- У •
0 i
Уравнение объема фрезы горизонтального питателя, полученное за счет известного свойства тройного интеграла, при интегрировании системы уравнений имеет вид [6]:
V
W = 4 - n2 - h - tg6 - R - -пер-,
ф ф n - to, зф где 9 - угол захода ленты фрезы, град.
Аналогичный подход использован к вертикальной фрезе питателя роторного снегоочистителя. При этом определены пределы интегрирования:
1) ось х : нижний предел интегрирования равен 0; верхний предел интегрирования имеет вид [15]
V пер y
—— arccos —— + R
to, R
ф
у2- ;
0 i
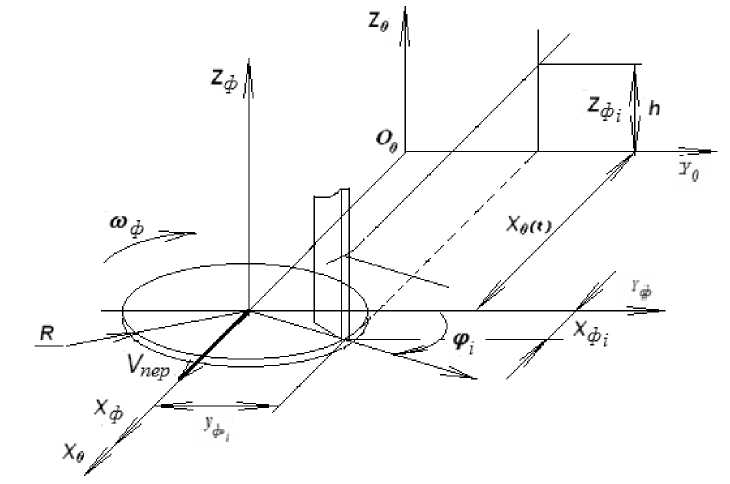
Рис. 3. Расчетная схема для определения траектории движения i- й точки фрезы в пространстве X 0 O 0 Z 0
-
2) ось y : нижний предел интегрирования (с учетом принятой системы координат для одной вертикальной фрезы) равен -R ; верхний предел интегрирования, соответственно R ;
-
3) ось z : нижний предел интегрирования равен 0; верхний равен толщине снежного покрова, h .
В результате интегрирования теоретический объем W , который вырезает i- я вертикальная полоса вертикального питателя из снежного массива, определяется выражением
W = 4. Vnep_.п. r . h, (5)
ωф n где n - количество вертикальных режущих полос вертикального питателя роторного снегоочистителя.
Сравнение формул вырезаемых объемов горизонтальным (3) и вертикальным (5) питателями показывает, что они равны при tg θ=1/π , что соответствует углу захода ленты фрезы горизонтального питателя 9 = 17,7°.
Из вышесказанного следует вывод о том, что при прочих равных условиях ( 9 > 17,7°) горизонтальный питатель вырезает больший объем. Соответственно, при 9 < 17,7° горизонтальный питатель вырезает меньший объем снежной массы из снежного массива по сравнению с вертикальным питателем.
На рис. 4 представлена зависимость изменения вырезаемого объема от угла захода ленты горизонтальной фрезы 9 и отношения Vnep / Ю ф , а также зависимость вырезаемого объема снежной массы вертикальным питателем от аналогичных параметров, при прочих равных условиях.
Вырезаемые объемы снежной массы определены в диапазонах поступательных скоростей роторного снегоочистителя и угловых скоростей вращения фрез, обеспечивающих выполнение условия, описанного в работах [15, 16].
На рис. 5 представлены графические зависимости вырезаемого объема снежной массы вертикальной и горизонтальной фрезами питателей роторного снегоочистителя
Анализ полученных зависимостей показал, что наибольший объем вырезаемой снежной массы можно получить для роторных снегоочистителей с вертикальным расположением фрезы питателя.
Исходя из уравнения траектории резания, возможно определить путь, который пройдет участок рабочего органа от момента захвата снежной массы до момента разгрузки [17].
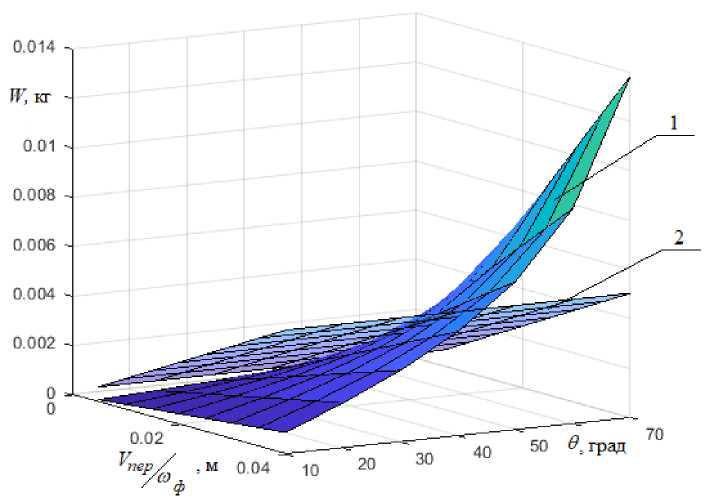
Рис. 4. Зависимость изменения вырезаемого объема снежной массы в зависимости от отношения V пер /ω ф , и угла захода, θ , ленты горизонтальной фрезы:
1 – вырезаемый объем горизонтальной фрезой питателя, W ф ;
2 – вырезаемый объем вертикальной фрезой питателя роторного снегоочистителя, W
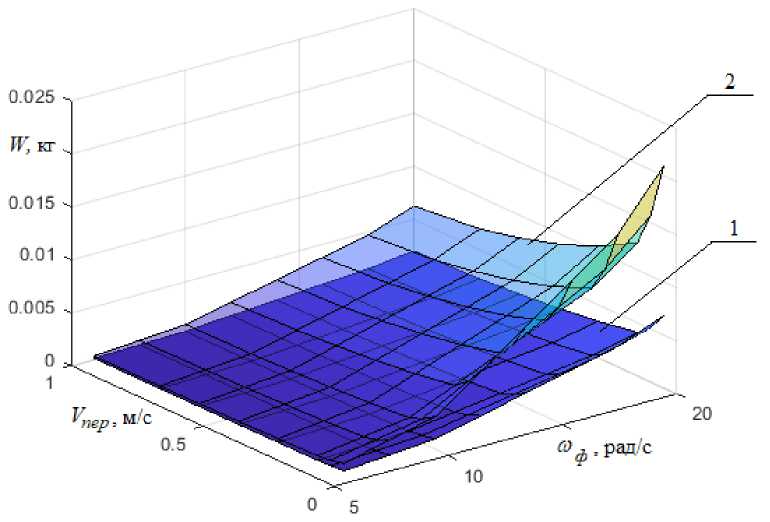
Рис. 5. Зависимость изменения вырезаемого объема снежной массы от поступательной скорости снегоочистителя, V пер , и угловой скорости вращения, ω ф , фрезы питателя, где: 1 – объем, вырезаемый горизонтальной фрезой, W ф ;
2 – объем, вырезаемый вертикальной фрезой, W
Соответственно, для вертикально фрезы питателя с нижним пределом интегрирования t 1 = 0 и верхним пределом интегрирования t 2 = π/ω ф получено:
п! ®, ----------------------------------------------------------- ф 22
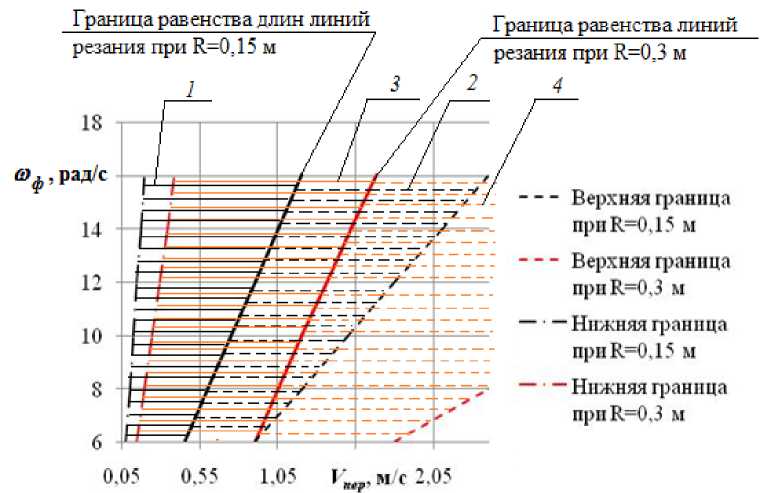
L = Г . I V + R • го, • cos(®, • t) I +1 R • J v ^ пер ф ф j V Ф Ф 'j Интеграл (6) может быть отнесен к эллиптическим интегралам второго рода с последующим выходом на сумму ряда. Последующие результаты были получены в результате численного ин- тегрирования (6) в заданных пределах. Длина траектории движения произвольной точки горизонтальной фрезы L имеет вид: 2π / ω S= ∫ V2+ 2VωR cosωt +ω2R2 cos2ωt + R2⋅ω2⋅ tg2θdt На рис. 6 представлены зависимости длины траекторий L вырезания снежной массы из снежного массива в зависимости от Vпер и ωф. Рис. 6. Зависимость длины траекторий L вырезания снежной массы из снежного массива в зависимости от Vпер и ωф: 1 – горизонтальная фреза; 2 – вертикальная фреза питателя роторного снегоочистителя Из рис. 6 следует, что при скорости роторного снегоочистителя с горизонтальной фрезой питателя более 0,45 м/с длина траектории вырезания снежной массы превышает аналогичный параметр для роторного снегоочистителя с вертикальной фрезой при любых значениях угловой скорости вращения фрезы. Дальнейшее увеличение скорости снегоочистителя ведет к необходимости увеличения ωф и нелинейному росту L для горизонтальной фрезы. Величина траектории L вырезания снежной массы из снежного массива для горизонтальной фрезы превосходит L для вертикальной фрезы [18]. Если учесть, что траектория движения произвольной точки вертикальной фрезы в горизонтальной плоскости эквивалентна траектории точки горизонтальной фрезы в вертикальной плоскости, можно распространить условие наличия точки пересечения траектории, полученное для горизонтальной фрезы, на выбор значений кинематических параметров вертикальной фрезы [19]: V R ≥пер . ω ф Также достаточно очевидным является условие того, что толщина вырезаемой снежной массы должна быть не меньше ширины ленты фрезы bф, т. е. период движения фрезы питателя в поступательном движении фрезерно-роторного снегоочистителя составляет не менее ширины ленты фрезы. При больших значениях толщины вырезаемой снежной массы будут возрастать ее по- тери в питателе при транспортировании к загрузочному окну. С учетом вышесказанного получено выражение V пер b ≤ 2π фω ф . Выражение (9) дает возможность определить нижнюю границу соотношения кинематических параметров питателя роторного снегоочистителя, ниже которой питатель не будет загружен в полном объеме. Представляет определенный интерес совместное рассмотрение условий (8), (9) и границ эквивалентных длин траекторий вырезания снежной массы горизонтальной и вертикальной фрезами питателя роторного снегоочистителя с позиций определения областей приемлемости той или иной конструктивной схемы питателя. На рис. 7 представлены границы областей значений Vпер и ωф, ниже которых длина траектории вырезания снежной массы горизонтальной фрезой питателя роторного снегоочистителя превышает длину траектории вырезания вертикальной фрезой, вычисленная для R = 0,15 м и R = 0,3 м. Рис. 7. Области соотношений кинематических параметров Vпер и ωф, обеспечивающих выполнение условий относительно границы равной длины траекторий резания Кроме прочего, на рис. 7 представлены области соотношений Vпер и ωф, удовлетворяющих выражениям (8), (9): 1 – рекомендуемая область соотношений кинематических параметров Vпер и ωф, обеспечивающих выполнение условий выражений для горизонтальной фрезы R = 0,15 м, длиной линии резания меньшей, чем у вертикальной фрезы; 2 – рекомендуемая область соотношений кинематических параметров Vпер и ωф, обеспечивающих выполнение условий выражений для вертикальной фрезы R = 0,15 м, длиной линии резания меньшей, чем у горизонтальной фрезы; 3 – рекомендуемая область соотношений кинематических параметров Vпер и ωф, обеспечивающих выполнение условий выражений для горизонтальной фрезы R = 0,3 м, длиной линии резания меньшей, чем у вертикальной фрезы; 4 – рекомендуемая область соотношений кинематических параметров Vпер и ωф, обеспечивающих выполнение условий выражений для вертикальной фрезы R = 0,3 м, длиной линии резания меньшей, чем у горизонтальной фрезы [20]. Уравнения регрессии траекторий вырезания равной длины имеют вид: – при R = 0,15 м: ωф =13,33 ⋅ Vпер , (10) – при R = 0,3 м: ωф=12,79⋅Vпер - 5,44. (11) Из рис. 7 следует, что для каждого из рассматриваемых видов питателей роторного снегоочистителя можно определить свою область значений кинематических параметров фрезы питателя, при которых линия траектории резания меньше. Это дает основания предположить о том, что в данных областях соответствующие питатели будут эффективнее, в том числе и по критериям эффективности более высоких иерархических уровней. Рекомендуемой областью выбора кинематических параметров Vпер и ωф для горизонтальной фрезы питателя является область, ограниченная условием (9) и границей равенства линий резания. Для вертикальной фрезы рекомендуемой областью выбора значений Vпер и ωф является область, ограниченная границей равенства линий резания – снизу и условием (8) – сверху. Представленная граница равных длин траекторий вырезания снежной массы для вертикального и горизонтального питателей позволяет судить о возможностях интенсификации работы питателей с горизонтальной и вертикальной фрезами за счет увеличения их поступательных скоростей и угловых скоростей вращения. Дополнительно необходимо отметить, что с увеличением радиуса фрезы R граница равенства линий резания смещается в сторону увеличения значений кинематических параметров Vпер и ωф питателя, а сами диапазоны варьирования параметров Vпер и ωф становятся шире. Заключение Сравнение теоретических значений вырезаемых объемов горизонтальной и вертикально расположенной фрезами роторного снегоочистителя позволяет сделать вывод о потенциальных возможностях питателей. При углах захода фрезы θ меньше 17,7° горизонтальный питатель роторного снегоочистителя вырезает меньший объем снежной массы, чем вертикальный питатель при прочих равных условиях. Полученные уравнения длин траекторий движения произвольной точки фрезы как для вертикального, так и для горизонтального ее расположения позволяют определить продолжительность взаимодействия транспортируемой снежной массы и рабочего оборудования от момента ее захвата до момента ее разгрузки. Установлено, что существует область значений Vпер и ωф, в которой длина траектории вырезания снежной массы для горизонтальной фрезы меньше длины траектории вырезания для вертикальной фрезы. Увеличение значений Vпер и ωф приводит к нелинейному росту длины траектории вырезания снежной массы для горизонтальной фрезы, и ее значение уже превышает аналогичный параметр для вертикальной фрезы. Исследование выполнено за счет гранта Российского научного фонда № 23-29-10014, 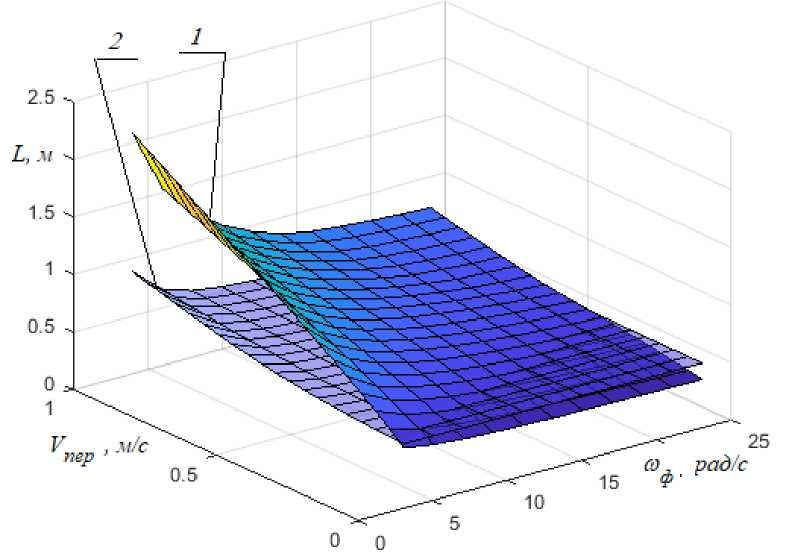
Список литературы Обоснование выбора конструкции питателя роторного снегоочистителя, исходя из условий эксплуатации
- Баловнев В.И., Данилов Р.Г. Pomopnbie снегоочистители // Стpоитeльныe и доpожныe машины. 2019. № 6. С. 10-20.
- Denisova L., Meshcheryakov V. Predictor-based adaptive control system with stability analysis // IFAC-Papers On Line. 2019. № 52(13). С. 486-491. DOI: 10.1016/j.ifacol.2019.11.110.
- Gerling B., Herwijnen van Alec, Löwe H. Measuring the Elastic Modulus of Snow. // Geophysical Research Letters. 2017. С. 44. DOI: 10.1002/2017GL075110.
- Ovsyannikov V., Nekrasov R., Putilova U., Il'yaschenko D., Verkhoturova E. On the issue of automatic form accuracy during processing on CNC machines // Revista Facultad de Ingenieria. 2022. № 103. С. 88-95. DOI: 10.17533/udea.redin.20201111.
- Du Sen, Petrie John, Shi Xianming Use of Snow Fences to Reduce the Impacts of Snowdrifts on Highways: Renewed Perspective // Transportation Research Record: Journal of the Transportation Research Board. 2017. Vol. 2613. P. 45-51. DOI: 10.3141/2613-06.
- Boote D., Vergassola G., Di Matteo V. Strength Analysis of Superyacht Superstructures with Large Openings // International Review of Mechanical Engineering (IREME). 2017. Vol. 11 (1). Р. 1-9. DOI: 10.15866/ireme.v11i1.9289.
- Трофимова И.Ф., Баловнев В. И. Плужный снегоочиститель для скоростной очистки автомобильных дорог от снега // Технология колесных и гусеничных машин. 2015. № 4. С. 49-55.
- Дудкин М.В., Ким А.И., Молдаханов Б.А., Роговский, В.В. Определение усилий на рабочем органе фрезерно-роторного снегоочистителя //Труды университета. 2022. № 2(87). С. 16-22. DOI: 10.52209/1609-1825 2022 2 16.
- Bobillier G., Bergfeld B., Capelli A., Dual J., Gaume J., Herwijnen van Alec and Schweizer J. Micromechanical modeling of snow failure // The Cryosphere. 2020. № 14. P. 39-49. DOI: 10.5194/tc-14-39-2020.
- Denisova L. A., Meshcheryakov V. A. Control systems design: the technology of stochastic perturbations simulation // Journal of Physics: Conference Series. 2018. Vol. 1050, № 1. С. 012020. DOI: 10.1088/1742-6596/1050/1/012020.1.
- Kang L., Zhou X., Hooff T., Blocken B., Gu M. CFD simulation of snow transport over flat, uniformly rough, open terrain: Impact of physical and computational parameters // Journal of Wind Engineering and Industrial Aerodynamics. 2018. № 177. С. 213-226. DOI: 10.1016/j.jweia.2018.04.014.
- Mikheyev V.V. Generator of periodic inertia force concentrated in one direction // Journal of Physics: Conference Series. XIII International Scientific and Technical Conference "AppliedMechanics and Systems Dynamics". 2020. С. 012106. DOI: 10.1088/1742-6596/1441/1/012106.
- Дудкин М.В., Молдаханов Б.А., Бугаев А.Б. Классификация методов повышения эффективности работы питателей шнеко- и фрезерно-роторных снегоочистителей // Вестник Восточно-Казахстанского государственного технического университета им. Д. Серикбаева. 2022. № 2. С. 67-70. DOI 10.51885/1561-4212 2022 2 64.
- Плотникова В.А., Калёнов К.А., Захаров Д.П. Обзор снегоочистителей роторного типа // Автоматизированное проектирование в машиностроении. 2022. № 13. С. 43-47. DOI: 10.26160/2309-8864-2022-13-43-47.
- Azieva L.D. Examples of solving problems for the heat equation in Mathlab // Trends in the development of science and education. 2020. С. 8-11. DOI: 10.18411/lj-07-2020-23.
- Bartenev I., Malyukov S., Malyukova M. Forest fire extinguishing: theoretical study of the screw drum parameter influence on the efficiency of a forest fire soil-sweeping machine // IOP Conference Series: Earthand Environmental Science. 2020. № 595. С.012013. DOI: 10.1088/17551315/595/1/012013.
- Баловнев В.И., Данилов Р.Г. Снегопогрузчики // Строительные и дорожные машины. 2020. № 1. С. 3-9.
- Aleshkov D.S., Sukovin M.V. Aerodynamic characteristics of the milling and rotary snowblower feeder in the loading gate area // International Review of Mechanical Engineering. 2017. Т. 11. № 9. С. 701-708. DOI: 10.15866/ireme.v11i9.13832.
- Carbone A., Chiaia B. M., Frigo B., Turk C. Multi-scale modeling of snow microstructure // Journal for Multiscale Computational Engineering. 2013. №11(2). С. 177-184. DOI: 10.1615/IntJMultCompEng.2012001697.
- Vasilyev V., Ovsyannikov V., Kovalev R. Optimization of vehicle diagnostic algorithms at equipment design // Advances in Intelligent Systems and Computing. 2020. Т. 1115. С. 677-684. DOI: 10.1007/978-3-030-37916-2 66.


