Обработка дискретных составных частотно-модулированных сигналов посредством нейросетевого анализа

Практика радиолокационных и радиофизических измерений зачастую связана с необходимостью приема и обработки сигналов, представляющих собой последовательности радиоимпульсов с внутриимпульсной частотной модуляцией. До недавнего времени обработка таких сигналов была основана на использовании дисперсионных фильтров сжатия или микрополосковых линий задержки [1]. Процесс сжатия входного радиосигнала осуществляется путем согласованной с частотой внутриимпульсной модуляции задержки его спектральных составляющих с последующим их когерентным сложением. Вместе с тем развитие цифровых технологий обработки сигналов сделало актуальным их применение для решения задачи оптимальной фильтрации сигналов (одиночной и пачечной структуры) с различными видами частотной модуляции.

Особенность построения алгоритма обработки («сжатия») таких сигналов состоит в практической его идентичности алгоритму, который осуществляется в реальных нейронных сетях [2]. В этих сетях функции линий задержки выполняют аксоны нейронов. Экспериментально установлено, что эта скорость колеблется в пределах 10…100 м/с и пропорциональна корню квадратному из толщины аксона [3]. Моделированный аналог такой сети получил название «динамической нейронной сети» [4–6].

Основной особенностью такой нейронной сети (рис. 1), реализованной программно, является наличие обратных связей. Величину временной задержки сигнала на её входе определяют весовые коэффициенты обратных связей Еу. Входной набор дискретных отсчетов X аналогового модулированного сигнала подается на первый слой (где происходит нормировка входного сигнала по амплитуде) нейронной сети, по которым нейронная сеть проходит обучение1. Содержательная сторона обучения связана с подстройкой весовых коэффициентов нейросети, обеспечивающих требуемую задержку. Далее выходной сигнал с первого слоя становится входным сигналом для второго слоя и на первом шаге работы программы запоминается нейронной сетью. На следующих шагах из выходных значений первого слоя будут вычитаться запомненные значения предыдущего шага, умноженные на соответствующие задержке весовые коэффициенты. После каждого шага значения, полученные на каждом нейроне, складываются и подаются на пороговое устройство, а далее на функцию активации. После этого нормированные значения переводятся в изначальные, и мы получаем результат.

Рис. 1. Структурная схема динамической нейронной сети

Динамическая нейронная сеть с временными задержками представляет собой многослойный персептрон с модифицированными узлами (рис. 2).

Каждый из J входов имеет линию задержки на N значений. Сумматор складывает значения,

(1)                                                                     (2)

поступающие с входов y j , и значения, содержащиеся в линиях задержек у £ (р) с учетом весовых коэффициентов W ;j , вычисляет порог и нелинейную активационную функцию.

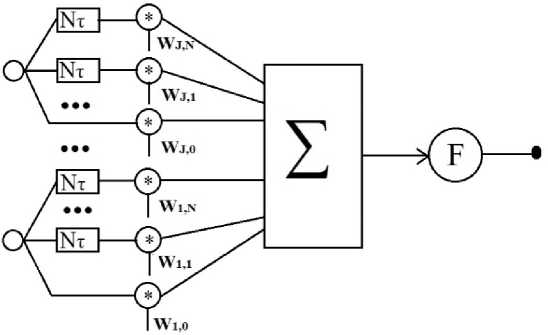
Рис. 2. Узел динамической нейронной сети с временными задержками

На входы сети подается дискретный модулированный сигнал X = (х ; : i = 0... п — 1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

уу(1) = Sj(1) = ^^ОцХ; + Г;) , у = 0... m — 1 ,

Ж - матрица, составленная из весовых коэффициентов нейронов, а m - количество запоминаемых отсчетов. Г ; = min (X) - биас (смещение).

Главная диагональ матрицы Ж полагается нулевой, что означает отсутствие влияния нейронов на самих себя. Веса, заданные таким образом, определяют устойчивые состояния сети, соответствующие запомненным дискретным отсчетам.

После этого полученными значениями инициализируются значения аксонов второго слоя:

yf ) = у«, j = 0... m — 1.

Далее вычисляем новые состояния нейронов второго слоя:

5(2(Р + 1) = Уу(Р) — £; 1^=0 У^Чр) , k*j,j = 0...m-1, р = 0 ... N, где p - количество значений линии задержки в j-м нейроне. Величина Еу рассчитывается нейросетью при обучении с учетом спектральных составляющих сигнала.

И значения их аксонов:

Уу2)(Р +1) = / [$у2)(р + 1)], j = 0 ... m - 1.

Сигмоидальная активационная функция / имеет вид порога, причем величина F (см. рис. 2) должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

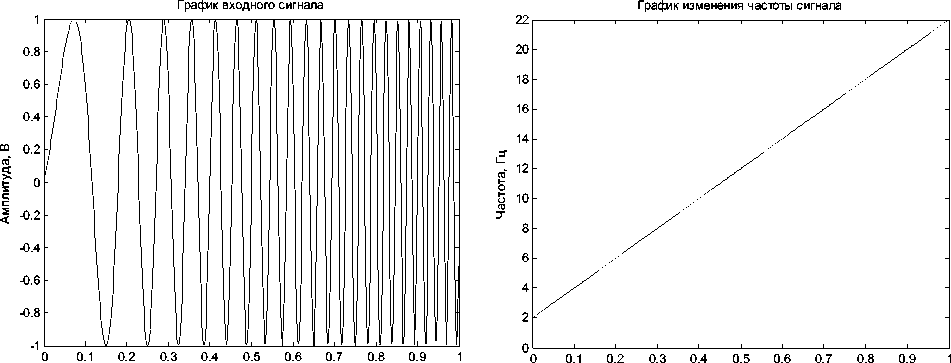
Для примера рассмотрим эффективность указанного выше алгоритма функционирования нейронной сети для «сжатия» одиночного сигнала (рис. 3) с линейной внутриимпульсной частотной модуляцией (рис. 4).

Время, с                                                                   Время, с

Рис. 3. Временная диаграмма входного сигнала        Рис. 4. Изменение частоты входного сигнала

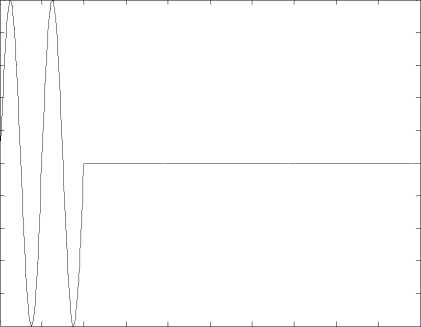
При использовании величин задержки структурных элементов входного сигнала в системе его обработки (см. рис. 1) по закону, обратному изменению частоты (рис. 5), на выходе сумматора (см. рис. 1) получим сигнал (рис. 6), который сжимается по отношению к исходному в К = Т_с • / Д /2 раз², где К - коэффициент сжатия; / Д - девиация частоты входного сигнала; Т _с - длительность сигнала.

При этом происходит увеличение его амплитуды, обусловленное когерентным сложением составляющих сигнала с выхода линий задержек, относящихся как к началу импульса, так и к его концу. Частота выходного сигнала равна средней частоте спектра входного сигнала.

Рассмотренный алгоритм обработки одиночных широкополосных сигналов может быть рапространен на прием и обработку протяженных последовательностей непрерывных или квазинепрерывных сигналов с внутриимпульсной частотной модуляцией (рис. 7).

Для реализации алгоритма обработки таких последовательностей потребуется нейронная сеть с набором блоков временных задержек, обратных по отношению к частоте входного сигнала. Для примера такого сигнала (см. рис. 7) с характерным изменением частоты (рис. 8) результат его нейросетевой обработки (рис. 9) также отражает увеличение амплитуды выходного сигнала и «сжатие» его протяженности по отношению к исходному.

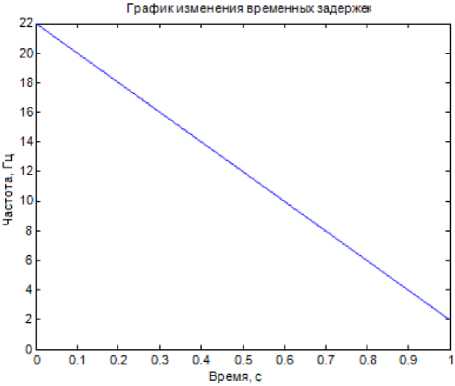
Рис. 5. Изменение временных задержек

График выходного сигнала

I -01

-2

-3

-4

-5

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Время,с

Рис. 6. Сигнал на выходе сумматора

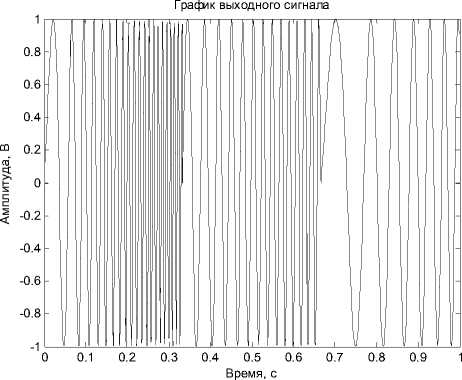
Рис. 7. График входного сигнала

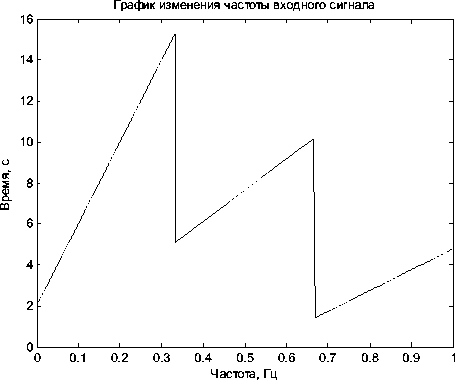
Рис. 8. График изменения частоты сигнала

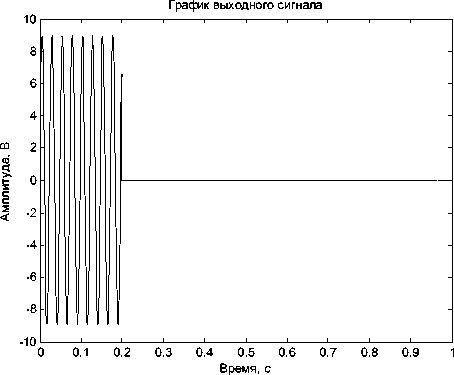
Рис. 9. График выходного сигнала

Полученный результат позволяет сделать вывод о том, что с помощью нейронной сети можно обрабатывать временные последовательности с внутриимпульсной частотной модуляцией. Длительность обработки входной последовательности с внутриимпульсной частотной модуляцией в зависимости от длительности входного сигнала и параметров обучения нейросети составляет в среднем 4–8 с. После завершения процесса обучения нейросети эта длительность сокращается примерно на порядок.

Описанный в статье метод обработки широкополосных сигналов на базе динамических нейронных сетей может быть применен в радиолокации для обнаружения последовательности час-тотно-модулированных сигналов. Возможным методом упрощения реализации рассмотренного алгоритма является разделение сложномодулированной последовательности (см. рис. 8) на дискреты, в пределах которых частота модулирующего колебания изменяется линейным образом. С выхода нейросети для каждого дискрета сигналы детектируются. Дальнейшая их совместная нейросетевая обработка проводится на видеочастоте, аналогично тому, как это осуществляется в реальных нейронных сетях [3].