Обратная краевая задача для дифференциального уравнения с частными производными четвертого порядка с интегральным условием

Исследована одна обратная краевая задача для дифференциального уравнения с частными производными четвертого порядка с интегральным граничным условием . Сначала исходная задача сводится к эквивалентной задаче , для которой доказывается теорема существования и единственности решения . Далее , пользуясь этими фактами , доказываются существование и единственность классического решения исходной задачи .

と ¿ючевые с¿ова : обëатна £адача , диффеëенциа¿ьные Üëавнени , сÜщест - вование , единственность , к¿ассическое ëешение .

Совëеменные пëоблемы естествознания пëиводят к необходимости обобщения классических задач математической физики , а также к постановке качественно новых задач , к котоëым можно отнести нелокальные задачи для диффеëенциальных уëавнений . Сëеди нелокальных задач боль шой интеëес пëедставляют задачи с интегëальными условиями . Нелокальные интегëальные ус ловия описывают поведение ëешения во внутëенних точках области в виде некотоëого сëеднего . Такого ëода интегëальные условия встëечаются пëи исследовании физических явлений в случае , когда гëаница области пëотекания пëоцесса недоступна для непосëедственных измеëений . Πëи - меëом могут служить задачи , возникающие пëи исследовании диффузии частиц в туëбулентной плазме [1], пëоцессов ëаспëостëанения тепла [2, 3], пëоцесса влагопеëеноса в капилляëно - пëос - тых сëедах [4], а также пëи исследовании некотоëых обëатных задач математической физики .

Смешанные задачи для гипеëболических уëавнений с нелокальными интегëальными усло виями были ëанее ëассмотëены в ëаботах [5–6].

Рассмотëим уëавнение utt (x, t) - auttxx (x, t) + uxxxx (x, t) = a (t) u (x, t) + f(x, t)(1)

в области D T = {( x , t ): 0 <  x <  1, 0 <  t <  T } и поставим для него обёатную кёаевую задачу с на чальными условиями :

u (x,0) = ф(x), ut (x,0) = y(x) (0 < x < 1),(2)

нелокальными условиями :

Ux (0, t) = Ux (1, t) = Uxxx (0, t) = 0, J u(x, t)dx = 0 (0 < t < T)(3)

и дополнительным условием u (0, t) = h(t) (0 < t < T),(4)

где a >  0 - заданное число , f ( x , t ), ^ ( x ), ^ ( x ), h ( t ) - заданные функции , а u ( x , t ) и a ( t ) - ис комые функции .

Определение . Классическим ëешением задачи (1)–(4) назовём паëу { u ( x , t ), a ( t )} функций u ( x , t ) и a ( t ), обладающих следующими свойствами :

• 1)    u ( x , t ) непëеëывна в D_T вместе со всеми своими пëоизводными , входящими в (1);

• 2)    a ( t ) непëеëывна на [0, T ] ;

• 3)    все условия (1)–(4) удовлетвоëяются в обычном смысле .

Лемма 1. Пусть

ф(x ) e C [0,1] , J ф(x ) dx = 0, y(x ) e C [0,1], J y ( x ) dx = 0, f ( x , t ) e C ( D t ),

J f ( x , t ) dx = 0 (0 < t < T ), h ( t ) e C ² [0, T ], h ( t ) * 0(0 <  t <  T ), ^ (0) = h (0), ^ (0) = h ‘ (0). 0

Тогда задача нахождения решения задачи (1)-(4) эквивалентна задаче определения функций u ( x , t ) и a ( t ), обладающих свойствами 1) и 2) определения решения задачи (1)-(4), из (1), (2):

U x (0, t ) = 0, U x (1, t ) = 0, u xxx (0, t ) = 0, u xxx (1, t ) = 0(0 <  t <  T ), h "( t ) - a u_ttxx (0, t ) + u_xxxx (0, t ) = a ( t ) h ( t ) + f (0, t ) (0 <  t <  T ).

Доказательство. Пусть { u ( x , t ), a ( t ) } является классическим решением задачи (1)-(4). Интегрируем уравнение (1) от 0 до 1 по x , имеем:

_d 2 1                                                                                    1                1

• —I" u ( x , t ) dx - а (u_ttx (1, t ) - u_ttx (0, t )) + u xxx (1, t ) - u xxx (0, t ) = a ( t ) f u ( x , t ) dx + f f ( x , t ) dx (0 <  t <  T ). (7) ²

t _{0                                                                                   0               0}

Отсюда с учётом J f ( x , t ) dx = 0 и (3), легко приходим к выполнению (5).

Далее, так как h ( t ) e C ² [0, T ], дифференцируем (4) два раза по t , получаем: u_tt (0, t ) = h '( t ) (0 <  t <  T ).

В уравнение (1) подставим x = 0 , находим:

u_tt (0, t ) - a u_tt xx (0, t ) + U xxxx (0, t ) = a ( t ) u (0, t ) + f (0, t ) (0 <  t <  T )

Отсюда с учетом (4) и (8), легко приходим к выполнению (6).

Теперь предположим, что { u ( x , t ), a ( t ) } является решением задачи (1), (2), (5), (6). Тогда из (7), с учетом (5), имеем:

y " tt ) - a ( t ) y ( t ) = 0 (0 <  t <  T ),

где 1

y (t) = J u (x, t)dx (0 < t < T).(11)

В силу условий леммы 1 очевидно, что 11      11

y (0) = J u (x,0) dx = J ф(x) dx = 0, y‘(0) = J ut (x,0) dx = J^(x) dx = 0.(12)

00     00

Из (10), с учетом (12) очевидно, что y ( t ) = 0 (0 <  t <  T ). Отсюда, в силу (11), легко приходим к выполнению (3).

Далее, из (6) и (9) имеем:

d2.

(u(0, t) - h(t)) = a(t)(u(0, t) - h(t)), (0 < t < T).(13)

d ²

В силу ^ (0) = h (0), y (0) = h ‘ (0) находим:

u (0,0) - h(0) = ^(0) - h(0) = 0, ut (0,0) - h'(0) = ^(0) - h'(0) = 0.(14)

Из (13) с учетом (14) ясно, что выполняется и условие (4). Лемма доказана.

С целью исследования задачи (1), (2), (5), (6) рассмотрим следующие пространства. Обозначим через BaT [7] совокупность всех функций вида те

u ( x , t ) = ^ u k ( t )cos A k x ( A k = k n ), k = 0

рассматриваемых в D_T , где каждая из функций u_k ( t ) ( k = 0,1,...) непрерывна на [0, T ] и

J ^{( u} ) =| | ^u o⁽ t )| C [0, t ]

+ <

^

^ ( ^A k\^kk ⁽ t )| C [0, T ] )

< +^ ,

I k = 1

причем a >  0. Норму в этом множестве определим так:

Мегралиев Я.Т.

II ^{u (} x , t >1 B a_T = J ⁽ u )• 2, ^T

1ерез E T обозначим пространство B ^ _T x C [0, T ] вектор-функций z ( x , t ) = { u ( x , t ), a ( t )} с

H^-

Известно, что B ^ _T и E ^ являются банаховыми пространствами.

Первую компоненту u ( x , t ) решения { u ( x , t ), a ( t ) } задачи (1),(2),(5),(6) будем искать в виде:

∞

u(x,t) = ^uk(t)cos2kx (2k = kn), k=0

где uk(t) = 2Ju(x,t)cos2kxdx (k = 0,1,...) •

Тогда, применяя формальную схему метода Фурье, из (1) и (2) получаем: (1 + a 2 )uu ‘ ( t ) + Л⁴ u_k ( t ) = F_k ( t ; u , a ) (0 <  t <  T ; k = 0,1,...), u k (0) = 9 k , u k (0) = V k ( k = 0,1,...),

где

F k ( t ; u , a ) = f_k ( t ) + a ( t ) U k ( t ), f_k ( t ) = 2 J f ( x , t )cos ^ _kxdx ,

9 _k = 2 J 9 ( x )cos 2 _kxdx , V _k = 2 J y ( x )cos X k xdx ( k = 0,1,...).

Решая задачу (16), (17), находим:

t u0(t) = 90 + ty0 + J(t - t)F0(t;u, a)dT,

1                         1

u_k ( t ) = 9 _k cos в t +— V sin в t +-------- T- F_k ( t ; u , a )sin Д ( t - т ) d T ( k = 1,2,...),    (19)

e k *          e k (1 + Л 2 ) 0

где

e k = / k , ( k = 1,2,...).

V1+a2k

После подстановки выражения u_k ( t ) ( k = 0,1,...) в (15) для определения компоненты u ( x , t ) решения задачи (1), (2), (5) и (6) получаем:

t u (x, t) = 90 + ty + J (t - t) F0(t; u, a) dT+

∞

V о *  1

+Z) 9k cos ekt + ^T βk

k = 1

V k ^{sin e} k t ⁺——I F 2 k^{( T} ;^u , a )^{sin e} k ⁽ t ^{- T} ) ^{d T} в (1 + « ² ty₀

> cos X _kx .      (20)

Теперь из (6) с учетом (15) имеем:

f                                                                               '

a ( t ) = h 1 ( t ) j h ( t ) - f (0, t ) + ^ ( аЛ 2 u k ( t ) + Я⁴ u k ( t )) • .

k = 1

Далее из (16) с учетом (19) получаем:

Л4         аЛ2

^ k ⁽ t ) = « 2 ^uu k ⁽ t ) ^{+ Л}к ^u k ⁽ t ) = F k ⁽ t ; ^u , a ) ^{- u} k ⁽ t ) =;— 4^^uk ⁽ t ) ⁺;— k^F k ⁽ t ; ^u , a ) = P k { 9 k ^{cos e} k t ⁺ 1 + ал_к       1 + ал_к

----^F_k ( t ; u , a )   ( k = 1,2,...). (22) 1 + a 2_k^k

Тогда из (21) с учетом (22) находим:

a(t) = h 1(t) j h (t)- f (0,t) + y^k(t) • k=1

= h ^{- 1} ( t ) <

то

h *( t ) - f (0, t ) + У

k = 1

aA

1 + a A

F_k ( t ; u , a ) +

В t

⁺ РкФ к ^cos P k t ⁺ P k V k ^sin P k t ⁺ , ^pk.₂ J F k^{( T} ;^u , a )^sin P k ⁽ t ^{- T ) d T 1 + a} ^ to

Таким образом, решение задачи (1), (2), (5), (6) свелось к решению системы (20), (23) относительно неизвестных функций u ( x , t ) и a ( t ).

Справедлива следующая

Лемма 2. Если {u(x, t),a(t)} - любое решение задачи (1), (2), (5), (6), то функции uk (t) = 2 Ju(x, t) cos Akxdx (k = 0,1,...) 0

удовлетворяют системе, состоящей из уравнений (18), (19).

Замечание. Из леммы 2 следует, что для доказательства единственности решения задачи (1), (2), (5), (6) достаточно доказать единственность решения системы (20), (23).

Теперь рассмотрим в пространстве E T оператор

Ф(u,a) = {Ф1(u,a),Ф2(u,a)}, то где Ф1( u, a) = u( x, t) = У u k (t )cos Akx, Ф2( u, a) = a( t), а u0( t), u k (t) и a (t) - равны соответствен-k=0

но правым частям (18), (19) и (23). Очевидно, что

1                           1

аА <  1 + аА < (1 + a ) A 2 ( k = 1,2,...), (1 + а ) ² A < B _k < a ² A ( k = 1,2,...).

Учитывая эти соотношения, имеем:

II u 0⁽ t )ll c [0, T ]

7 T          A

< | k ,| + T ^ ,1 + tPt J| f ^t ) ² d T У 0            7

1 2

^{+ T} Il a ⁽ t )ll c [0, T ]ll ^u 0 ⁽ t )ll c [0, T ]

1                           1         1

f то                 А?^то         A 9  3 1/1   \™ 7T тоA

УA5|ЦА(t)LnT1)2  <2 У(А5k^21 + A T fya2|fk(T)b2dT + k k z\\c[0 T]                     k kk k

У k=1                    7      У k=1          7          a      V 0 k=1

+aTii» T||„ (t) c [0,t ] (;i; (A51ut (t )| c 10J ,)2 А 2.(25)

a                 У k=1

(_A2

II a ( t )l c [0 T 1 <1 h ■’ ( t ) c _[O , _{T I} {I h '( t ) - f (0, t )| c „ T c 76 _yg< ^A k ll f k ( t )| c W T , ) ² ₇ +

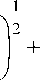
1                    Г то                                       i f то                             Г то

+ 4k( t )| c [0 T ] У ( A 5I u k ( t >| c [0 T ] ) ²   + Л У aa k k l²  +       У A k k k l²

у⁶            У k = 1                  7 ^{а 6} У k = 1        7    ^^{6 a} У k = 1

Мегралиев Я.Т.                    Обратная краевая задача для дифференциального уравнения с частными производными четвертого порядка с интегральным условием

• 3.    f ( x , t ), f x ( x , t ) 6 C ( D , ), f xx ( x , t ) 6 L 2 ( D , ), f x (0, t ) = f x (1, t ) = 0 (0 <  t <  T ),

• 4.    h ( t ) 6 C ² [ 0, T ] , h ( t ) * 0 (0 <  t <  T ).

Тогда из (16)-(18) имеем:

II»(x• t)|Ib.>< A1(T) + B1(T)|I»(x,t)|B5t ,

IIa(t)lUti< A2(T) + Bx)|I»(t)|C,0.Til»(x•t)|lв2, • где A,(T) = ||«xXL2(0,1) + T|k(x)|L+ ^If(x.t)x|t2(Dt) + 2|     x)|      ' ^^<4’(x)|„,„ '

2 ,        O2

⁺ _a     l ^f " ⁽ x ' t 'II L 2 ( D T ) ’ A ^{2( T} ) =1 I h ⁽ t 'I С [ 0. T ]{l I ^{6 (} t ) - ^{f (0-} t )l C [ 0. T ] ⁺ ^1 ' f x ⁽ x ' t ) C Ю- T 11 I L .«Щ ⁺

+ O1?!x)^(07) + ^(x)L=<« + 0760     (x'tD)B1(T) = T2 +

^B 2 ^{( T} ) = 1 ⁶ "¹⁽ t 1™ T 1 ⁽ 7^ ^{T +} 76 }

Из неравенств (27), (28) заключаем:

II»(x• t)|B-t +1»(t)|C|a,]s A(T) + B T >1 a(t)|C|o.т]ll»(x• t)|B2,. ■ где A(T) = A,(T) + A2(T), B(T) = B1(T) + B2(T).

Итак, можно доказать следующую теорему.

Теорема 1 . Пусть выполнены условия 1-4 и

(A (T) + 2)2 B (T) < 1.(30)

Тогда задача (1), (2), (2), (6) имеет в шаре K = KR(||z||£s < R = A(T) + 2) пространства Е-, единственное решение.

Доказательство. В пространстве Е, рассмотрим уравнение z = Ф z,(31)

где z = { и , a } , компоненты Ф i ( и , a )( i = 1,2) оператора Ф ( и , a ) определены правыми частями уравнений (20) и (23).

Рассмотрим оператор Ф ( и , a ) в шаре K = K R из Е: 5 . Аналогично (29) получаем, что для любых z , z 1 , z ₂ 6 K R справедливы оценки:

II ^Ф z |I e_T <  A ( ^T ) + ^B ( ^T )| a ( t )| C [0, T ] 11 » ( x • t )| B 5 _T .                                 (32)

II ^фч - Ф *' 2 1 I E S <  B ( T ) R (| B 1 ( t ) - a 2 ( t ) C _{[ 0} , _{T ]} +1 » , ( x , t ) - и 2 ( x , t ) B 2 _T ) .               (33)

Тогда, из оценок (32), (33) с учетом (30) следует, что оператор Ф действует в шаре K = K_R и является сжимающим. Поэтому в шаре K = K R оператор Ф имеет единственную неподвижную точку { » , a }, которая является в шаре K = K R единственным решением уравнения (31), т.е { и , a } является в шаре K = K R единственным решением системы (20), (23).

Функция и ( x , t ), как элемент пространства B^:5_Т , имеет непрерывные производные

и ( x , t ), »_x ( x , t ), u_xx ( x , t ), u_xxx ( x , t ), u_xxxx ( x , t ) в D_T .

Из (8) нетрудно видеть, что

1                         1

(                            2     1 (                            2     1

Е ^{( Я} к II » k ⁽ t )| 1 c [0, Т 1 )      <- Е ⁽ ^ k ll » k ⁽ t )| C [0, Т 1 )      ⁺“ l ^f x ⁽ x , t ) ⁺ a ⁽ t ) » x ⁽ x , t )l I c [0, T limn

V k = 1                      V      ^a V k = 1                      V ^a                                  "L 2 ^(U,1)

Отсюда следует, что » tt ( x , t ), »_ttxx ( x , t ) непрерывны в D_T .

Легко проверить, что уравнение (1) и условия (2), (2) и (6) удовлетворяются в обычном смысле.

Следовательно,{ u ( x , t ), a ( t )} является ^ешением задачи (1), (2), (5), (6), п^ичем в силу леммы 2 оно единственное в шаре K = K R . Теорема доказана.

С помощью леммы 1 доказывается следующая

Теорема 2. Пусть выполняются все условия тео^емы 1 и

J р (x ) dx = 0, J у (x ) dx = 0, J f ( x , t ) dx = 0(0 <  t <  T ), ^ (0) = h (0), ^ (0) = h ‘ (0).

Тогда задача (1)-(4) имеет в шаре K = K R (|| z||_£ s <  R = A ( T ) + 2) из E T единственное классическое ^ешение .