Обратная спектральная задача для оператора Лапласа и ее приближенное решение

Пусть

П = {ж = (x₁,x₂,...,xn) : 0 < яг, <  aj,j = 1,...^}) «J > 0.

В пространстве ^(П) рассмотрим дискретный самосопряженный оператор То, определенный краевой задачей Дирихле

-Ан = Ад, фп = 0,                           (1)

где А — оператор Лапласа, 5П — граница П.

В настоящей работе исследуется обратная задача для степени оператора То, порожденного краевой задачей (1). Основным методом исследования является так называемый резольвентный метод, теоретически обоснованный в работах [1, 2]. Применяя идеи этого метода, мы доказываем теоремы существования решения поставленной обратной задачи. Впервые рассматривается случай, когда оператор Лапласа имеет непростой спектр. В работе также описывается процедура численного нахождения приближенного решения.

Отметим, что обратные спектральные задачи в различных постановках играют фундаментальную роль в различных разделах математики и имеют множество приложений в естествознании. Большинство работ в этом направлении связаны с обыкновенными дифференциальными операторами. Что касается операторов в частных производных, то здесь, в основном, рассматривается степень оператора Лапласа с простым спектром. Так, в работах [1 - 6] решена обратная задача для степени оператора Лапласа больше 2 на прямоугольнике. В работах [7 - 8] поставленная задача решена для степени больше 3/2, в работах [9 -10]- для степени больше единицы. Обратная задача для оператора Лапласа с кратным спектром раннее не исследовалась.

1.    Постановка обратной задачи

Р00

Рассмотрим оператор Т = I X^dE(X), являющийся степенью оператора То, где Е(Х) Jo

— спектральное разложение единицы оператора То, /3 > 1, А^ > 0 при А > 0.

Очевидно, спектр а(Т) оператора Т неоднократный. Иногда, для удобства будем нумеровать упорядоченные по возрастанию собственные числа X_m = \mi,m2,...,m_N) оператора Т и связанные с ними спектральные объекты одним нижним натуральным индексом и одним верхним, при этом верхний индекс будет отвечать за кратность щ собственного числа Xt, т.е. Xt = А^ = Х{, к = 1, г^.

Пусть Р — оператор умножения на вещественную функцию р G ^(П), называемую потенциалом.

Обозначим через pt собственные числа оператора Т + Р, занумерованные в порядке возрастания действительных частей с учетом алгебраической кратности, а через щ — соответствующие им ортонормированные в ДгСП) собственные функции.

Рассмотрим следующую обратную задачу спектрального анализа.

Пусть дана последовательностью комплексных чисел {(i}“i, близкая к спектру оператора Т. При различных степенях /3 > 1 требуется доказать существование оператора Р, такого что спектр а(Т + Р) совпадает с последовательностью {^}“_?

2.    Основные спектральные тождества

Сформулируем вспомогательные утверждения, на которых базируется доказательства основных результатов данной статьи. Доказательства самих вспомогательных утверждений приведены в работе [И].

Обозначим:

Д₀(А) = (Т-АР)"¹, Д(А) = (Т + Р- ХЕ)-¹;

щ = {А : Re А = ^-^}, Г₍ = {A G С : Ы б a_t}, _7f = {A G С : |А* - А| = г₀},

П = - min{At+i - At; At - At-i}, r0 = inf rt;

Qt = {A : |А* - A| > ro}, Q=A^, ^ = TT «J

Лемма 1.

Если ||P|| <  r/2, где 0 < r < го, то оператор T + P — дискретен, причем

• (г) если Ro(X) Е &_q, mo R(X) E &_q, 1 < q < oo,

• (ii)    если At G C \ Qt, mo pf E C\^t, s = 1,щ, vt—кратностъ собственного числа X/.

Теорема 1. Если /3 > N/2, \\Р\\ < г/2, где 0 < г < го, то для любого t Е N имеет место спектральное тождество:

22 № = ^t - £(^t^S)^t^S)) + ^at(p\                 (²)

S=1              S=1

где at(p) =

в/„ “p [вд(^(Ч)^!

dX.

3. Степень оператора Лапласа с потенциалом на N-мерном параллелепипеде

В данном разделе доказывается теорема существования решения обратной спектральной задачи для оператора Лапласа на многомерном параллелепипеде. Приводятся условия, налагаемые на произвольную последовательность, при соблюдении которых спектр возмущенного оператора будет совпадать с данной последовательностью.

Лемма 2.

37V            °°_л

Если (3 > ——, то ряд / r^ шах 11^0(^)112 сходится.

ОО

Если (3 > N, то ряд rt max ||Яо(А)||² сходится.

Обозначим сумму первого ряда через s², а второго через Soq.

Основные результаты данного раздела выражают следующие утверждения.

Теорема 2. Пусть /3

ЗА                 г 1 н ,

—, г G (О,тт{го,—п=}). Если для комплексной

последовательности {^} выполняется неравенство:

ОО l>t

t=i к=1

2 г

< 2

где ш = V^sr < 1, то существует потенциал р 6 ^(Щ такой, что для любого i G N

ft

V

k=l k=l

гдеа(Т + Р) = {^}.

Теорема 3. Пусть (3 > N, г < min{ro, — w = 2^N s^r. Если для комплексной ^00-2

последовательности {^} выполняется неравенство:

ОО ft

2^ W

г

t=l k=l то существует потенциал p 6 ^^(П), такой, что для любого i € N выполняется ft          f

k=l k=l

гдеа(Т + Р) = {^}.

Введем в рассмотрение следующую систему функций:

N

фт(х} =

3=1

2TrmjXj аз

где т = (т\,... ,m^),mj G {0} UN, q - число ненулевых индексов в мультииндексе т. При n»j G N эту систему будем нумеровать нижним и верхним индексами так же, как и систему {v_m}, т.е. в соответствии с нумерацией собственных чисел А*.

Лемма 3. Множества М вещественных функций р G £₂(П), обладающих следующими свойствами:

p(ai - xi,X2, ■ ■ ■ ,x^)=p(xi,a2 — х2,... ,х^) = .. .=p(xi,x2,... ,а^ — хм) =

= р(х\,х₂,... ,xn) для почти всех (xi,x₂,... ,xn) G П, (5)

N

(p, Рт) = о, при JJ m₇ = 0, m, = 0,1,...,                      (6)

j=i

I|PIU2 <                                               (7)

замкнуто в L2(H).

Лемма 4. Если ||Pj|| < г/2, 0 < г < Tq, j = 1,2, то l«t(pi) - а*(рг)| < rrt\\Pi - P2|| max ||йо(А)||2.

Лете

Перейдем к доказательству теоремы 2.

Доказательство. В пространстве 12(П) рассмотрим уравнение относительно р:

р = а0- а(р),(8)

где

ОО

«о = (-1)^^^Й - Xt)pkt,(9)

i=l fc=l

^Р) =(10)

t=l fc=l *

Из вида уравнения следует, что решение удовлетворяет свойствам (5) и (6).

Введем оператор А : 1₂(П) —> £г(П), определяемый равенством: Ар = ао~ <Др).

Так как ||Ap||i₂< ||ао|| + ||а(р)|| < ^(1 - ш) + ^ш = ^, то оператор А отображает замкнутый шар Я(0, g) в себя. Можно показать, что пересечение данного шара с множеством функций, удовлетворяющих свойствам (5) и (б), замкнутое множество. Используя лемму (4) покажем, что оператор А сжимающий в этом подпространстве.

\\А_Р1 - Ap₂\\_L2 = На^) - а(р₂)|| = ^[2ДV Н±^МР\ <

\ы ы Vi / v^r||pi -p2||b2s = w||pi — P2||i2-

По принципу С.Банаха уравнение (8) имеет единственное решение р.

Определим оператор Р, действующий в 1₂(П), следующим образом: Pv(x) = р(х)и(х), где р — решение уравнения (8). Оператор Т + Р дискретный, и его собственные числа ц_т также можно занумеровать одним нижним и одним верхним индексами. Покажем, что решение р и есть искомый потенциал.

Умножим скалярно уравнение (8) на функции ip^ и просуммируем по k = 1, щ- Получим

^(р,^) = (-i^vW^e*    - (-1)^«₍(р).        (п)

к=1                      к=1

Используя свойства (5)-(6), преобразуем

{PVm,Vm) = NT Р(^Х^ ■ • • I I ^sm --- )^dx^ • • ‘ ^dxN =

• ^{v                        V а}з ⁷

4.    Возмущенный оператор Лапласа с неядерной резольвентой на TV-мерном параллелепипеде

_v j_nP^-                   •^{dXN =} ypv ^p’'

Отсюда, учитывая кратность k=l                 И к=1

Подставляя (11) в (12) и сравнивая с (2), получаем (3).                              □

Замечание 1. Оператор Т + Р, обладающий свойством (3), неединственен.

Действительно, достаточно поменять местами два члена последовательности {^К=1, попадающих в одну сумму ^ |^ — АД2, и мы получим другую последовательность {Ct }^i-fc=i

Объединим в один класс Р все операторы, спектр которых обладает свойством (3). Если мы не будем различать представителей этого класса, то можем говорить о единственности решения обратной задачи.

Как уже говорилось во введении, чаще всего в обратных задачах рассматривается степень оператора Лапласа, так как в данном случае мы будем иметь ядерную резольвенту. Но в приложениях более важную роль играет сам оператор Лапласа, а не его степени. С помощью специально подобранных аналитических функций в работе[12] удалось получить результат для оператора Лапласа с простым спектром, но формулировался он не для самих собственных чисел, а для значений введенных функций, зависящих от собственных чисел. В данной работе полученный результат обобщен на случай кратного спектра.

Пусть функции /t : С —> С таковы, что ft(X_n) = §t_n, где $tn — символ Кронекера и пусть

Pt = sup (IА|² • |/t(A)D < ОО. Введем функции ^(А) = / ft(z)dz.

ReA>0                                           JO

Можно показать, что функции

=           П*1

ОО п k=l,k^t

Afc-A А*; + А

, ReA > О,

где нормирующие множители At выбраны из условия ft(Xt) = 1, £ € N удовлетворяют указанным выше условиям.

Теорема 4. Если для комплексной последовательности {(^} существует подпоследовательность {ct} С {at} такая, что выполняются следующие неравенства:

00 Л

• (i)    ш = 2^4 max ||й₀(А)||2 ^ - < 1,

  

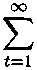
  52 52 (9^) - д^)}

  Aj <с% fc⁼l

  
  
5.    Степень оператора Лапласа с потенциалом на равнобедренном прямоугольном треугольнике

Г°/1 А yfl-w), то существует потенциал р, такой, что для любого t € N

Е EX = Е EX).

\j ^—1             Aj

Доказательство этой теоремы основывается на тех же идеях, что и теорема(2)

В данном разделе впервые рассматривается непрямоугольная область.

Пусть К = {(х,у) ■ 0 < х < у <  7г}. В пространстве L^K) рассмотрим дискретный самосопряженный полуограниченный снизу оператор То, порожденный краевой задачей Дирихле (1).

Введем оператор Т = $^ X^dE(X), где Е(Х) — спектральное разложение единицы, ^ > 1, А^ > О при А > 0.

Нетрудно показать, что собственным числам Х_тп = {т² + п²)^ оператора Т соответствуют собственные функции v_mn = ^/^(sin тх sin пу — sin пх sin ту), т > п > 0, образующие ортонормированный базис в L^K).

Положим:

Фа               Sm>n>o5jfcO (^^(m+nj^tm-n) шах ||J?o(A)||2   +

4             ^^(m+Xbn-n)

тах №(А)||2);

АеТ2Н1т,2Н1„         '

2)0<г‘<1,,ыЫ^4

• 3)    фтп = ^ (cos тх cos пу + cos пх cos ту), т,п = 0,1,....

Теорема 5. Пусть ^  >  2, г Е (0, min{ro,—7=—}). Если для комплексной

ЗуЗвд последовательности {^_тп} выполняется неравенство:

4 I °° 1

j 5 2 I 52 2^^ (Ф(т+п),2^А(т-п) ^2^1е (т+п),2^к (т—п))

т>п>0 fc=0

Е (я--^-)= £ (и-^,.-.

(4.1)

m2+n2=Xt                     m2+n2—Xt где а(Т + Р) = {ртп}.

6.    Численные расчеты

В этом разделе описывается процедура получения приближенного решения обратной спектральной задачи. Для этого используется основное уравнение, приведенное в процессе доказательства теоремы (2) существования решения обратной задачи. Для простоты ограничимся изложением двумерного случая.

Поставим задачу найти приближенное решение, существование которого показано в теореме (2).

Введем в рассмотрение следующую систему функций:

. .    4 2тгтх 2тту

Ртп(х) = -7=7 ^cos----- ^cos —I—-Vab a b

При m,n > 0 эту систему будем нумеровать нижним и верхним индексами в соответствии с нумерацией собственных чисел А*.

Уравнение р = ао — а(р), где

ОО Vt                                         ОО Vt     , у t=l k-1                        t=l Ы   t

<ЭД =    / ASp[P(A)(PP0(A))2]dA = ± [

oo

А8р[^йо(А)(Рйо(А))^А, k=2

имеет единственное решение р.

Найти его можно методом последовательных приближений.

Пусть р₀ = 0, тогда p_t+i = «о - Mpt), ltoi-юой = Р-

Найдем приближенное решение р.

р = а₀- 5(а₀), где

здесь aj — к-тая поправка теории возмущении:

а^^'!^^ А8р[йо(А)(Рйо(А))‘] ^{dX =} ^r/_y ^SpAA(A)]^A.

Оценим разности к-х поправок, к >2.

laf’W-afti)! =

2^ ^ Sp [№(А))‘ - (АЯо(А))¹] dX

^пш|(РДо(А))к - (Р12?0(А))*||1 < max V(PiP0(A))s(P - POPoUXPPotA))*-5-1

у max ( £ ||Р - Pill ||Яо(А)|Ц ||йо(А)||М I

\s=0                                       /

MP-ЛИ (^Мпш(||Ло(А)||2||йо(А)||м).

Здесь Pi— оператор умножения на pi, т.е. на «о- Далее оценим модуль разности:

ОО / \ k

|«i(p) - «ЭД)| < MP - АН J max ||Ро(А)||2 ^ k) max ||P₀(A)||^fc< 2 *G7t         гк ^2/ Лец

«=0

rrdlP-ftllmaxHJWAJg <гг,(||Л + ||Л||)?ш||ВДЙ < ^S max || Ло (А) ||®.

Ae7t                            леи             у/ab леи

Итак,

Ыр) -ас(ао)| < ^тах||йо(А)||2. yob ^t

“t(ao) = i / А8р[Ло(А)(АЯо(А))2]^ =

₌ у д (pw^v^^    - V V !^М!!

j&k^i ^л* ^Аз        3&к=1 V

Таким образом, р = а₀- V^£_t&^tl^ ^-^l ^'

На основе полученного результата в среде Maple 6 впервые создан программный продукт, позволяющий численно находить приближенное решение поставленной обратной задачи.

Положим для примера а = 1, b = ^3, /3 = 5/2, £_тп = А_тп + 0.0001. Тогда приближенное решение, вычисленное по первым четырем членам последовательности {^_mn} имеет вид:

р = 0.3999996438соз(25.13274123ж)соз(9.548376831у) + 0.4006108966+

+0.3996028571^(4.774188417;/) + 0.3999774004соз(9.548376831у)+

+0.3999955835cos(14.32256525y) + 0.3998713899соз(6.283185308ж)+

+0.3999953594соз(19.09675367у) + 0.3999939656соз(6.283185308ж)соз(9.548376831у)+

+0.3999665522cos(6.283185308s)cos(4.774188417y)+

+0.3999990308соз(6.283185308ж)соз(19.09675367у)+

+0.3999987184соз(6.283185308ж)соз(14.32256525у) + 0.3999958620соз(12.56637062ж)+

+0.4000013739соз(12.56637062ж)соз(14.32256525у)+

+0.3999970936соз(12.56637062ж)соз(9.548376831у)+

+0.3999958348соз(12.56637062ж)соз(4.774188417у)+

+0.4000019328соз(18.84955592ж) + 0.3999996560соз(12.56637062ж)соз(19.09675367у)+

+0.3999997128соз(18.84955592ж)соз(14.32256525у)+

+0.3999993495соз(18.84955592ж)соз(9.548376831у)+

+0.3999984754соз(18.84955592ж)соз(4.774188417у)+

+0.3999999510соз(18.84955592ж)соз(19.09675367у)+

+0.3999999768соз(25.13274123ж) + 0.3999999242соз(25.13274123ж)соз(19.09675367у)+

+0.3999998700cos(25.13274123a;)cos(14.32256525y)+

+0.3999995842соз(25.13274123ж)соз(4.774188417у).