Обратная задача для нелинейного интегро-дифференциального уравнения с гиперболическим оператором высокой степени

Представляют большой интерес с точки зрения физических приложений обратные задачи для

.                                                    -

,                                                    ,

.

-

-

.

,

,XVIII

.                                                                                        ,- нений в частных производных первого порядка представляют собой производную неизвестной

.                                                   ,,

,

.

В области D = DT х R рассматривается нелинейное уравнение вида d2 jd_)n d t2 dx 2 ,

( T ~

u ( t , x ) = f t , x ,J J K ( s , y ) u ( s , y ) dyds , ^ ( t )

V с начальными условиями d i                                            __________

u(t,x)t=0 = Фх (x), ——U(t,x)|t=0 = Ф^+1(x), xe R , i = 1,2n—1 1d 1

и дополнительными условиями

u(t,x)ю_ж = У (t), te Dt, x=x 0

#( t )| t=0 = Ф 0 = const, где u(t,x)   и ^(t) - неизвестные функции, f (t,x,u,^)e C(DхRхDT), фi(x)e C(R),

___                    t ~ i = 1,2n, у (t)e C(DT), 0 < J J K(s,y)dyds, DT =[ 0,T ], 0 < T <^ , n - произвольное нату-0 —^

.

,                                                                                                                                                                                      - кально решаются методами теории обыкновенных дифференциальных уравнений при помощи

.                                                                                                                    -

Математика

ность описания явлений при помощи волн и при помощи частиц. Применение метода характеристик к решению дифференциальных уравнений в частных производных первого порядка позво-ляет свести изучение эволюции волн к изучению распространения частиц [1]. В работах [2-4] разработана методика для интегрирования нелинейных уравнений в частных производных перво -го порядка. По сути, данная методика ближе к методу характеристик и её авторы называли методом дополнительного аргумента.

В настоящей работе изучается обратная задача, где восстанавливаемая функция ^ ( t ) нелинейно входит в уравнение. При решении обратной задачи (1)-(4) относительно восстанавливаемой функции получается нелинейное интегральное уравнение Вольтерра первого рода, которое с помощью неклассического интегрального преобразования сводится к нелинейному интегрально -му уравнению второго рода. Задание условия (4) при преобразовании обеспечивает единственность решения нелинейного интегрального уравнения первого рода и определяет значение неиз -вестной функции в начальной точке t = 0, т.е. 9 (0) = ф₀ . Обратные задачи для нелинейных дифференциальных уравнений в частных производных ранее рассматривались в работах [5, 6].

Определение. Решением обратной задачи (1)-(4) называется пара непрерывных функций {u ( t , x )е C ² n ^,2 n ( D ), ^ ( t )е C ( DT )} , удовлетворяющая уравнению (1) иусловиям (2)-(4).

• 2.    Задача Коши (1),(2)

Левую часть уравнения (1) запишем в виде

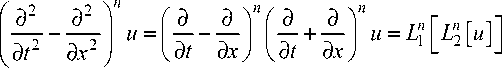
где ^L \l₂ [ u ]l —^{( L}2 [ u ]) t ^{( L}2 [ ^u ]) x , ^L 2 [ ^u ] ^— u t ⁺ u x .

Тогда уравнение (1) приобретает вид

(    t ”                       k

L n [ L n [ u ]] = f t , x , jj K ( s , y ) u ( s , y ) dydsXt ) .

k     0 -~                        7

Из (5) видно, что уравнение (1) имеет две n -кратные характеристики: 1) x - t = C 1; 2)

x +t = C2, где Q, C2 - произвольные постоянные. Тогда, интегрируя уравнения (5) n раз вдоль линии второй характеристики, получаем

^{L 1} [ ^L 2 ^{[ u ]}] =

Ф 1 ( x + t ) + j f

( T ~ s,x, j j k 0 ^

K(9, y ) u(9, y ) dyd9,P(s ) ds ,

L n ^-2 [ L n [ u ]] = Ф₂ ( x + t ) + Ф 1 ( x + t ) t + j ( t - s ) f

T ~                          k s, x, j j K(9, y)u(9,y)dyd9,P(s) ds,

0 -~                        7

n                   ^n - i

^L n ^[ u ^]= i = 1 ^ф , ( x + . ) —+

Г ( t - s ) n ^{-1 j} ( n -1)!

T ~                          k j j K(9,y)u(9,y)dyd9,P(s) ds,

0 -~                         7

где Ф i (i = 1, n) - произвольные непрерывные функции на действительной оси, которые подлежат определению.

Из (6), в силу начального условия (2), имеем Ф1(x) = ф2n. Так как вдоль линии второй харак теристики dLn2 [ u ]   dLn [ u ] dLn2 [ u ] dx

= ( L n [ u ]) _t -( L n [ u ]) x ,

dt d t dx d t dnL2 [u ] _( d d k n„, L') I u dtn     k d t dx 7

Юлдашев Т.К.        Обратная задача для нелинейного -нтегро-дифференциального уравнения с гиперболическим оператором высокой степени то, в силу условия (2) из (7), (8) имеем

^Ф 2 ⁽ x ) = V 2 n - 1 ⁽ x Х-,^Ф n ⁽ x ) = V n + 1 ⁽ x X

Тогда уравнение (8) приобретает следующий вид:

n                   t - 1

L n [ u ]=Ё V n + i ^{( x +} t ) ( j -^⁺

t

J

( t - s ) n ^-1 ( n -1)!

T ~                        I s, x, J J K(0, y)u (0, y)dyd0,0(s) ds, о -~                         7

где x - играет роль параметра.

Аналогично, интегрируя интегро-дифференциального уравнения (10) n раз вдоль линии первой характеристики, получаем nt

L 2 ^-1 [ u ]=^ф n + 1 ( x - t )+у J V n + j ( x + s ) j = 10

+fc s ) n

J 771

0 n ^!

T ~

$ j ^-1

—---ds +

( j -1)!

р- f s , X ,J J K ( 0 , y ) U ( 0 , y ) dyd0,0(s ) ds , V     о -~                         7

n t                            _s^j - 1

L2-2 [u ] = фn+2 (x - t) + фn+1 (x - t ) t + У J (t - s)Vn+j (x + s )       ds + j=10                      (j 1)!

f ( t - s ) n ⁺¹

^J₀ ( n +1)!

T ~                          A

J J K ( 0 , y ) u ( 0 , y ) dyd0 , 0 ( s ) ds , 0 -~                         7

2 n                   ,2 n - i       n t          n - 1                     „j - 1

u ( t , x ) = у Ф ( x - 1 ) -I ----+y [2 1 -^2— V ( x + 1 )_2--- ds +

, ' i ^У .1 ^A      (2 n - i )! £J ( n -1)! ^ ^{n +} j'     У j -1)!

t

J

⁽ t ^{- s} )

2 n - 1

t ~

(2 n -1)

- f s , x ,J J K ( 0 , y ) u ( 0 , y ) dyd0,0(s ) ds , ^! V 0 -~                            7

где Ф _i ( i = n +1,2 n ) - произвольные непрерывные функции на действительной оси, которые подлежат определению.

Из (11) в силу начального условия (2) имеем Ф n+1(x) = vn • Так как вдоль линии второй характеристики справедливо (9) и вдоль линии первой характеристики du  дu  дu дx              dnu

=--1---= ut + uv, ••• , ----- dt   дt   дx дt                 dtn

д д u,                        (14)

1 д t дx то в силу (2) из (12) и (13) следует, что

^Ф n + 2 ^{( x} ) = V n - 1 ^{( x} Х-,^Ф 2 n ^{( x} ) = V1 ^{( x} )•

Итак, из задачи Коши (1), (2) мы пришли к следующему нелинейному интегральному уравнению :

n                 t^ - 1

u ( t , x ) = 0 1 ( t , x ; u ,0) = У V_i( x - 1 )

nt

+П

⁽ t ^{- s} )

n - 1

( n -1)

- V n + j ^{( x +} t )

5 j ^-1

—---ds +

( j -1)!

t          2 n - 1

j ( £ z s )___ J (2 n -1)!

(       t ”                                        I f s,x,J J K(0,y)u(0,y)dyd0,0(s) ds,

V     0 -~                         7

где x - играет роль пapaмeтpa•

В (15) отметим, что функции V i( x - 1 ), V ₂( x - 1 ),•••, V_n ( x - 1 ) являются первыми интегралами

_ o (д^дan уравнения I —I--I u = 0 и они постоянны вдоль решения этого ypaвнeния• Производные этих V д t дx 7

функций вдоль первой характеристики равны нулю и сами эти функции удовлетворяют данному уравнению •

Математика

А функции фп+1(x +t),фп+2(x +t\..,,Фтn(x +1) являются первыми интегралами уравнения d t

д) n дx 7

и = 0 и они постоянны вдоль решения этого уравнения. Вдоль второй характеристики

эти функции удовлетворяют данному уравнению. Исходя из этих соображений, покажем, что интегральное уравнение (15) удовлетворяет дифференциальному уравнению в частных производных (1). Путем 2п -кратного дифференцирования вдоль линий соответствующих характеристик из (15) получаем следующее дифференциальное уравнение d 2 nu dt2 n

(     T ~                        7

= f t , x , j j K ( s , y ) и ( s , y ) dyds X t ) .

k     о -~                        7

Так как вдоль линии второй характеристики справедливо (9) и вдоль линии первой характеристики - (14), то имеем для левой части (16)

d ² n u dt²""

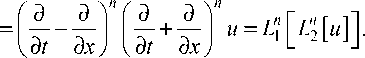
Отсюда заключаем, что из (16) следует дифференциальное уравнение в частных производных (1).

Используя условие (3), из интегрального уравнения (15) получаем

A t ^-1    ^г( t - s ) n ^-1

^ t ⁾=£ ^{ф (}* ^- t '.⁺§ h n -i>r

_s ^{j -1}

Ф п + j ^{( x} 0 ⁺ t )        ds ⁺

⁽ j ^{- 1)!}

или

f ( t - s )² n ^{-1 j} (2 n- 1)!

T ~                          7

s , x ₀, j j K(9,y ) и(9,y ) dyd9,9(s ) ds о -~                        7

t j h

t , s , j j K ( 9 , y ) и ( 9 , y ) dyd9,9(s ) ds = g ( t ), о -~                        7

где g(t) = ф(t)- ^ф-(xо -t)-t    -^j(t s)   Фп+j(xо + t)-s—— ds, i=1               (1 1)! j=1 о (n 1)!                     (j 1)!

7 T “                             7

h t , s , j j K ( 9 , y ) и ( 9 , y ) dyd9 , ^ ( s ) =

= ( t - s )^{2 n -1} = (2 n - 1)!

о -^

7     T ~7

f s , x о , j j K ( 9 , y ) и ( 9 , y ) dyd9,9(s ) .

k     о -~7

Относительно восстанавливаемой функции ^ ( t ) уравнение (17) является нелинейным инте

гральным уравнением Вольтерра первого рода. Его с помощью классических методов невозможно свести к интегральному уравнению Вольтерра второго рода, к которому мы могли бы применять метод последовательных приближений. Уравнение (17) запишем в виде

9( t ) + j n ( s ) ^ ( s ) ds = 9( t ) + g ( t ) + j о                                    о

G ( s ) ^ ( s ) - h

7    t ~                        7

t , s , j j K ( 9 , y ) и ( 9 , y ) dyd9,^,^s )

k    о -~                         7

ds ,

t

о <  G ( t ) - произвольная функция такая, что

exp <

•«1.

I о

Применяя к (18) метод резольвенты ядра [-G(s)], получаем z7( t) = h (t) - j G (s) exp (-д( t, s)) • h (s) ds,                            (19)

о

Юлдашев Т.К.

t где h (t) = 0( t) + g (t) + j

G ( s ) 0 ( s ) - h

Г   T ~                        A t, s, j j K(0, y)и (0, y)dyd0,0(s)

A  0 ~                    7

ds ,

M( t , s ) = j G ( 0 ) d0 , ^ ( t ,0) = д ( t ). s

Применяя к (19) формулу Дирихле, получаем

0 ( t ) = 0₂( t ; и , 0 ) = { 0 ( t ) + g ( t ) +

t

+1

G ( s ) 0 ( s ) - h

Г   t ~                        a t,s, j j K(0,y)и(0,y)dyd0,0(s)

A    0 -~                         7

ds > exp (- ^ ( t )) +

t

⁺j G ⁽ s ) exp (- д ( t , s )){ g ⁽ t ) - g ⁽ s )+ ^{0 (} t ) - ^{0 (} s )+

t

+1

s

-1

G ( s ) 0 ( s ) - h

G ( 0 ) 0 ( 0 ) - h

Г   t ~                        a t,s, j j K(0,y)и(0,y)dyd0,0(s)

A    0 -~                         7

ds

-

Г    T ~                         A s,0, j j K(Z, y)и(Z, y)dydZ,0(0)

A     0 -~                          7

70 ; ds .

Уравнение (17) при начальном условии (4) эквивалентно уравнению (20).

• 4.    Разрешимость обратной задачи (1)-(4)

Итак, мы получаем, что разрешимость обратной задачи (1)-(4) эквивалентна разрешимости следующей системы нелинейных интегральных уравнений:

и ( t , x ) =© 1 ( t , x ; и , 0 ),

0 ( t ) _s© 2 ( t ; и , 0 ).                                       ⁽⁾

Для произвольной непрерывной в области D функции h (t, x) норму вводим следующим об разом : ||h(t,x)|| = max |h(t,x)|. Аналогично вводится норма для функции одной переменной в об-

( t , x ) e D

ласти D_T .

Теорема. Пусть выполняются следующие условия:

I V i ⁽x )| ^ M i ^,0< iLM* T 1)! - ^A 0 <"^;

f ( t , x , и , 0 ) e Bnd ( M 0 ( t )) n Lip { L 0 ( t )| _ц , 7 1 ( t ) |0 };

^T (T — s ) 2 n - 1

⁰ <1 n ---nT M 0^{( s} ) ^{ds -A} 1 <"^;

0 ^{(2 n -1)!}

^T (T - s ) 2 n - 1

⁰< I И ---nT L 0 ^{( s} ) ^{ds - A} 2 < ^^;

0 ⁽² n ^{- 1)!}

^T (T - v^2 n - 1

⁰ <1 O ---nT L 1 ^{( s} ) ^{ds -A} 3 <^^;

0 ^{(2 n -1)!}

P< 1, гдe p = тах{ Д 1 ; Д 2 }, A = тах{А з ;A 3 M 0 }, P1

r.                       )..

= max 2; 1+ J G ( t ) dt + а А₂ M ₀ >,

I A 0                   7

t ~ а = jj ||K(t,x)||dxdt, M0

0 -^

= max <  t

exp(- ^ ( t )) + 2j G ( s )exp(- ^ ( t , s )) ds >«1. 0                                        ,

Математика

Тогда обратная задача

(1)-(4)

имеет единственное решение

{ u ( t , x ) e C ² n ^,2 n ( D ), Н ( t ) e C ( D_r )}.

Доказательство. Используем метод последовательных приближений. Рассмотрим следующий итерационный процесс:

J u 0 ( t , x ) = 0, Н 0 ( t , x ) = 0, u k + 1 ( t , x ) = 0 1 ( t , x ; u k A )

U ₊ 1 ( t , x ) e0 ₂( t ; u k A ), k = 0,1,2,...             ’

Тогда в силу условий теоремы из (22) получаем, что справедливы следующие оценки:

2 n

II ^u 1 ⁽ t , x )^- и 0 ⁽ t , x ⁾|| < £ M i

i = 1

t

II ^u k + 1 ⁽ t , ^x )^{- u} k ⁽ t , ^x )ll < f

T - 1      t ( t - s ) 2 n - 1

⁺f щ—nT ^M 0 ^{( s} ) ^ds <^A 0 ^+A 1 ^;

⁽ I ^-1)! 0 ^{(2 n -1)!}

⁽(-_{2 n} ^s - ₁)_! ( L 0 ( ^s )l u k ^{( s} , ^x ) ^{- u} k - 1

⁺ L1 ( ^s )| Н ^{( s} ) ^- ^ k - 1 ^{( s} )|I) ds < ^A 2 I u kk ⁽ t , x )

-

^u k - 1

⁽ t , x )||^+A3| H ⁽ t ) - ^H k - i ⁽ t )l|;

;

||^H 1 ⁽ t )^{- H} 0 ⁽ t )|| < || g ⁽ t )|| ⁺ J|| h ^{( t,s ,0,0)}|| ^{ds ex}P(^- A ⁽ t )) ⁺ V 0               7

)            (..                                                    )

+2f G ( s )exp(- ц ( t , s )) || g ( t )|| + f| h( ( t,s ,0,0)|| ds ds < || g ( t )|| + f|| h ( t,s ,0,0)|| ds M,

0 ,

M 0 = max <  t

exp (- ^ ( t )) + 2f G ( s )exp (- ^ ( t , s )) ds >«1, 0                                        ,

t

|| H k + 1 ( t ) - H k ( t )|| < h + fl G ( s )|| ds +

J ( t z s )^ n :i ^f (2 n -1)!

T _M

^L 0 ( s ) f f K ( ^ , У )ll dyd^ds f M 0I| u k ( t , x )

^{- u} k - 1 ⁽ t , ^x )||⁺

t

+f

0 -^                    ,

( t - s )^{2 n -1}

L1 ( s ) dsM 0 U k ⁽ t )- ^H k - 1 ⁽ t ) < (2 n -1)!

(    T                 )

< 1+ J G ( t ) dt +aA ₂ M ₀ u k ( t , x )

I    0               )

^^^^^^^s

^u k - 1 ⁽ t , ^x )|| ^{+ А} 3 M 0 || ^H k ⁽ t ) ^{- H} k - 1 ⁽ t )||,

t ~ где a = f f ||K(s, y)||dyds.

0 ^

Примем обозначения

J ( T                  ^    ]

P1= max2; 1 + f| G ( t )|| dt + aA ₂ M ₀ >

, в = тах{А з ;A 3 M 0 }, p = max{ ^ i ;A).

IV 0                   7

Тогда из (24) и (26) имеем

|| Uk+1( t,x)- Uk(t,x )|| < pUk(t,x)- Uk-1( t,x)||, где ||Uk(t,x)- Uk-1(t,x)|| = Iuk(t,x)- uk-1(t,x)||+1|Hk(t)- Hk-1(t)||.

Из оценок (23), (25) и (27) следует, что операторы в правой части системы (21) являются сжимающими и, следовательно, обратная задача (1)-(4) имеет единственное решение { u ( t , x ) e C ² n , ² n ( D ), Н ( t ) e C ( D T )}.

Юлдашев Т.К.        Обратная задача для нелинейного -нтегро-дифференциального уравнения с гиперболическим оператором высокой степени