Обратная задача в управлении динамической системой

Задача наведения характеристической точки рабочего инструмента манипуляционного робота (МР) при выполнении им различных работ промышленного и непромышленного характера является одной из основных. Трудности при синтезе законов управления такими многомерными, нестационарными объектами определяются их нелинейными свойствами, обусловленными кинематическими и динамическими связями [1 – 3].

В работе прямым методом Ляпунова [4] решена задача перевода динамической системы из произвольной точки x o G X o С R n в точку программной траектории х ° на обрабатываемой поверхности. Уравнения динамики получены для многозвенного МР с распределенными массами звеньев, кинематическая схема которого приведена на рис. 1. Обобщенные координаты манипулятора п х , П ц , А, М = 1, 2, 3 определяются углами поворота его звеньев. Обобщенными координатами электроприводов являются заряды q ax , q bx , А = 1, 2, 3, протекающие через поперечные сечения обмоток якоря и возбуждения соответствующих электродвигателей. Модель динамики МР получена в форме уравнений Лагранжа-Максвелла [5] с индексным способом записи [6], снимающим громоздкость преобразований аналитических выражений при построении модели динамики МР.

Точка программной траектории системы определена обобщенными координатами п Х и скоростями п Х , 1 °х . Классический способ вывода уравнений динамики дает систему уравнений движения электромеханической системы

( LaXp. ^— L/ M yX M vp^ I ap. + L{, ^Y (ⁿ Y ^{— 2M} Y^ I a^ ) ~g^— ^П в = N X ;

.                                                                                                              (1)

С Хц П ц + C x^v T) p. T) v + L ^ M Y^ I a^ g^ ^ 1 ав = M X '

Здесь c x^ - тензор инерции манипулятора [6], I ax = l ax , I bx = I bx , n x — обобщенные скорости системы, L _aλµ , L _bλµ – тензоры индуктивности, M _λµ – тензор взаимной индуктивности обмо-

ток якоря и возбуждения электродвигателей приводов, I bλ – циклическая скорость, C λ_,µ_ν –

символ Кристоффеля первого рода метрического тензора c x^ , тензор L^: L^L b^_v = ^,

§ V — символ Кронекера, обобщенные силы даются равенствами N x = -R x^ I a^ + U x ,

M x =

-B x^ i i ^ ^-

∂W p

∂η λ

νγ ^∂M νβ

( n )+ L b 'ⁿY ~g--- l ae , где R x^ , B x^ - тензоры, определяющие диссипацию

электромагнитной и механической энергий системы, соответственно, W p (n) — потенциальная

dWP (П)                           „ энергия манипулятора,        – потенциальные силы, действующие на степень подвижно-

∂ηλ сти с номером A, Ux — управление, стесненное ограничением Ux Е Rs, Rs - ограниченное

замкнутое множество, задаваемое из ресурсов управления. Введем возмущения Anx, Anyx, AIax, AIax как разность между текущими и программными значениями обобщенных ко- ординат и скоростей. Условие стационарности движения в точке программной траектории дает следующий интеграл возмущенного движения приведенной системы [1]:

Jx = (Lax^ - LbMy.M^ - (Lax^ - LbMW^ + Lb-^Ane.

Энергия возмущенного движения системы имеет вид

J = ICxLhxn. + 2 (Lax^ - LbM^M^) △ Lx △ L^ + WpA).(3)

Построим функцию Ляпунова V как связку интегралов возмущенного движения системы [4]:

V = J + pJxJx,(4)

где ρ – положительная константа. Так как в стационарном движении (равновесии системы) все обобщенные скорости nx = 0, имеем следующее условие осуществимости стационарного движения

Г ^Y ° °^{о dM ve} °о

^L b ^M γµ ^I aµ _∂η _λ ^I aβ

-

^vY ^d M ^ve °    ^dW p

^L b ^ ^ПТ Ia^{e +} 5П Т ^(П )

Полная производная в силу системы (1) функции V с учетом (5) после проведенных преобразований имеет вид

Выбрав управление в виде

U x = R x^ I a^ - ^aJ x ⁺ ^ д —p^-^)                        ⁽⁶⁾

с положительной константой α, имеем

VV = ^—B Xц ⁿ) X ⁿ) ц ^- P^a^^J x ⁺ ^ A p a ^ ^ JJ x ⁺ ^ A p a ^ •

Исследуем устойчивость движения МР, приведенного на рис. 1. Рабочим органом является инструмент, представленный телом вращения (1 – характеристическая точка рабочего органа). Инерциальную систему координат Oxi свяжем с основанием МР, а подвижную систему координат O’xi (i = 1.2.3) - с третьим звеном, выбрав ее начало в центре инерции тела. По теореме сложения скоростей абсолютная скорость произвольной точки тела v = vo‘ + ш х r ‘ + v',

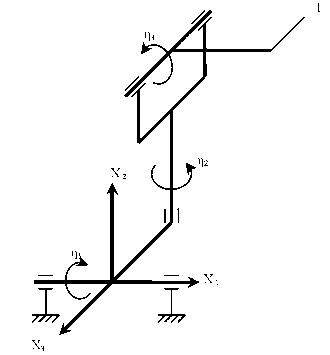
Рис. 1. Кинематическая схема МР

где v o ’ - скорость полюса O ‘ движущейся системы осей, С -ее угловая скорость, v ‘ - скорость точки по отношению к подвижной системе осей, r ‘ - радиус-вектор точки в подвижной системе осей.

Кинетическую энергию рабочего органа определим выражением

^T k = 2 m (iv O 1 2

+ (w + еф) ^ o ‘ (J + еф

где $ _о ‘ -тензор инерции тела, m - масса тела. Предполагая равенство экваториальных моментов инерции тела A и C относительно осей O ’ Х 1 , O ‘ х 2 , учитывая то, что $ _о ‘ = AE + ( В — A)e е, где В - момент инерции тела относительно оси O ’ х 2 , преобразуем (8)

к виду

^т к = 2 m ^|J o ‘ | ² + A( | J | ²

— ше) ) + В (ше + ф) .

Отнесем слагаемые, не зависящие от угловой скорости рабочего органа ф к тензору инерции манипулятора, сформируем тензор s x_p . Кинетическая энергия системы имеет вид

T = 8 _Хц Т] х П ц + 2 Вф ² + Вф ф х П X ■

Здесь ф _х = a i r _iX (i = 1, 2, 3, А = 1, 2, 3), r _iX - тензор, связывающий проекции вектора С на оси подвижной системы координат с эйлеровыми углами п х , a i - направляющие косинусы вектора е в подвижной системе координат. Считая координату ф циклической и определив отнесенный к ф импульс p формулой p = В (ф + ф х П х ), сформируем функцию Рауса и получим следующие уравнения динамики МР с рабочим инструментом

( LaXp

^— L ^{U M} yX М иц )^Iap ⁺ L b^ (ⁿ Y ^{— 2 M} YP, I a^ ) “^^— ^П в = ^— R X^ I a^ ⁺ U X

^ Хц ^V p ⁺ ® X,pv ⁿ p ⁿ v ^{+ L} b (ⁿ Y

_{M T} ⁾ 9M v₃        дф х 9ф _ц

M ^{YP I ap)} On x ^{I ae + p}(an p 8n x ) ^pp =

^{— В} Хц т) p ^—

8W p (n) dn x

Здесь ^ Xp = S Xp — B^ X ^ p , & X,p_V — символ Кристоффеля тензора ^ Xp . Оставим структуру функции Ляпунова (4) прежней. С учетом (4)–(6) имеем:

V = 2 ti XpW n p + 2 (L aA^ — L V^Y M yX M vn> I aX Мац + W p (A^) + pJ _X J x -

Полная производная функции Ляпунова в силу системы (11) имеет вид

^V = -B Xp Tl X ^l p. ⁺ (U X - ^R X^ I ap.')' ⁾ (^pJ X ⁺ ^ д ^А1 ац )

-

P ^d p ^X il p fl X + p|2 ^p il X ni p -∂η µ         ∂η λ

Сумма двух последних слагаемых в выражении V равна нулю, и управление (6) обеспечивает асимптотическую устойчивость движения характеристической точки рабочего органа в точку программной траектории.