Общее уравнение для описания равновесий кислотно-основных систем

В работе [1] предложено общее уравнение для описания кислотно-основного титрования смесей произвольного состава. Обозначенная де Ливье проблема построения модели равновесий кислотно-основных систем в виде единственного уравнения, которое легко исследовать абстрактно-математическими методами, является актуальной задачей как с точки зрения теории кривых титрования, так и с точки зрения практического использования общего уравнения при обосновании и разработке алгоритмов анализа многокомпонентных систем.

При построении общего уравнения кривых титрования в [1] применяют способ рассуждений, при котором результаты физико-химического описания частной системы титрования смеси соляной, уксусной и фосфорной кислот щелочью используют для записи общего уравнения. При таком подходе общность уравнения может быть неполной. В частности видим, что в исследованной образцовой смеси отсутствуют амфолиты.

Проблеме общности количественного описания кривых титрования посвящена недавняя обзорная статья Асуэро и Михайловского [2]. В отличие от [1] авторы обзора строят вывод общего уравнения на основе абстрактной протолитической системы, включающей амфолиты. При этом в качестве компонентов протолитической системы они вынуждены рассматривать такие частицы, как катионы щелочных металлов и анионы сильных кислот, поскольку вывод уравнения строят исходя из условия электронейтральности системы. Такие соли, как хлорид аммония при выводе уравнения не рассматриваются. Авторы работ [1] и [2] ограничиваются рассмотрением только логарифмических кривых титрования. Методы титриметрии с линеаризацией кривых титрования [3, 4] оказываются вне поля зрения теории.

Можно думать, что уравнения, полученные в [1] и [2], являются частным случаем более общего уравнения, из которого в качестве следствий выводятся не только уравнения сигмовидных кривых титрования, но также другие закономерности вне зависимости от способа смешения компонентов, например свойства буферных растворов. Целью работы является обоснование данного положения.

Вывод общего уравнения

В общем случае, как это следует из протолитической теории Бренстеда – Лоури, протолитическая система содержит три типа протолитов: кислоты, основания и амфолиты. Все протолиты взаимодействуют между собой, обмениваясь протоном, и поэтому образуют единую систему. Системный подход позволяет сделать вывод о том, что для закрытой системы должна существовать единственная функция F(pH, с ) = 0, связывающая рН и вектор исходных концентраций протолитов с .

Кислоты и амфолиты будем рассматривать в качестве протонных комплексов H _i B оснований Бренстеда [5], которые с формальной точки зрения являются центрами координации протонов. Координационное число основания В равно его максимальному эквивалентному числу z B . Здесь ограничимся рассмотрением протолитических систем, состоящих только из протолитов с одной центральной группой. В разбавленных водных растворах большинство известных протолитов можно считать неассоциированными. Ион гидроксила является центром координации протона. Анионы сильных кислот имеют z B = 0 и поэтому протоны сильных кислот полностью переходят в ион гидроксония.

Пусть, в общем случае, в гомогенном водном растворе протекает r независимых реакций:

Н + oh <—> Н 2O, i Н + В j <    > Н i В j, где i = 1, zj , а j = 1, m . Из записи (1) понятно, что индекс j обозначает порядковый номер основания. Знаки зарядов частиц в уравнениях реакций опущены для того, чтобы придать им большую общность. Отсюда реакции (1) также распространяются на случай незаряженных оснований, таких как амины. Координационное число j-го основания – это одновременно его максимальное эквивалентное число, которое обозначено символом zj. Кислоты и амфолиты, т. е. предельные и промежуточные протонные комплексы будем для краткости называть просто кислотами.

Построение общего уравнения для количественного описания системы реакций (1) начнем с записи уравнения протонного баланса:

m^z j                         m^z j

c (H) + ££ ic (H i B j ) = [H] + ££ i [H i B j ] + A c (H₂O) .                                 (2)

j = 1 i = 1                            j = 1 i = 1

В левой части уравнения просуммированы исходные концентрации кислот, а справа записаны их концентрации после установления равновесия. Уравнение содержит слагаемое Ac(H2O) = [H2O] - с(H2O). Дополнительное количество воды в системе может возникнуть только за счет расходование щелочи, поэтому

A c (H₂O) =-A с (OH) = с (OH) - [OH] .                                                  (3)

Это уравнение является уравнением гидроксильного баланса системы. Подставляя уравнение гидроксильного баланса в уравнение протонного баланса, получаем уравнение, которое в литературе называют протонным условием [5]: _m z_{j                                   m} z_j

c (H) - c (OH) + ££ ic (H i B j ) = [H] - [OH] + ££ i [H i B j ].                             (4)

j = 1 i = 1                                       j = 1 i = 1

Перейдем к дальнейшему исключению неизвестных из уравнения (4). Для этого воспользуемся определением Н. Бьеррума [6] для среднего лигандного числа n _j . Исходя из определения функции Бьеррума, запишем z_jz_j                                        z_j

£i[HiBj] = nj£c(HiBj) = njc(Bj) + nj£c(HiBj).(5)

i=1                     i=0

После подстановок (5) в (4) получаем mzj

[H] - [OH] = c(H) + ££(i - nj)c(HiBj) - c(OH) - £njc(Bj).(6)

j=1 i=1

Разность [H] - [OH] обозначим так же, как в [1], символом A . Переменные A и n j в уравнении (6) являются хорошо известными функциями от рН раствора:

A = [H] - Kw = 10-pH - 10pH-pKw ,(7)

[H]

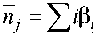
Аналитическая химия

Константы образования р , т. е. константы равновесий (1), обычно вычисляют с использованием таблиц частных ступенчатых констант кислотности или основности по формулам, которые приведены ниже:

ii

1g ^р i = Е Р K a ,( z - 1 + 1) или lg ^Р i = Е ( ¹ Р K w ^- Р K b(z - 1 + 1 ) ) , 1 = 1 1 = 1

где i = 1 ,z и 1 = 1 ,z , а K w - ионное произведение воды. Для простоты будем полагать, что константы равновесий в уравнениях (7) и (8) являются концентрационными константами. Общность уравнения (6) также не нарушается, если считать константы равновесий в (7) и (8) условными константами.

Уравнения (6)–(8) являются записью общего уравнения кислотно-основных равновесий в водном растворе в параметрической форме. Таким образом, задача по восстановлению функции F(pH, с ) = 0 нами решена, причем с небольшим числом математических процедур.

Рассмотрим другие варианты представления уравнения (6). Вначале обратим внимание на то, что с точки зрения теории эквивалентов коэффициенты i = z_i j имеет смысл эквивалентных чисел соответствующих кислот H i B j . Отметим также что, эквивалентные числа сильной кислоты и щелочи равны единице. Формально, для сильных кислот n = 0 , а для гидроксила ^ = 1 независимо от рН раствора. Общее число кислот в системе обозначим как n, а общее число оснований – l . Раскроем двойную сумму и перенумеруем слагаемые в уравнении (6). Кислоты принимают номера a = 1, n . А основаниям назначим номера b = 1, 1 . Теперь уравнение (6) приняло более простой вид:

А = Е F a C a - Е F b C b , (9) где F_a = z_j;j - n j и F_b = n j . Переменные F_a и F_b в [1] названы функциями протонной диссоциации и функциями протонной ассоциации, соответственно.

Заметим, что выражение А = [H⁺] - [OH^-] входит во все уравнения, описывающие частные протолитические системы (поскольку оно присутствует в общем уравнении). Однако в литературе А не имеет специального названия, что создает определенные терминологические неудобства. Будем называть А показателем (характеристикой) протон-гидроксильного баланса. Этот термин соответствует физико-химической сущности А . Так в нейтральном растворе показатель протон-гидроксильного баланса равен нулю. Причиной нейтральности среды является взаимная компенсация воздействий кислот и оснований на среду, поскольку при этом Е F_ac_a = Е F_bc_b .

По своей математической природе функция (9) является билинейной формой. Эти свойства общего уравнения используют в методах потенциометрического анализа с линеаризацией кривых титрования [7].

Уравнение (9) перепишем в другой, более удобной для исследования и вычислений форме. Каждое слагаемое в уравнении умножим и разделим на соответствующее эквивалентное число z_i j . Это равносильно тому, что концентрацию протолитов мы выражаем в молях их эквивалентов. При этом переменные F a и F b заменяются нормированными величинами k a и k b , которые могут принимать значения только в интервале от 0 до 1. Результат преобразования запишем как

А = Е k a N a - Е k b N b , (10) где k_a = 1 - n j I z j и k_b = n j / z j . Эти переменные имеют простое физико-химическое содержание. Переменная k_a характеризует степень депротонирования кислоты, а k_b – степень протонирования основания.

Форма уравнения (10) легко запоминается, что позволяет просто описать его на вербальном уровне. Поэтому при решении частных задач нет необходимости начинать построение модели с записи балансовых уравнений и уравнений закона действующих масс (ЗДМ). Можно воспользоваться правилом записи общего уравнения: «Показатель протон-гидроксильного баланса раствора равен сумме парных произведений нормальных концентраций кислот (и амфолитов) на степени их депротонирования за вычетом суммы парных произведений нормальных концентраций оснований на степени их протонирования » . Степень депротонирования сильной кислоты не зависит от рН и всегда k (HВ) = 1, поскольку реакция НВ + Н 2 О → В^– +Н 3 О⁺ идет до

Голованов В.И., Кузнецов С.М.

конца. Степень протонирования щелочи k (NaOH) = 1, так как реакция Na 2 O + H 2 O → 2Na⁺ + 2OH^– практически необратима.

На практике применяют также дифференциальную форму уравнений (6), (9) или (10). Это, например, зависимость буферной емкости раствора от рН или уравнение дифференциальной кривой титрования. Применяя к уравнению (10) выражение его полного дифференциала, имеем

— = d^k N _ dk^N + d N ^ k _ d N L k . dpH dpH ^a dpH ^b dpH ^a dpH ^b

Из уравнения (11) получаем формулу для вычисления буферной емкости:

_ d N (H) _ d N (OH) _ _v d k _v d k_b d A

* = _ dpH = dpH = E dpH Na _ E dpHNb _ dpH, d kQ      d kb       E i (i_ n )P, [H] ‘ где —- =--- = 2,3 ——=—, , — z , dpH   dpH 1 + E Д[н]'

dA = 23 [h]2 + K dpH ,     [H]    .

Заметим, что в выражение (13) входит коэффициент крутизны функции образования, формула которого хорошо известна [6].

Нелинейную по рН форму уравнения (12) используют для вычислений буферной емкости, а линейную анаморфозу уравнения применяют при потенциометрическом титровании многокомпонентных смесей кислот [8].

Обсуждение результатов

Полученное нами общее уравнение (10) можно использовать как для описания многокомпонентных буферных растворов, так и для описания кривых титрования. Покажем, что предложенное Р. де Ливье [1] уравнение кислотно-основного титрования является следствием уравнений (9) и (10).

Опираясь на результат моделирования титрования смеси соляной, уксусной и фосфорной кислот щелочью де Ливье постулирует существование общего уравнения кривых титрования вида

V b = E F a c a ^_A

Va E FbCb° +A , где Vb – добавляемый объем смеси оснований к начальному объему Vа смеси титруемых кислот. Верхний индекс «ноль» указывает на начальные концентрации веществ в смешиваемых растворах. Уравнение (15) описывает сценарий, при котором произвольную смесь кислот титруют произвольной смесью оснований. Уравнение кривой титрования смеси оснований смесью кислот записывается в обратносимметричной по отношению к уравнению (15) форме:

у   У Fbcb0 + A a_ =       b b

.

V b E F a c a _A

В [1] переменные Fa и Fb вычисляют с использованием выражений для мольных долей соот- ветствующих протолитов:

F a =a (H „. 1 B) + 2 a (H „ -2 В) + 3 a (H „ _ з В) + _ n a (B) ,                                       (16)

F_b =a (H 1 A) + 2 a (H 2 A) + 3 a (H₃A) + .„ n a (H n A) .                                       (17)

Формула для вычисления F_a амфолитов автором [1] не определена. Отсюда теория де Ливье имеет ограничения. В примере [1], взятом для обобщения, нет амфолитов.

Вместе с тем этот недостаток несложно исправить, если воспользоваться нашим уравнением (9). Видим, что уравнение (17) является одной из форм записи функции Бьеррума [9]. Отсюда F b = n j . С другой стороны, при выводе уравнения (9) нами показано, что по своей форме F_a для кислот и амфолитов не различаются. Поэтому уравнение (16) следует переписать как

^Fa = E ^{( z} j ^{_ i ) a} / = ^z j ^_ nj .                                                                  ⁽¹⁸⁾

= 0

Понятно, что вычислять F a и F b через функцию образования гораздо проще. Кроме того, формулы становятся компактными и удобными для анализа.

Аналитическая химия

Легко убедиться, что уравнение (9) переходит в уравнения де Ливье с учетом того, что при тированиии

с

a

сa0Va              сb0Vb сb.

ab    ab

Уравнения вида (15) полезны при вычислениях титровальной доли p или погрешности титрования 5 r = p - 1. Уравнение для вычисления p найдем из уравнения (10). Пусть смесь кислот титруют смесью оснований, добавляя переменный объем V b с суммарной концентрацией £ N b к объему титруемого раствора V_a , общая концентрация которого £ №0 . Решение уравнения (10)

относительно титровальной доли имеет вид

Vb £ Nb _ £ kaqa-А/ £ №0

Va £ №0 £ kbqb + А/ £ Nb где qa и qb – мольные доли соответствующих протолитов в исходных растворах. Если разведением титруемого раствора пренебрегают, то второй член в знаменателе правой части уравнения исчезает. Переставляя местами в уравнении (19) числитель и знаменатель получаем уравнение, описывающее титрование оснований смесью кислот.

Компоненты протолитической системы при титровании можно группировать по признаку их вхождения в исходный титруемый раствор Vs или в раствор титранта Vt вне зависимости от кислотно-основных свойств компонентов. На это обстоятельство указывают в [1]. Например, в качестве примесей кислоты могут присутствовать в основаниях и наоборот. Исходя из того, что загрязнение кислоты ее солью равносильно загрязнению кислоты эквивалентным количеством щелочи, а присутствие солей оснований в растворе оснований равнозначно загрязнению раствора сильной кислотой, уравнение (15) примет вид

V _ £ kaNQs - Ns (OH )-A

Vs £k^ - N0 (H) + A

При обратном титровании дробь в правой части уравнения (20) обращают.

Уравнения кривых титрования в записях (15), (19) и (20) полезны при восстановлении зависимости V t от рН. Такую кривую называют [1] выходной кривой (the progress curve). Чаще рассчитывают зависимость рН от объема титранта. Выходную кривую получают в виде алгебраического решения. Тогда как зависимость рН от V t , т. е. логарифмическую кривую титрования, можно рассчитать только численно. С математической точки зрения уравнение выходной кривой является обратной функцией для уравнения кривой титрования.

Расчеты кривых титрования обычно выполняют с использованием метода Ньютона. Для этого общее уравнение (10) при титровании кислот основаниями записывают в виде:

F( pH , N ⁰ ) = V s £ k a N 0 - v_t £ kN -A = 0,                                     (21)

где v s _ V s / ( V s + V_t ) и v_t _ V_t / ( V s + V_t ) - объемные доли титруемого раствора и раствора титранта в их смеси. Если титруют основания кислотами, то уравнение (21) заменяют на F (pH , N 0 ) = V t £ k a N⁰ - v s £ k b N b -A = 0.

Дифференциальную кривую титрования раствора кислот щелочью вычислим по формуле dpH _ VscOh я-1 d VOH (V + Voh ) 2

Аналогичная формула справедлива в случае, если титрант – это сильная кислота. Из сравнения уравнений (22) и (12) видим, что полученную экспериментально дифференциальную кривую титрования можно линеаризовать, пересчитав ее в линейную по N_a ⁰ переменную:

0 ( dpH

Z _ c OHU V 2

V s + V oh

1 (Vs + VOH ) Tff      di pH = V.-dk^N,0.

V_s          dpH ^a

В качестве численного примера рассмотрим вычисление состава и буферной емкости универсальной буферной смеси в зависимости от рН буферирования. Смесь готовят из пяти ( n = 5) одноосновных кислот и щелочи. Общую концентрацию кислот примем равной 0,1 н. Причем все кислоты присутствуют в эквимолярных количествах. Показатели констант кислотности образуют арифметическую прогрессию: p K i = 3 + 2( i – 1). Общие уравнения (10) и (12) в данной задаче примут вид:

3OH) = n "1 Z - y- ,(

∑ca л =n-1£ c *У kУ d^-■

^{∑ a ∑ a} dpH_a

Расчеты выполним в электронных таблицах.

Результаты количественного описания буферной смеси приведены на рисунке. В данном примере нас, прежде всего, интересовали вычислительные аспекты применения общего уравнения. Отметить, что использование в качестве аргументов уравнений (10) и (11) функций образования дает не только теоретическое, но и вычислительные преимущества.

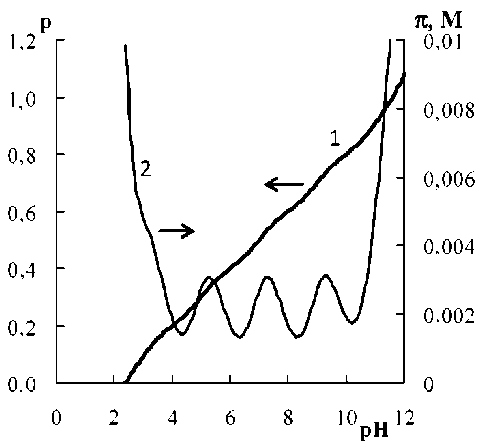
Выходная кривая (1) и кривая буферной емкости (2) универсального буферного раствора (пояснения в тексте)

Расчеты в электронных таблицах по уравнениям (23) и (24) существенно облегчаются с использованием процедур-функций, текст которых приводим ниже:

Public Function FormFunc( lgK As Range,_ pX As Variant) As Variant 'Вычисление функции Бьеррума при 'произвольном числе ступенчатых констант.

Dim i As Integer

Dim N As Integer

A = 0: B = 1

For i = 1 To N

A = A + i * 10 ^ (lgK(i) - i * pX)

B = B + 10 ^ (lgK(i) - i * pX)

Next i

FormFunc = A / B

End Function

Public Function SlopFormFunc (lgK As Range, _ pX As Variant) As Variant

'Вычисление крутизны функции Бьеррума.

A = 0: B = 1

For i = 1 To N

A = A + i * 10 ^ (lgK(i) - i * pX)

B = B + 10 ^ (lgK(i) - i * pX)

Next i

FF = A / B

Num = 0: D = 1

For i = 1 To N

Num = Num + i * (i - FF) * 10 ^ (lgK(i) - i * pX)

D = D + 10 ^ (lgK(i) - i * pX)

Next i

SlopFormFunc = Num / D ^ 2

End Function

Аналитическая химия

Общее уравнение равновесий в кислотно-основных системах можно использовать в следую- щих приложениях:

• 1)    для расчета логарифмических и дифференциальных кривых титрования;

• 2)    для расчета рН и буферной емкости буферных растворов произвольного состава;

• 3)    при выводе уравнений для приближенных расчетов равновесий;

• 4)    для генерирования и исследования алгоритмов потенциометрических методов анализа с линеаризацией кривых титрования.

Пункты 3 и 4 проиллюстрируем примерами.

Известную формулу для расчета рН буферного раствора, составленного из кислоты НВ и ее соли, получим из уравнения (10), переписав его с учетом граничных условий задачи в виде

A =

1 + K a 1 [H]

c (HB)

K a ^{– 1}[H]

1 + K a 1 [H]

c (B)

Полагая A » 0, имеем уравнение Гендерсона pH = pKa + lg

c (B) c (HB) .

Из уравнения (10), накладывая на него очевидные из условия задачи ограничения, найдем уравнение графика Грана для определения содержания суммы оснований при титровании сильной кислотой. Будем полагать, что на кривой титрования существует область рН, в которой степени протонирования k_b всех оснований равны единицы. Отсюда следует, что в кислой области

( V s + V )l 0 pH = V ⁰(H) - V s £ N 0 = Vc ⁰(H) - V teq C ⁰(H). (27)

Точка пересечения прямой (27) с осью объема титранта соответствует его эквивалентному объему V_t,eq . Отсюда находят суммарную концентрацию оснований ∑ N_b ⁰ .

В заключение отметим, что впервые общее уравнение кривых кислотно-основного титрования было опубликовано в руководстве [9]. При выводе уравнения учитывали, также как автор [1], баланс по протону и условие электронейтральности. Однако уравнение [11], так же как уравнение [1], не описывает случай титрования амфолитов. Разведением титруемого раствора титрантом в [9] пренебрегают.

В работе [10] показано, что общие уравнения кривых не только кислотно-основного, но также комплексометрического, осадительного и окислительно-восстановительного титрований можно получить на основе закона постоянных отношений (ЗПО) [11]. При выводе на основе ЗПО исключаются трудности, связанные с записью условия электронейтральности для системы протолитов произвольного состава. В данной работе эти трудности преодолеваются за счет комбинирования уравнения протонного баланса с уравнением гидроксильного баланса. Использование этого сочетания делает вывод общего уравнения более наглядным и, кроме того, подчеркивает роль воды как протолита в балансовых соотношениях.