Обтекание пластины на режиме сильного взаимодействия при наличии массообмена

Исследование влияния массообмена через поверхность тела на поток представляет значительный интерес, так как при этом можно существенно уменьшить тепловые потоки и трение у поверхности, а. также повлиять на. распределение давления около тела. Исследование вдува газа по нормали к поверхности тела в сверхзвуковой поток показало, что для течений этого типа, важную роль играет распространение возмущений вверх по потоку, и при решении необходимо учитывать краевое условие на. заднем конце тела. [1]. Заметим, что в отсутствие вдува происходит локализация распространения возмущений и реализуются сверхзвуковые течения со «свободным взаимодействием» [2,3].

При гиперзвуковом внешнем обтекании характер течения в пограничном слое значительно изменяется, так как плотность газа, в нем уменьшается, а. толщина, вытеснения существенно возрастает. Для случая режима сильного взаимодействия было получено автомодельное («трехчетвертное») решение в [4,5]. В работе [6] с использованием приближенной формулы «касательного клина» впервые было показано, что на. режиме сильного взаимодействия задача, в окрестности передней кромки имеет однопараметрическое семейство решений, зависящих от некоторого собственного числа. В этом случае возмущения могут распространяться вверх по потоку на. вето длину тела. В работе [7] вместо приближенной формулы «касательного клина» невязкая возмущенная область течения рассмотрена, на. основе гиперзвуковой теории малых возмущений. Были получены система, дифференциальных уравнений, описывающая гиперзвуковое течение между скачком уплотнения и пограничным слоем, а. также уравнения пограничного слоя и исследовано влияние температурного фактора, на. значение собственного числа. Исследование вдувания газа, в гиперзвуковой поток на режиме сильного взаимодействия проведено в работе [8]. Как и в [6], для определения индуцированного давления использована, формула, «касательного клина» и показано, что в окрестности передней кромки решение не является единственным. В [8] сформулированы краевые задачи для определения автомодельного решения и для нахождения собственного числа. Однако собственное число, равное а ~ 0.23, определено только для предельного случая N ^ то. Физический смысл параметра подобия N - квадрат отношения характерной толщины области невязкого течения, связанного с вдувом, к толщине пограничного слоя.

В данной работе исследуется распределенный вдув через поверхность пластины, обтекаемой на. режиме сильного взаимодействия. Для описания течения в ударном слое вместо приближенной формулы «касательного клина» используется система уравнений, полученная с помощью гиперзвуковой теории малых возмущений. Проведены исследования функций течения и собственных чисел в зависимости от показателя адиабаты у, температуры поверхности пластины Т* и скорости вдува газа П*.

2.    Постановка задачи

Рассматривается гиперзвуковое обтекание вязким газом полубесконечной тонкой пластины под нулевым углом атаки при числе Маха невозмущенного потока М_Д = ЦД /аД ^ 1. В набегающем потоке иД - скорость. рД - давление, рД - плотность, аД - скорость звука. Температура поверхности Т* считается заданной и постоянной. Рассматривается совершенный газ с отношением удельных теплоемкостей у = с*/с* и коэффициентом вязкости цД, линейно зависящем от температуры. Вводится декартова система координат, начало которой расположено на передней кромке пластины. Компоненты вектора скорости п*, н* направлены вдоль осей координат х*, у*. Область течения за присоединенным головным скачком разделяется на область невязкого течения и вязкий пограничный слой (рис. 1).

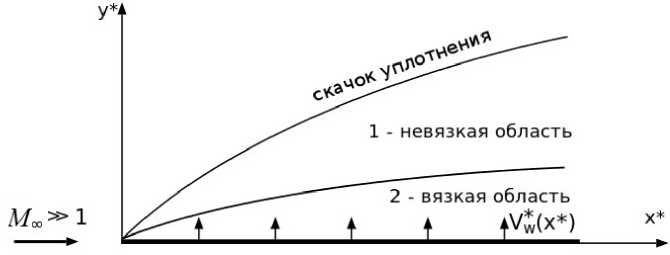
Рис. 1. Гиперзвуковое обтекание плоской пластины при наличии массообмеиа на. поверхности

Уравнение скачка: у* = Y*(x*) причем его наклон: dY*/dx* = О(М ^—1). Внешняя граница пограничного слоя: у* = 8*(x*Y Детальная структура области течения за скачком может быть найдена в результате совместного решения двух систем уравнений в частных производных: одной гиперболической, а другой параболической при выполнении условий сращивания на внешней границе пограничного слоя: непрерывности давления и равенства наклона линий тока. Режим взаимодействия определяется величиной параметра: X = М 3/Не^Д [9], где Re Х*Д = рД ^иД ^х* /р-Д - число Рейнольдса, вычисленное по текущему значению продольной координаты х*. При х = 0(1) - реализуется умеренное взаимодействие, а при х ^ то - сильное взаимодействие. Однако, как показано в [9] для двумерных течений, режим сильного взаимодействия фактически реализуется при х > 3. В случае обтекания полубесконечной пластины при большом, но конечном значении М_Д в окрестности передней кромки будет возникать область сильного взаимодействия, ниже по течению - режим умеренного взаимодействия, а еще ниже там, где х ^ 0(1) - режим слабого взаимодействия. Заметим, что в предельном случае, когда число Маха М_Д ^ то на всей пластине реализуется режим сильного вязко-невязкого взаимодействия.

Предполагается, что через проницаемую поверхность пластины по нормали к ней производится непрерывный распределенный вдув/отсос газа с заданной скоростью Т*(х*, 0). Рассматривается случай, когда скорости вдува/отсоса порядка скорости нормальной компоненты, возникающей в ламинарном пограничном слое, и, следовательно, отсоединения пограничного слоя не происходит [8].

3.    Уравнения движения в невязкой области

Рассматривается течение в невязкой области 1 (рис. 1) между скачком и внешней границей пограничного слоя в предположении, что М_— ^ 1 и реализуется режим вязконевязкого взаимодействия. Считается, что невязкая область 1 описывается стационарными двумерными уравнениями Эйлера (неразрывности, импульса и энергии):

д (р*и*) дж*

д (р^*)

+ др*

*              * ди*

ри*---+ р v*^— = дж*        др*

* * дv*     „ „,dv*

р*и*---+ p*v*-— = дж*        др*

Р*и*    + P*v*    = 3Р* ( дж*       др*       \

ди*

= 0, др* дж*’ др* _-

др*' и*^ + " дж*

.. др* у др*

Для оценки максимального продольного размера области умеренного и сильного взаимодействия ж1 будем считать, что на ее границе вниз по течению гиперзвуковой пара- 1

метр взаимодействия х = М— /Re,2*_— = 1. Следовательно, характерный размер области ж1 = М 6 v^/U *, г де v * = ц— /рД ^_ кинематический коэффициент вязкости. На основании соотношений Рэнкина-Гюгонио при больших числах Маха получаем, что поперечный размер невязкой области 1 имеет порядок р* ~ ж*/М_—, а нормальная компонента скорости - v* ~ U*J М_— Далее вводятся безразмерные переменные [7]:

^М 6р        ^М 5р*            *   *

• ^ж = ^—* ^ж, р = ^—* р, ^и = ^и*^и, ^v = ., ^v Р = Р—Р, р = р — р- (2) ^U сю           ^U сю                    ^М —

Поверхность скачка уплотнения в безразмерном виде задаётся в форме р = Ү8(ж). В безразмерных переменных (2) система уравнений Эйлера (1) приводится к виду

д(ри) дж ди

+

д (pv)

ди

др

^р“вх ^{+ р}"ар =

-

дv

дv

^ридж ^{+ ри}а"₈

др др ридж + рР9у = 3Р

= 0, м—у дР, 1 др

-

у др, ^др    ^др

(^иэж ⁺ ''фЕ

Для определения течения в невязкой области удобно ввести функцию тока М? удовлетворяющую уравнению неразрывности:

дМ дМ

др =^ри,дж = -^р"

Учитывая (4) и переходя к переменным Мизеса: (ж,р) ^ (ж, М) г де ж = ж, можно систему (3) привести к виду ди     1 др 1      др 1

^идж    р дж М 2 у ^V сіМ М 2 у’

Cv     Ср 1

~— — —_—■—.

дж    дМ 3

dv _ 1 др —  —---: .

дМ    3Рр дж

При преобразовании уравнения энергии в (3) использовано уравнение неразрывности и учтено, что в гиперзвуковом приближении в невязкой области 1 за скачком и = 1 + О(М—2). После введения функции энтропии Е = р/р7 система уравнений (5), описывающая течение в невязкой области, приводится к виду dv    Эр

У дх    дф1

dv     Е 5 др дф     ^р1+у дх"

В соответствии с [4,5] скачок уплотнения рассматривается как известное автомоделвное «трёхчетвертное» решение плюс возмущение п-го порядка:

Y_s = Ах 4 (1 + сщх^и),                                   (7)

где А, а_п - некоторые константы, которые зависят от граничных условий, п - собственное значение, которое определяет порядок возмущения поверхности скачка уплотнения. Соотношения Рэнкина-Гюгонио, преобразованные в соответствии с (7), учитывая преобразования Мизеса, дают следующую систему для нахождения параметров потока за скачком:

и = 1,

_  2 dYs у +1 dx 1

2у zdY.x^{2 р} = у+г( d^) , у + 1

Р = ----7‘

У - 1

Выражение для энтропии Е с учетом (7), (8) и того факта, что на скачке уплотнения ф = Y_s, можно записать в виде

е ■ ■<(   ■у( а ⁾³ Л+82^(п+ дф⁾*).

8(у + 1) у + 1 ф         3         А

Совершим ещё одну замену переменных (х, ф) ^ (^,у) ^гД^е £ = X, у = ф/Ү₈. В этих переменных на скачке значение координаты у = 1. По аналогии с возмущением поверхности скачка уплотнения, значения скорости и давления в невязкой области ищутся как совокупность главного члена и возмущения п-го порядка.

^v = у+у уҮ (Шу ) ⁺ aWTMy

Р =     (Y^) (Лз(У) + аДпРп у + 1 \ d^

(Ю)

Переходя в системе (6) к новым переменным (£, у), учитывая (7), (9), (10) и собирая в уравнениях члены одного порядка, получаем систему из четырех нелинейных дифференциальных уравнений, описывающих течение в невязкой области (рис. 1):

- Vo (у) = 0,

4      1     ³    16

^Р(у) ^- у^⁽у) ⁺ о (^{п -} 7 П« ( у ) ⁺ ,. "⁽" ^{+ 1)V}0⁽у) = 3 х 4 2           9

Р0 (у) - у^ОЪ)

-

0,

V ‘(ту) =

-

у 37

^{V (}у)

-

-

1+ ¹

р 7

1 у

(у)

( 3 ^Ро ⁽у^{) +} у^Р‘ ⁽у)),

+2 7 3

-

Р

1+ ¹

у 37

1+ ¹

Р 7 ро

(у)

-

^Рк (у) ⁺

7 + 1V‘(у)

Рп(у)

(У)

ро СУ)

+

(И)

/     1              8             4п

(^И — 2/ ^Рп(У = 37^{(П + 1} V 3

16 7

-

-

1) V‘(у)

-

("+4)("+4)

у 37

.

Р э⁷ ( у )

Граничные условия для системы (11) получаются из соотношений (8) на скачке уплотнения при у = 1:

Ро (1) = Vo (1) = 1,РД1) = V (1) = 0.                       (12)

4.    Уравнения движения в области пограничного слоя

Для пограничного слоя в области 2 (рис. 1) используется система уравнений из [10] в безразмерных переменных (2):

ди ди

"дх

+ " яду

дТ дТ u 7 -"дХ + "ау - РЩ

Ir ( у" ⁺ Тт ( рЛ =⁰, дх ду

1 dp 1 д

7М, р dx ⁺ М, р ду 1 ^dp = 7 - ^{1 ( д}" ⁾² + dx  М, р   ду

(ртд")

1 д

М, РдУ

,

( ст^ ), \ ду /

где T - безразмерная температура, С - константа в законе вязкости Чепмана: д*/д, = СТ*/Т* = СТ. В системе (13) число Прандтля полагается единицей: Рт = р*с*/А* = 1, где д* - динамический коэффициент вязкости, с* - удельная теплоёмкость при постоянном давлении, А* - коэффициент теплопроводности. Для дальнейшего преобразования системы (13) вводится функция 5 как аналог энтальпии:

Т = ^М^(5 - u2).                       (14)

Производится переход к новой функции тока: Ф = Мус. а также к перемену ной Дородницына: г = М2 J рdу. После применения преобразования Дородницына: о

(х,у) ^ (Х,г), г де X = х, к уравнениям импульса и энергии из (13) с учетом (14) получается следующая система:

дФ д²Ф дг дХдг

дФ д2Ф = - ^r-l дР (5 - " ² )+ ср| З Ф , дх дг²      27р дх             дг³

дФ д5 - дФ д5 =_С д25

дг дХ дХ дг    Р дг2 .

Сращивание решений для вязкой и невязкой областей производится на внешней границе пограничного слоя из условия непрерывности давления и нормальной компоненты скоро-7 - 1

сти. С учетом введенной энтальпии (14), толщина пограничного слоя 5 =---- J (5-u²)dг. ²Р 0

Так как на внешней границе пограничного слоя и_е = d6/dX, то выражение для нормальной компоненты скорости и_е на границе областей

∞

Ue

Ч2 £ (I /(s -    '•

Давление на границе пограничного слоя определяется из решения (10) для невязкой области при ту ^ 0. Так как dY_s/d^ определяется из (7), то следовательно, можно искать давление в виде

I = Вх- ² (1 + Q_nxⁿ),                                (17)

где В и Q_n - некоторые константы, которые связаны с константами А и a_n. С учетом этого решение системы (15) по аналогии с решением в невязкой области ищется в следующем виде, зависящем от новой переменной е:

Ф = 2(ВС)2х4 (/о«) + Q^/M?)), s = So(^) + Q^s^,                       (18)

^e 2( вс ) 2 х 4 ‘

Совершая переход в (15) к новым переменным (х,г) ^ (хД), г де х = х, с учетом (18), получается система из четырех уравнений на нулевые и п-е приближения энтальпии и функции тока, которые описывают течение в вязкой пристеночной области:

/О’’(е) + маш +^1-1 (So(€) - /02(e)) = 0, /"’(e) + МОК (e) - (4п +²^⁾)/0 (ОД (e)+

+(4п + ОДОМ) + ^1-1 s_n(e ) = ²     (п - 2) х           (19)

x(so(^) -/02(e)) -лж sMMMeao (e) = o, s" (e)+мем (e) - 4n/o (osn(o + (4п+1)/„(e)so «) = ш«).

Для решения системы обыкновенных дифференциальных уравнений необходимо задать краевые условия на поверхности пластины и на внешней границе пограничного слоя. Учитывая порядок системы (19), необходимо иметь всего десять условий. При выходе на внешнюю границу пограничного слоя п ^ 1. Это условие на основании (14) и того, что М^ ^ 1 равносильно s ^ 1. Считается, что возмущения энтальпии и скорости затухают при выходе на внешнюю границу. На пластинке поддерживается постоянная температура, соответствующая некоторому известному температурному фактору s_w.

Согласно постановке задачи на пластинке осуществляется нормальный вдув или отсос газа. Для продольной компоненты скорости остается в силе условие прилипания. Следовательно, граничные условия в безразмерных переменных (2) запишутся в виде

п(х, 0) = 0, и(х, 0) = К(х).

С другой стороны, уравнения (4) после изложенной выше двойной замены переменных (х,у) ^ (х, г) ^ (х,е) приводятся к системе г     п = /о (e)+Q"X"/" (e), м^ри + ІІп = -(ВС) х—4 (/o(e) + (4п + 1)Q"x"/"(e) - e(/0(e)+ ^хП/"(e))).

После подстановки заданных граничных условий система приобретает вид

/0 (0) = & (0) = 0, 4   1 гВ\2                  1

/о(0) + (4п + 1)Q„xⁿ/_n(0) = -7—- — (c) (1 + Qnxⁿ)Vw (x)x4.

Из второго уравнения данной системы следует вывод, что для автомодельности задачи необходимо вдувать газ со скоростью VW_; = kx^{- 4}, где к - константа. Точно такой же результат был получен в более ранних работах [11] по исследованию автомодельных гиперзвуковых течений при наличии массообмена.

Следовательно, граничные условия имеют вид

/о(0) = - A-Т ⁽ В ) ² к, 7^{—1 S} w VC/

/п(0) =--4^ (В) 2 Г^Т,

7 — 1 S_W\C J 4п + 1 S»(0) = 0, S o (0) = Sw, /О(0) = /' (0) = 0, /О’ (то) = S o (to) = 1, /^(то) = S „ (to) = 0.

Согласно выражениям (20) массообмен на поверхности пластины при заданной ее температуре определяется величиной параметра к. Положительные значения к соответствуют вдуву в поток, а отрицательные - отсосу в пластину.

5.    Сращивание давления и нормальной компоненты скоростина границе двух областей течения

Краевые задачи (11), (12), (19) и (20) для обеих областей течения (рис. 1) не являются замкнутой системой. Для их решения необходимо найти дополнительное условие на собственное значение п. Используется сращивание на границе между областями нормальной компоненты скорости и давления. Из невязкого течения (10) при 7 ^ 0

"(0) = -2-fVo(0) + anx"Vn(0)), 7 + 1 ax

Р(0) = T+i (^) (Ро(0) + а„хПР„(0)).

Те же параметры со стороны вязкой области получаются из (16) и (17), учитывая распределение давления в пограничном слое:

". = 2—1Г (1 /(S — "А

• 2 ax х р о             '

6.    Результаты численных расчетов

р = Вх^-2 (1 + Q_nxⁿ).

В результате сращивания получаем интегральное условие для определения собственного числа п:

Цп) = Ро(0) (К(0) + |(4п + 3)V0(0)) + ^3°- ( р _п (0) + 3(4п + 3)РО(0)) х х(4п + 3)(1 + ^Л(П)) =0, ^

a = / ( S o ( ^ ) — / 0А))а

Л(п) = О (2/0«)£ (О — SA))<

Интегральное соотношение (21) замыкает краевую задачу, состоящую из систем дифференциальных уравнений (11), (19) и соответствующих краевых условий (12), (20) для описания обтекания гиперзвуковым потоком вязкого газа полубесконечной пластины под нулевым углом атаки при наличии массообмена на ее поверхности.

Для совместного численного решения уравнений (11), (12), (19), (20) и (21) применялся метод Рунге-Кутты 4-го порядка точности для невязкой области и прогонки для пограничного слоя. В результате определена зависимость собственного числа n(S_w , у,к) от определяющих параметров задачи. На рис. 2 приведены зависимости собственного числа п от интенсивности вдува к для значений температурного фактора S_w = 0.75,1,1.25,1.5 при у = 1.4. На рис. 3 представлены результаты расчетов для теплоизолированной пластины S_w = 1 при значениях показателя адиабаты у = 1.2,1.4,1.66. На рис. 2 и рис. 3 для сравнения приведены результаты, полученные в рабоах [6,7] при исследовании обтекания пластины при отсутствии массообмена.

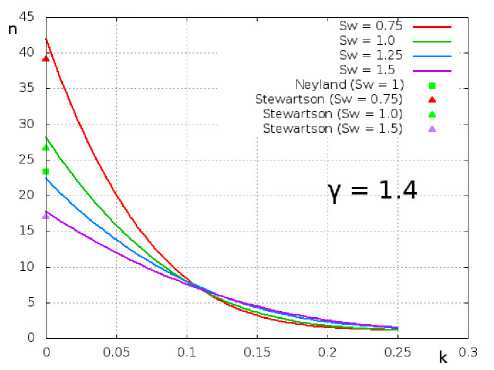
Рис. 2. Зависимости n ( S _w , к) на режиме вдува при у =1.4

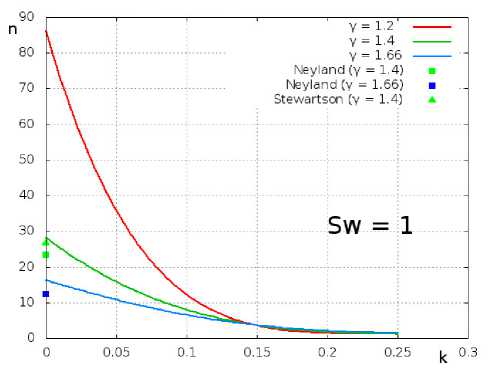
Рис. 3. Зависимости п(у, к) на режиме вдува при S _w = 1

Отличие полученных в данной работе результатов от [7] составляет около 3%, а от [6] -около 6%. Заметим, что в [7] для описания невязкого течения использовалась гиперзвуковая теория малых возмущений, а в [6] - приближенная формула «касательного клина». Учитывая существенно нелинейное поведение собственных чисел и зависимость от множества параметров, соответствие можно считать достаточно хорошим. Из полученных результатов можно сделать несколько выводов. Во-первых, собственное число п существенно возрастает при уменьшении показателя адиабаты у, температурного фактора на пластинке Sw и коэффициента массообмена к. Увеличение собственных чисел в этом случае означает ослабление влияния возмущений, так как Ys, Рф Рп, Sn, fn ~ хп, где ж € (0,1]. Фактически это означает, например, локализацию возмущенного течения в окрестности задней кромки при рассмотрении пластины конечной длины. Во-вторых, при увеличении скорости вдува (к > 0.25) собственные числа достаточно быстро уменьшаются и престают зависеть как от температурного фактора, так и от показателя адиабаты и устремляются к 1. Это означает, что влияние краевых условий на течение в области, лежащей выше по потоку, должно быть достаточно сильным. Физическое объяснение этого явления связано со значительным увеличением толщины дозвуковой части пограничного слоя. Отметим, что в [6] для предельно сильного вдува на холодной пластине было получено собственное число, равное примерно 0.23.

На рис. 4 и рис. 5 приведены профили энтальпии 8o(i) и возмущения энтальпии 8_П(Д в пограничном слое от параметра массообмена к = -0.2, -0.1, 0, 0.05, 0.1 для случая у = 1.4, S_w = 0.75. Отсос газа приводит к существенно му наполнению профиля энтальпии 8о(Д и росту теплового потока, а вдув - к его уменьшению (рис. 4).

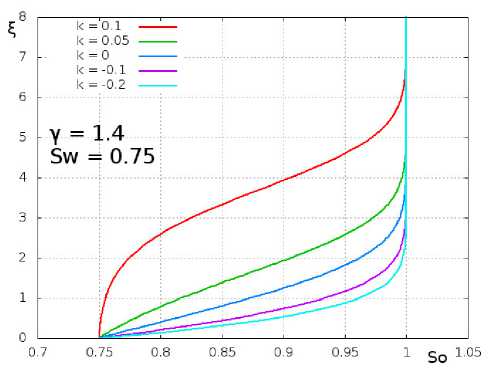
Рис. 4. Профиль энтальпии 80(5, к) в пограиичиом слое при у = 1.4 и 8 ^ = 0.75

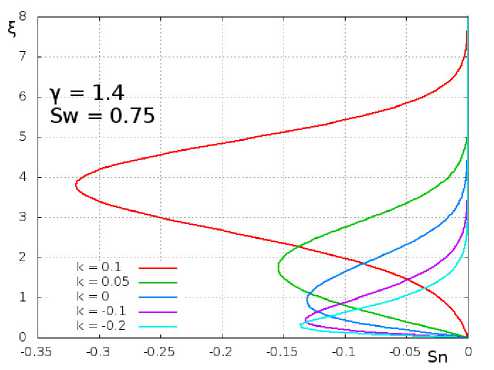
Рис. 5. Профиль возмущения энтальпии 8 ^( 5, к ) в пограиичиом слое при у = 1.4 и 8_W = 0.75

Следует отметить интересное поведение профилей возмущения энтальпии 8П(Д в зависимости от массообмена (рис. 5). При отсосе газа возмущения энтальпии существенно смещаются к поверхности пластины и располагаются в пристеночной части пограничного слоя, при этом толщина пограничного слоя уменьшается. При вдуве газа толщина пограничного слоя, естественно, увеличивается, максимум возмущения профиля энтальпии смещается от поверхности пластины, но теперь он располагается в средней части пограничного слоя. Если вспомнить полное выражение для энтальпии (18), то можно прийти к выводу, что при отсосе газа возмущения энтальпии наиболее интенсивно распространяются по пристеночной части пограничного слоя, а в случае вдува - по центральной части.

Для построения продольной компоненты скорости в пограничном слое следует учесть, что она задается соотношениями:

п = /о (е) + Qпж^п/п ю,

"

^Qn -^а^ро(_О)

+ |(4п + 3)).

Константа Q_n зависит от величины донного давления: Р_е — Ро + а_пР_п, которое можно задавать на конце пластинки (ж — 1). Давление, при котором «_п — 0, будем называть автомодельным давлением Р_а, так как в этом случае профиль скорости п(е) не меняется вдоль пластинки. Интерес представляют случаи задания донных давлений, отличных от автомодельного.

На рис. 6 представлены профили скорости в пограничном слое в сечениях ж — 0 ^ 0.6, 0.8,1.0 вдоль пластинки для случая S_w — 0.75, 7 — 1.4, Р_е — 0.5Р_а при вдуве газа с коэффициентом массообмена к — 0.1. В случае разгона потока (Р_е< Ра) скорость в пограничном слое в окрестности задней кромки локально превышает скорость набегающего потока.

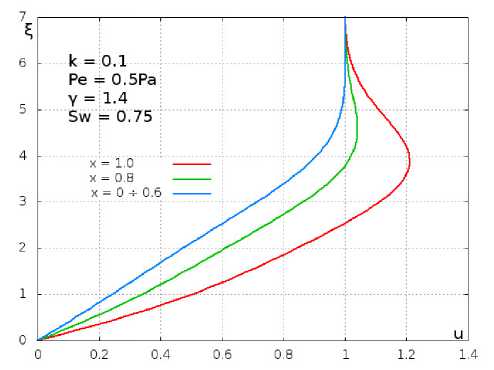
Рис. 6. Профили скорости в нескольких сечениях пластины по ж в пограничном слое на режиме вдува ( к — 0.1) в случае разгона потока (Р_е — Р_а/2); 7 — 1.4, S _w — 0.75

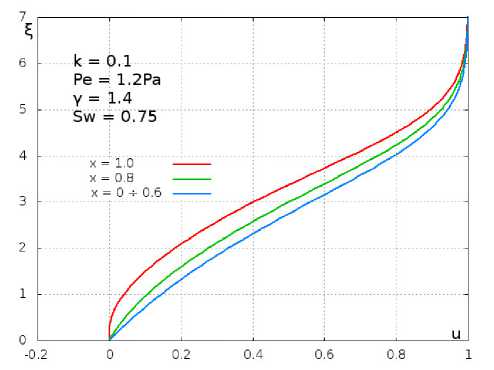
Рис. 7. Профили скорости в нескольких сечениях пластины по ж в пограничном слое на режиме вдува ( к — 0.1) в случае торможения потока (Р_е — 1 . 2 Р_а); 7 — 1 . 4, S_W — 0.75

На рис. 7 представлены профили скорости в пограничном слое в сечениях ж = 0 А 0.6, 0.8,1.0 вдоль пластинки для случая S_w = 0.75, у = 1.4, Р_е = 1.2Р_а при вдуве газа с коэффициентом массообмена к = 0.1. В данном случае наблюдается торможение потока в окрестности поверхности пластины.

В рассматриваемом случае торможения потока ( Р_е > Р^ давление и коэффициент вду-ва газа подобраны таким образом, чтобы наблюдать на задней кромке начало явления отсоединения пограничного слоя (рис. 7). При дальнейшем увеличении донного давления отсоединение будет распространяться по пластинке в направлении передней кромки. Важно отметить, что, как только на задней кромке появляется отрыв, решение во всей рассматриваемой области 2 (рис. 1) перестает удовлетворять выведенной системе уравнений (11), (12), (19), (20) и (21) в силу появления невязкого подслоя на пластинке [6]. Следовательно, в данной постановке исследовать задачу при больших донных давлениях не представляется возможным.

7.    Выводы

В данной работе проведено исследование двумерной задачи обтекания плоской пластины гиперзвуковым потоком вязкого газа при наличии массообмена на поверхности и вязкого взаимодействия между пограничным слоем и внешней невязкой областью течения. С помощью гиперзвуковой теории малых возмущений выведена система уравнений для невязкой области течения в предположении, что форма ударной волны отличается от автомодельной и зависит от значения собственного числа. Выведена система уравнений пограничного слоя при наличии массообмена на поверхности пластины, также содержащая собственное число. Из анализа граничных условий, связанных с массообменном на поверхности, получен общий вид зависимости для автомодельной скорости вдува газа. Из условия сращивания решений для давления и нормальной компоненты скорости на внешней границе пограничного слоя получено интегральное соотношение для определения собственного числа. Установлено, что решение краевой задачи в окрестности передней кромки не является единственным, а имеет однопараметрическое семейство решений. Численно найдена зависимость собственного числа краевой задачи от определяющих параметров. Показано, что увеличение скорости вдува приводит к существенному уменьшению собственных чисел. Установлено, что при отсосе газа через поверхность пластины максимум профиля возмущения энтальпии смещается в нижнюю часть пограничного слоя, а при вдуве газа - он располагается в центральной части пограничного слоя.

Работа выполнена при поддержке гранта РФФИ (проект №13-01-00202).