Обзор методов оценки коэффициентов жесткости и демпфирования опор скольжения

Подшипники скольжения нашли широкое применение в различных вращающихся машинах, таких как турбины, центробежные насосы, турбонагнетатели и т. д. В частности, их массовое использование имеет место в системах турбонаддува автомобильных, железнодорожных, судовых двигателей [1, 2] . Развитие данной отрасли машиностроения привело к тому, что газотурбинный наддув стал неотъемлемой структурной единицей двигателя внутреннего сгорания, которая в значительной степени определяет его эффективность и качество. Условия работы турбокомпрессора, как правило, включают широкий диапазон частоты вращения ротора и длительный ресурс (десятки тысяч часов) [3] . В связи с этим эксплуатационная надежность является одним из главных требований, предъявляемых к системам турбонаддува. Основным критерием, определяющим работоспособность любого турбокомпрессора, является устойчивое вращение ротора в течение заданного ресурса. На стадии проектирования и разработки надежность работы роторного узла на опорах скольжения оценивается посредством исследования устойчивости движения. Такая оценка предполагает решение задачи движения ротора c учетом гидродинамической силы, возникающей в подшипнике скольжения. При этом гидродинамическая сила может быть учтена как явно, так и неявно – в виде коэффициентов жесткости и демпфирования. Последнее положение относится к области линейной роторной динамики [4] , задачами которой являются нахождение критических скоростей и оценка амплитуд вынужденных колебаний.

Оценка стабильности работы ротора турбокомпрессора должна быть выполнена еще на стадии проектирования с учетом характеристик опор. В современной инженерной практике доступный функционал для анализа динамики ротора на опорах скольжения ограничен и, как правило, требует предварительного знания коэффициентов жесткости и демпфирования. Основной целью данной статьи является обзор методов оценки динамических характеристик подшипников скольжения, которые применяются в качестве опор современных турбокомпрессоров.

Методы исследования

Типичная конструкция ротора турбокомпрессора включает (рис. 1): вал 1, колесо компрессора 2, колесо турбины 3, радиальные подшипники скольжения 4, упорный подшипник 5. Радиальные подшипники скольжения могут быть представлены различными конфигурациями. В малоразмерных и высокооборотных турбокомпрессорах обычно используются подшипники с плавающей втулкой (см. рис. 1), или моновтулкой, имеющие два смазочных слоя.

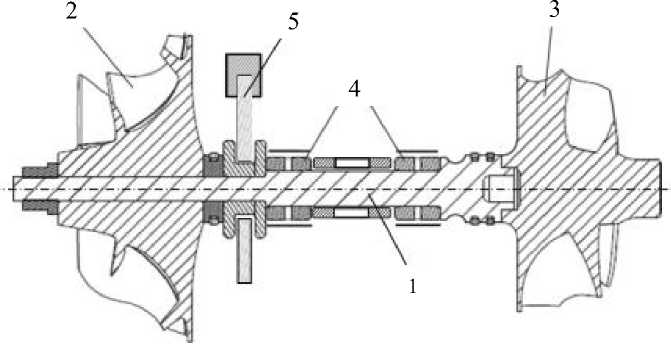
Рис. 1. Поперечный разрез ротора малоразмерного автомобильного турбокомпрессора Fig. 1. Cross-section of a small automotive turbocharger rotor

В инженерной практике на стадии разработки и проектирования такого роторного узла методы решения задач роторной динамики ограничены доступными инструментами для анализа. Преимущественно одним из доступных является метод конечных элементов (МКЭ), реализованный, как правило, посредством коммерческих программных комплексов. Уравнение движения для вращающегося тела при решении МКЭ представляется в матричной форме и в общем виде записывается следующим образом [5] :

[М]{q} + ([С] + [С_ь]) • { q} + ([К] + [ВД • к) = Ш (1) где {q} - вектор перемещения, {q} - вектор скорости, {q} - вектор ускорения, [М] - матрица масс, [С] - общая матрица демпфирования (включающая гироскопическую матрицу и матрицу демпфирования опор [С_ь]), [К] - общая матрица жесткости (включающая матрицу жесткости опор [К_ъ]), {Л - вектор внешней силы.

Входящие в уравнение (1) матрицы жесткости и демпфирования опор являются исходными данными при формировании расчетной модели, элементы который должны быть известны заранее. Данные матрицы составляются в соответствии с принятым способом представления опоры. Как правило, радиальный подшипник схематизируется пружинами и демпферами, как показано на рис. 2. Матрицы жесткости и демпфирования содержат по 4 элемента:

к_л,уЛ гСгт с_Л,г1

[К] = хх ух , [ Сь] = |си сух], (2) iK-xy Куу] L сху суу\ где кхх, Ууу, ХххУУу - прямые коэффициенты жесткости и демпфирования; куу , Ухх, хуу, Ухх -перекрестные (диагональные) коэффициенты жесткости и демпфирования.

Коэффициенты жесткости и демпфирования называются динамическими характеристиками [6] , которые для подшипника скольжения представляют собой частные производные проекций гидродинамической силы F (рис. 3) по соответствующим направлениям [7, 8] :

,                  t                 t                        .dFy xx =    ,      yy =    ,      xy =    ,      yx =    ;

_ dFx        _ dFy        _ dFx        _ dFy cxx = ̇, cyy =   ̇, cxy = ̇, cyx =   ̇ , где Fx , Fy – проекции гидродинамической силы на соответствующие оси координат.

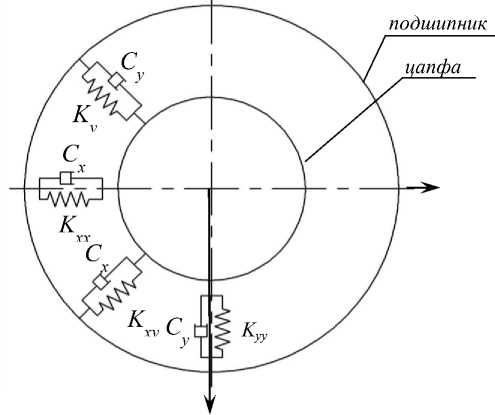
Рис. 2. Схематизация динамической системы ротор – подшипник с пружинами и демпферами Fig. 2. Schematic representation of the rotor – bearing dynamic system with springs and dampers

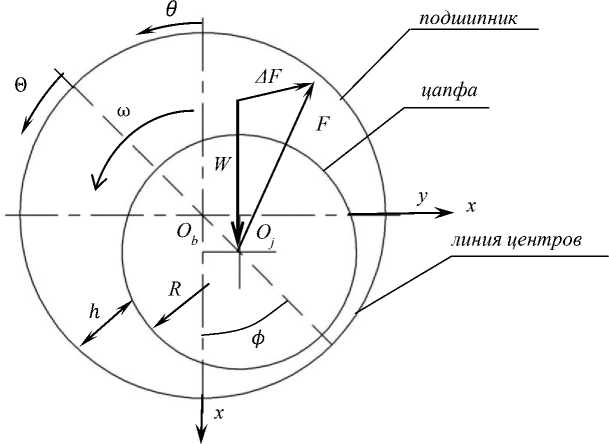
Рис. 3. Сечение цилиндрического подшипника скольжения

Fig. 3. Section of cylindrical plain bearing

Гидродинамическая сила F является равнодействующей давления p , создаваемого смазочным слоем:

L

F =- ^R П^p ∙ dddz ,                                                  (4)

где L – осевая длина подшипника, ^1 , 02 – начальный и конечный углы приложения давления (зависят от принятых граничных условий).

Распределение давления p в тонком смазочном слое, в свою очередь, является результатом решения уравнения Рейнольдса, которое для идеального цилиндрического подшипника скольжения, смазываемого несжимаемой жидкостью, в цилиндрической системе координат имеет вид

1 д    ℎ ³ др ( z , 9 )

№д9\ 12∙ р дв )

д

+

ℎ³ др ( z , 9 )

12∙ р dz

1 д ℎ д ℎ =₂ ^Шд9 ^{+  ,}

где р – динамическая (абсолютная вязкость), ш – угловая скорость , h – толщина смазочного слоя, t – время. Таким образом, оценка динамических характеристик подшипника скольжения невозможна без решения основного уравнения гидродинамической теории смазки.

Возникающая при движении цапфы в пространстве зазора поддерживающая сила F имеет нелинейный характер изменения в зависимости от перемещений [5, 9] . При движении ротора коэффициенты жесткости и демпфирования опор являются коэффициентами, отражающими изменение этой силы смазочного слоя в зависимости от перемещений шипа в опоре. Такое представление называется линеаризацией силы, а уравнение движения (1), где гидродинамическая сила учитывается данным образом, называется линеаризованным:

Fx

=

∙ X + ^Fxy

^∙ У + ^схх ∙ ̇+ ^сху

∙J̇, ^F_y =     ∙ У + кух ∙ X +с УУ ∙J̇+с ух ∙ ̇ .

В настоящее время общепринятым считается подход, когда динамические характеристики подшипников определяются на основании предположения прецессии ротора относительно положения статического равновесия (линеаризация относительно точки статического равновесия). При движении цапфы, нагруженной силой W в пространстве зазора подшипника, возникает гидродинамическая сила F (см. рис. 3) Вектор силы F имеет постоянную составляющую ^Fo , обусловленную постоянно действующей нагрузкой, и переменную (дополнительную) Δ :

F =  +Δ F .

Постоянная составляющая силы ^Fo имеет место в точке статического равновесия, где выполняется следующее условие:

=

Fxo\

Fyo)

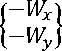
В данном случае динамические характеристики выражают зависимость дополнительной гидродинамической силы Δ F при смещениях цапфы от точки статического равновесия на величины Δ X ,Δ У ,Δ у ̇,Δ у ̇ . Cилы Δ ^Fx и Δ F , действующие на цапфу, при этом определяются с помощью линеаризации в положении равновесия разложением в ряд Тэйлора первого порядка:

= +Δ ^ = ⁺ o₀ ∙∆¹⁺ ®„ ∙∆ у ⁺ (S ̇0»∙∆ ̇+(^ _̇ К ∙∆ ^̇= (9) ^FXO + ^xx ∙∆ X + ^Fxy ∙∆ У +с XX ∙∆ ̇+с xy ∙∆J̇.

=   +Δ Fy =   ⁺ (^)o ∙∆ У ⁺ O₀ ∙∆¹⁺̇o.∙∆ ̇+̇o„∙∆ ̇=

^FyO + ^Fyy ∙∆ У + ^Fyx ∙∆ X +с УУ ∙∆J̇+с yx ∙∆ у ̇.

Величины Δ X ,Δ У ,Δ5̇,Δ у ̇ в такой постановке задачи являются бесконечно малыми. При движении шейки вала вокруг положения равновесия координаты центра цапфы вала изменяются на Δ X , У , возникает дополнительное давление Δ P . При этом с использованием разложения Тэйлора первого порядка «возмущенное» гидродинамическое давление и толщина смазочного слоя составляют (рис. 4)

P =  +Δ P =  ⁺О^Δ X ⁺ (I) ^Δ У ⁺ġ Δ ̇+ġ Δ ̇=

0       x°У/ о

=   + Px ∙∆ X + Ру ∙∆ У + Рз ̇∙∆ ̇+ Pi ̇^∙∆J̇,

ℎ= с + X ∙ cos9 + У ∙ sin9 = ℎ₀ +∆ х ∙ cos9 + ∆ У ∙ sin9 .

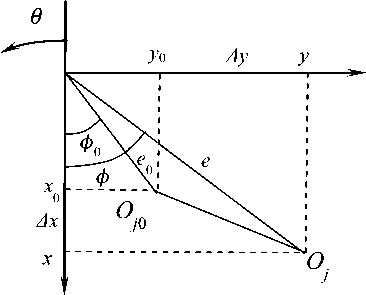
Рис. 4. Положение центра цапфы в статическом равновесии и при отклонении

Fig. 4. Position of the center of the journal in static equilibrium and during deflection

Подстановка значений (11), (12) в уравнение (5) преобразует последнее в систему пяти дифференциальных уравнений, решение которых позволяет получить «возмущенное» давление:

1 д №дв	ℎ 1^ + 12 /я дв + a) d ℎо	д ℎn dv,-     \		(13)
		+ dz 12 p	+ 91  =0, i =0,∆л,∆ у ,∆ ̇,∆ ̇, dz     J
/о =	2      , ℎо dp0 1	cos в ,	во =0, ℎо dp0\	(14)
f ∆ =	- — Ш 4 p дв 2 ℎо dp0 1		9∆ X = 4 p dz) соs 9, ℎ0 dp0\ . Л	(15)
/∆ =	- — 0) 4 p дв 2	sin в ,	9∆ У = 4 p дв ) sin 0,	(16)
f ∆ a ̇=	-соѕ в ,		9 ∆а̇=0,	(17)
/∆ j ̇=	-sin в ,		9 ∆ a ̇=0․	(18)

Коэффициенты жесткости в форме уравнений линеаризованной силы (9), (10) являются интегральными значениями «возмущенного» давления:

		L 2 02					L 2 02
=	- R	и _L 01 2	P ∆ X ∙	cos в dddz	=	- R	П _L 01 2	P ∆ X ∙	sin в dddz	(19)
		L 2 02					L 2 02
=	- R	П _L 01 2	p ∆ X	∙cos в dddz	=	- R	и _L 01 2	p ∆ X	∙sin в dddz	(20)

Аналогично вычисляются коэффициенты демпфирования. В теории дифференциальных уравнений данный метод решения носит название решения по малому параметру или метод малых возмущений [10]. Классическое описание определения динамических характеристик подшипников скольжения с использованием данного подхода представлено в работе [11]. Полученные таким образом коэффициенты жесткости и демпфирования рекомендованы стандартами API RP 684 [12] и ISO TS 31657-1: 2020 [13] для использования в задачах роторной динамики. Принцип линеаризации гидродинамической силы в точке статического равновесия положен в основу коммерческих расчетных программ, которые могут быть использованы для получения коэффициентов жесткости и демпфирования. Их краткое описание будет представлено далее.

Dyrobes ( Dynamics of Rotor-Bearing System ) [14] представили программный комплекс, разработанный для решения задач роторной динамики. Комплекс имеет встроенный модуль BePerf [15] ( Bearing Performance ) для анализа статических и динамических характеристик подшипников скольжения (в том числе и на газовой смазке). В комплексе Dyrobes Beperf доступны для анализа следующие типы подшипников: цилиндрические ( plain journal bearing ), клиновые ( fixed-lobe bearing ), подшипник с самоустанавливающимися сегментами (titling pad bearing), подшипник с плавающей втулкой ( floating ring bearing ) и др. (рис. 5).

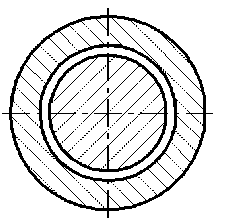
Цилиндрический подшипник ( plain journal bearing )

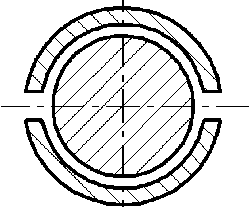
Подшипник с осевыми канавками ( axial grooved )

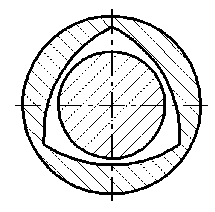
Клиновой подшипник ( fixed-lobe bearing)

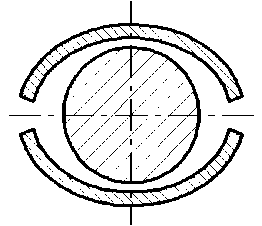
Двуцентровой или эллиптический подшипник

Elliptical (Lemon) bearing

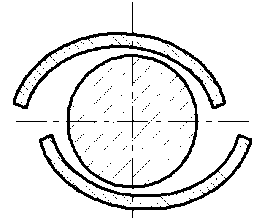
Подшипник со смещенными вкладышами

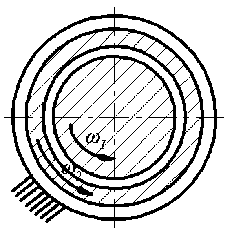
Подшипник с плавающей втулкой ( floating ring bearing )

Рис. 5. Основные типы подшипников, доступные для анализа [15]

Fig. 5. Main types of bearings available for analysis [15]

Статические характеристики подшипников определяются в положении равновесия Dyrobes Beperf , когда внешняя нагрузка уравновешена давлением смазки. При этом распределение давления определяется решением уравнения Рейнольдса в положении стационарного равновесия (производные по времени равны нулю) [16]:

=

̅                        ̅                                                                                                                                                                                       ̅, где ̅= ∙ , – осевая координата, = ∙ – окружная скорость.

Данное уравнение дополнено коэффициентами турбулентности потока в окружном и осевом направлениях ̅, (предложенные Константинеску [17]), которые для турбулентного потока равны

1 =12+0,0136∙   ․

̅

1 =12+0,00043∙   ․ ,

^у где = ∙ ∙ – число Рейнольдса. Для ламинарного течения ̅= = 1/12․ Динамические характеристики определяются методом линеаризации гидродинамического давления в окрестности положения равновесия (разложением в ряд Тейлора первого порядка).

DynamicsR4 [18] программный продукт ООО «Альфа-Транзит», который разработан для решения широкого круга линейных и нелинейных задач роторной динамики. Имеет встроенный модуль DynFB, разработанный для расчета статических и динамических характеристик подшипников скольжения [19, 20], подход к оценке последних аналогичен Dyrobes Beperf. Математическая модель гидродинамической смазки подшипника скольжения также основана на уравнении Рейнольдса (решается методом конечных разностей), модифицированном в соответствии с моделью турбулентности Константинеску, и уравнении сохранения энергии для течения жидкости в тонких пленках.

Аналогичный Dyrobes, DinamicsR4 подход к определению коэффициентов жесткости и демпфирования реализован в программном комплексе COMSOL : модуль роторной динамики [21]. Программный продукт Ansys Mechanical содержит элемент FLUID 218 для оценки динамических характеристик подшипника скольжения в заданном пользователем положении равновесия [22].

Произвести анализ характеристик подшипника скольжения возможно, используя программный комплекс Amesim , который позволяет моделировать и анализировать процессы в мультидис-циплинарных системах. Amesim содержит библиотеку Hydraulic Resistance c встроенной моделью цилиндрического подшипника скольжения. Математическая модель расчета характеристик подшипника в Amesim основана на методе подвижности [23], не требующем решения уравнения Рейнольдса, когда эксцентриситет вала определяется дифференциальным уравнением:

f?^

dt цЫ)

• М + ы • е,

где М - вектор подвижности, компоненты которого являются функцией эксцентриситета и размера подшипника М = М(е; Ь/D'). В зависимости от отношения длины подшипника к его диаметру доступны три типа решения Ocvirk (Ь/D <  1/8), Goenka (1/4< L/D <1), Warner-Sommerfeld (Ь/D >1) [24, 25]. Определение динамических характеристик возможно после вычисления положений вала для разных величин и направлений внешней нагрузки с использованием пересчета.

Анализ методов

Линеаризация гидродинамических сил в положении статического равновесия является доминирующим подходом для вычисления коэффициентов жесткости и демпфирования. Такой вывод можно сделать на основании данных таблицы, где в краткой форме изложены способы учета характеристик опор скольжения [26-47]. В работе [26] данный метод используется для оценки динамических характеристик цилиндрического подшипника с учетом непараллельности осей цапфы и корпуса. Метод линеаризации сил может быть применен для подшипника скольжения любой конфигурации, если для него возможно составить и решить систему уравнений, аналогичную (13)-(18): в положении статического равновесия и в возмущенном состоянии [27, 38, 40, 46]. В исследовании [27] оцениваются динамические параметры текстурированного подшипника с помощью данного метода, в [38] - для двухслойного подшипника с плавающей втулкой, в [46] -для трехклинового и эллиптического.

Линеаризация силы методом разложения в ряд Тэйлора возможна с учетом членов ряда высших порядков малости. Коэффициенты демпфирования и жесткости, полученные таким способом, называются динамическими характеристиками второго и третьего порядка. Алгоритм вычисления коэффициентов второго и третьего порядка для идеального цилиндрического подшипника скольжения представлен в работах [32-34], где проведено сравнение их с коэффициентами первого порядка.

Аналитические подходы к определению коэффициентов жесткости и демпфирования также не теряют своей актуальности. В работе [28] представлен способ расчета динамических характеристик цилиндрического подшипника скольжения с относительной длиной от 0,5 до 2,0 на основании полиномиальной аппроксимации точных решений для короткого, длинного подшипника и решения Нгуена - Шафера [48]. Скорректированные характеристики сравнивались с характеристиками, полученными в результате решения уравнения Рейнольдса методом конечных разностей. Полиномиальная аппроксимация аналитических решений для динамических характеристик получила дальнейшее развитие применительно к подшипникам с плавающей втулкой [30]. Однако сравнение результатов анализа моделирования разгона ротора с аппроксимированными значе- ниями коэффициентов и нелинейными силами (полученными при решении уравнения Рейнольдса на каждом шаге интегрирования) привело больше к качественному совпадению. Несмотря на недостатки, самостоятельно отмеченные авторами исследования [30], теория короткого подшипника применяется и далее при анализе динамики ротора на подшипниках с плавающей втулкой [31]. Также для подшипников с двумя смазочными слоями коэффициенты жесткости могут быть эквивалентными как для двух слоев сразу [38], так и отдельными для каждого слоя [36, 37], последний подход является предпочтительным на основании результатов исследования [28].

Сравнительный анализ методов оценки динамических характеристик подшипников скольжения Comparative analysis of methods for assessing the dynamic characteristics of plain bearings

Автор	Тип подшипника	Предлагаемый метод оценки динамических характеристик	Учет влияния специальных факторов
X. Sun, K.K. Sepahvand (2021) [26]	Идеальный цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка	Учитывается перекос вала относительно подшипника
L Smolik, J. Rendl, M. Omasta, M. Byrtus и др. [27]	Текстурированный цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка
S. Dyk, J. Rendl, M. Byrtus, L. Smolık (2018) [28]	Идеальный гладкий цилиндрический	Коэффициенты, рассчитанные по теории короткого подшипника, решения Нгуена – Шаффера, полиномиальная коррекция аналитических решений
L. Smolík, J. Rendl, S. Dyk, P. Polach, M. Hajzman (2018) [29]	Идеальный гладкий цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка	–
S. Dyk, L. Smolík, J. Rendl (2018) [30]	Подшипник с плавающей втулкой, идеальные гладкие поверхности	Коэффициенты, рассчитанные по теории короткого подшипника. Рассмотрено 9 типов линеаризации гидродинамических сил	Учет массы и скорости плавающей втулки
L. Smolík (2023) [31]	Подшипник с плавающей втулкой, идеальными гладкими поверхностями, внутренний и внешний слой сообщаются через единственное отверстие	Коэффициенты жесткости, полученные с использованием теории короткого подшипника
H. Sayed, T.A. El-Sayed (2022) [32]	Идеальный гладкий цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 2-го порядка	Учитывается влияние корпуса подшипника (масса на пружинах)
O. Ahmed, T.A. El-Sayed, H. Sayed (2023) [33]	Идеальный гладкий цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 2-го порядка	Учитывается влияние корпуса подшипника (масса на пружинах)

Продолжение таблицы Table (Cont.)

Автор	Тип подшипника	Предлагаемый метод оценки динамических характеристик	Учет влияния специальных факторов
H. Sayed, T.A. El-Sayed (2022) [34]	Идеальный гладкий цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 3-го порядка
T.A. El-Sayed, M.I. Friswell, H. Sayed (2022) [35]	Идеальный цилиндрический подшипник скольжения	Коэффициенты демпфирования учитываются линеаризацией силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка
Y. Zhang, W. Wang, D. Wei, G. Wang, J. Xu, K. Liu (2022) [36]	Подшипник с плавающей втулкой, слои сообщаются между собой через 4 отверстия	Радиальные и тангенциальные коэффициенты, вычисленные как частные производные гидродинамической силы в положении равновесия	Учитываются изменения толщины смазочного слоя за счет температурных деформаций. Тип смазки – неньютоновская. Масса кольца учитывается
Y. Zhang, W. Wang , D. Wei, и др. (2022) [37]	Подшипник с плавающей втулкой, слои сообщаются между собой через 4 отверстия	Радиальные и тангенциальные коэффициенты, вычисленные как частные производные в положении равновесия	Учитываются изменения толщины смазочного слоя вследствие температурных деформаций. Тип смазки – неньютоновская. Масса кольца учитывается
Z. Xie, W. Zhu (2022) [38]	Подшипник с плавающей втулкой	Коэффициенты жесткости, полученные линеаризацией силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка с вычислением эквивалентного коэффициента жесткости для двух слоев	Учет шероховатости поверхности, учет температурного режима смазочного слоя
C. Chen, J. Jing, J. Cong, Z. Dai (2018) [39]	Цилиндрический подшипник с двумя осевыми канавками	Оценка динамических коэффициентов на основании двух расчетов: статического расчета и гармонического отклика на дисбаланс
H.U. Jamali, H.S. Sultan (2023) [40]	Цилиндрический подшипник с разными формами фаски	Коэффициенты жесткости получены линеаризацией в положении статического равновесия разложением в ряд Тейлора 1-го порядка	Перекос вала в подшипнике (жесткий ротор)
A. Wang, Y. Bi, X. Cheng (2022) [41]	Цилиндрический	Коэффициенты жесткости и демпфирования оцениваются на основании метода непрерывного динамического анализа, который предлагается для применения в ходе эксплуатации роторного узла

Окончание таблицы

Table (End)

Автор	Тип подшипника	Предлагаемый метод оценки динамических характеристик	Учет влияния специальных факторов
R. Reddy, M.J. Srinivas (2022) [42]	Подшипник с плавающей втулкой	Поиск коэффициентов подшипника производится на основании алгоритма роевой оптимизации, где целевой функцией выступает погрешность определения амплитуд с линеаризованными коэффициентами и силами по теории короткого подшипника
J. Yang, R. Zhu, H.P. Lee (2022) [43]	Цилиндрический	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка	Учет шероховатости поверхности шипа и подшипника
M.I. Sadiq, W. Aizon, W. Ghopa, M.Z. Nuawi, M.R. Rasani, N.K. Khamis, M.R.A. Mansor [44]	Цилиндрический	Аналитическое извлечение коэффициентов демпфирования и жесткости выполняется на основе экспериментальных данных динамической вязкости при различных температурах	В работе биомасла (рапсовое, пальмовое олеиновое и соевое) оцениваются с точки зрения их динамических характеристик по сравнению с минеральным смазочным материалом SAE40 для подшипников скольжения.
L. Zhang, X. Zhang, H. Xu [45]	Радиальный	Изменение жесткости и коэффициента демпфирования масляной пленки достигается методом регулировки зазора	Регулировка радиального зазора реализуется через механический передаточный механизм
L. Zhang, X. Zhang, H. Xu (2022) [45]	Эллиптический подшипник с регулируемым радиальным зазором	Коэффициенты жесткости и демпфирования, полученные по теории короткого подшипника
C.A.A. Viana, D.S. Alves, T.H. Machad (2022) [46]	Эллиптический и трехклиновой	Линеаризация гидродинамической силы в положении статического равновесия разложением в ряд Тейлора 1-го порядка
D. Pérez-Vigueras, J. Colín-Ocampo, A. Blanco-Ortega, R. Campos-Amezcua и др. (2023) [47]	Цилиндрический	Коэффициенты жесткости оцениваются методами вычислительной гидродинамики (Computational Fluid Dynamic) с использованием алгоритма интеграции жидкой среды и твердого тела (Fluid Structure interaction)

В целом аналитические выражения коэффициентов жесткости и демпфирования предоставляют очевидное преимущество в виде низких вычислительных затрат, которые актуальны, например, на стадии прикидочных расчетов, как в работе [44]. Также готовые решения позволяют использовать алгоритмы оптимизации, как в [42], где описывается теория короткого подшипника для опоры с плавающей втулкой. Однако такие аналитические решения не всегда адекватно отражают динамические свойства смазочного слоя, на что указано авторами в работе [30] применительно именно к подшипнику с плавающей втулкой. Стоит отметить тенденцию современных ученых к попыткам разработать «непрерывную расчетную модель» с помощью формирования базы данных значений динамических коэффициентов [35], которую можно связать с анализом движения ротора, что позволяет снизить вычислительные затраты.

Также для оценки динамических характеристик используются методы вычислительной гидродинамики ( CFD ) с применением интерфейса интеграции жидкой среды и твердого тела ( FSI – Fluid Solid Interaction ) в нестационарной постановке. В обзоре [47] приведен пример анализа цилиндрического подшипника скольжения в Ansys Fluent, где изменение положения вала и геометрии смазочного слоя производится с помощью алгоритма перестраивающихся сеток, а коэффициенты жесткости вычисляются с применением пользовательских функций. Данный подход имеет крайне высокие вычислительные затраты, хотя его возможно применить к любому типу подшипника скольжения.

Выводы

Оценка характеристик жесткости и демпфирования подшипников скольжения является, несомненно, актуальной задачей, которая решается многими современными учеными и техническими специалистами по-разному. На основании произведенного обзора современных исследований в данной области можно сделать следующие выводы:

• -    объектом изучения большинства работ по оценке динамических характеристик становятся идеальные цилиндрические подшипники, которые имеют один смазочный слой;

• -    основным методом оценки динамических характеристик подшипников скольжения являются готовые аналитические зависимости и линеаризация гидродинамической силы в положении статического равновесия (метод реализован в коммерческих программных комплексах);

• -    аналитические решения для оценки коэффициентов жесткости и демпфирования подшипников с несколькими смазочными слоями (конструкция, аналогичная представленной на рис. 1), основанные на теории короткого подшипника, при дальнейшем использовании в задачах роторной динамики дают лишь качественное совпадение с нестационарным нелинейным расчетом;

• -    в современных исследованиях по оценке динамических коэффициентов не рассматривается конструкция с плавающей/качающейся моновтулкой;

• -    представленные исследования не отражают влияния особенностей конструкции подшипника, таких как канавки, технологические отверстия, на коэффициенты жесткости;

• -    для подшипника с плавающей втулкой (и моновтулкой) непроработанными остаются вопросы влияния теплового расширения и изгиба вала (вызывающего поворот плавающей втулки) на гидродинамическую силу и ее коэффициенты;

• -    в работе [41] отмечен факт изменения жесткости подшипникового узла в ходе эксплуатации вследствие износа, что является возможным направлением в анализе и прогнозировании характеристик жесткости и демпфирования;

• -    недостаточно разъясненным остается подход к оценке характеристик жесткости и демпфирования подшипников на основании нестационарного нелинейного расчета, который по сути является обратной задачей, но бывает необходим.

Несмотря на тот факт, что общепринятым подходом к оценке динамических характеристик подшипников скольжения является линеаризация в положении статического равновесия, рекомендации к их использованию в анализе динамики ротора всегда включают примечания, общая суть которых сводится к границам применяемости данной теории. Стандарт API RP 584 [11] обращает внимание, что линеаризованные коэффициенты используются для описания движения с малыми амплитудами относительно стационарного положения равновесия и при перемещениях вала, составляющих 80 % от зазора, возникают нелинейные эффекты, которые могут быть значительными. В [10] приведено более жесткое ограничение по амплитудам движения – не выше 50 % от зазора. Похожие примечания можно найти в [4, 5, 9, 30] и др.

Современные турбокомпрессоры даже при работе на стационарных режимах могут подвергаться ударным нагрузкам, вибрациям с большими амплитудами, которые неизбежно влекут за собой большие отклонения ротора, не соответствующие предположению малых орбит вокруг положения равновесия. Данное обстоятельство ставит вопрос о ином подходе к определению коэффициентов жесткости, который может быть основан на комбинации линеаризации силы в положении равновесия и дополнительной математической моделью, описывающей область больших смещений, которая будет коррелировать с результатами нелинейного анализа.