Оценивание параметров динамической стохастической модели общего равновесия экономики Казахстана на основе байесовского подхода

Современное государственное управление требует строгой количественной оценки соци- ально-экономических эффектов от принимаемых решений, количественного обоснования их оптимальности. «Политические решения могут быть простыми, но модели не могут и не должны быть слишком простыми» [1, с. xiii]. Развитие модельного ап- парата, численных методов, компьютерных технологий позволило использовать в экспертной работе сложные динамические модели. На сегодняшний день базовым инструментом макроэкономического анализа и моделирования, а также стандартным инструментом для разработки экономической политики стали DSGE-модели. Отметим, что их основными характеристиками являются:

• -    вывод макроэкономических соотношений из микроэкономических поведенческих моделей и использование теории рациональных ожиданий при описании поведения домашних хозяйств и предприятий реального сектора;

• -    опора на неокейнсианские положения об институциональных «провалах рынка» (несовершенная конкуренция и жесткие цены), что кажется особенно актуальным для постсоветских экономик, в

которых развитие рыночных отношений еще не достигло уровня западных стран;

• -    положение, что монетарная политика вызывает лишь краткосрочные отклонения от долгосрочного равновесия, которое в простейшем случае может быть определено с помощью фильтра Ходрика – Прескотта;

• -    отказ от традиционного эконометрического оценивания в пользу калибрации параметров микроэкономического поведения. В последнее время калибрация стала дополняться байесовским оцениванием.

На сегодняшний день известно не так много вариантов DSGE-моделирования Казахстана. В работах [2–4] параметры модели не оцениваются на статистических данных, а калибруются. Модель Национального банка Казахстана [5] не опирается на теоретический микрофундамент и является сугубо прикладной.

По сравнению с предыдущим нашим исследованием [6] мы расширили перечень моделируемых переменных, обобщили функцию полезности домашних хозяйств, а также провели строгое доказательство полученных результатов на основе метода Ла- гранжа.

Методология исследования

Ниже представлена малая DSGE-модель Казахстана, описывающая поведение ние проводятся сценарные расчеты, в том числе оцениваются эффекты от изменения процентной ставки в условиях инфляционного таргетирования.

Предположим, что домашние хозяйства имеют функцию полезности CRRA (с постоянной склонностью к риску) и максимизируют ожидаемую суммарную дисконтированную полезность: U = = Efe₀W—-Ф^ + Ф^^)] ^max t-OH ^-^     1+<р      1-1^

при бюджетном ограничении для t > 1 :

P_tC_t + M_t + D_t = W_tL_t + +M_t -i + (1 + R_t -i )D_t -i , где Яр] - оператор рациональных ожиданий¹; ft 6 (0; 1) - норма дисконтирования; C_t - потребление товаров и услуг при уровне цен P_t ; L_t - предложение труда по ставке заработной платы W_t ; M_t - номи-

M_t нальныи запас наличных денег, а m _t = -— реальные денежные остатки; D_t - сбережения (депозиты) домашних хозяйств в активах, приносящих процентный доход по ставке R_t на момент времени t .

В функции полезности предполагается, что она положительно зависит от реального потребления и запаса денег2 и отрицательно – от затрат труда.

В бюджетном ограничении предполагается, что домашние хозяйства могут свободно сберегать и кредитовать, т. е. нет ограничений на заимствования. Таким образом, переменная Dt отражает не все де- домашних хозяйств, предприятий реально- го сектора и денежного регулятора, а также их взаимодействие в ситуации равновесия. Модель предназначена для описания экономики в краткосрочном периоде. Соответственно, номинальные показатели характеризуются значительной инерционностью, а основной капитал принимается как заданный. Последнее означает, что инвестиции явно не выделяются. Также предполагаются заданными фискальные параметры и внешнеэкономический фон – их влияние задается экзогенными случайными возмущениями.

Параметры модели оцениваются с помощью байесовского оценивания, откалиброванные значения параметров используются в качестве априорных. В заключе-

• ¹    Под рациональным понимается такое поведение экономических агентов, что вся доступная информация и имеющийся опыт используются настолько эффективно, что ожидаемое значение будущих переменных отклоняется от фактического лишь случайно. Иными словами, E[z_t+1] = z_t+1 + £_t+1, где £ - белый шум [2].

• ²    Следует сказать несколько слов о включении денег в функцию полезности. Если сбережения приносят процентный доход и благодаря этому увеличивают будущее потребление, то наличные деньги доход не приносят, а лишь обесцениваются инфляцией. Соответственно, невключение их в функцию полезности приводит к тому, что оптимальный запас наличности должен быть равен 0, что противоречит реальной жизни. Чтобы этого избежать, зачастую деньги включают в функцию полезности. Против этого высказывается возражение, что деньги сами по себе не составляют благосостояние, но лишь косвенно способствуют этому, экономя время на совершение сделок и, следовательно, уменьшая трансакционные издержки.

позиты домашних хозяйств, а только чистые активы. Также явно не выделяются налоговые платежи и трансферты от государства.

Бюджетное ограничение домашних хозяйств может быть выражено через реальные (дефлированные) показатели: (1 + nt)(Ct + mt + dt) - (1 + nt)wtLt + +mt-i + (1 + Rt-i)dt-i, D где dt —  — реальные активы, приносящие

_          wt процентный доход; wt — -— реальная заработная плата; nt — —— 1 - уровень ин-pt-i фляции.

Лагранжиан рассматриваемой чи на условный экстремум имеет вид

от

1-1

t=0

' i^-a      L 1⁺^      m_t^i- ^

---Фз-^- — + Ф -

-а   1 + ^   1—ф\

-

зада-

⁽1 + n_t⁾⁽C_t + m_t + d_t) - ⁽1 + n_t⁾w_tL_t

-)]

.

-m_t —i

-

(1 + R_t -i )d_t -i

Условия первого порядка для потребления, реальных денежных остатков, предложения труда и депозитов равны (для упрощения записи мы опускаем оператор рациональных ожиданий для переменных в периоде t + 1 ):

д£ д£

-— - frWmt ^ dm_t

д£ дЦ

д£

^С— £ - (1+п-)-0^    ^t   —A t ;

^{(1 + n}t )

'-A_t(1 + n_t)+A_t+ i -0^ ^pt^m t^-^ -A_t(1+n_t)-A_t+ i ;

^^^^н

■ f^L* + A t (1 + n_t)w_t = 0 ^ ^ФЕ - = -A t (1 + n^w t ;

• -A t (1 + п - ) + A -+i (1 + R_t)-0^^ = ^At (1 + n_£)

(1+R t )'

Итоговые уравнения динамики переменных можно представить следующим образом.

Уравнение Эйлера для потребления:

(1 + E ^[ n t+i^])

(1 + Rt)   '

Функция спроса на деньги положительно зависит от расходов и отрицательно от ставки процента:

ym_t ~* - C — G—V)

^{t t} 1 + R_t

Функция предложения труда положительно зависит от реальной заработной платы:

Ф^ - - C -° w t .

Для анализа динамических свойств модели в терминах отклонений будем использовать логарифм отношения пере- менных к их равновесным значениям xt - \n^ - lnxt - Inx*.

Линеаризация уравнения Эйлера относительно равновесного состояния c^^

(1 + E ^[ n t ₊i])

(1 + R t )   .

При этом в рамках гипотезы рацио- нальных ожиданий предполагается, что экономические агенты имеют одинаковые и корректные представления о равновесном состоянии экономики, то есть E[C*] -- C*. Кроме того, в краткосрочном периоде это равновесное состояние стационарно.

Обозначив C_t - \п^ и прологарифмировав левую и правую части, получаем lnp - a(E[C t ₊i] - C t ) - E[n t ₊i] - R t .

Для вывода правой части IS-уравнения при условии низкой инфляции и ставки процента используется приближение ln(1 + x) ^ x.

Процентные переменные (инфляцию n_t и ставку процента R_t ) мы оставили без преобразований. Иногда их переписывают как отклонения от их равновесных значений (n_t - n_t - п * и R_t - R_t - R*). Тогда первое уравнение системы (IS-уравнение) становится однородным C t -E^ t+J + i CE^ t+J -R t ). Это легко показать, приняв во внимание, что в равновесии уравнение Эйлера имеет вид В - ^^ , то есть InB ~ п * - R* .

i+R *

Из этого также следует, что равновесная реальная ставка процента есть R* - п* - lnp. Если денежный регулятор поддерживает равновесную инфляцию на уровне таргета п * - п^т , то равновесная ставка процента должна быть равна R* - п^т - Infi (поскольку В Е (0; 1), lnP <0 и R * > п^т ).

Для линеаризации функции спроса на деньги и функции предложения труда использовались следующие формулы аппроксимации для малых отклонений x_t, y_t :

e^Xt~1 + x_t , E[ae^Xt] ~ a + aE[x_t], x_ty_t~0, x_t ~x * (1 + xt).

Функцию предложения труда можно аппроксимировать через равновесные состояния и отклонения следующим образом: Ф(Е*(1 + ^ = (c*(1 + Ct))-" w*(1 + Wt).

Принимая во внимание, что в равновесии функция предложения труда имеет вид ФЕ *® = C* ~^a w* , получаем (1 + Ы = (1 + ^(1 +w^.

Наконец, после логарифмирования получаем запись функции предложения труда через переменные отклонения: фЦ = -aCt + wt.

Воспользовавшись приближением x ? ~ x * (1 + ax_t~) и спросом на деньги в равновесии Фт '-^ C ' ⁷ = j^ , можно представить лог-линейное приближение для функции спроса на деньги:

-^mt+ aCt = (ТткИт+я*)'

Поскольку при низких ставках процента R t R ’ « 0, то Q-) / (-КД « К То-

1+Kj    1тп     К гда итоговую лог-линейную запись для функции спроса на деньги можно предста- вить в виде

~ а ~ ^mt = ^ ^C

~№>

где ц = ^;. Константу в уравнении спроса на деньги можно принять равной 1/ф с тем, чтобы уравнение выполнялось в усло- виях равновесия.

Таким образом, линеаризация условий первого порядка относительно равно- весного состояния дает следующую систему уравнений:

^C t = ^E[^C t+i ] ⁺ ~ ^(E[ ^ t+i ^{] — R} t ^{— 1п} Р ^);

а mt=^Ct — vRt;

1Lt=-(wt — aCt).

Можно отметить, что динамика переменных-отклонений не зависит от параметров функции полезности Ф и Ф. Кроме того, потребление оказывается независи- мым от денежного спроса и предложения труда, а они оба зависят от потребления, но не друг от друга.

Для моделирования реального сектора сформулируем модель ценообразования на рынках несовершенной конкуренции и зададим производственную функцию.

Наибольшее распространение, в том числе по причине простоты, получили модели негибких цен [8]. Мы будем следовать популярной модели ценообразования G. Calvo [9] и J. Rotemberg [10]. В работе [6] описан вывод уравнения новокейнсианской кривой Филлипса (NKPC) n_t = к • mcr_t + pE[n_t+1], где к - параметр Кальво, отражающий инерционность цен, а mcr_t - отклонение от равновесного значения для реальных предельных издержек.

В этой простой модели не выделены явные внешнеэкономические связи. Однако, согласно J. Gali [11], спецификация NKPC для открытой экономики не отличается от полученной авторами. Отличаются только сами откалиброванные коэффициенты, что непринципиально для статистического оценивания, которое будет проведено ниже.

Рассмотрим выражение для предельных издержек:

d(WL) _ dWL dL     _W + ^

MC =

dY     dL dY dL dL

dY dL

■

В условиях несовершенной конкуренции на рынке труда ставка заработной платы не фиксирована для фирм. Тогда обозначим эластичность заработной платы по труду через e ^L и, задав производственную функцию в виде функции Кобба – Дугласа Y = AL^a , получим предельные издержки:

W(1 + eL) MC=       L , aY/L а реальные предельные издержки –

W (1 + e L ) ^mcr = T^Y7T-

В логарифмах выражение для реальных предельных издержек принимает вид mcr = w — y + l + \n (----— ), a J где w - логарифм реальной заработной платы.

А с учетом производственной функции

— a t +in(i+^ w\ a C ^a J

mcr = w +

1 — ct

a

У

где a_t = lnA _t .

Лог-линейное приближение для ре- альных предельных издержек, записанное через отклонение от равновесных значений: mcrt = wt — Yt + lt или с учетом производственной функции и уравнения для реальных заработных плат:

,—    /1-а-ю         1-ю mcrt = (—;-+a)Yt——At ■

Как видим, без учета изменений в совокупной факторной производительно- сти реальные предельные издержки пропорциональны разрыву выпуска, что и используется зачастую для записи NKPC.

В литературе часто используется гибридная NKPC¹, предложенная J. Gali и M. Gertler [12] на основе эконометрических исследований:

Щ = к^ mcr_t + PE[n_t +i] + p_nn_t -! .

Для того чтобы равновесная инфляция совпадала с целевым уровнем, необходимо выполнить условие 1 = 0 + p_n .

Относительно гибридной модификации можно заметить, что наши предыдущие эконометрические исследования [13], а также исследования Национального банка Казахстана [14] указывают на инерционность инфляционных процессов.

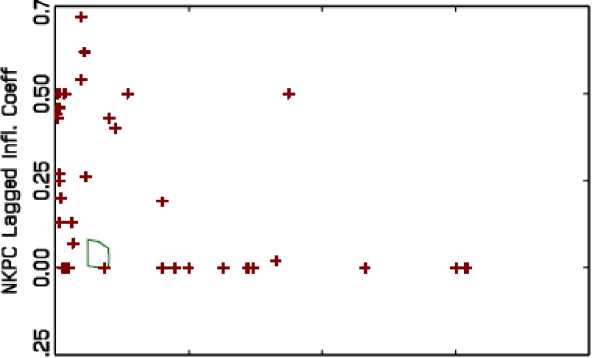
Поскольку, как было показано выше, подходов к спецификации NKPC, так же, как и подходов к оцениванию ее параметров, существует большое множество, то в литературе можно встретить большой разброс статистических оценок. Например, для экономики США в исследовании [15] приводится обзор таких оценок (рис. 1).

1Л

? 0.00      0.25        0.50        0.75        1.00

NKPC Marg. Cost Coeff

Рис. 1. Разброс оценок параметров NKPC в различных исследованиях по экономике США [15]

Национальные банки при разработке денежно-кредитной политики придерживаются правила Тейлора1[16]:

R t — ^ t = Y + Q n&t — n^{T )} + q_yY t .

1 Кроме того, можно указать еще одну спецификацию. В исследовании J. Gali и M. Gertler [12] высказали воз- ражения против перехода от реальных предельных издержек к разрыву выпуска. Однако, поскольку предельные издержки являются ненаблюдаемой перемен- ной, J. Gali и M. Gertler предложили использовать до-

W <±

__dY

лю труда в ВВП MCR

P

W 1

P dY dL

W 1  _ WL _ s

P aY/L ~ aPY ~ a'

Правило Тейлора указывает, что реальная, т. е. за вычетом инфляции, базовая ставка должна расти при превышении инфляцией своего целевого значения и при положительном разрыве выпуска. При этом центральные банки руководствуются принципом Тейлора: для стабилизации экономики реакция ставки процента на отклонение инфляции от таргета должна быть больше 1 (q_n > 1).

Константа у выбирается таким образом, чтобы в равновесном состоянии

(n_t = п^т и Y_t = 0) соблюдалось уравнение IS. Тогда у = —p.

Поскольку ставка процента не может изменяться слишком часто и резко в ответ на изменения экономической конъюнктуры, центральные банки используют сглаживание:

R_t-n_t = Y + q^ t - ^ ^T ) + q y Y t +

^{+ p}R^Rt-1 -

В этом случае у = p_R(n — p) — p.

Итоговая система состоит из следующих уравнений.

Уравнение для разрыва выпуска:

^r t = E[Y t ₊₁]+-(E[n_t+1] — R_t — p).

Функция спроса на деньги: ~ a mt = ^--Wt-

Предложение труда:

L t = fa - aY t ).

Новокейнсианская кривая Филлипса:

n_t = K- mcr_t + 0E\n_t+1] + p^ t-! .

Реальные предельные издержки: mcr = w_t-Y_t + L t -

Производственная функция:

Y = A t + al_t.

Уравнение Тейлора для процентной ставки:

R_t-n_t = Y + 4 n⁽ⁿt - ^^{T )} + q y Y t +

⁺ p R^Rt-1 -

Для практического использования построенной модели ее параметры должны быть откалиброваны и/или оценены. Поскольку для байесовского оценивания должны быть заданы параметры априорных распределений, мы используем оба подхода: откалиброванные значения параметров используются для задания параметров априорных распределений.

Калибрация параметров модели

П ри калибрации параметров модели мы будем следовать работе [17] .

В исследовании [14, с. 25] норма дисконтирования P была оценена эконо-метрически на уровне 0,438 для продовольственных товаров и 0,375 – для непродовольственных, и эти значения кажутся слишком низкими. Заниженные оценки могут являться эффектом, отмеченным в работе [18]: при оценивании «гибридного» NKPC лаговые переменные инфляции «вытесняют» будущие (leads), т. е. коэффициенты при ожиданиях оказываются заниженными или статистически незначимыми.

Более адекватные оценки были получены в диссертации Ж.Ш. Ишуовой [2] – 0,97. Б. Мухаметдиев оценил параметр P на уровне 0,98 [3] .

Параметр P калибруется из следующих соображений. В равновесии уравнение Эйлера приобретает вид P (^г)=

(1W)         _п1+п

= 7---"7. То есть P = 7-

(1+R*)

Цель по инфляции в Казахстане установлена в коридоре 5–7% (1,2–1,7% в квартал) и фактическая инфляция близка к этому уровню (5,3% к концу 2018 г.). Базовая ставка составляет 9,25% (2,2% в квартал). Соответственно, параметр P мы откалибруем на уровне 0,99.

Тогда параметр p будет равен p = lnP ~ —0,01. Далее мы будем оценивать этот параметр независимо от P, чтобы различить норму дисконирования домашних хозяйств и предприятий реального сектора, как это было сделано ранее в [6] .

Параметр а, отражающий эластичность межвременного замещения потребления, ранее мы калибровали на уровне 1, однако апостериорная оценка оказывалась близка к 4 (разброс оценок составил от 0,86 до 5,93 при средней 1,22). Б. Мухаметдиев оценил параметр на уровне 0,95 [3] – 1 [4] (хотя функция полезности несколько отличалась от нашей). В целом в литературе параметр а часто задается на уровне 1 (см., например, [11] ).

Параметр ^, обратный эластичности предложения труда по реальной заработной плате, калибровался на уровне 2,5 [3] – 3 [4] . В работе [2, с. 95] оцененное значение 7,69 признается крайне завышенным и в итоге принимается на уровне 3 (оценки выше 3 в литературе по DSGE-моделям не встречается).

В исследовании [19] эластичность спроса на деньги (агрегат М3) по доходу оценена на уровне 2,82, по проценту – 0,041. Соответственно, мы зададим ^ = 1/3, ^ = 0,04.

„               (1-(J(1-/?()

Параметр к =---------зависит от доли фирм с инерционными ценами ш. Для США этот параметр калибруется на уровне 2/3 [11, с. 52], что означает, что в среднем цены остаются фиксированными на протяжении 3 кварталов (к = 0,17). Для Казахстана можно ожидать, что цены более гибки, по крайней мере в сторону повышения. Например, ш = 0,7 в [4] и к = 0,12 [3].

Ориентация на эконометрические оценки других авторов затрудняется тем, что в основном в качестве фактора NKPC используются не реальные предельные издержки, а разрыв выпуска: 0,159 и 0,651 для продовольственных и непродовольственных товаров соответственно [14, с. 25]; 0,336 в [2, с. 94]; 0,2278 в [6] .

Исходя из оценки ш = 0,7 и наших оценок Д = 0,99, мы установим параметр к = 0,132.

Ранее мы оценивали коэффициент инерционности инфляции р_п на уровне 0,06 (разброс от 0,03 до 0,15, среднее 0,09)

• [6]    или 0,25–0,30 [13] . В исследовании [14, с. 25] параметр был оценен в 0,162 и 0,243 для продовольственных и непродовольственных товаров соответственно. Мы выберем параметр р_п = 0,1.

Ранее мы оценивали эластичность выпуска по труду а на уровне 0,185 [6] .

В публикации сотрудников Национального банка Казахстана [5] содержится описание моделей, используемых для разработки процентной политики. На основе этой публикации мы определим p_R = 0,75, q_R = 2,5, q_n = 0,5. Цель по инфляции установлена Национальным банком Казахстана на уровне 7%, то есть п^т = 0,07/4.

Тогда константу в уравнении Тейлора зададим как у = p_R(u^T — р} — р = 0,027 .

Для калибрации коэффициентов автокорреляции шоков мы оценим модели вида e_t = pe_t-1 + e_t , где e_t - случайные возмущения соответствующих переменных. Стандартная ошибка уравнения использовалась для калибрации среднеквадратического отклонения случайных возмущений (табл. 1).

Таблица 1

Параметры авторегрессионных моделей случайных шоков

Переменная	Автокорреляция случайных возмущений	Стандартные ошибки случайных возмущений
V	0,737	0,020
m-t	0,821	0,049
L t	0,445	0,007
^ t	0,130	0,016
R t	0,857	0,003

Для¹расчета процентных отклонений (для переменных ВВП, численность наемных рабочих, дефлированная денежная масса М2, реальная заработная плата) вначале проводилось устранение сезонности с помощью процедуры Census в пакете EViews 7.0 . Затем рассчитывалось сглаженное значение фильтром Ходрика – Прескотта в пакете EViews 7.0 (стандартный параметр для квартальных данных Л = 1600).

Наконец, рассчитывалось процентное отклонение z_sat

Zt = ln—^, L                  *   ,

^Zt где Z_t - процентное отклонение для переменной z_t ; z_sa_t - значение переменной z_t после устранения сезонности; z t - значение переменной z_t, сглаженное фильтром Ходрика – Прескотта.

Далее, используя байесовский подход, оценим откалиброванные значения параметров DSGE-модели экономики Казахстана.

Оценка параметров модели

Байесовское оценивание пришло на смену традиционному эконометрическому оценива- нию и калибрации параметров. Подход получает все большее распространение при оценивании параметров VAR- и DSGE-моделей [20–23]. Его особенностью являет- ся то, что при оценивании параметров используются не только статистические данные, но и априорные суждения. Априорная информация о значении параметров может быть получена из положений экономической науки, экспертных суждений, результатов предыдущих исследований. Использование априорных знаний позволяет компенсировать нехватку статистических данных на коротких временных рядах.

Априорные знания задаются в виде функций распределения f(0) неизвестных параметров 0. Далее на основе имеющихся наблюдений y по формуле Байеса рассчитывается функция апостериорного распре- f(ymv f(y)

f(0\y) =

к L(y\0)f(0),

где f(y) - функция плотности распределе ния наблюдений; f(0) - функция априорного распределение параметров; f(y\0) = = L(y\0) - функция правдоподобия.

Таким образом, еще одной особен- ностью байесовского оценивания является использование функций распределения. Для получения точечных оценок рассчи- тывают математическое ожидание, медиа- ну или моду апостериорного распределения f(0\y)

В качестве априорных распределений принято использовать следующие функции (рис. 2):

– для положительных параметров моделей – гамма-распределение, для остальных – нормальное распределение (реже – равномерное);

– для авторегрессионных коэффициентов, которые принимают значения от 0 до 1, – бета-распределение;

деления:

– для среднеквадратических отклонений – обратное гамма-распределение.

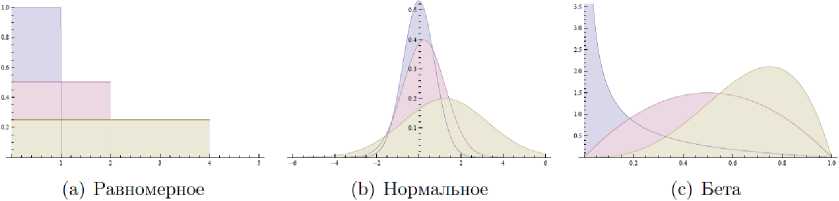
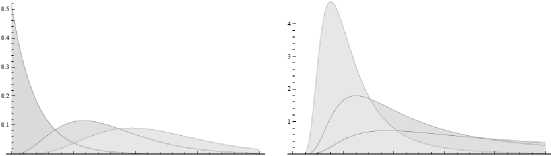
(d) Гамма                (е) Обратное гамма

Рис. 2. Вид функций распределения в байесовском оценивании при различных значениях их параметров [24, с. 38]

Учитывая эти рекомендации, нам остается задать средние значения априорных распределений параметров на основе откалиброванных выше значений. Априорные значения дисперсии задаются обычно максимально возможными, чтобы не сужать диапазон оценивания.

Оценивание проводилось с помощью пакета Dynare на квартальных данных Комитета по статистике Казахстана с 2000 по 2017 гг. (данные по индексу реальной заработной платы – с 2004 г., табл. 2).

Таблица 2

Параметры DSGE-модели экономики Казахстана и параметры их распределений

Параметр	Распределение	Априорное среднее	Априорное стандартное отклонение	Апостериорное среднее
p	Гамма	0,99	0,009	0,9867
p	Гамма	0,01	0,009	0,0027
a	Гамма	1	0,9	0,1817
p	Гамма	3	2,9	12,0935
Ф	Гамма	1/3	0,3	0,6242
и	Гамма	0,04	0,03	0,0369
к	Гамма	0,132	0,13	1,4638
pn	Бета	0,1	0,09	0,0246
Q n	Гамма	2,5	1	2,5009
Q y	Гамма	0,5	0,2	0,1343
P r	Бета	0,75	0,1	0,7828
Y	Нормальное	0,027	1	-0,0283
a	Гамма	0,185	0,18	0,0801
P y	Бета	0,737	0,2	0,8874
pm	Бета	0,821	0,1	0,8664
P l	Бета	0,445	0,2	0,6223
pp	Бета	0,130	0,1	0,363
pr	Бета	0,857	0,1	0,1158
P a	Бета	0,7	0,3	0,8089
a	Обр.гамма	0,020	Inf	0,0212
am	Обр.гамма	0,049	Inf	0,0191
a	Обр.гамма	0,007	Inf	0,0461
ap	Обр.гамма	0,016	Inf	0,0051
ar	Обр.гамма	0,003	Inf	0,0467

Ниже представлены графики априорных и апостериорных распределений для ключевых оцениваемых параметров (рис. 3).

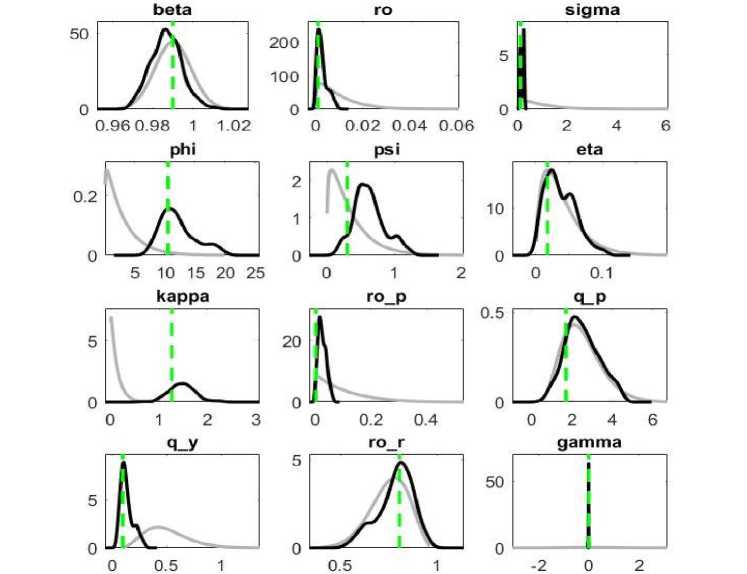
Рис. 3. Графики априорных (серый цвет) и апостериорных (черный) функций плотности распределения параметров DSGE-модели экономики Казахстана

При анализе полученных результатов обращают на себя внимание следующие моменты. Параметр и, отражающий межвременное замещение потребления, оказался значительно меньше 1.

Наоборот, оценка параметра ^ оказалась очень высокой, что говорит о низкой эластичности предложения труда к заработной плате. Аналогично, очень высокие оценки параметра к (параметр отрицательно связан с долей фирм, не корректирующих цены) могут свидетельствовать о высокой инерционности инфляционных процессов. Оба результата говорят об институциональном несовершенстве рынков труда и товаров в Казахстане (результаты, ожидаемые для всего постсоветского пространства).

Оценки параметров правила Тейлора в целом подтверждают, что Национальный банк Казахстана в своей монетарной политике ориентируется на стабилизацию инфляции, практически не обращая внимания на стабилизацию выпуска.

Параметр рр, учитывающий инерционность ценовых шоков, оказался гораздо выше значений, откалиброванных нами. И, наоборот, коэффициент рг, отражаю- щий инерционность шоков процентной ставки, оказывается близким к 0.

Далее проведем сценарные расчеты на основе оцененных параметров.

Численные эксперименты и анализ результатов

О ценим, как повлияют на эндогенные переменные, выраженные через отклонения от равновесных значений, шоки спроса, процентной ставки, цен и предложения труда. Все шоки по величине равны одному среднеквадратическому отклонению, оцененному выше для случайных возмущений. Расчеты проведены на 16 периодах, что соответствует 4 годам реального времени.

При росте совокупного спроса (рис. 4) ускоряется инфляция, и, следуя принципу Тейлора, Национальный банк повышает базовую ставку. Сдерживающая процентная политика снижает эффект от первоначального импульса совокупного спроса. Рост спроса на деньги вследствие роста дохода перевешивается снижением в результате роста процентной ставки. На рынке труда рост экономической активности вызывает повышение реальной заработной платы и предложения труда.

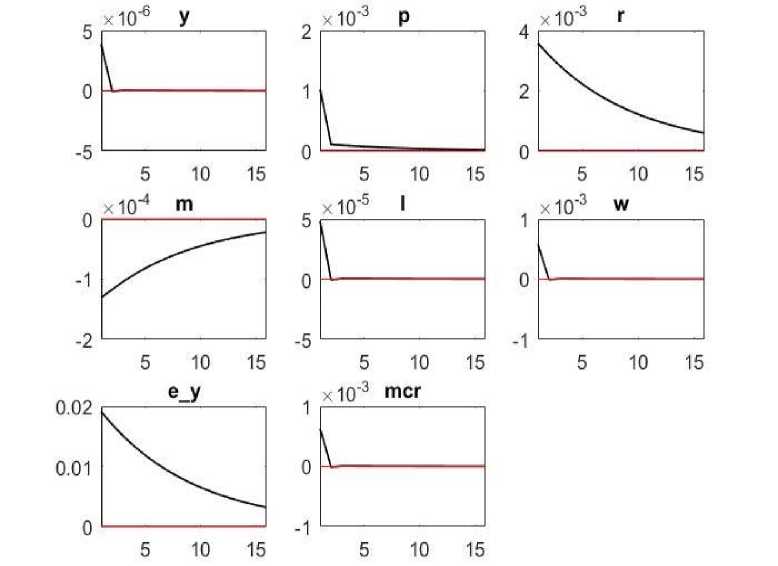
Рис. 4. Функции отклика при шоке спроса в DSGE-модели экономики Казахстана

Рост процентной ставки (рис. 5) приводит к отрицательному разрыву выпуска и снижению инфляции. Однако далее снижение инфляции ниже целевого уровня, установленного Национальным банком, приводит к необходимости сни- жения ставки процента, что увеличивает спрос на деньги. Снижение экономической активности населения отражается на рынке труда в снижении заработной платы и уровня занятости.

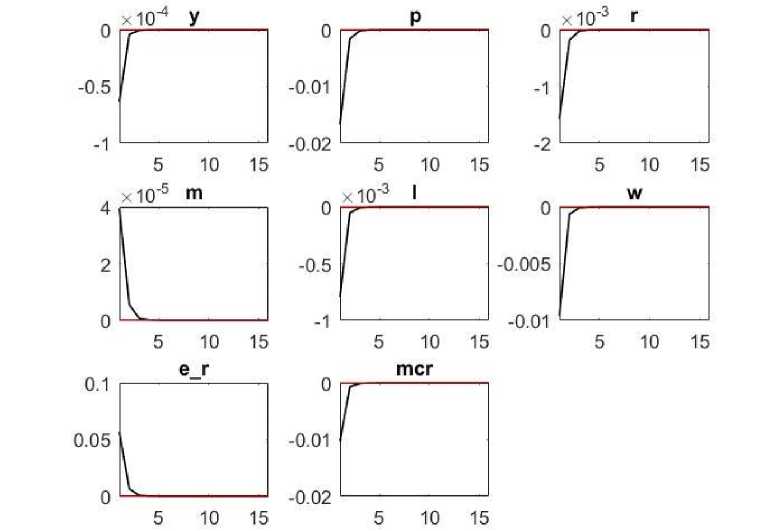
Рис. 5. Функции отклика при шоке процентной ставки в DSGE-модели экономики Казахстана

Экзогенный рост цен (рис. 6) заставляет денежный регулятор повысить базовую ставку, чтобы сдержать инфля- ют снижение выпуска ниже равновесного уровня, снижение спроса на деньги, уровня занятости населения и уровня заработной цию. Рост цен и ставки процента вызыва-      платы.

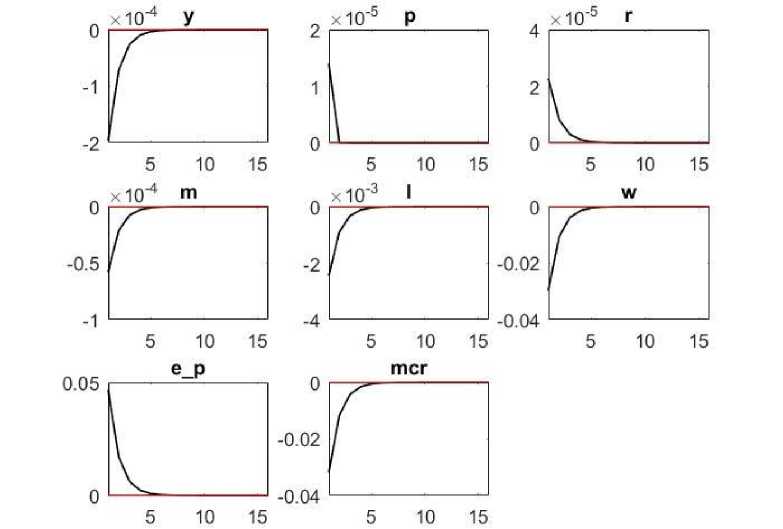
Рис. 6. Функции отклика при ценовом шоке в DSGE-модели экономики Казахстана

При росте предложения труда (рис. 7), что может быть вызвано выходом на рынок новых кадров, или притоком мигрантов, или изменением пенсионного возраста, снижается реальная заработная пла- ня, что вынуждает Национальный банк Казахстана снизить процентную ставку. Последнее увеличивает совокупный спрос (рост уровня занятости напрямую увеличивает экономическую активность населе- ния) и спрос на деньги.

та. Через реальные предельные издержки инфляция опускается ниже целевого уров-

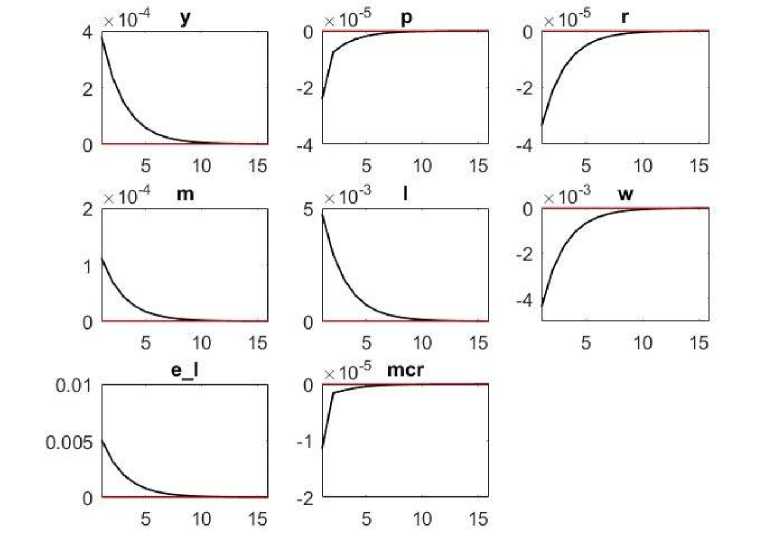
Рис. 7 . Функции отклика при шоке предложения труда в DSGE-модели экономики Казахстана

Таким образом, разработанная DSGE-модель экономики Казахстана позволяет анализировать эффекты от изменений монетарной политики и оптимизации ее параметров.

Заключение

Описана малая DSGE-модель экономики Казахстана. Модель описывает поведение домашних хозяйств и предприятий реального сектора в условиях несовершенной конкуренции и негибких цен. Для сектора домашних хозяйств выведены уравнения потребления, спроса на деньги и предложения труда. Реальный сектор описывается с помощью производственной функции, уравнения реальных предельных издержек и кривой Филлипса. Замыкает систему уравнение Тейлора, описывающее про-

Для оценивания параметров модели используется байесовский подход. Полученные оценки позволили сделать вывод о слабой чувствительности предложения труда к уровню заработной платы и об очень высокой инерционности инфляционных процессов. Последнее значительно усложняет антиинфляционную политику Национального банка Казахстана.

В дальнейшем модель может быть развита за счет учета таких средне- и долгосрочных факторов, как инвестиции в основной капитал и динамика основных фондов, фискальная политика государства. Добавление в модель параметров внешней торговли и мировой экономики позволит использовать построенную модель в качестве составного блока для модели Таможенного союза.

центную политику денежного регулятора в условиях инфляционного таргетирования.